基于复杂网络的不同路由策略下交通流驱动的流行病传播
张永强,李爽,马金龙
(河北科技大学信息科学与工程学院,石家庄 050018)
流行病伴随着人类社会的发展,如SARS、中东呼吸综合征等尤其新型冠状肺炎,超过200个国家和地区先后出现疫情,表现出大流行特征[1]。由此可见流行病严重地威胁着人类的生命与安全,给人类社会造成了极大的危害。
大多数经典的流行病传播模型都未考虑交通流的驱动,假设如下:在每一个时间步,每个节点的传染性与该节点的度成正比[2],即被感染的节点会以相等的概率将流行病传播到其所有邻居节点。然而,对于真实的网络,交通流是影响流行病传播的重要因素。例如,在全球航空网络中,如果人们没有在城市之间进行相关的旅行活动,流行病就不可能在不同的地理区域之间传播[3]。在社交网络中,如果没有蚊虫叮咬,典型的登革热流行病就不会在人群中传播[4]。在上述传播过程中,网络中节点的传染性与节点度没有直接关系,而与交通流有关。这种耦合的传播过程被称为基于交通流的流行病传播[5]。近年来,复杂网络理论和路由算法被广泛应用于交通运输网络[6-7]上和节点的能耗问题[8-9]中,而针对交通流驱动的流行病传播动力学的研究相对较少。
Meloni等[10]提出了基于交通流的易感-感染-易感(susceptible-infected-susceptible,SIS)流行病传播模型,发现流行病阈值不再取决于节点的度,而是直接取决于交通流。王亚奇等[11]在基于交通流的易感-感染(susceptible-infected,SI)流行病传播模型上提出了一种改进的熟人免疫机理,结果表明:对网络实施目标免疫能够有效抑制流行病的传播。Yang等[12-13]观察到可以通过本地路由策略和有效路由协议策略控制流行病的传播。Yang等[14-15]提出了一种通过去除网络中部分边来控制基于交通流的流行病传播的方法,并研究了幂律度分布对基于交通流的流行病传播的影响。郑国庆等[16]在两层星型网络上建立了一个新的有效度流行病模型,研究发现切断边界与中心的传播途径以及免疫中心节点对降低发病率最有效。Chen等[17]在交通流驱动的流行病传播上研究了异质感染率的影响,发现当感染率与节点度呈负相关时,可以有效地抑制流行病的蔓延。Jing等[18]研究了交通流分配策略对多层网络中流行病传播的影响,发现通过调整某一层的路由分配和增加某一层的平均连通性都可以有效地抑制流行病的传播。多重结构[19-21]对流行病传播的影响也开始受到关注。
研究表明,网络的结构特征[14,16,19-21]和交通流的路由策略[12-13,18]都会影响流行病的传播。其中,改变路由策略不需要对网络拓扑结构进行重构,相比于改变网络的结构特征成本较低、使用方便。鉴于此,研究不同的路由策略对基于交通流的流行病传播动力学的影响。
1 模型
1.1 网络模型
由于很多真实网络(如互联网、电话网络和运输网络)具有无标度特性[22],因此使用Barabási-Albert(BA)模型[23]来生成网络模型。BA无标度网络模型的生成算法步骤如下。
步骤1初始网络。给定m0个原始节点,m0个节点可以是孤立的,也可以是全连通的。
步骤2增长网络。每个时间步内都有一个具有m条边的新节点加入网络中,其中m≤m0。
步骤3连接规则。每个增加的新节点连接到已有节点w的概率与节点w的度成正比。
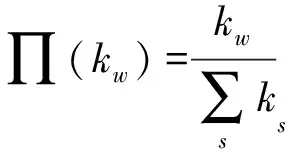
(1)
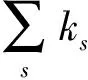
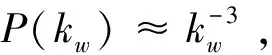

图1 BA无标度网络的演化过程
1.2 基于交通流的SI流行病传播模型
以SI模型[24]为研究对象,研究基于交通流的流行病传播过程。基于交通流的SI流行病传播模型与传统的SI流行病传播模型不同:节点被感染的概率不仅与流行病的传染率β有关,还与网络中的交通流量有关。在基于交通流的流行病传播模型中,数据包传输过程如下:在规模为N的网络中,每个时间步产生λN个新数据包,它们随机选择源节点和目的节点。数据包存储在节点队列中,队列采用先进先出(first-in-first-out)的原则,节点接受和转发数据包的能力不受限制。数据包按照既定的路由策略进行传输,一旦到达目的节点,就会从网络中移除。当易感节点收到来自感染节点的数据包时,该节点被感染的概率为β。最初,通常假设一部分节点受到感染。图2描述了基于交通流的SI流行病传播模型的传播过程。
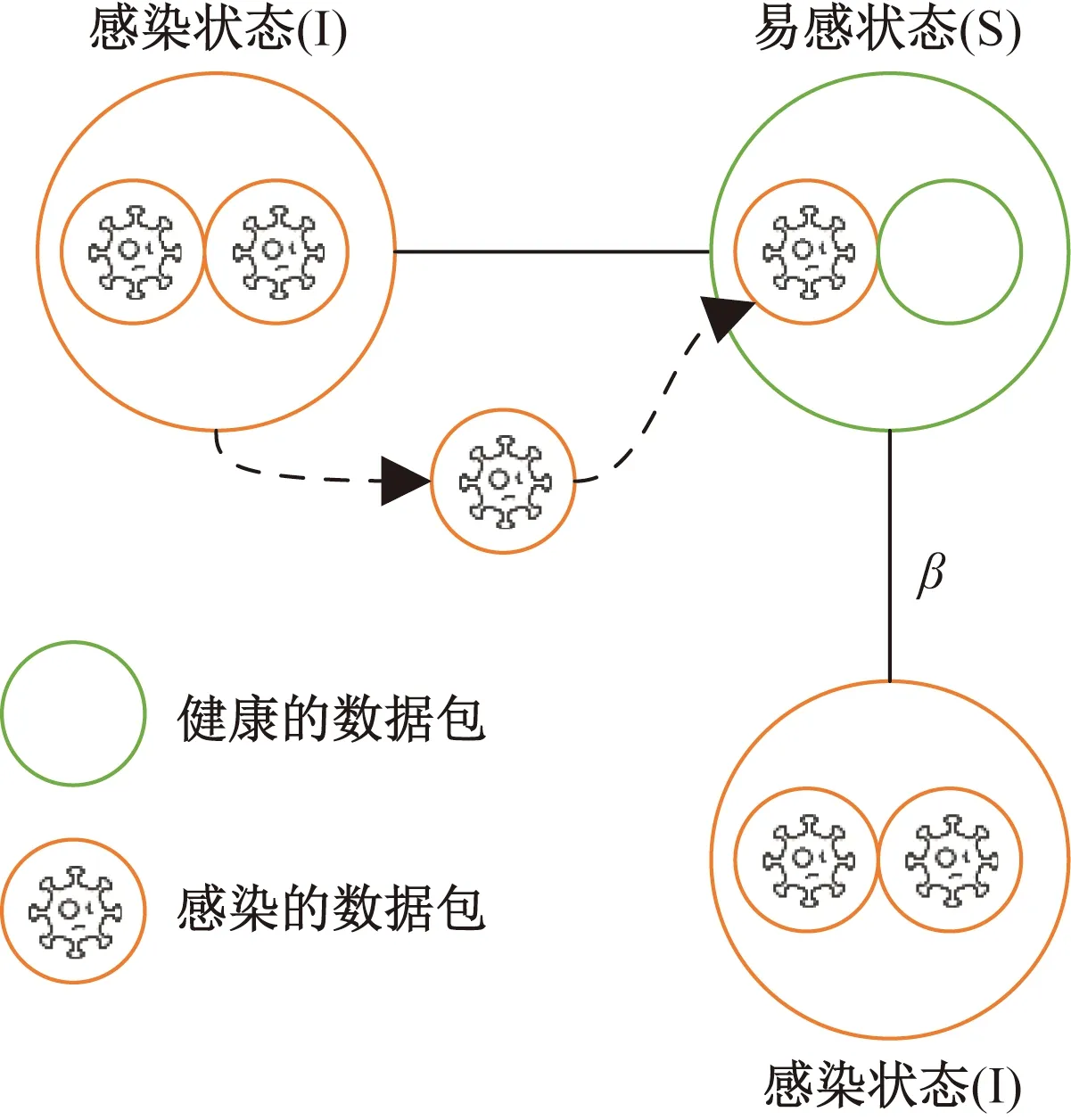
图2 基于交通流的SI流行病传播模型的传播过程
由于无标度网络中每个节点的度并不相同,因此度为v的节点组中被感染节点的密度为ρv(t)=Iv(t)/Nv。其中,Nv是度为v的节点数量,Iv(t)是t时刻度为v的被感染节点数量。根据平均场理论[25],得出基于交通流的SI流行病传播模型的反应速率方程为[26]
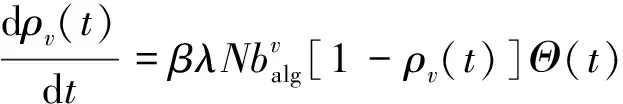
(2)
在不考虑节点之间的度相关性和约定P(v)为节点度分布函数的情况下,Θ(t)的表达式为
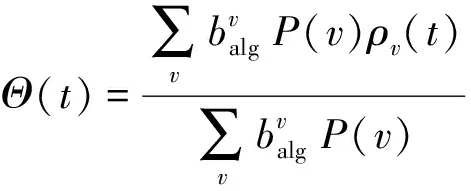
(3)
在初始传播阶段,感染节点所占比例较小,因此可以忽略感染节点密度(ρ)平方项的时间复杂度O(ρ2),将式(2)简化为
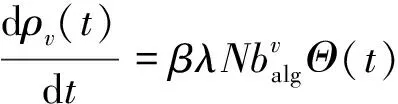
(4)
将式(3)代入式(4)得
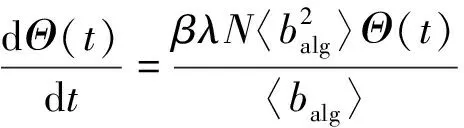
(5)
由式(5)可得
Θ(t)=Θ(0)e1/τ
(6)
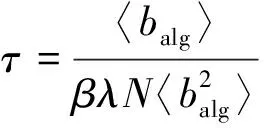
(7)
式(7)中:τ为流行病爆发的时间尺度。
由式(7)可知,τ与传染率β和每个时间步生成的数据包数目λN成反比。
2 策略分析与仿真
分析3种路由策略对基于交通流的流行病传播动力学的影响,路由策略包括内容如下。
(1)有效路径(efficient path, EP)路由策略[27]。研究发现网络中度值大的节点容易成为拥塞的瓶颈节点,所以将网络中节点的度值作为路由选择的代价函数。例如,从节点i到节点j的路径为P(i→j):=i≡x1,x2,…,xn≡j,其代价函数为
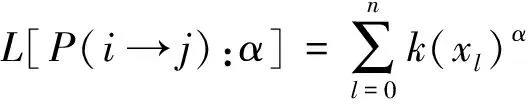
(8)
式(8)中:k(xl)为节点xl的度;α为可调参数,α=1是EP路由策略的最优参数值。
(2)最短路径(shortest path,SP)路由策略[28]。数据包选择多条路径中边数最少的那一条路径作为传输路径。当式(8)中的α=0时,EP路由策略恢复为SP路由策略。
(3)概率路径(probability path,PP)路由策略[29]。为了能够更加有效的发挥中心节点传输数据包的能力,减少数据包在路由路径上等待时间的概率,提出了PP路由策略,可表示为
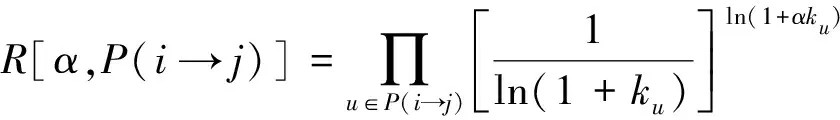
(9)
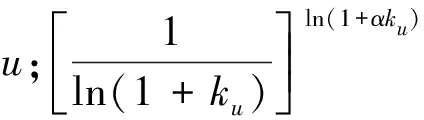
使路由函数R[α,P(i→j)]取得最大值的路径就是概率路由路径P*(i→j)。
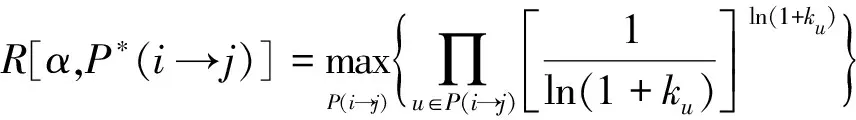
(10)
然后,在BA无标度网络上对不同路由策略下基于交通流的SI流行病传播模型进行仿真实验。设定BA网络的平均度为
图3(a)、图4(a)和图5(a)分别展示了在N=400、1 200、2 000的网络规模中,SP路由策略下感染节点密度ρ(t)与数据包生成率λ的对应关系。图3(b)、图4(b)和图5(b)分别展示了在N=400、1 200、2 000的网络规模中,PP路由策略下感染节点密度ρ(t)与数据包生成率λ的对应关系。图3(c)、图4(c)和图5(c)分别展示了在N=400、1 200、2 000的网络规模中,EP路由策略下感染节点密度ρ(t)与数据包生成率λ的对应关系。其中传染率β=0.1。从图3~图5中可以看出,在这3种路由策略下,不同的网络规模中,感染节点的密度ρ(t)都随着数据包生成率λ的增加而增加。这是因为当网络中传输的数据包数量增加时,就会把流行病传播给更多的节点,这显然与传统的SI流行病传播模型不同。该仿真结果证明了式(7)中的结论:在确定β和N的情况下,流行病的传播随着λ的增加而变快。因此,在流行病爆发时控制交通流量可以有效地提高流行病的爆发阈值,抑制流行病的传播。
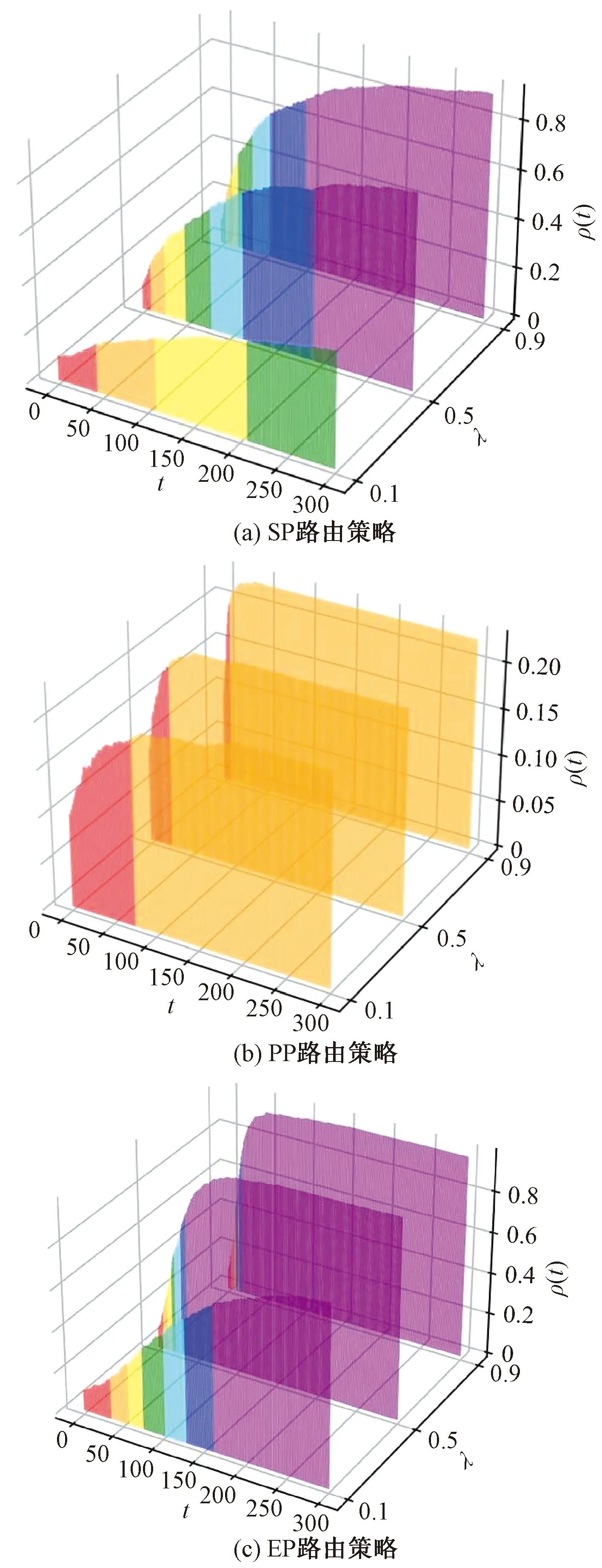
表示感染节点密度的范围是[0, 0.2);表示感染节点密度的范围是[0.2, 0.3);表示感染节点密度的范围是[0.3, 0.4);表示感染节点密度的范围是[0.4, 0.5);表示感染节点密度的范围是[0.5, 0.6);表示感染节点密度的范围是[0.6, 0.7);表示感染节点密度的范围是[0.7, 1]
表示感染节点密度的范围是[0, 0.2);表示感染节点密度的范围是[0.2, 0.3);表示感染节点密度的范围是[0.3, 0.4);表示感染节点密度的范围是[0.4, 0.5);表示感染节点密度的范围是[0.5, 0.6);表示感染节点密度的范围是[0.6, 0.7);表示感染节点密度的范围是[0.7, 1]
表示感染节点密度的范围是[0, 0.2);表示感染节点密度的范围是[0.2, 0.3);表示感染节点密度的范围是[0.3, 0.4);表示感染节点密度的范围是[0.4, 0.5);表示感染节点密度的范围是[0.5, 0.6);表示感染节点密度的范围是[0.6, 0.7);表示感染节点密度的范围是[0.7, 1]
图6(a)、图7(a)和图8(a)分别展示了在N=400、1 200、2 000的网络规模中,SP路由策略下感染节点密度ρ(t)与传染率β的对应关系。图6(b)、图7(b)和图8(b)分别展示了在N=400、1 200、2 000的网络规模中,PP路由策略下感染节点密度ρ(t)与传染率β的对应关系。图6(c)、图7(c)和图8(c)分别展示了在N=400、1 200、2 000的网络规模中,EP路由策略下感染节点密度ρ(t)与传染率β的对应关系。其中数据包生成率λ=0.1。从图6~图8中可以看出,在这3种路由策略下,不同的网络规模中,感染节点的密度ρ(t)都随着传染率β的增加而增加。这说明流行病传播不仅与交通流有关,还与流行病自身固有属性有关。因此,在制定有关流行病传播的防控策略时,要进行综合考虑。该仿真结果验证了式(7)中的结论:在确定λ和N的情况下,β的增加会导致流行病的传播阈值降低。
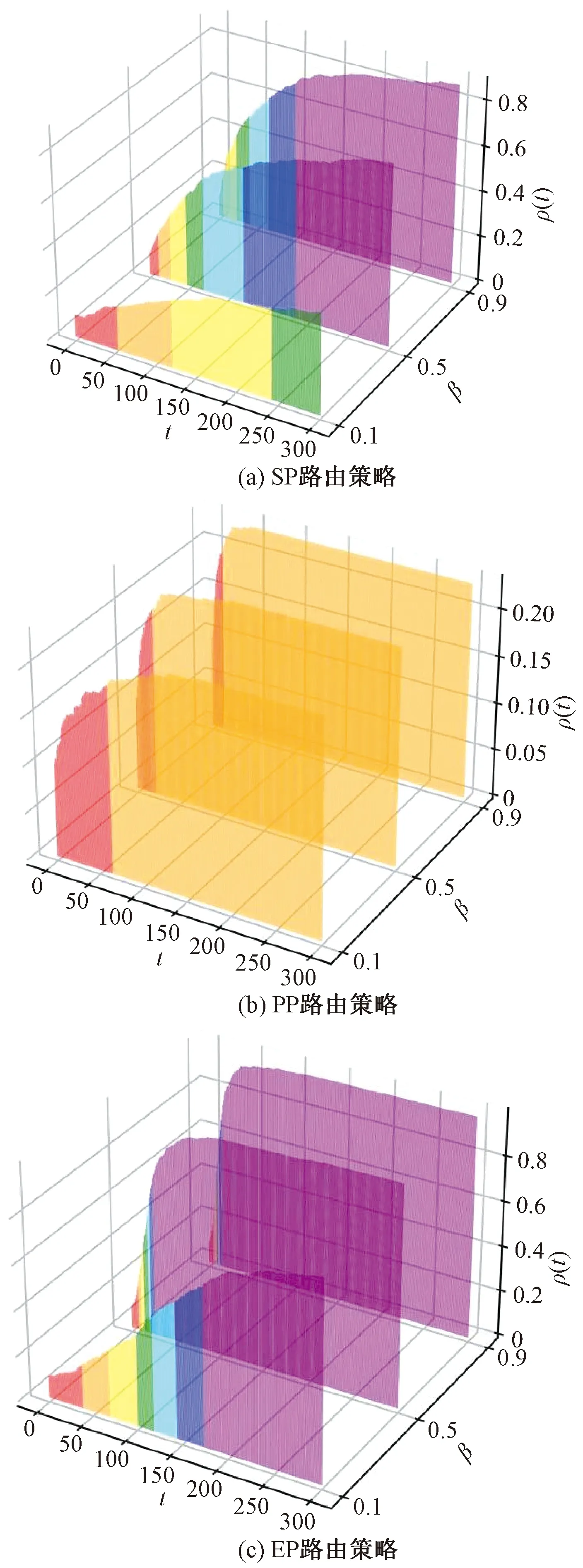
表示感染节点密度的范围是[0, 0.2);表示感染节点密度的范围是[0.2, 0.3);表示感染节点密度的范围是[0.3, 0.4);表示感染节点密度的范围是[0.4, 0.5);表示感染节点密度的范围是[0.5, 0.6);表示感染节点密度的范围是[0.6, 0.7);表示感染节点密度的范围是[0.7, 1]
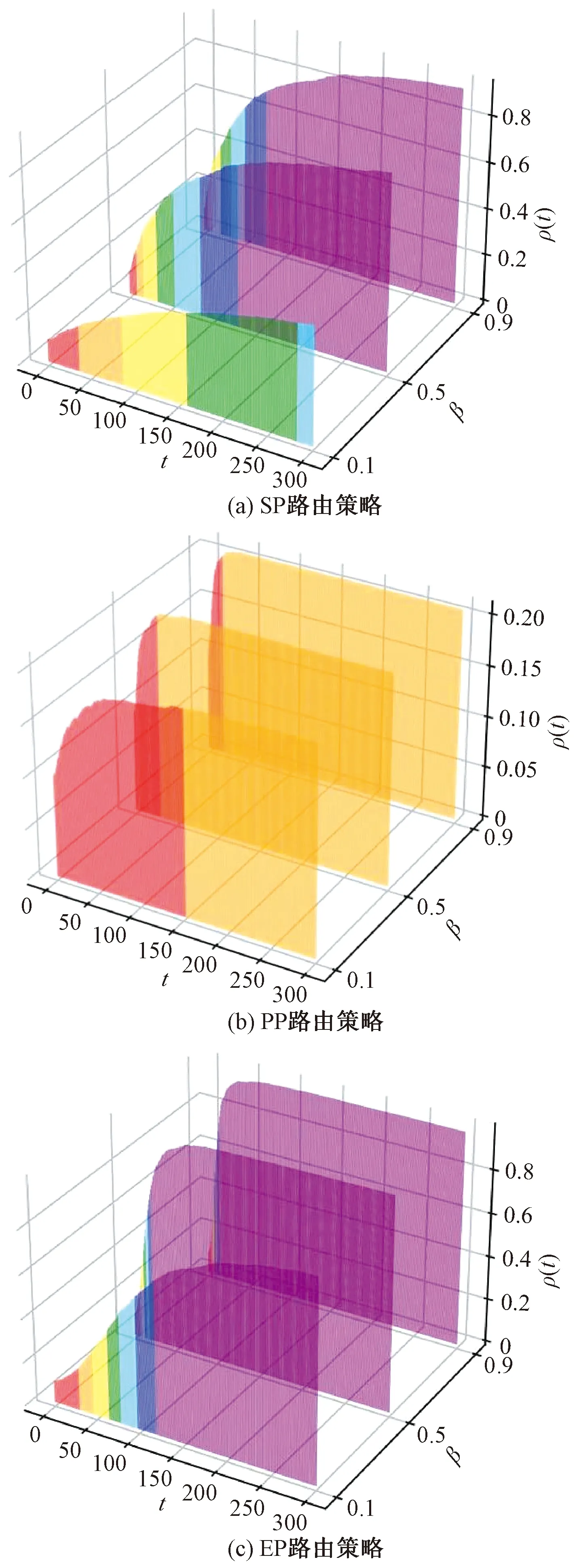
表示感染节点密度的范围是[0, 0.2);表示感染节点密度的范围是[0.2, 0.3);表示感染节点密度的范围是[0.3, 0.4);表示感染节点密度的范围是[0.4, 0.5);表示感染节点密度的范围是[0.5, 0.6);表示感染节点密度的范围是[0.6, 0.7);表示感染节点密度的范围是[0.7, 1]
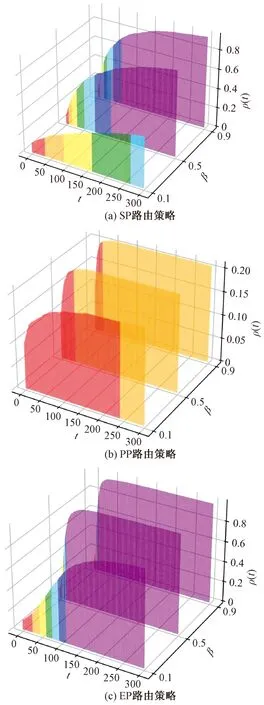
表示感染节点密度的范围是[0, 0.2);表示感染节点密度的范围是[0.2, 0.3);表示感染节点密度的范围是[0.3, 0.4);表示感染节点密度的范围是[0.4, 0.5);表示感染节点密度的范围是[0.5, 0.6);表示感染节点密度的范围是[0.6, 0.7);表示感染节点密度的范围是[0.7, 1]
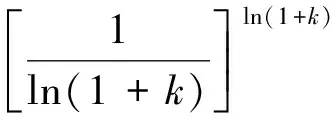
图9的仿真实验结果(以N=1 200的网络规模为例)证明了上述结论,可以看出,在SP路由策略、PP路由策略和EP路由策略中,EP路由策略下被感染的数据包在节点上的分布最均匀,即交通范围更广。而PP路由策略下被感染的数据包在节点上的分布最集中,即交通范围更小。所以得出结论:相比于SP路由策略,PP路由策略会抑制流行病的传播,而EP路由策略会加速流行病的传播。
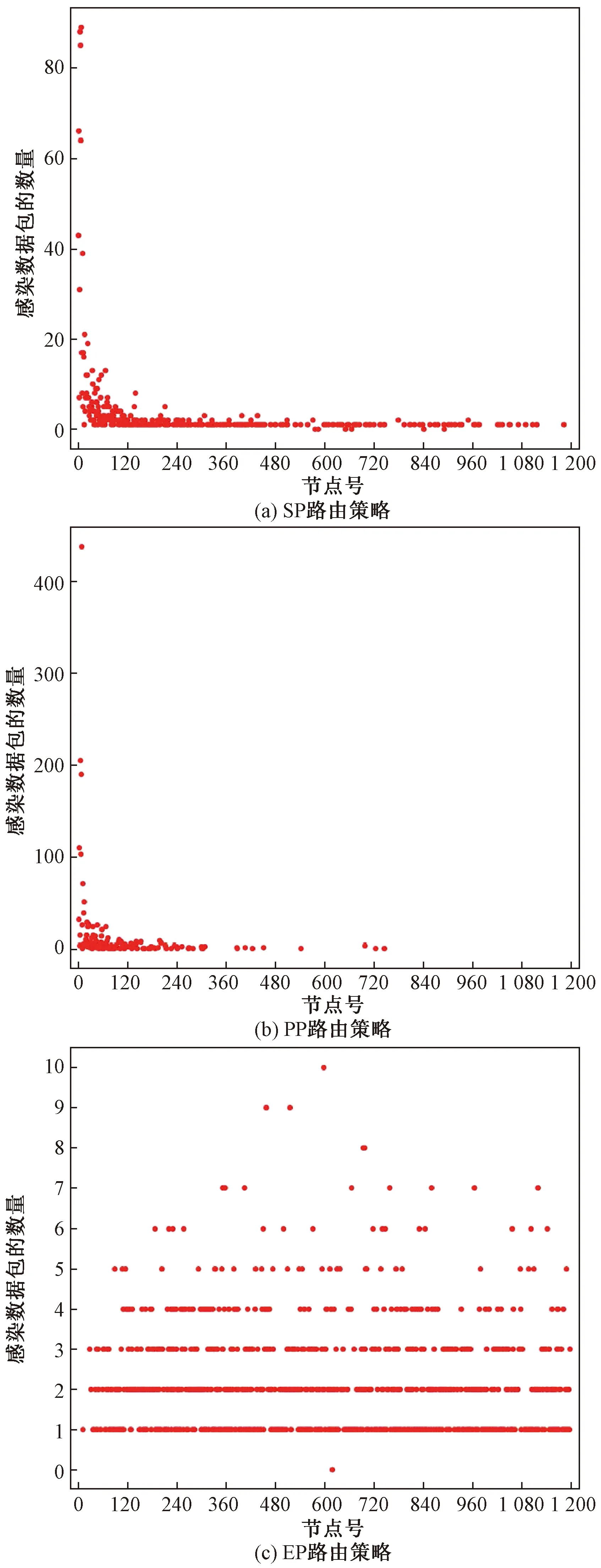
图9 不同路由策略下被感染的数据包在节点上的分布情况
3 结论
基于交通流的流行病传播与其数据包进行传输时采用的路由策略密切相关。研究了3种路由策略对基于交通流的流行病传播的影响,发现相比于SP路由策略,PP路由策略可以有效地抑制流行病的传播,而EP路由策略则会加速流行病的传播,仿真结果在不同的网络规模上具有鲁棒性。除此之外,还发现在不同的路由策略下,减少交通流量和降低传染率可以有效地抑制流行病的传播。因此,当流行病爆发时,在交通流和传染率一定的情况下,可以通过调整路由策略来抑制流行病的传播。这些研究结果对在突发公共卫生事件下,交通管理部门有针对性地制定防控策略,保障基本民生,稳定经济运行具有一定指导意义。

