内贴CFRP加固圆形隧洞弧形界面力学性能研究

施钟淇，秦 敢，杨 帆

内贴CFRP加固圆形隧洞弧形界面力学性能研究

施钟淇1, 2, 3，秦 敢2, 3，杨 帆1

(1. 合肥工业大学土木与水利工程学院，合肥 230009；2. 深圳市城市公共安全技术研究院有限公司，深圳 518038；3. 城市安全风险监测预警应急管理部重点实验室，深圳 518038)

内贴碳纤维增强复合材料(CFRP)加固圆形隧洞时，弧形加固界面的力学性能是影响CFRP与衬砌混凝土两种材料能够变形协调共同承载的重要因素．考虑弧形加固界面的黏结滑移，建立了界面应力理论分析模型，分析了界面曲率变化对界面应力状态的影响；通过建立CFRP加固圆形隧洞数值分析模型，着重研究了胶层的弹性模量和厚度、CFRP的弹性模量和厚度、CFRP的粘贴层数等加固参数变化时，弧形加固界面应力状态的变化规律；最后结合具体工程案例，在兼顾隧洞衬砌满足加固条件的同时，从减小界面应力、防止结构出现剥离破坏的角度对上述参数的选择提出优化方案．计算分析与工程案例研究结果表明：界面曲率的存在使得加固界面上不仅存在环向应力，而且会存在径向应力，界面应力状态相比于加固界面为平面而言更为复杂；界面曲率的变化对界面环向应力无明显影响，但对界面径向应力影响显著，随着界面曲率半径的逐渐降低，界面径向应力水平会显著提高；选择弹性模量较小的胶层，适当减小胶层的涂刷厚度，可以显著降低弧形加固界面的应力水平，从而降低结构发生剥离破坏的潜在风险；在满足结构受力与承载要求的前提条件下，建议选择厚度较薄、弹性模量较小的碳纤维材料对圆形隧洞进行加固，同时尽可能地减少粘贴层数，对CFRP与衬砌混凝土的长期共同作用有利．

隧洞加固；弧形界面；界面应力；黏结滑移；有限元分析

中国有大量的隧洞已运行数十年，受到设计、施工、运行和管理等多方面因素的影响，相当数量的隧洞存在不同程度的老化和病害问题，如混凝土碳化、衬砌开裂等．这些病害会导致隧洞结构的稳定程度降低，严重时会危及整个工程的安全．因此，对已建隧洞的病害及其相应整治措施的研究已经引起国内外学者的普遍重视．由于碳纤维增强复合材料(carbon fiber reinforced polymer，CFRP)具有强度高、性能稳定、耐腐蚀、自重轻等特点[1]，内贴CFRP加固技术在运输的便捷性、施工质量控制、施工效率以及后期维护等方面相较于黏钢加固技术而言也具有明显的优势，在隧洞结构补强中具有广泛的应用前景[2]．

采用CFRP加固混凝土时，主要通过加固界面传递的界面应力使CFRP参与承载．因而，CFRP-混凝土界面的力学性能是研究者所关心的核心问题．国内外针对CFRP-混凝土界面黏结-滑移本构模型[3-5]、界面应力的计算方法[6-8]等方面开展了大量卓有成效的研究，积累了宝贵的研究经验和丰富的研究成果．然而上述研究多是针对以下结构而展开：①各类梁、板结构的抗弯或抗剪加固；②各类柱、墩结构的抗压加固或者抗震加固．采用内贴CFRP补强圆形隧洞时，加固界面为内凹的弧形曲面，与梁、板、柱、墩结构的界面形式存在明显的区别．因此，上述研究成果并不能直接用于CFRP补强圆形隧洞弧形界面的力学性能分析．

此外，针对CFRP加固拱桥或曲面砌体结构，加固界面也为弧形曲面，与内贴CFRP加固圆形隧洞的界面形式具有一定的相似性．相关学者对其弧形界面黏结-滑移关系[8-10]、界面应力的解析计算模型[11-13]以及界面剥离破坏机理[14-15]进行了较为系统的研究．但相比于拱桥和曲面砌体结构而言，隧洞的工作环境、结构形式、荷载特点等复杂程度更高，上述研究成果对内贴CFRP补强圆形隧洞的加固方案设计与施工的指导作用也十分有限．

因此，本文采用理论推导与有限元计算相结合的方法，针对CFRP补强圆形隧洞弧形加固界面的界面应力分布规律以及界面应力集中问题展开深入探讨．首先，基于CFRP、胶层和衬砌混凝土相互作用计算模型，考虑弧形加固界面的黏结滑移，推导了弧形加固界面的应力解析表达式，分析了界面曲率变化对界面剥离破坏的影响，确定了影响弧形加固界面应力状态的关键参数．然后，建立了能够考虑弧形加固界面黏结滑移和胶层局部剪切压缩特性的三维有限元模型，并结合内贴CFRP加固圆形隧洞模型试验(后文简称“模型试验”)[2]的实测结果验证了有限元模型的有效性．基于该有限元模型，分析了关键参数的变化对弧形界面复杂应力状态的影响规律，以期为内贴CFRP加固圆形隧洞的施工方案设计提供指导．

1 界面应力理论解析

1.1 弧形加固界面应力理论分析模型

弧形加固界面型式对比如图1所示．

按照CFRP加固圆形隧洞的结构特点，设计了如图2(a)所示的基本力学模型．模型中CFRP的厚度为c，弹性模量为c，黏结长度为；胶层的厚度为a，胶层的弹性模量为a，界面曲率半径为，施加的荷载值为，加载方向为加载点的切线方向．提取该微元段建立理论分析模型，如图2(b)所示．

图1 加固界面型式对比

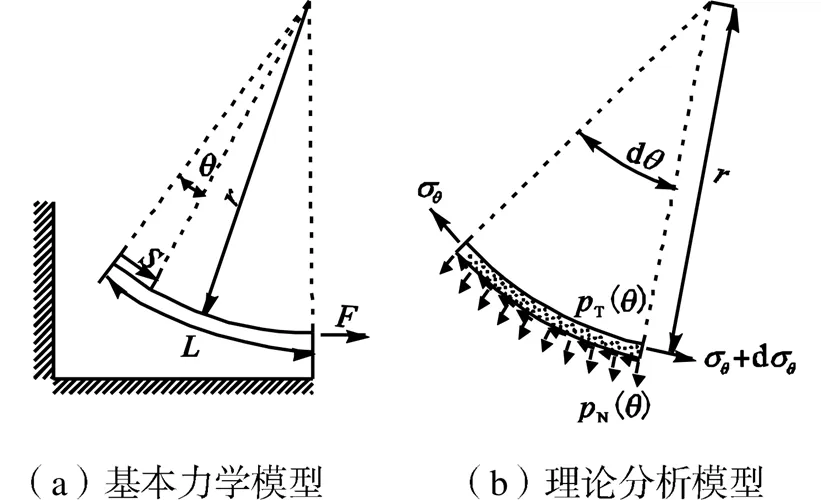
图2 弧形加固界面应力理论分析模型

为简化计算，将CFRP和胶层简化为一层加固材料[16]，其等效的厚度为

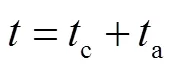
其等效的弹性模量为

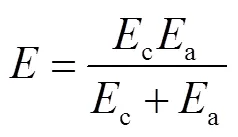
加固材料的环向应力为σ，加固界面径向应力和切向应力分别为N和T．

如图2(b)所示，微元段的平衡方程为

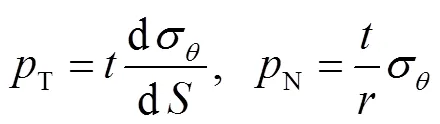
根据胡克定律，加固材料的应力应变关系为

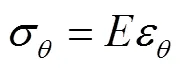
将式(4)代入式(3)中，有

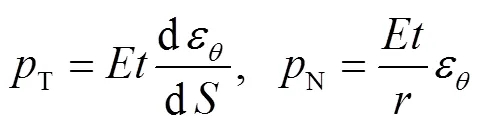
胶层和混凝土界面的相对滑移量T和N可定义为

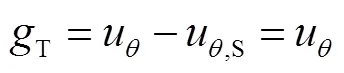
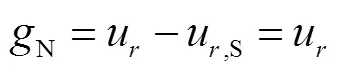
相对于胶层的变形，混凝土的变形往往很小，故在推导过程中将加固界面混凝土的径向位移和切向位移忽略[17]．界面应力和界面滑移量的关系为

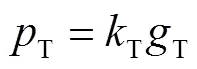
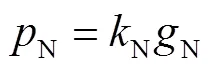
式中：T为界面切向刚度；N为界面径向刚度．将式(8)和(9)代入式(5)，有

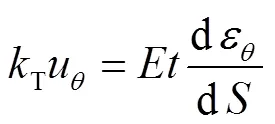
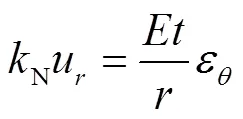
极坐标下的几何方程为

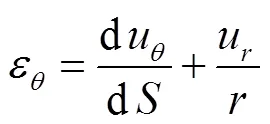
将式(12)代入式(10)和(11)，有

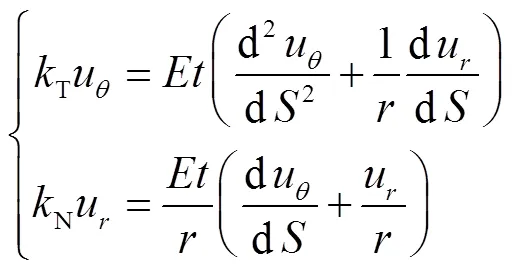
则

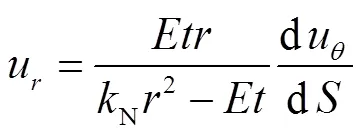
将式(14)代入式(13)，有

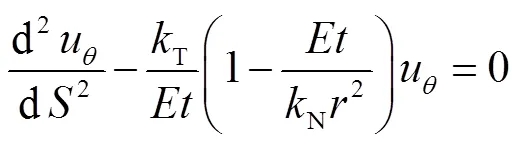
定义变量

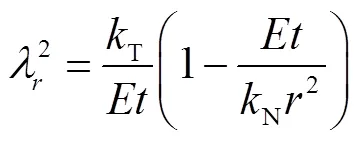
将式(16)代入式(15)中，有

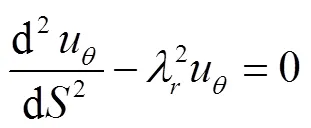
求解式(17)，可得

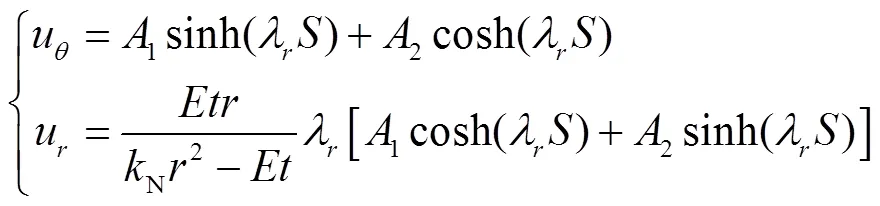
将式(18)代入式(11)，有

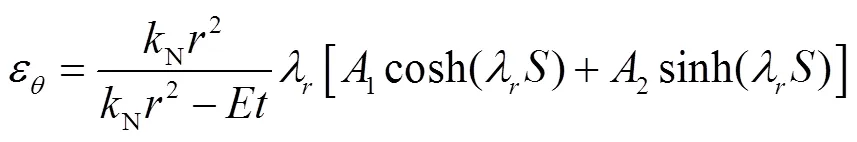
式中1和2为待定的常数，由边界条件决定．

对于如图2(a)所示的力学模型，其边界条件为

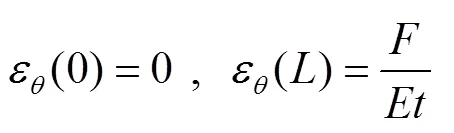
将式(20)代入式(19)中，可以求得

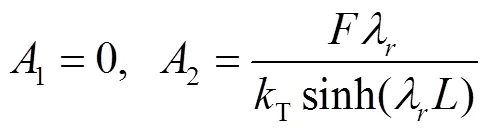
将式(21)代入式(18)中，有

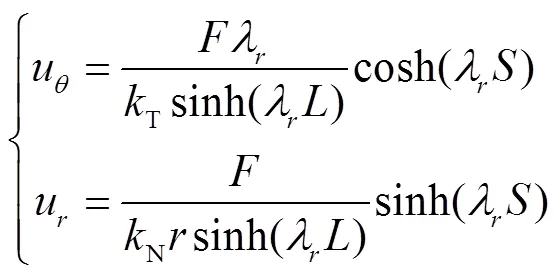
根据式(22)并结合式(8)和式(9)，界面径向应力和界面环向应力的表达式可表示为

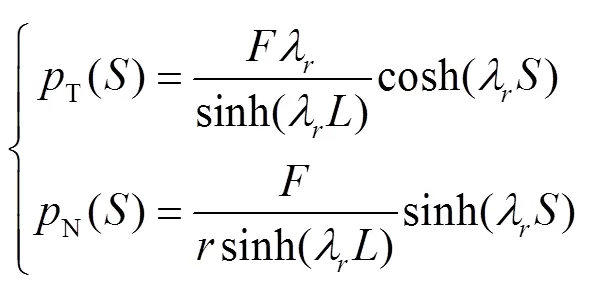
1.2 界面曲率对界面应力状态的影响

根据式(23)分析在不同界面曲率条件下弧形加固界面的应力变化规律．试件的各项参数与荷载如表1所示，界面应力的计算结果如图3所示．

表1 计算参数取值

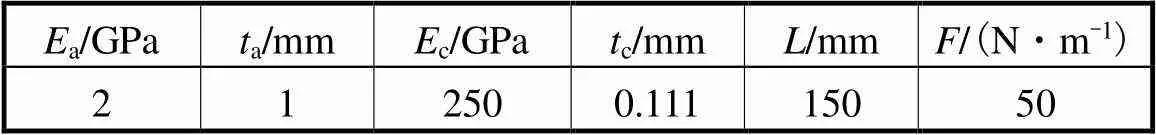
Tab.1 Values of calculation parameters

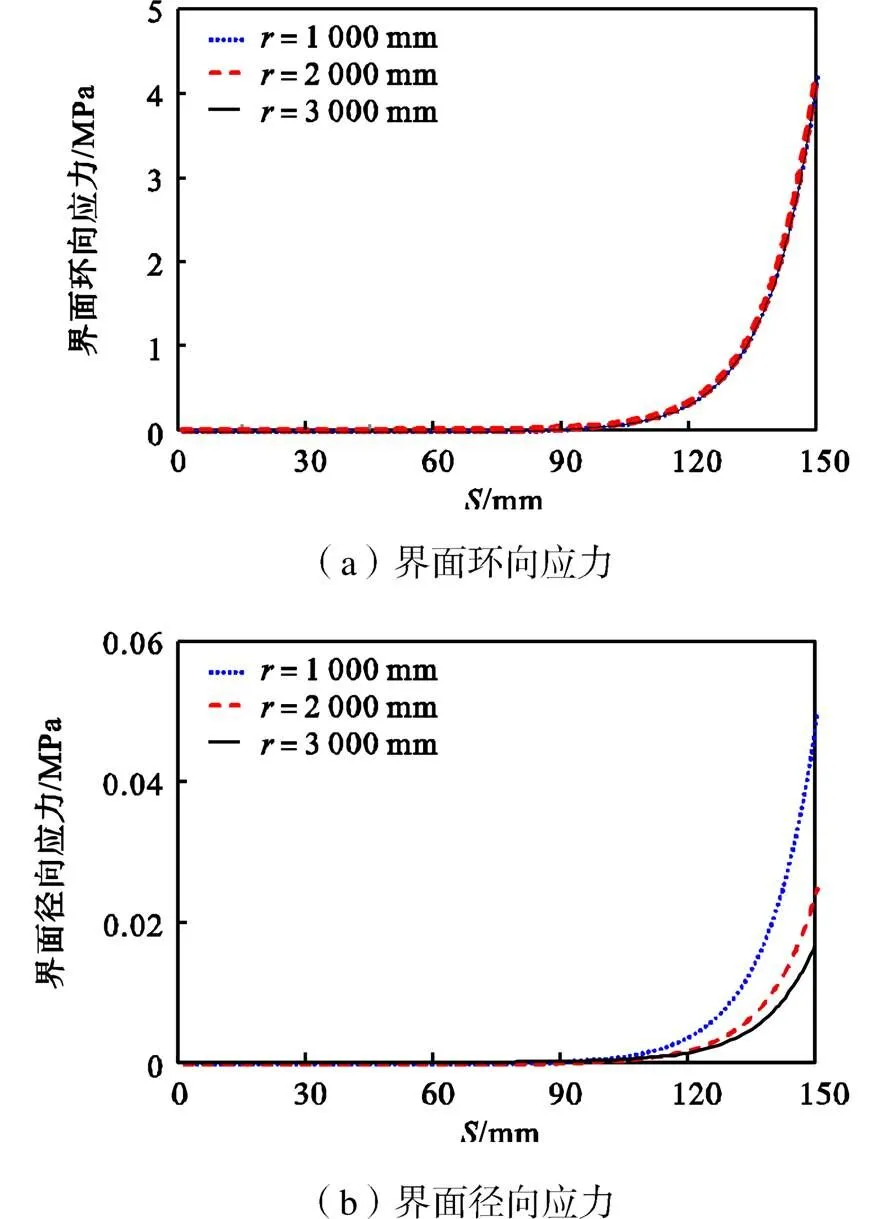
图3 界面应力计算结果

由图3(a)可知，在界面曲率发生变化时，界面环向应力的应力水平以及分布规律均不会发生改变．由图3(b)可知，对于加固界面为平面的情况，界面径向应力为零；随着界面曲率半径的逐渐降低，界面径向应力水平会呈明显增加的态势．

在混凝土梁或柱的CFRP抗弯加固和抗剪加固中，加固界面多为平面，加固界面主要处于纯剪状态．对于内贴CFRP补强圆形隧洞，加固界面为弧形曲面．理论计算结果表明，界面曲率的存在使得弧形加固界面上不仅存在界面环向应力，而且会存在界面径向应力．因而，相比于加固界面为平面而言，加固界面为曲面时的界面应力状态更为复杂．

1.3 复合应力状态对剥离破坏的影响

以界面保护层混凝土的主应力达到混凝土的抗拉强度为判断剥离的准则，故剥离应力的表达式为

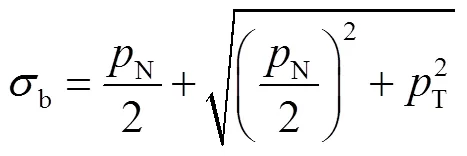
对于界面径向应力而言，应力值为正代表胶层和衬砌混凝土的弧形界面处于受拉状态，应力值为负代表胶层和衬砌混凝土的弧形界面处于受压状态．对于界面环向应力而言，应力值的正负表示弧形加固界面受剪的方向不同．采用CFRP加固圆形隧洞时，界面保护层混凝土一般处于两种状态：①界面保护层混凝土径向受压，环向受剪切．根据式(24)可以看出，此时界面是否发生剥离破坏主要受环向的剪切应力T控制，径向压应力N的存在对防止结构出现剥离破坏是有利的；②界面保护层混凝土径向受拉，环向受剪切．根据式(24)可以看出，此时属于最不利工况，径向拉应力的存在会进一步提高界面的应力水平，从而导致结构更早地出现剥离破坏．

为了降低界面径向受拉给结构带来不利影响，采取优化材料选择以及施工工艺措施的方法来降低界面径向拉应力的水平．结合式(23)可知，界面应力主要受到c、c、a、a以及加固层数等因素的影响．胶层种类繁多，不同种类的胶层固化后的弹性模量不同；胶层的厚度也受实际涂刷操作以及固化环境的影响而出现较大差别．对于CFRP材料，一般分为高强型和高弹模型等种类，不同种类的CFRP的厚度和弹性模量也有一定的差别．因此，在后续的分析中，需结合实际进一步探讨c、c、a、a以及加固层数的变化对弧形加固界面复合应力状态的影响．

2 界面应力参数优化分析

2.1 基本参数

采用有限元方法对上述参数的优化选择问题进行深入分析．参考模型试验[2]建立CFRP加固圆形隧洞三维有限元数值分析模型．试件的材料参数如表2所示．图4[2]给出了模型试验的加载方式和应变片布置的情况．

2.2 模型概况

有限元模型见图5．混凝土采用Solid65实体单元模拟，钢筋采用Link8杆单元模拟，采用Solid45实体单元模拟胶层，采用Shell63壳单元模拟CFRP，CFRP和胶层均简化为线弹性材料．采用三向弹簧单元(Combin39)模拟胶层和衬砌混凝土加固界面的黏结滑移行为，弹簧刚度的计算方法参考文献[18]．

表2 材料参数

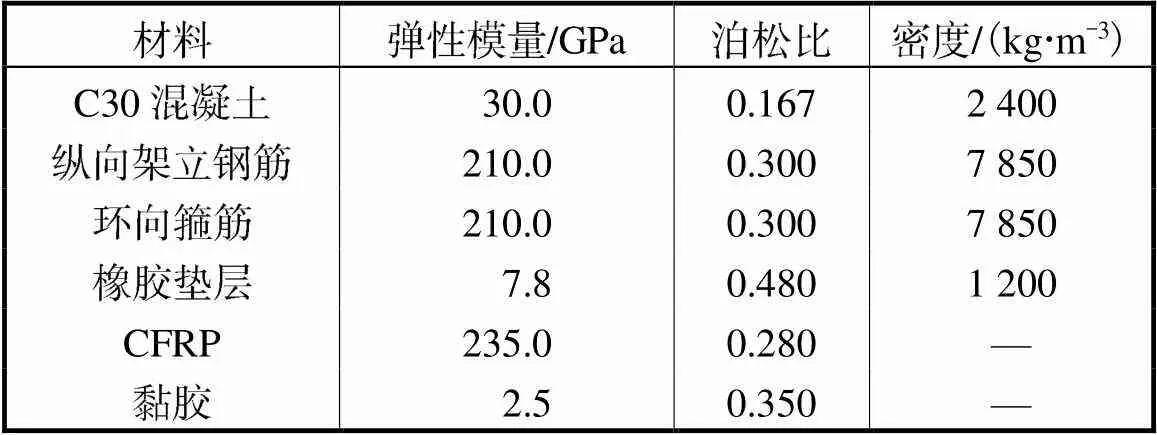
Tab.2 Material parameters

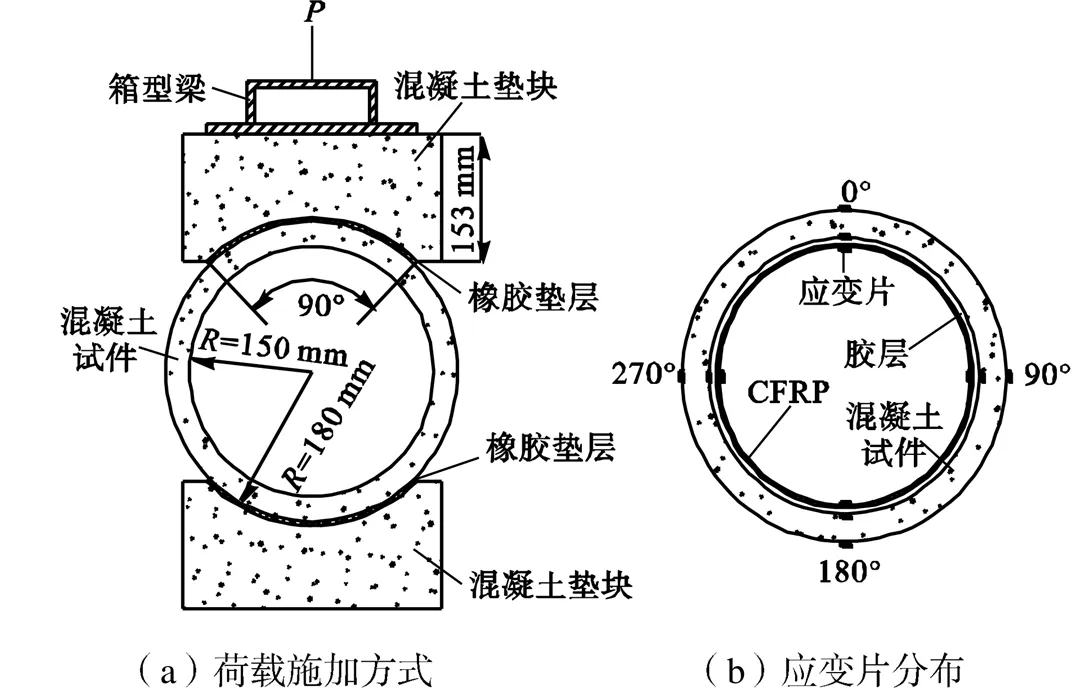
图4 模型试验示意

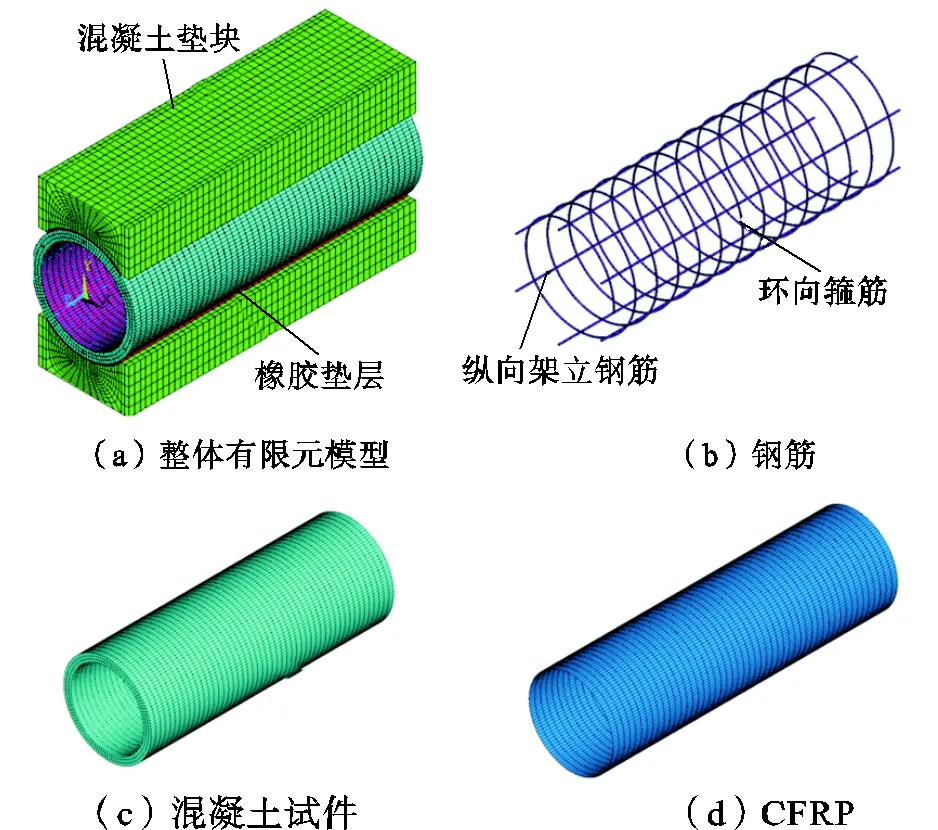
图5 有限元模型

2.3 计算结果对比验证

为验证上述三维有限元模型的有效性，对模型试验进行非线性有限元分析，并将计算得出的混凝土试件内外表面以及CFRP上的应变变化规律同试验实测结果进行对比．试件90°处的混凝土内表面环向微应变以及CFRP环向微应变的对比如图6所示．

由图6可见，在20kN的垂直荷载作用下，计算得出的混凝土微应变和实测微应变的差别仅为5.3%.由于将胶层和CFRP简化为线弹性材料，故CFRP的计算微应变和实测值差别较大，但计算值和实测值的最大差别在13.6%之内．总体上，数值计算结果和模型试验结果吻合较好．

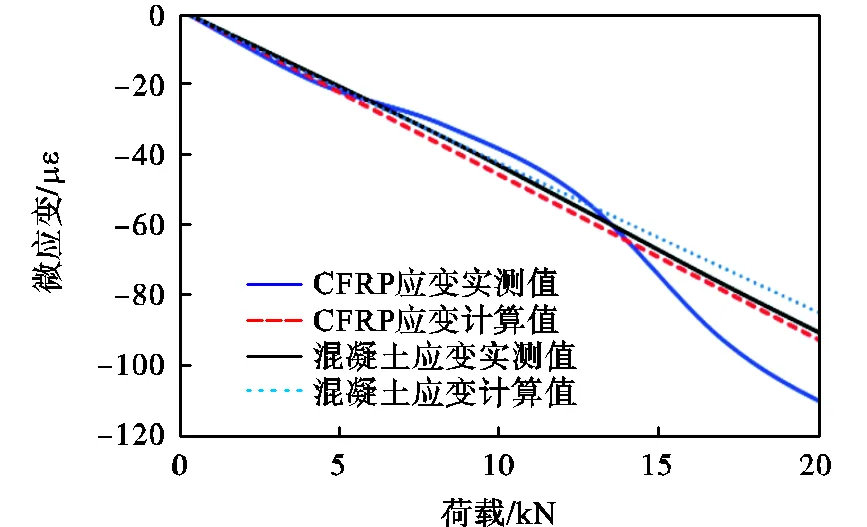
图6 数值结果和试验结果对比

2.4 界面应力参数分析

采用单因素分析方法研究a、a、c、c以及粘贴层数变化时，界面应力的变化规律，即每次分析只变动1个变量，而其他影响因素保持基本取值不变，参数的基本取值参照模型试验．参考大多数工程实践，计算考虑的参数变化范围如表3所示．如图4[2](b)所示，以试件拱顶为0°，顺时针方向展开呈现加固界面径向应力和环向应力的分布情况．

表3 参数取值

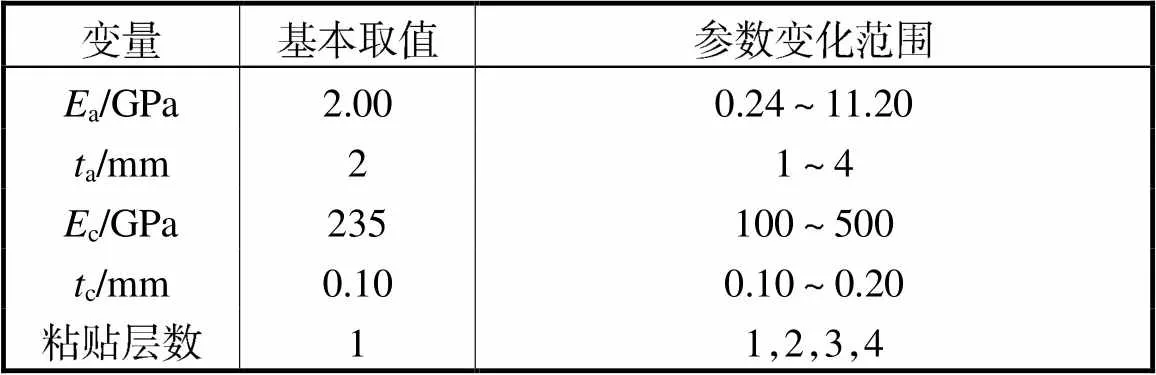
Tab.3 Parameter values

2.4.1 粘贴层数对界面应力的影响

从图7可以看出，随着粘贴层数的增加，界面径向应力和环向应力的分布规律没有发生明显变化，界面径向受拉区的范围也没有明显扩大，但界面径向最大拉应力和环向最大应力均出现了大幅度的增长.当粘贴层数由1层逐渐增加到4层的过程中，界面最大径向拉应力由0.013MPa逐渐增加到0.044MPa，增加幅度约为238%；界面最大环向应力由0.068MPa逐渐增加到0.172MPa，增加幅度约为153%.粘贴层数过多，不仅会增大界面应力，还会增加黏结胶浸入CFRP的难度．因此，在满足结构受力的前提条件下，建议尽可能地减少粘贴层数．

2.4.2a对界面应力的影响

从图8可以看出，受拉区径向应力和环向应力的大小均随着a的增加而明显增大．当胶层厚度由1mm逐渐增加到4mm的过程中，界面最大径向拉应力的增加幅度为45.5%；界面最大环向应力的增加幅度为27.4%．因此，在胶层的涂刷过程中，适当地减小胶层的涂刷厚度有利于改善界面的应力集中程度，从而降低结构出现剥离破坏的风险．而且，过厚的胶层在固化过程中将产生较大的收缩而导致CFRP无法有效黏结，不利于CFRP与衬砌混凝土长期联合承载．

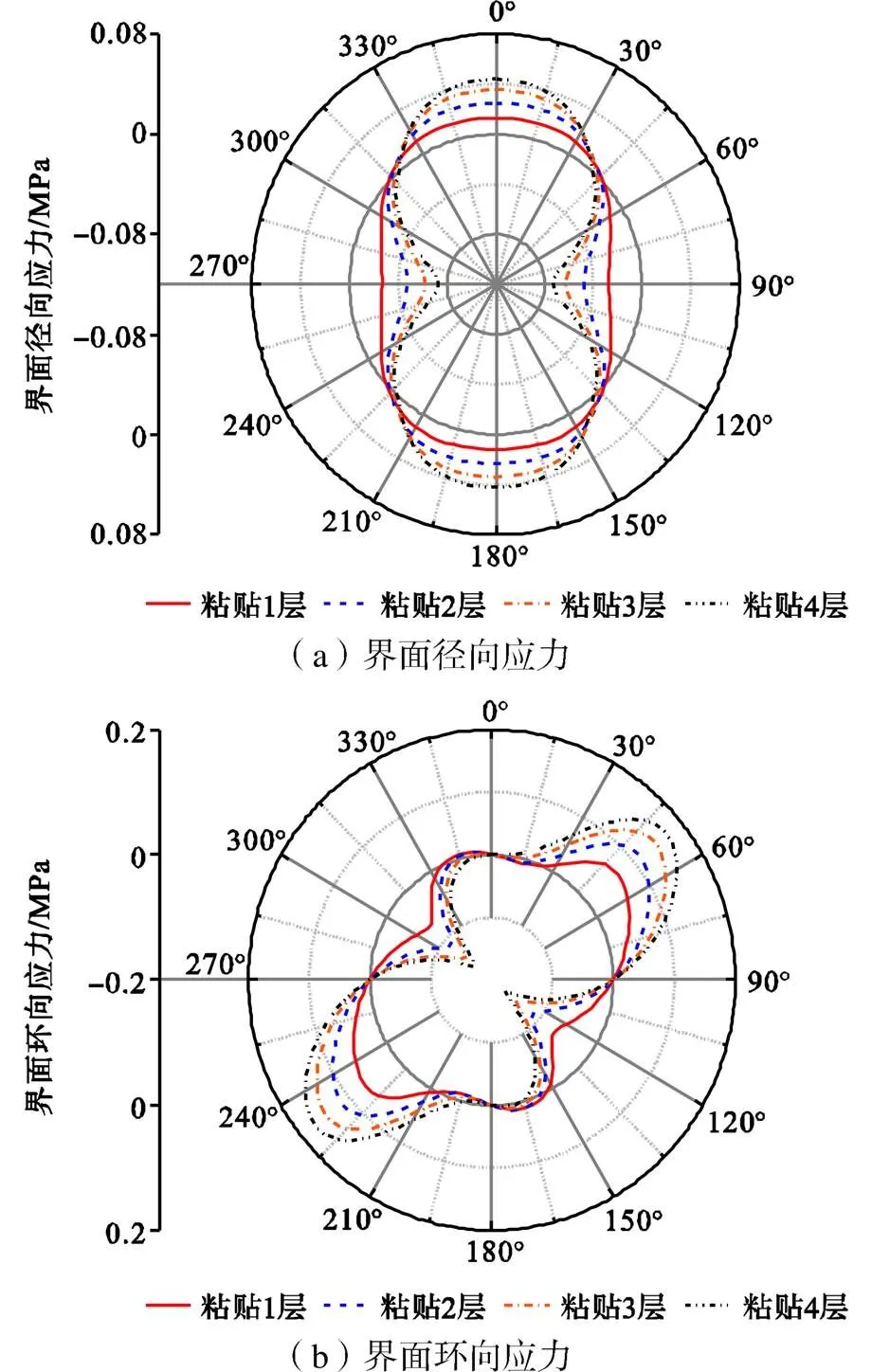
图7 粘贴层数对界面应力的影响

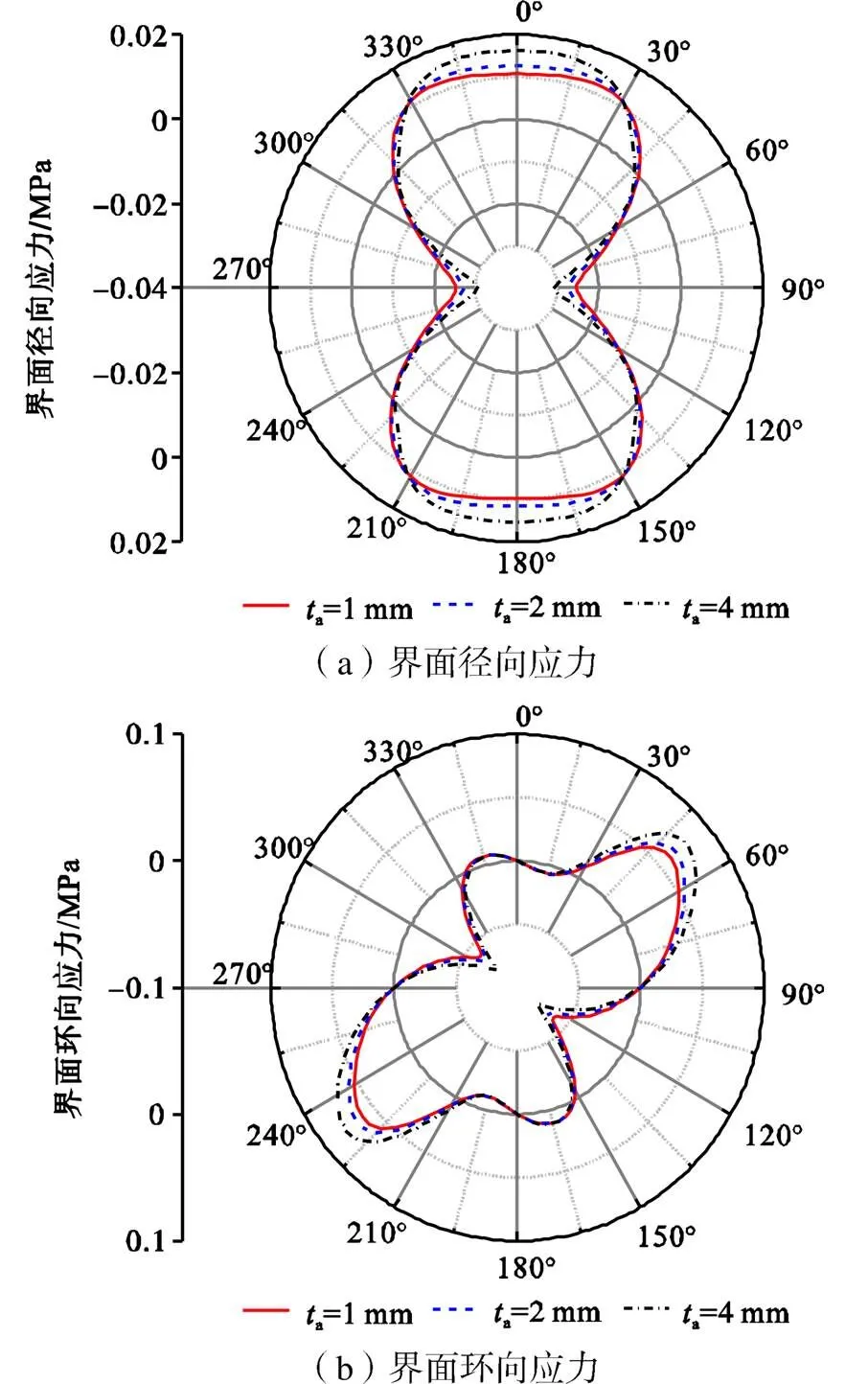
图8 ta对界面应力的影响

2.4.3a对界面应力的影响

从图9可以看出，当a由0.24GPa变化到11.20GPa的过程中，界面最大径向拉应力的增加幅度为81.8%；界面最大环向应力的增加幅度为84.9%.因此，采用内贴CFRP对圆形隧洞进行加固时，宜选择弹性模量较小的胶层．

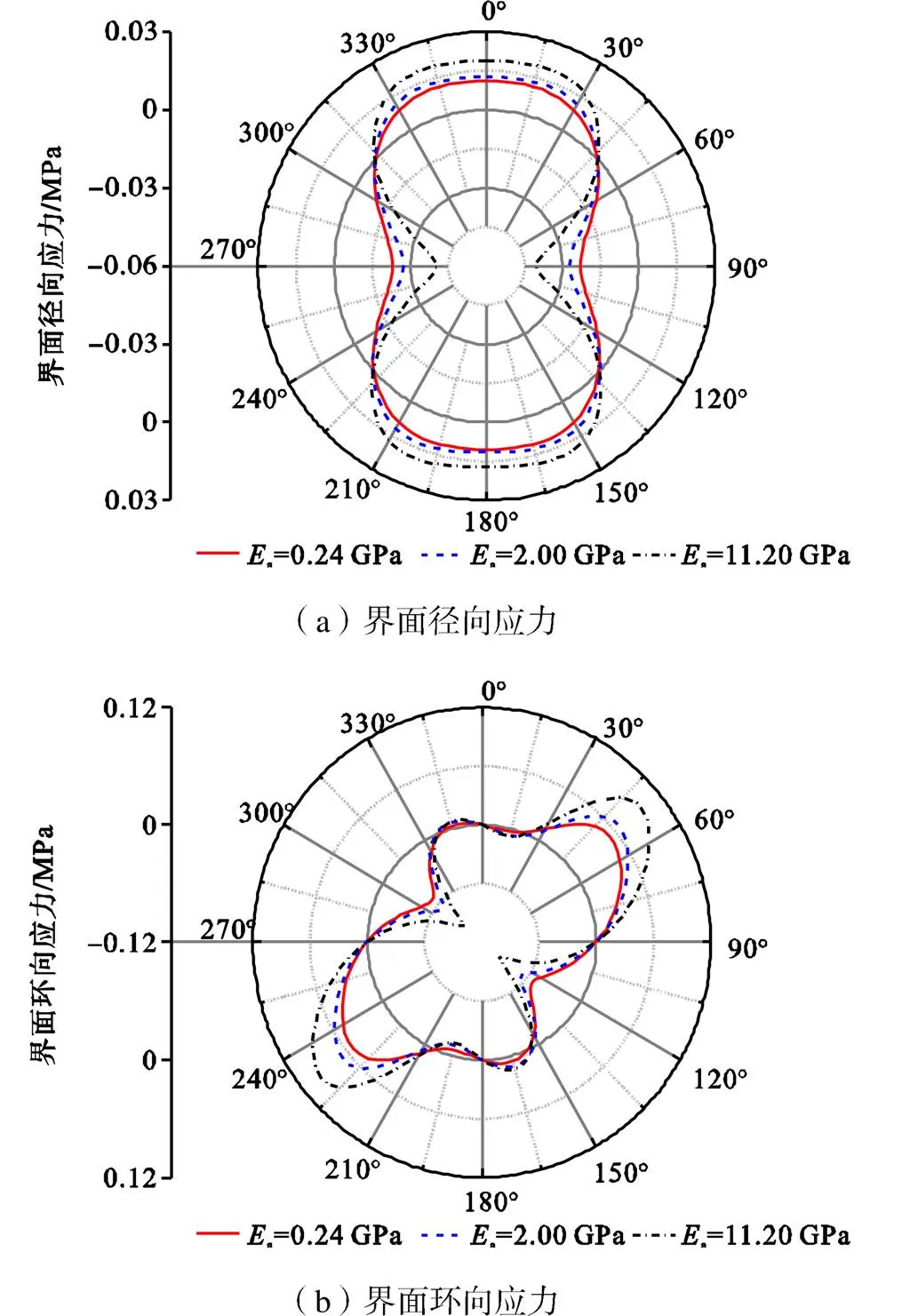
图9 Ea对界面应力的影响

2.4.4c对界面应力的影响

从图10可以看出，当c由100GPa变化到500GPa的过程中，界面最大径向拉应力由0.0072MPa逐渐增加到0.0234MPa，增加幅度为225%；界面最大环向应力由0.0385MPa逐渐增加到0.1112MPa，增加幅度为188.8%，c对界面应力的影响十分明显．CFRP一般分为高强型和高弹模型.对于高强型CFRP，其弹性模量一般在235GPa左右；对于高弹模型CFRP，其弹性模量一般在345～690GPa之间[19]．虽然高弹模型CFRP具有承载性能好、约束裂缝继续扩展的效果明显等优点[20]，但对CFRP与衬砌混凝土的长久共同运行不利．

2.4.5c对界面应力的影响

从图11可以看出，c对界面应力的影响也十分明显，当c由0.10mm逐渐增加到0.20mm的过程中，界面最大径向拉应力和最大环向应力的增加幅度均达到了约50%．在满足加固受力要求的前提条件下，减小c也能明显地改善弧形加固界面的应力状态．类比CFRP层数从1层增加到2层时，界面最大径向拉应力和最大环向应力的增加幅度分别达到约为89%和69%．由此可见，在满足加固强度、同等CFRP用料的条件下，应优先选择增加CFRP的厚度、尽量减少CFRP的加固层数，以此减小界面应力的增加幅度．

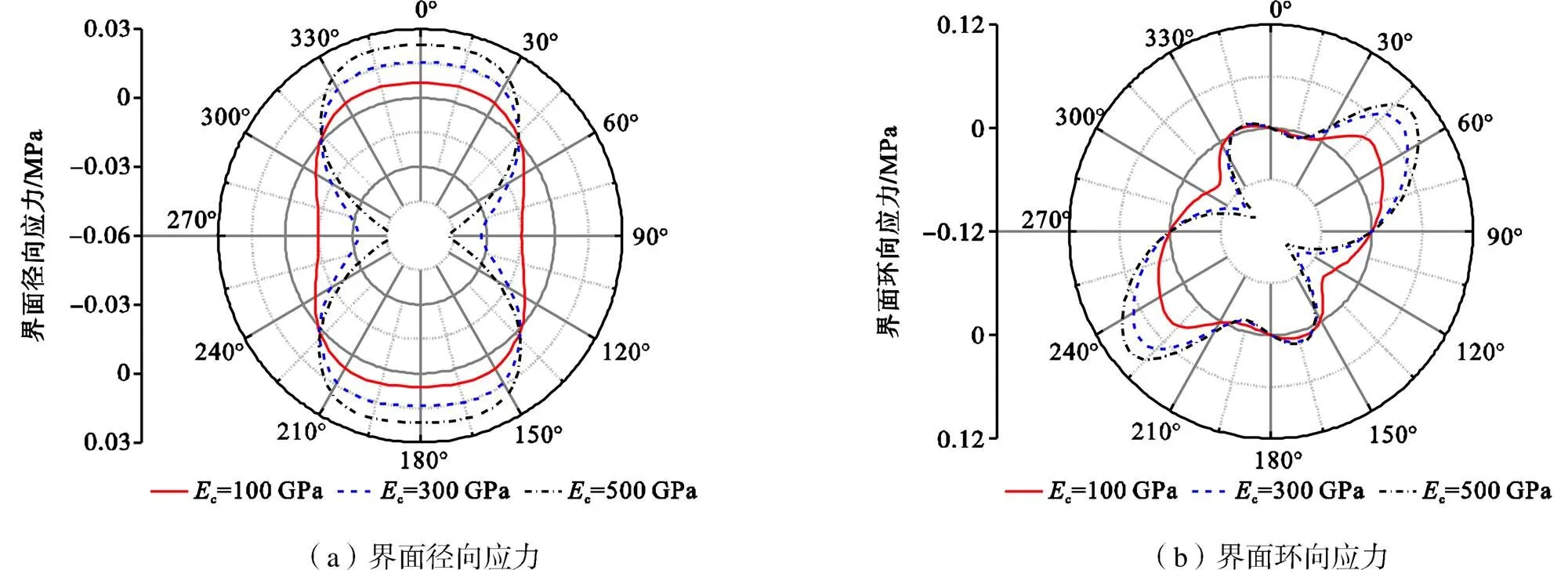
图10 Ec对界面应力的影响

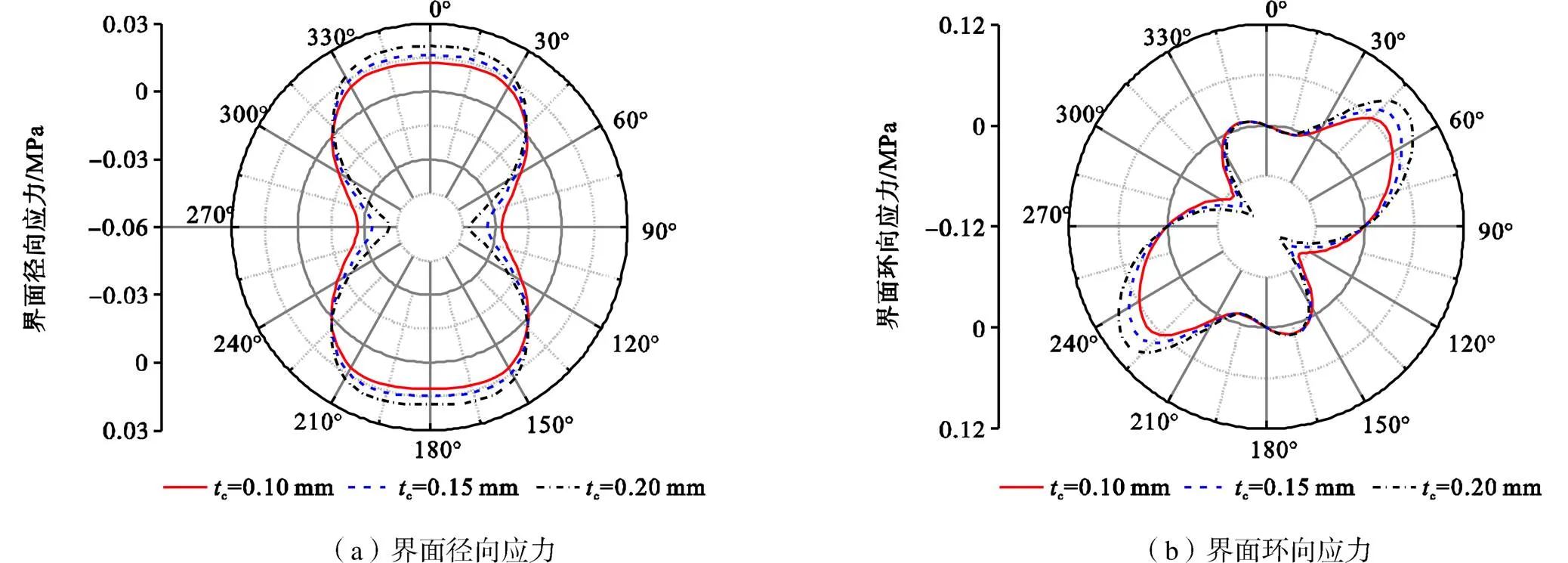
图11 tc对界面应力的影响

3 工程案例

某隧洞采用环锚预应力衬砌，衬砌内径为7m、厚度为0.45m，采用C40混凝土浇筑．每束预应力锚索由12根高强低松弛钢绞线组成，每根钢绞线包含7根钢丝，设计张拉控制应力为1395MPa，沿纵向按照锚索间距0.45m成错位布置．然而，实际建设过程中由于施工缺陷出现了拱顶欠厚情况(部分区段实厚0.28m)．为了防止衬砌在运行工况下导致衬砌混凝土进一步开裂，提出了对欠厚部位灌C25混凝土回填并在内表面上方100°范围粘贴一层CFRP的加固方案，加固参数如表4中的方案1．现对衬砌建立三维有限元模型，有限元模型如图12所示，详细的建模及计算过程见文献[21]．

表4 加固方案

采用William-Warnke五参数破坏准则模拟混凝土开裂情况对加固方案1进行复核，计算结果如图13所示．根据结果可以看出，由于回填混凝土没有预应力效果，在运行工况下基本全部开裂，且方案1的CFRP加固效果不明显，最后导致拱顶沿衬砌厚度方向出现裂缝贯穿的情况．为了提高CFRP加固效果，提出了增加CFRP弹模和厚度，即表4中的方案2．根据计算结果(图13(c))，此时拱顶混凝土开裂情况得到显著改善，未出现裂缝贯穿的情况．然而，结合前文的加固界面应力分析结果，c和c的增加会带来界面应力的增加，使界面容易产生剥离破坏，从而导致加固界面出现新的裂缝(如图13(c)拱肩内表面)．根据前文的分析结果，胶层厚度和弹模的减小有助于减小界面应力，以此对方案2进行优化，通过减小a和a提出表4中的方案3．根据计算结果(图13(d))，方案3中拱顶混凝土裂缝未贯穿，且拱肩内表面未出现新增裂缝．

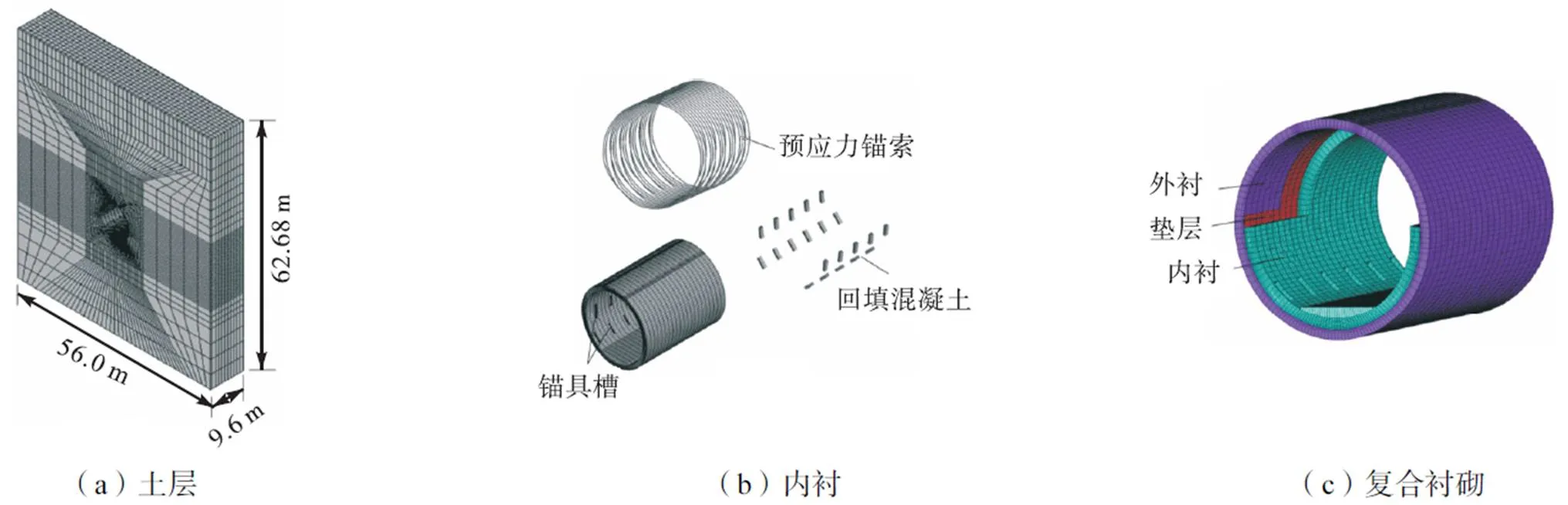
图12 有限元模型

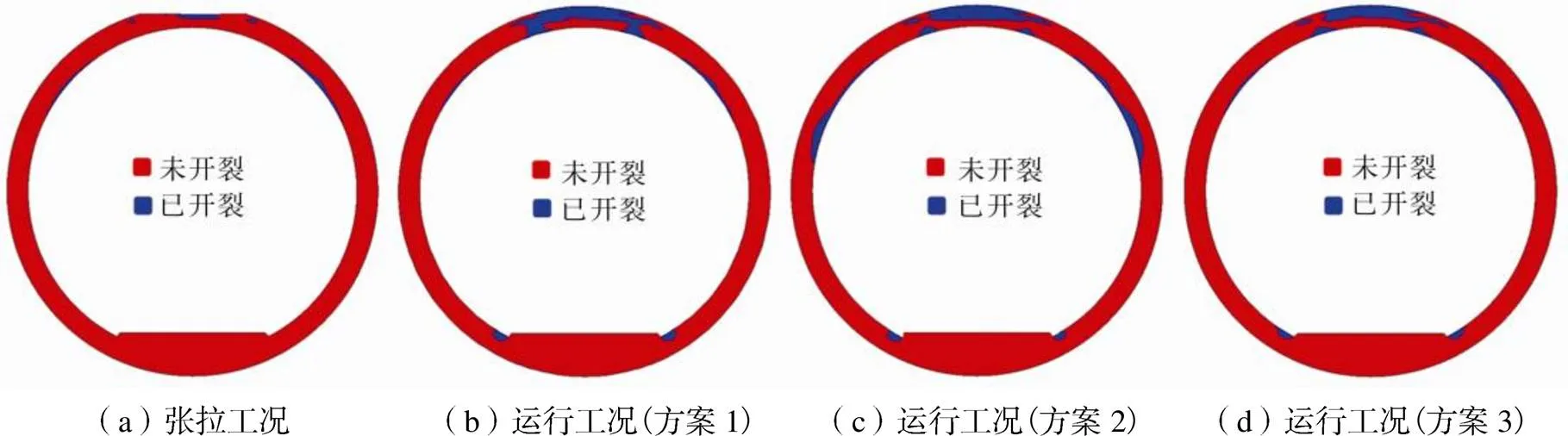
图13 混凝土开裂情况

4 结 论

(1) 理论研究结果表明，界面曲率的变化对界面环向应力无明显影响，但对界面径向应力影响显著．随着界面曲率半径的逐渐降低，界面径向应力会显著提高．

(2) 弧形加固界面复杂的应力状态导致衬砌保护层混凝土处于两种状态：①保护层混凝土径向受压，环向受剪切，径向压应力的存在对防止结构出现剥离破坏有利；②保护层混凝土径向受拉，环向受剪切，径向拉应力的存在会进一步地提高加固界面的应力水平，从而可能导致结构更早地出现剥离破坏．

(3) 数值分析结果表明，胶层的弹性模量和厚度对界面应力有明显影响．在工程实践中，采用CFRP对圆形隧洞进行加固时，选择弹性模量较小的胶层种类同时减小胶层的涂刷厚度可以减小界面的径向应力和环向应力，从而降低结构发生剥离破坏的风险．

(4) CFRP的厚度和弹性模量对界面应力有明显影响，在满足结构受力要求的情况下，建议选择厚度较薄、弹性模量较小的碳纤维材料对隧洞结构进行加固．

(5) 粘贴层数过多，会显著提高加固界面的应力水平，从而可能导致结构过早地出现剥离破坏．在满足加固强度、同等CFRP用料的条件下，应优先选择增加CFRP的厚度、尽量减少CFRP的加固层数，以此减小界面应力的增加幅度．

［1］ 陈锐林，李 康，董 琪，等. CFRP加固钢筋混凝土板爆炸冲击作用下动力响应分析的数值模拟[J]. 铁道科学与工程学报，2020，17(6)：1517-1527.

Chen Ruilin，Li Kang，Dong Qi，et al. Numerical simulation of dynamic response analysis of reinforced concrete slabs strengthened with CFRP under blast load[J]. Journal of Railway Science and Engineering，2020，17(6)：1517-1527(Chinese).

［2］ 王利阳. 纤维材料加固钢筋混凝土压力管道的试验研究[D]. 武汉：武汉大学，2004.

Wang Liyang. The Experimental Study on Pressure Conduit of Ferroconcrete Reinforced by Fabric Reinforced Plastic[D]. Wuhan：Wuhan University，2004(in Chinese).

［3］ Monti M，Renzelli M，Luciani P. FRP adhesion in uncracked and cracked concrete zones[C]// Proc 6th International Symposium on FRP Reinforcement for Concrete Structures. Singapore，2003：183-192.

［4］ Nakaba K，Toshiyuki K，Tomoki F，et al. Bond behavior between fiber-reinforced polymer laminates and concrete[J]. ACI Structural Journal，2001，98(3)：359-367.

［5］ Savioa M，Farracuti B，Mazzotti C. Non-linear bond-slip law for FRP-concrete interface[C]// Proc 6th International Symposium on FRP Reinforcement for Concrete Structures. Singapore，2003：163-172.

［6］ Narayanamurthy V，Chen J F，Cairns J，et al. Effect of shear deformation on interfacial stresses in plated beams subjected to arbitrary loading[J]. International Journal of Adhesion and Adhesives，2011，31(8)：862-874.

［7］ Guenaneche B，Tounsi A，Bedia El A A. Effect of shear deformation on interfacial stress analysis in plated beams under arbitrary loading[J]. International Journal of Adhesion and Adhesives，2014，48：1-13.

［8］ Zhang L，Teng J G. Simple general solution for interfacial stresses in plated beams[J]. Journal of Composites for Construction，2010，14(4)：434-442.

［9］ Oliveira D V，Basilio I，Lourenço P B. Experimental bond behavior of FRP sheets glued on brick masonry[J]. Journal of Composites for Construction，2011，15(1)：32-41.

［10］ Basilio I，Fedele R，Lourenço P B，et al. Assessment of curved FRP-reinforced masonry prisms：Experiments and modeling[J]. Construction and Building Materials，2014，51：492-505.

［11］ Wang J，Zhang C. A three-parameter elastic foundation model for interface stresses in curved beams externally strengthened by a thin FRP plate[J]. International Journal of Solids and Structures，2010，47(7/8)：998-1006.

［12］ Elmalich D，Rabinovitch O. Stress analysis of monolithic circular arches strengthened with composite materials[J]. Journal of Composites for Construction，2009，13(5)：431-441.

［13］ De Lorenzis L，Teng J G，Zhang L. Interfacial stresses in curved members bonded with a thin plate[J]. International Journal of Solids and Structures，2006，43(25)：7501-7517.

［14］ De Lorenzis L，Zavarise G. Debonding analysis of thin plates from curved substrates[J]. Engineering Fracture Mechanics，2010，77(16)：3310-3328.

［15］ Zhang X，Wang P，Jiang M，et al. CFRP strengthening reinforced concrete arches：Strengthening methods and experimental studies[J]. Composite Structures，2015，131：852-867.

［16］ 陆新征. FRP-混凝土界面行为研究[D]. 北京：清华大学，2004.

Lu Xinzheng. Study on FRP-Concrete Interface[D]. Beijing：Tsinghua University，2004(in Chinese).

［17］ Lorenzis L D，Zavarise G. Interfacial stress analysis and prediction of debonding for a thin plate bonded to a curved substrate[J]. International Journal of Non-Linear Mechanics，2009，44(4)：358-370.

［18］ 秦 敢，曹生荣，杨 帆. 胶层对内贴CFRP 加固圆形隧洞受力特性的影响[J]. 天津大学学报(自然科学与工程技术版)，2019，52(1)：62-70.

Qin Gan，Cao Shengrong，Yang Fan. Effect of adhesive layer on mechanical properties of circular tunnel strengthened with CFRP[J]. Journal of Tianjin University(Science and Technology)，2019，52(1)：62-70(in Chinese).

［19］ 秦 鹏. CFRP约束钢管混凝土柱的抗震性能研究[D]. 长沙：湖南大学，2015.

Qin Peng. Research of Seismic Performance on CFRP Confined Concrete-Filled Steel Tubular Columns[D]. Changsha：Hunan University，2015(in Chinese).

［20］ 吴 刚，刘海洋，吴智深，等. 不同纤维增强复合材料加固钢梁疲劳性能试验研究[J]. 土木工程学报，2012，45(4)：21-28.

Wu Gang，Liu Haiyang，Wu Zhishen，et al. Experimental study of the fatigue performance of steel beams strengthened with different fiber reinforced polymers[J]. China Civil Engineering Journal，2012，45(4)：21-28(in Chinese).

［21］ Qin Gan，Cao Shengrong，Yang Fan. Effect of deficiencies in the tunnel crown thickness on pressure tunnels with post-tensioned concrete linings[J]. Advances in Civil Engineering，2018，2018：1-14.

Research on the Mechanical Performance of the Curved Substrate of a Circular Tunnel Strengthened with CFRP Internal Bonding

Shi Zhongqi1, 2, 3，Qin Gan2, 3，Yang Fan1

(1. School of Civil and Hydraulic Engineering，Hefei University of Technology，Hefei 230009，China；2. Shenzhen Urban Public Safety and Technology Institute Co.，Ltd.，Shenzhen 518038，China；3. Key Laboratory of Urban Safety Risk Monitoring and Early Warning，Ministry of Emergency Management，Shenzhen 518038，China)

Carbon fiber reinforced polymer(CFRP)external bonding has emerged as a popular method for the strengthening of circular tunnels. The mechanical performance of the curved substrate is crucial in the strengthening method to ensure the deformation coordination of CFRP and lining concrete. A theoretical analysis model of the arc-strengthened interface is deduced from the bond-slip of the curved substrate. The effects of curvature change on the stress state of the strengthened curved substrate are investigated using analytical calculation results. Special consideration is given to the changes in the interfacial stress state with gradual changes in the elastic modulus and thickness of the adhesive layer，the elastic modulus and thickness of CFRP，and the layers of the bonded CFRP in the numerical model for a circular tunnel strengthened with CFRP. Finally，in conjunction with a specific engineering case，the optimal selection proposals of the above-mentioned parameters are proposed to reduce the interfacial stress and prevent the structure from debonding failure. Assuming that the lining meets the reinforcement conditions，the calculation and analysis results show that the presence of interface curvature causes the strengthened substrate to have not only circumferential stress but also radial stress. The stress state is more complex than that of a planar strengthened substrate. The change in interface curvature has no discernible effect on the circumferential stress but has a significant effect on the radial stress. The radial stress increases significantly as the radius of the curvature decreases. The elasticity modulus and thickness of the adhesive layer have a clear impact on the interfacial stress of the curved substrate. A soft or thin adhesive layer can reduce the interfacial stress and thus reduce the risk of debonding failure. Decreasing the elasticity modulus and thickness of CFRP and reducing the number of strengthening layers can reduce the interfacial stress，which is useful for CFRP and lining concrete working together for a long time.

tunnel reinforcement；curved substrate；interfacial stress；bond-slip；finite element analysis

10.11784/tdxbz202204032

TV332

A

0493-2137(2023)03-0323-09

2022-04-15；

2022-06-15.

施钟淇（1986—  ），男，博士，高级工程师，shizq@szsti.org.

杨 帆，fyang@hfut.edu.cn.

国家重点研发计划资助项目(2019YFC0810702)；中央高校基本科研业务费专项资金资助项目(JZ2022HGTA0335).

Supported by the National Key Research and Development Program of China(No. 2019YFC0810702)，the Fundamental Research Funds for the Central Universities(No. JZ2022HGTA0335).

(责任编辑：金顺爱)