彭阳县参考作物腾发量ET0 预测模型研究

李国强，金建新

（1.甘肃省水利水电工程局有限责任公司，甘肃 兰州 730000；2.宁夏农林科学院农业资源与环境研究所，宁夏 银川 750000）

参考作物腾发量ET0作为确定作物需水量的重要依据，在农业生产中得到了广泛的应用，传统的ET0获取手段为利用Penman-Monteith 公式借助气象参数进行计算，该方法已被广泛验证，是ET0计算的科学可靠的计算方法，但该方法所需要的气象参数较多，需要专业气象站获取[1］。近年来随着机器学习、深度学习等算法的兴起，黑箱模型在预测区域ET0方面已被广泛验证。目前在ET0预测上使用较多的黑箱模型分别为BP 神经网络、遗传算法、小波神经网络、粒子群算法、支持向量机等[2-8］，均取得较好的预测效果，但是不同的算法往往也表现出较大的差异，而且在全年气候变化剧烈、海拔较高等区域，现存的黑箱模型还需要进一步改进[9-10］，而线性方程作为经验性模型，虽然结构简单，但存在较大的区域波动性，需要根据地域气象特征进行参数校核，在使用过程中存在一定的制约[11］。本文通过比较随机森林、BP 神经网络等黑箱方法以及线性方程，筛选出和P-M 法计算结果最为接近的预测模型，建立适合彭阳县ET0的预报模型，为该区域制定适宜的作物灌水方案，实现水资源集约节约使用提供技术支撑。

1 材料与方法

1.1 气象资料来源

气象数据来自宁夏回族自治区气象局与国家气象信息中心，选用彭阳县气象站点2010年～2019 年共10年的气象资料，主要包括地表气象站的逐日平均最高和最低气温、平均风速、平均相对湿度、日照时数等。所有的气象参数都经过了严格的极值和时间一致性检验。

1.2 预测方法

（1）Penman-Monteith 公式法

采用标准彭曼56 法来计算ET0，该方法通过将高度为12 cm，反照率为0.23 以及表面阻力为70 s／m 的草类作为参考作物，该假设准确地模拟了相同生长高度、充足水分和足够营养条件下开阔草地表面的腾发量。其公式为：

式中：ET0是草类的参考腾发量，mm／d；Rn是作物顶层的净辐射量，MJ／（m2・d）；G 是土壤热通量密度，MJ／（m2・d）；T 是2 m 高度处的逐日平均气温，℃；es是饱和水汽压，kPa；ea是实际水汽压，kPa；es-ea代表的是水汽压缺失值，kPa；Δ是水汽压曲线斜率，kPa／℃；γ是湿温计常数，kPa／℃。

（2）随机森林

随机森林（RF）算法是Breiman 提出的基于多棵决策树对样本进行训练，并根据训练得到的模型对待测样本类别进行预测的一种监督学习分类算法。该方法泛化能力强、速度快、稳定性好、精度高等优势。拟合步骤一般分为采用bootstrap 采样、构造决策树、生成随机森林、获取模拟结果等四个步骤，本文中随机森林树的数量选择为300，节点处随机抽取的变量数为3，变量为气象因子，分别为最高温度、最低温度、平均相对湿度、风速、日照时数，在模拟过程中由3 个逐渐增加至5 个分别计算。

（3）BP 神经网络

BP 神经网络 是1986 年由Rumelhart 和McClelland 为首的科学家提出的概念，主要由输入层、隐藏层、输出层以及层级之间连接的网络构成。本文中输入层神经元节点个数分别选择3 个、4 个、5 个，即和引入的气象因子个数一致。输出层神经元个数和目标变量数一致，即始终选择1，隐含层节点个数按照经验选取，这里模拟选择输入层节点数的75%，分别选择2 个、3 个和4 个，即分别构成3-2-1、4-3-1 和5-4-1等3 种神经网络结构，最小训练速率选择0.1，动态参数取0.6，参数Sigmoid 取0.9，允许误差取0.0001，最大迭代次数取1000，对输入节点的数据进行标准化转换。

（4）线性方程

偏最小二乘回归（PLS 回归）是一种统计学方法，是通过投影分别将预测变量和观测变量投影到一个新空间，来寻找一个线性回归模型。因为数据X 和Y 都会投影到新空间，PLS系列的方法都被称为双线性因子模型。集多元线性回归分析、典型相关分析、主因子分析等方法于一体的偏最小二乘回归方法（PLS）更适用于FM 分析，可以避免数据非正态分布、因子结构不确定性和模型不能识别等潜在问题。使用偏最小二乘回归建立最高气温（x1）、最低气温（x2）、平均相对湿度（x3）、平均风速（x4）和日照时数（x5）与ET0（y）的线性关系，不考虑两因素互作和二次项。

2 结果与讨论

2.1 随机森林（RF）

图1 为利用随机森林算法对彭阳县2010 年～2019 年月累计ET0的预测结果。分析可知，在不同气象因子个数条件下，1 月～3 月和9 月～12 月预测值均较Penman-Monteith公式计算结果偏大，在4 月～8 月份则预测值较Penman-Monteith公式计算结果偏小。引入3因子（最高温度、最低温度、平均相对湿度）、4 因子（最高温度、最低温度、平均相对湿度、风速）和5 因子（最高温度、最低温度、平均相对湿度、风速、日照时数）时模拟得到的2010 年～2019 年年平均累计ET0值为1023.6 mm、1030.81 mm 和1001.13 mm，分别较Penman-Monteith 法计算结果小3.2%、2.4%和5.3%。

图1 彭阳县2010 年～2019 年月累计ET0 预测值和实测值

当引入的气象因子逐渐增多时，模拟精度（RMSE）略有改善，但是效果不显著，甚至在增加日照时数因子时模拟精度低于4 因子条件。图2 （a）中当引入最高温度、最低温度、平均相对湿度3 个气象因子时，均方根误差RMSE 为22.85 mm，当引入最高温度、最低温度、平均相对湿度、风速4 个气象因子时，均方根误差RMSE 为22.33 mm（图2 （b）），以及当引入最高温度、最低温度、平均相对湿度、风速、日照时数5 个气象因子时，均方根误差RMSE 为23.15 mm（图2 （c））。可见当气象因子为3 个～5 个时，利用随机森林（RF）对彭阳月累计ET0的预测精度相差不大，整体表现精度较低。

图2 过滤器流量—水头损失关系曲线

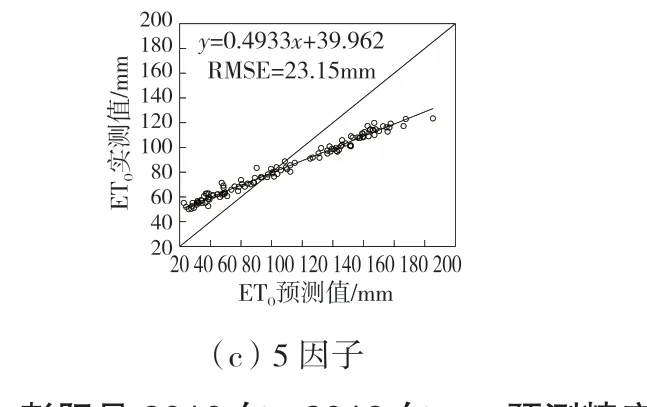
图2 彭阳县2010 年～2019 年ET0 预测精度

2.2 BP 神经网络

图3 为引进3～5 个气象因子利用BP 神经网络对彭阳县2010 年～2019 年月累计ET0预测结果，可以看出基本和Penman-Monteith 法计算结果较为接近，其中3 因子结果较P-M 法均偏小，4 因子模拟结果为1 月、2 月和10 月较P-M法偏小，7 月份较P-M 法偏大，5 因子模拟结果均较P-M 法偏大。引入3 因子、4 因子和5 因子时模拟得到的2010 年～2019 年 年 平 均 累 计ET0值 为995.56 mm、1052.68 mm 和1095.63 mm，前2 个结果分别较Penman-Monteith 法（年均ET0 为1057.44 mm）小5.85%、0.45%，引入5 因子的模拟值较P-M 法大3.6%。

图3 彭阳县2010 年～2019 年月累计ET0 预测值和实测值

图4 为P-M 法和BP 神经网络引入不同气象因子个数条件下模拟得到的月累计ET0，可见当引入3个气象因子时，RMSE为9.80 mm，当引入4 个气象因子时，RMSE 为6.48 mm，当引入5 个气象因子时，均方根误差RMSE 为6.77 mm，可见引入4个以上气象因子时，月累计ET0的模拟效果明显改进。总之当气象因子为3 个～5 个时，利用BP 神经网络对彭阳县月累计ET0的预测精度均较高，特别是引入4 个以上气象因子时，模拟精度进一步提高。

图4 彭阳县2010 年～2019 年ET0 预测比较

2.3 线性方程

彭阳县2010 年～2019 年月累计ET0与不同气象因子的线性回归方程见表1，可以看出气象因子为3～5 个时建立的线性方程其RMSE 介于10.88 mm～19.04 mm 之间，决定系数R2介于0.82～0.94 之间，表现为显著相关。

表1 不同气象因子下ET0 线性回归方程

图5 为分别引入3～5 个气象因子利用线回归方程对彭阳县2010 年～2019 年月累计ET0预测结果，从图上可以看出各因子下1 月份的模拟结果较Penman-Monteith 法计算结果严重偏小，6 月～7 月份模拟结果较P-M 法偏大。引入3 因子、4 因子和5 因子时模拟得到的2010 年～2019 年年平均累计ET0 值为1060.4 mm、1057.4 mm 和1057.5 mm，其中3 因子模拟结果较P-M 法略大（仅大0.28%），而引入4 因子和5 因子的模拟得到的年平均累计ET0和P-M 法基本一致。

图5 彭阳县2010 年～2019 年月累计ET0 预测值和实测值

图6 为引入不同气象因子个数条件下月累计ET0P-M 法和线性回归模拟值， 可见随着引进因子的增加， 模拟精度逐步提高， 特别是引入5 个气象因子时， 模拟精度显著提高。

图6 彭阳县2010 年～2019 年ET0 预测比较

3 结论

（1）利用Penman-Monteith 法计算得到彭阳县2010 年～2019 年年平均参考作物腾发量ET0为1057.44 mm，随机森林（RF）黑箱模型在引入3 个、4 个和5 个气象因子的条件下，模拟得到的平均年ET0分别为1023.6 mm、1030.81 mm和1001.13 mm，分别较Penman-Monteith 法计算结果小3.2%、2.4% 和5.3%， 均 方 根 误 差RMSE 分 别 为22.85、22.33、23.15。

（2）利用BP 神经网络模拟得到彭阳县2010 年～2019 年年平均累计ET0值为995.56 mm、1052.68 mm 和1095.63 mm，分别较Penman-Monteith 法小5.85%、0.45%和大3.6%，RMSE分别为9.80 mm、6.48 mm 和6.77 mm。

（3）利用线性方程模拟得到的彭阳县2010 年～2019 年年平均累计ET0值为1060.4 mm、1057.4 mm 和1057.5 mm，其中3 因子模拟结果较P-M 法大0.28%，而引入4 因子和5因子的模拟得到的年平均累计ET0和P-M 法基本一致。

（4）表明BP 神经网络模型在模拟彭阳县年ET0方面误差最小，精度最高，结果基本和Penman-Monteith 法一致，能较为准确反映ET0的累计值和变化过程。而气象因子从3 个增加到4 个时，预测值显著改善，但当继续增加气象因子时模拟效果提高不显著，甚至会出现降低。