基于人工智能预测岩体条件对TBM 掘进速度的影响研究

袁晓洁，薛新华

（四川大学水利水电学院，四川 成都 610065）

0 引言

在目前很多土木工程大型施工项目中，隧道工程往往是一个重要的行进项目。隧道掘进机（TBM）作为地下隧道工程施工的重要工具，因其具有安全、经济的优势，同时可以避免露天挖掘和爆破所带来的风险而广泛使用[1］。但由于TBM 挖掘工作中对岩体条件极其敏感，往往会导致挖掘工作的效率降低，因此准确地预测TBM 在岩石环境中的掘进性能非常重要，大多数的TBM 性能预测模型都是通过预测ROP 实现。

过去有许多学者基于各种因素与TBM 的ROP 之间的相关性研究，建立了ROP 的预测模型。例如，Gao 等[2］基于长短期记忆（LSTM）神经网络提出的ROP 预测模型；Gong 和Zhao[3］利用非线性回归分析建立起ROP 的统计预测模型。但是一些研究发现这些模型存在无法解决非线性和复杂问题的缺点。

随着计算机科学的发展，基于人工智能对TBM 的性能预测得到广泛应用。Benardos 和 Kaliampakos[4］应用人工神经网络（ANN）建立TBM 推进率的预测模型；Yagiz 和 Karahan[5］将粒子群优化（PSO）用于掘进速度的预测；Grima 等[6］利用自适应神经模糊推理系统（ANFIS）进行TBM 性能的模拟。研究表明利用人工智能算法对TBM 性能进行预测在很多情况下都能提供可靠的结果。

国内外学者通过大量研究发现，ROP 受许多因素影响，因此，很难确定所有的相关参数。实际上，没有必要将所有的变量作为输入参数，因为一些参数之间具有较强的相关性。

本文利用两种人工智能算法，基于三个TBM 隧道项目的185 组数据，选取与TBM 性能有较强的相关性的三个参数（UCS、RQD 和DPW）建立ROP 预测模型。根据四个统计指标对建立的两种模型的精度进行对比分析。

1 人工智能算法

1.1 数据处理组合算法

数据处理组合算法（group method of data handing，GMDH），也称为感应学习算法或自组织算法，是一种模拟大脑进行过程的算法，由Ivakhnenko 于1971 年为预测河流中的鱼群而提出[7］。由于数据处理组合算法具有前馈神经网络的结构，因此人们常将它作为前馈神经网络的一种，称之为多项式网络[8］。图1 所示模型结构是一个典型的4 输入、单输出的GMDH 网络。

图1 GMDH 模型的典型网络结构

GMDH 网络可分为输入层、隐藏层和输出层三部分，首先由输入层（第0 层）各神经元两两交叉组合产生第一层神经元。假设GMDH 网络的第k 层有e 个神经元，那么网络的下一层（第k+1 层）便会产生Ce2=0.5e2-0.5e 个神经元（见图2）。由于GMDH 网络中除输入层神经元外，输出层及各隐藏层神经元之间的关系满足式（1）所示的Ivakhnenko 多项式关系（以图2 中Pk,m神经元为例）：

图2 神经元的产生

式中：Pk,m、Pk-1，i和Pk-1，j分别表示网络中第层中第m、i 和j个神经元的输出值，且P0，i表示网络第0 层（输入层）中第i个神经元Xi；C1～C6均为多项式系数。

GMDH 网络中根据各神经元所对应的输出误差均方差来进行神经元的筛选。图3 是被选中的神经元两两交叉组合产生下一层神经元的示意图。

图3 层内神经元的选择

重复神经元选择的步骤，直至下一层神经元的误差均比上一层的大，则将输出误差均方差最小的神经元作为系统的最终输出。至此，所构造的网络模型即为最优模型。输入和输出参数之间的一般联系可以用 Kolmogorov-Gabor 多项式来表示，如下式所示[9］：

1.2 多表达式编程

多表达式编程（multi expression programming，MEP）是遗传编程（GP）的一种变体，以其多表达能力而突出，可以采用线性染色体编码多个解决方案 。

以 函 数 集F ={*，+，-， ／}和 终 端 集T ={x0， x1， x2}为 例，对MEP 的编码方式进行阐述。图4（a）左边的数字表示基因指数，右边（b）是MEP 染色体通过从上到下的顺序翻译的表达式，它们对应的基因树状图见图5。

图4 桩长30m 时水平承载力与桩径变化的曲线

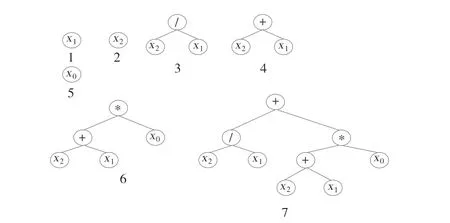
图5 MEP 染色体编码的表达式

由于MEP 染色体可以编码多个解决方案，因此通常通过控制MEP 染色体中所有表达的适应度后，选择出最佳的表达式。一个染色体的适应值通过下列两个公式求出[10-11］：

其中：式（3）为基因的误差计算，i 为基因序号，k 为样本的序号，n 为样本数量，Mk,j为基因的运算结果，Ak为样本对应的实际结果，式（4）为染色体的最终适应值求解公式。

2 数据分析

本文选取来自美国皇后区水隧道项目、伊朗卡拉吉—德黑兰隧道项目和埃塞俄比亚GilgelGibell 水电项目[12，13］的185组数据用于建立预测TBM 掘进速度的模型。鉴于影响ROP的因素较多，本文参考Javad 和 Narges 等[14］的研究，选取与掘进速度有较强相关性的三个参数，即UCS、RQD 和DPW。表1 和表2 分别为数据集的皮尔逊相关性分析结果和统计分析指标。从表中可以得出，选取的三个参数与ROP 的相关性显著，且具有一个较为广泛的分布范围。

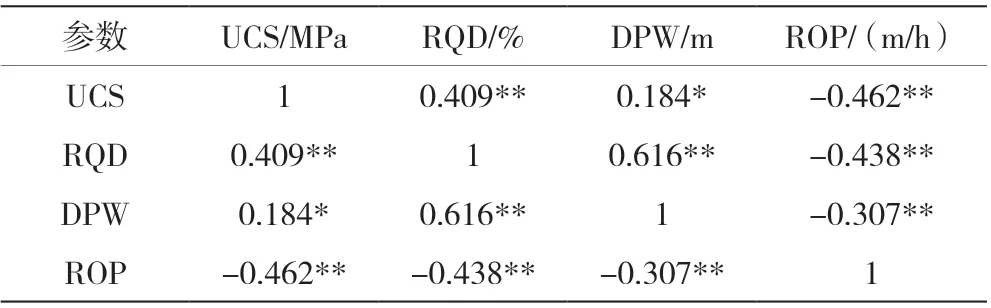
表1 参数的皮尔森相关性分析

表2 实验数据的统计参数

3 模型建立与评价

为了方便对比分析，将收集的185 组数据按照3∶1 的比例划分为训练集（139 组）和测试集（46 组）两部分，用于ROP 预测模型的建立和测试。

3.1 统计指标

首先，为评价三个模型的预测精度，本文选择决定系数（R2）、平均绝对误差（MAE）、均方根误差（RMSE）和相对平方根误差（RRSE）等统计指标。其计算方程式如下：

式中：n 为数据总数；Xm、Xp分别为测量值和预测值；X 为测量值的平均值。

3.2 GMDH 模型

3.2.1 参数设置

为得到最优模型，根据试错策略，本文将隐藏层层数设置为1 层，单层神经元总数限制在3 个以内。输入参数为UCS、RQD 和DPW，输出参数为TBM 的掘进速度ROP，见图6。

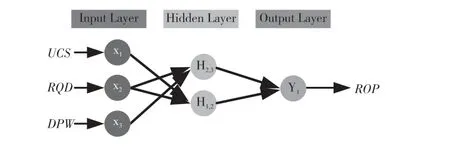
图6 GMDH 预测模型网络结构

3.2.2 GMDH 结果分析

根据上述GMDH 网络结构的参数设置，建立 ROP 预测模型，最优模型的具体结果见表3 和图7。

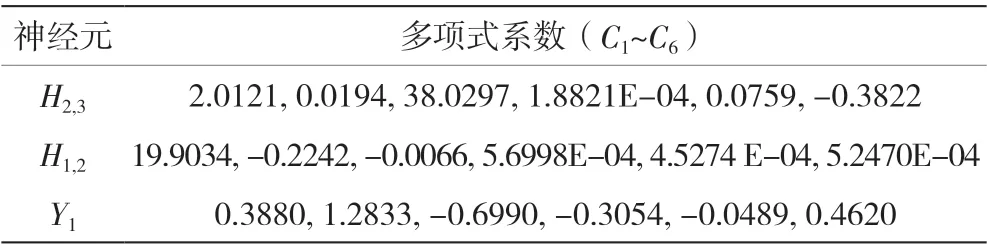
表3 GMDH 模型中的多项式系数总结

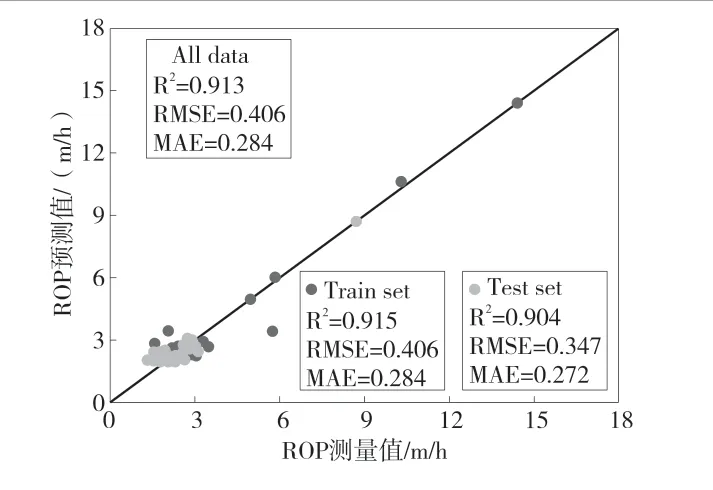
图7 GMDH 模型预测结果和测量结果对比

从图7 中可以得知，训练集的决定系数为0.915，测试集为0.904，总的决定系数为0.913，展现了GMDH 模型预测的可靠性，说明GMDH 模型可以为TBM 的掘进速度提供一个良好的预测精度。

3.3 MEP 模型建立

3.3.1 参数设置

建立MEP 模型首先需要对初始参数进行选择，因此参考Wang 和 Yin[14］研究中的最优参数设置，并与试错法结合，得到表4 中本文的MEP 最优参数设置。

表4 MEP 参数的最优组合设置

3.3.2预测结果分析

结果见图8。由图8 的可得，MEP 模型的训练集和测试集决定系数分别为0.884 和0.919，总的决定系数为0.885，说明基于MEP 提出的预测模型不仅精度良好，且适用于其他隧道项目ROP 的预测，可以为实际应用提供参考。

图8 MEP 模型预测结果和测量结果对比

3.4 模型对比分析

将基于两种人工智能算法提出的ROP 预测模型进行对比，统计指标结果见图9。两个预测模型的结果表明，GMDH模型的决定系数（0.913）高于MEP 模型（0.885）。决定系数作为模型性能的重要决定指标，数值越接近1，则表明这个模型的相关性能越好。对于MAE、RMSE 和RRSE 等三个指标，值越小则模型的预测性能越优。

从图9 的结果中可以得出，两种模型的决定系数都在0.90左右，而另外三个误差评价指标也都低于0.5，表明两种方法都可以在预测ROP 方面提供一个较好的精度。这两种人工智能算法都可以为实际工程的应用提供参考。

图9 三种ROP 预测模型的统计指标

4 结论

1）基于GMDH 和MEP 提出的两个ROP 预测模型都能提供一个较高的预测精度，预测结果与实际测量结果误差较小，它们的决定系数分别为0.913 和0.885，且三个误差评价指标都低于0.5。

2）将GMDH 和MEP 模型进行对比分析，发现两种算法都能提供一个计算公式，但GMDH 的预测精度高于MEP，且GMDH 的计算效率更高，因此，在预测TBM 的性能方面GMDH 可能更适用。

3）本文用于建立模型的数据集来自三个隧道项目，获得的误差较低，如果全部来自同一个项目或局部区域，可能获得一个更低的误差。