不同高径比下浮区晶体生长熔体内对流不稳定性分析

王苗苗，张传成，任 浩，唐绪兵，丁守军，邹 勇，黄护林

(1.安徽工业大学微电子与数据科学学院，马鞍山 243032；2.南京航空航天大学航天学院，南京 210016)

0 引 言

流体在表面张力梯度的驱动下会发生流动，这就是热毛细对流。在浮区法生长晶体过程中，微重力环境下热毛细对流是主要的对流方式。振荡热毛细对流是影响晶体生长质量的主要原因之一[1]。在过去的十几年中，研究人员在空间站和航天飞机内进行了大量的微重力条件下液桥中热毛细对流的研究。研究发现液桥中热毛细对流结构随着Marangoni(Ma)数的变化而不断演化[2-4]。Jin等[5]研究发现流速场沿自由面呈现两个或四个主涡，这些对流涡在较高的Ma数下变得更强。当流体的Prandtl(Pr)数较高时，由表面张力梯度引起的热毛细对流将从二维定常轴对称对流过渡到振荡对流，且振荡对流可通过周向的三维波运动进行描述。Jayakrishnan等[6]对微重力条件下的高普朗特数5 cSt硅油(Pr=67)液桥中热毛细对流的振荡模态进行分解，分析结果表明，液桥自由表面的三维温差所引起的扰动可以分解成各种动态模式，有助于揭示振荡热毛细流动背后的物理机制。Varas等[7]研究了相变材料在微重力下熔化过程中液桥的热毛细效应，结果表明随着Ma数的增大，热毛细对流从稳定对流过渡到振荡对流，并且在振荡对流区，随着Ma数增大先观察到的是热液行波(HTW)模式，然后观察到振荡驻波(OSW)模式。而当流体的Pr数较低时，其表面张力流随着Ma数的增大将会先后出现两次失稳：第一次对流失稳是二维定常轴对称对流过渡到三维定常非轴对称对流；另一次是向三维振荡对流转变。在天宫二号空间站，我国研究人员完成了液桥热毛细对流不稳定波模的空间实验，研究了高径比(Ar)和体积比(Vr)对大Pr数液桥的影响[8]。

对于固定几何比率的圆柱形液桥，三维定常对流的临界Reynolds(Re)数会随着Pr数增大而增大。液桥表面张力流失稳的临界Re数受液桥几何比率、液桥体积、流体物理性质等多种因素的影响。Le等[9]通过采用三维瞬态数值模拟方法，研究了微重力下具有非等圆盘的低Pr数流体(Pr=0.01)半浮区液桥热毛细对流不稳定性的发生和一般特征，介绍了三维稳态热毛细对流和三维振荡热毛细对流的特点。结果表明,在不同圆盘半径比的液桥中，方位流振幅之间的偏差很小，且振动频率随圆盘半径比的增大而减小。

由于不同圆柱体液桥的高径比存在差异，其内部的热毛细对流结构也受到很大影响，同时，在晶体生长过程中高径比明显会限制晶体生长尺寸。Rybicki和Floryan[10]对液桥热毛细对流进行了数值模拟，发现高径比对液桥热毛细流动有重要影响。Velten等[11]通过地面实验研究了高径比对液桥热毛细对流的影响，结果表明当高径比增加时，临界Ma数逐渐减小。Chen和Hu[12]利用线性不稳定性分析方法，研究了微重力环境下半浮区对流的毛细不稳定性，分析了液桥体积和高径比对临界Ma数的影响。研究发现，在大Pr数和小高径比的情况下，临界Ma数与液桥体积的关系曲线中存在一个间隙区域，在该区域内不会观察到振荡对流。Fan等[13]数值模拟了不同高径比对热毛细对流形成过程中的流动结构影响，其中定义了强对流区(靠近界面)与弱对流区(位于液桥中心)的概念，得出强对流区的范围在高径比增大到1以后趋于稳定。Kuhlmann和Nienhüser[14-15]报道了液桥自由界面的动态变形是由流体动压、黏性应力、液桥体积、表面张力和流体静压等因素共同决定的，而热毛细对流的不稳定性则取决于液桥的高径比和自由表面的形状。

熔体中产生的振荡热毛细对流对生长晶体的质量有极大负面影响。对于具有高导电性的硅、锗熔体，这类晶体在生长过程中大多选择施加磁场来抑制有害流动。Dold等[16]实验研究了旋转磁场强度对掺杂硅浮区生长的影响，同时对流体流动进行了数值模拟。研究结果表明：在旋转磁场作用下，时变三维流动转变为准轴对称运动。Walker等[17]研究分析了旋转磁场下浮动区熔体流动的线性稳定性。结果表明，在没有旋转磁场的情况下，熔体流动会存在一系列不稳定性，使晶体中出现生长条纹。由旋转磁场的洛伦兹力引起的方位角速度可以降低这些不稳定性，他们的结论与Dold等[16]的实验结果一致。

综上所述，影响液桥热毛细对流不稳定性的因素有很多，如高径比、温差、磁场构形等。目前大多数文献报道都是采用半浮区液桥模型进行的研究。半浮区液桥模型结构简单、边界条件容易确定。研究者们通过固定半浮区液桥半径，改变圆柱形液桥高度的方法对不同高径比下热毛细对流的稳定性作了较为细致的描述，但关于振荡热毛细对流的产生及演化规律仍需进一步研究。本文通过固定半浮区液桥的高度，改变圆柱形液桥的半径，探索热毛细对流的稳定性与高径比之间的关系。

1 物理数学模型

计算所使用的物理模型为柱坐标系(r,θ,z)下的半浮区液桥模型，如图1所示。不考虑零重力条件下自由面的形变，液桥自由面可近似为圆柱面。液桥悬浮在两个半径均为R的同轴圆盘之间，其高度为L。在位于z=-L/2和z=L/2处，视固液界面处液体速度为零，并使温差ΔT(ΔT=Th-Tc)保持不变。

图1 物理模型

σ=σ0+γTT

假设熔体是一种不可压缩性的牛顿型黏性流体，作用于自由表面上的表面张力的大小可表示为以σ0为初值、以γT为比例系数的线性函数：

(1)

式中：γT=∂σ/∂T，熔体的其他物理特性不变。

在上述假设条件下，熔区内N-S方程组可表示为：

(2)

(3)

(4)

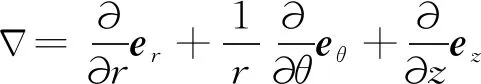
边界条件和初始条件设定如下：

当z=-L/2时，T=Tc

(5)

当z=L/2时，T=Th

(6)

(7)

(8)

式中：n是熔体表面的法向单位矢量，方向指向面外。硅熔体物性参数[18-19]及计算需要的其他参数如表1所示。

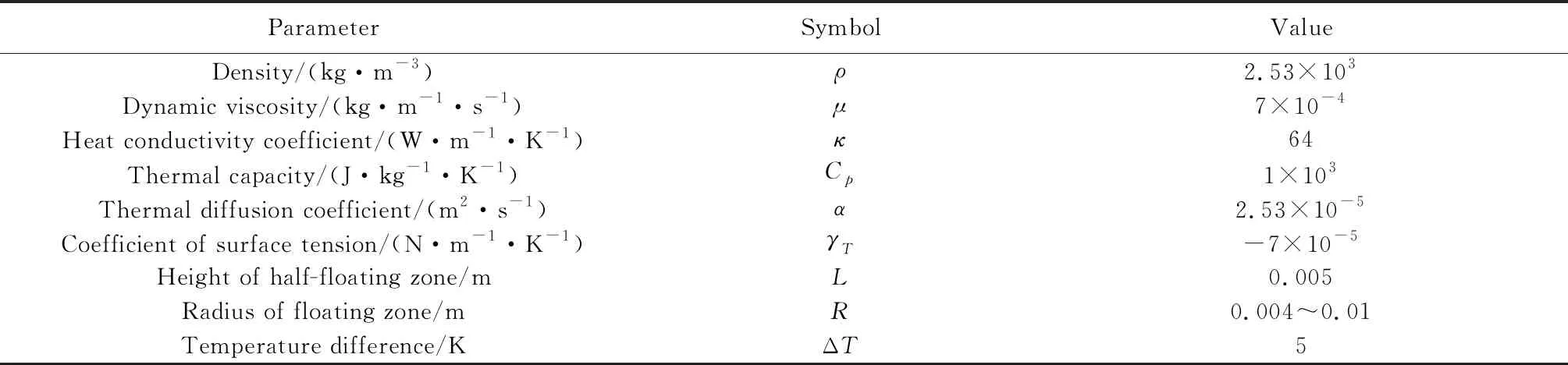
表1 硅熔体物性参数[18-19]和其他计算所需参数

2 计算方法

采用结构化网格将计算区域进行划分，为提高计算精度，在上下底面及熔体表面处进行局部加密，如图2所示。当R=10 mm时，验证网格独立性，其独立性验证曲线如图3所示，综合考虑计算精度和计算时间，挑选40r×80θ×80z(对半径R=5 mm和R=4 mm的液桥选取30r×80θ×80z)的网格开展数值计算。在计算中，设置时间步长为10-3s。采用有限体积方法对控制方程进行离散，非稳态项采取二阶隐式推进法。采用PISO算法的压力速度耦合，对流项采用QUICK格式，扩散项采用二阶中心差分格式。将该算法的结果同Levenstam等[20]的结果进行了比较，表2为在Pr=0.01，Re=3 500时，两者的对比结果。从中可以看出吻合度很高。

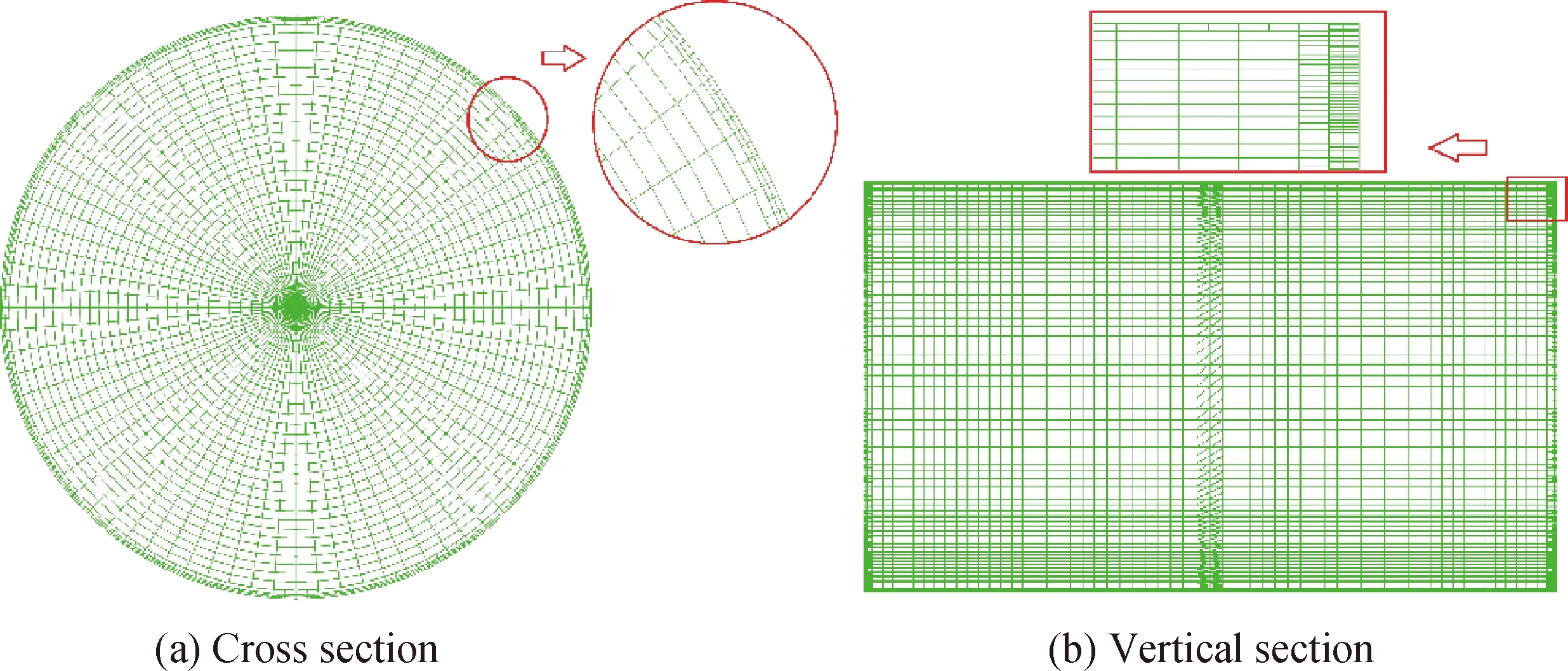
图2 网格划分

图3 网格独立性验证曲线

表2 本文和 Levenstam[20]的计算结果对比

3 结果与讨论

在零重力环境下，由重力引起的自然对流消失，此时，由表面张力梯度引起的表面张力流起主导作用。熔体的表面张力与温差密切相关。当熔体的上壁面和下壁面之间存在温差时，在流体的自由表面上将会产生表面张力梯度，因此，驱动着自由表面附近的流体从热端流向冷端，根据质量守恒原理，从冷端流向热端的回流在熔体内部产生，从而形成一个对流循环。当高径比Ar=0.5时，熔体对流表现出明显的三维对流特征，此时z=0切面上的速度分布如图4(a)～(c)所示。因为表面张力驱动的轴向速度并不相等，导致熔体回流速度在自由表面附近也具有方向角性，在熔体中心轴周围，轴向速度又一次变为负值。径向速度在切面上形成两对中心对称分布的径向波，切面上的周向速度形成的涡胞也成对出现，在熔体中心轴附近形成两对中心对称分布的涡胞，在外围区域则形成与之对应的两对中心对称分布的涡胞，形成完整的对流胞单元。数值结果表明，在切面中心区域，熔体沿周向从高温区流向低温区，从而形成了逆时针和顺时针交替进行的四个对流涡胞单元；而在熔体表面附近区域，对流则从低温区流向高温区，这同表面张力流方向恰好相反，说明周向涡胞的形成与周向上的温度差无关。

由于对流的影响，如图4(d)所示，熔体z=0切面上的温度分布表现为明显的非轴对称性：在切面外围边沿区域形成了一对低温区和一对高温区，由于高温区附近的径向温度梯度远大于低温区域的径向温度梯度，这样在熔体内部也形成了一对与表面处的高温区相对应的低温区。对比图4(a)和图4(d)不难发现，温度等值线结构和轴向速度等值线结构具有很高的相似性，说明切面上温度分布受轴向速度影响很大，在轴向速度出现极值的位置，温度也相应地出现极值。

在熔体表面附近和内部区域各选取一个监测点，监测点的温度和轴向速度随时间的变化过程如图4(e)、(f)所示。从图4 (e)、(f)可以看出，流动时间t>125 s后，监测点温度和速度都不随时间的变化而发生变化，熔体处于稳态对流模式。

图4 Ar=0.5时z=0切面上的速度、温度分布和监测点温度、轴向速度随时间的变化

当Ar=1时，熔体中的对流模式从三维稳定流动转变为多频振荡流动。首先来分析z=0切面上的速度分布。从图5(a)可以看出，在某时刻，熔体的轴向速度在z=0截面上的分布具有方向性，并且在熔体表面，表面张力流动的速度高于Ar=0.5时的速度；与Ar=0.5时中心区域轴向速度为负值的情况不同，Ar=1时，切面上靠近中心轴的区域完全被回流占据。图5(b)和图5(c)显示了z=0切面上相应的径向和周向速度分布。与Ar=0.5时的径向速度分布相比，Ar=1时的径向波结构也是中心对称分布，但轴向波的方位不同；随着不稳定性的增加，自由界面处的周向波被熔体中心形成的周向波挤压，其占据面积明显小于Ar=0.5时的面积。温度分布如图5(d)所示，熔体表面附近存在一对热区和冷区，这与Ar=0.5时相同。不同之处在于，Ar=1时，因为回流占据了熔体的整个中心区域，所以最低温度点出现在切面中央位置附近。

图5 Ar=1某时刻z=0切面上速度、温度分布和监测点轴向速度、温度随时间变化与频谱图

同样在液桥自由表面附近和内部区域分别选取两个监测点，监测点轴向速度和温度随时间变化情况如图5(e)、(f)所示，其对应的频谱如图5(g)、(h)所示。轴向速度和温度随时间呈周期性变化且振荡频率相同，这个结果表明，温度振荡是由热毛细对流振荡引起的。自由表面附近监测点(4.9 mm,0,0)的振荡主频为f1=0.174 Hz，二次谐波频率为f2=0.347 Hz，熔体内部监测点(2.5 mm,0,0)处振荡主频为f2，二次谐波频率为f1，表明在熔体内部热毛细对流的不稳定性被放大，频率增加了一倍。此外，还发现了多个谐波频率，谐波频率之间均满足倍频关系fn=nf1。

温差ΔT=5 K保持不变，半径继续减小至R=4 mm (Ar=1.25)。图6显示了不同时期监测点轴向速度和温度的变化以及相应的频谱图。从图6(a)可以看出，当流动时间t=25 s时，监测点速度和温度已经呈现周期性振荡，随着时间的增加，速度平均值也在缓慢上升。当t>100 s时，速度和温度的平均值均呈显著上升趋势，监测点轴向速度分别在t=275 s和t=420 s时达到峰值，然后略有下降。当t>500 s时，轴向速度的平均值及振幅均不再随时间变化。如图6(b)显示各监测时段温度振荡的平均值和振幅均在缓慢下降；t>450 s时，温度振荡完全消失。这是因为轴向速度在等幅振荡模式的振幅很小，不足以使温度发生振荡。

图6 Ar=1.25时各个时间段内监测点轴向速度、温度变化情况和频谱图

如上所述，在流动的初始阶段(t<400 s)，轴向速度和温度不仅随时间振荡，而且它们的平均值也发生变化。但根据频谱分析发现，温度和速度的振荡频率是相同的，不同监测点的振荡频率也是相同的，都属于单频振荡模式。图6(c)显示了t=25～100 s不同监测点的频谱图，从图中可以看出，自由表面和熔体内部的温度以及轴向速度的振荡频率f=0.398 Hz。当400 s500 s)的振荡主频率完全相同。

随着Ar的变化，熔体内的对流会呈现出多种形态。图7(a)～(c)为t=500 s时，不同高径比下子午面θ=0上的流线分布和温度等值线。当Ar=0.5时，子午面θ=0上的流线左右对称，两边的涡心在同一高度上。在熔体内部，熔体水平流向中心区域，在中轴线附近交汇后一分为二，大部分熔体流向低温面，在低温面附近形成不完全的回流涡，剩余小部分熔体在交汇后向上底面流去。在对流影响下，温度等值线在熔体中心轴和自由表面附近向下弯曲，而在熔体向上流动的区域，温度等值线则向上凸出，因此等温线的轮廓呈现字母“M”的形状。当Ar=1时，左右两边对流涡胞的涡中心沿轴向稍微向下移动，涡中心高度相同，仍位于z=0横切面附近。此时中心区域有熔体流过，左右对称的对流结构遭到破坏。在靠近低温面的中心带，有一对对流较弱的回流涡胞发育形成。子午面上的等温线在自由表面附近向下弯曲，在中心附近区域则向上隆起。当Ar=1.25时，对应R

图7 不同高径比下子午面(θ=0、π/2)上流线和温度等值线

因为ΔT=5 K时的流动均表现为三维结构，子午面θ=π/2上的对流模式和温度分布相较于θ=0面上的有所不同，结果如图7(d)～(f)所示。当Ar=0.5时，流线结构围绕中心轴对称分布。位于中轴线上的高温区域的熔体由左右分别流向自由表面，对流涡心在子午面两底角位置。由于对流涡胞的核心区域只占子午面极小部分，所以温度分布主要由热扩散决定，在对流涡胞影响较大的两底角附近，温度等值线向下弯曲，其余部分则保持水平状态。当Ar=1时，流线结构与θ=0面上的流线结构相似，但中心区域的流体的流向同θ=0面上的正好相反。温度分布与θ=0面上的分布大致相同。当Ar=1.25时，整个熔体空间被左右两个热毛细对流涡胞占据，在左半部分表现逆时针流动而在右半部分表现顺时针流动。此时温度等值线在靠近中心轴处向上凸出的程度增加，在靠近自由表面处则向下弯曲程度更高。

4 结 论

对于熔体高度为5 mm的半浮区模型，采用数值模拟的方法，研究了零重力条件下温差为5 K的熔体中热毛细对流的动态特性，分析了高径比变化对热毛细对流的影响。阐明了热毛细流动的转捩过程及振荡模式，加深了对浮区内热毛细流动特性的认识，模拟结果可为晶体生长工艺优化提供指导和借鉴，具有重要科学意义和应用价值。主要结论如下：

(1)当Ar=0.5时，熔体对流表现为三维稳态结构；当Ar=1时，熔体对流由稳态对流变化为多频振荡对流，不同监测点的物理量振荡的主频率各不相同，但同一监测点的速度和温度具有相同的频谱结构，主频和各谐频之间满足倍频关系fn=nf1；当Ar=1.25时，熔体开始时表现为单频振荡模式，其振荡幅度随时间逐渐衰减，经过一段时间，温度振荡消失，最终，监测点轴向速度演化为小幅振荡模式。

(2)熔体内温度分布受对流影响很大，温度等值线随熔体流向发生弯曲。不同高径比下，在接近自由表面的位置均形成两对冷热交替的区域，无论是稳态流动还是振荡对流，冷热区域的方位角位置都几乎不随时间变化而改变。