天梯系统设计及其力学问题研究进展

刘雪峰 崔乃刚 汪小卫 凡友华 罗世昊

(1.中国民航大学航空工程学院, 天津 300300; 2.哈尔滨工业大学航天学院, 哈尔滨 150001;3.中国运载火箭技术研究院研究发展中心, 北京 100076; 4.哈尔滨工业大学(深圳)理学院, 深圳 518055)

1 引言

早在1895 年,航天之父Konstantin Tsiolkovsky 就提出了天梯(Space Elevator, SE)的概念:从赤道建一座高塔,由地面与对地静止轨道(Geostationary Orbit, GEO)的空间站连接,当设计参数合适时,天梯受到的重力与随地球自转的离心力相抵消,天梯受到的合力可以为零。

天梯的优点是能够持续不间断地向空间站运送货物,据估算,每周可以将上百吨的货物运送到空间站[1]。 而目前世界上推力最大的重型猎鹰运载火箭单次到达GEO 的运载能力也不超过26.7 t,而且需要较长的发射准备时间。 除此之外,天梯的运输成本相比于运载火箭也有巨大的优势。 目前估算的天梯运输成本可以低于100 美元/公斤,而运载火箭则高得多,例如重型猎鹰运载火箭运送到GEO 的成本达到了3370 美元/公斤[2],而且未来天梯可能利用太阳能提供能源,因此天梯在经济性和环保性方面都优于传统的运载火箭。

天梯可以用于卫星或飞船的释放,尤其是从天顶锚以高速释放飞船,使地球到火星仅需61天;分步将空间站的部件运送到在建的空间站上,从而组建大型的空间站;将其他星球上开采的矿石运送到地面;用于捕捉太空碎片并集中处理;利用其超强的运载能力开展更广泛的太空科学实验,开发太空旅游项目;除此之外还有更多待开发的应用范围。

尽管天梯有很多优点,但是在1979 年,Pearson 通过估算发现制造天梯的材料所需的强度远高于钢材等常规材料,使得天梯系统的可行性受到影响[3]。 直到1991 年人们发现了碳纳米管材料,使天梯的研究重现曙光。 碳纳米管的抗拉强度可以达到钢材的100 倍以上,能够满足天梯制造所需的强度。 中国的科研团队在2013 年已经可以制造半米长的碳纳米管[4],未来人们将会有能力制作更大尺寸的碳纳米管,从而使天梯的制造成为可能。

在碳纳米管材料发现之后,有关天梯的研究越来越多。 美国国家航空航天局(NASA)在1999年对天梯系统的可行性进行了分析,认为天梯在未来是可以实现的[5]。 在此之后,Edwards 等[6-7]对天梯系统的可行性、设计及主要参数等进行了一系列的研究,为之后的相关研究打下了基础。2015 年,汪小卫等[8]对目前国内外天梯相关的研究进展进行了介绍。

目前对于天梯的研究主要集中在结构设计及力学问题两方面,其中结构设计是力学问题研究的基础,不同结构的天梯对应着不同的力学问题。本文介绍天梯系统的分类,对天梯设计、力学计算和振动控制方面的主要研究进展进行综述。

2 天梯分类

天梯布置不同,其受力特征就不同,根据天梯的位置,天梯系统分为地球天梯、月球天梯和火星天梯等,其中地球天梯还可以细分为布置在赤道上的赤道天梯和布置在非赤道位置的非赤道天梯。 除了完整的天梯以外,还有一种介于完整天梯和绳系卫星系统之间的部分天梯(Partial Space Elevator, PSE),它不像完整天梯这样一直延伸到地面,而是更像超长的绳系卫星,需要将载重通过飞船等运送到近地点,然后再通过PSE 运送到更高的位置。 由于其与完整天梯的受力规律有一定相似之处,在有些方面的研究中与完整天梯类似。

最常见的天梯是地球赤道天梯,即地面锚固段建立在地球的赤道上,其核心结构包括地面锚固端、攀爬器、绳索及天顶锚,结构示意图如图1所示[7]。 对于地球赤道天梯,绳索垂直于地球表面,在不考虑外界扰动时,绳索受到地球引力及随地球自转的离心力作用,地球引力方向与其轴向重合。 通过调整结构参数,可以使地面对天梯的作用力为零,或者等于一个预期的取值。 所有的受力均在绳索的轴向,可以达到受力的平衡。

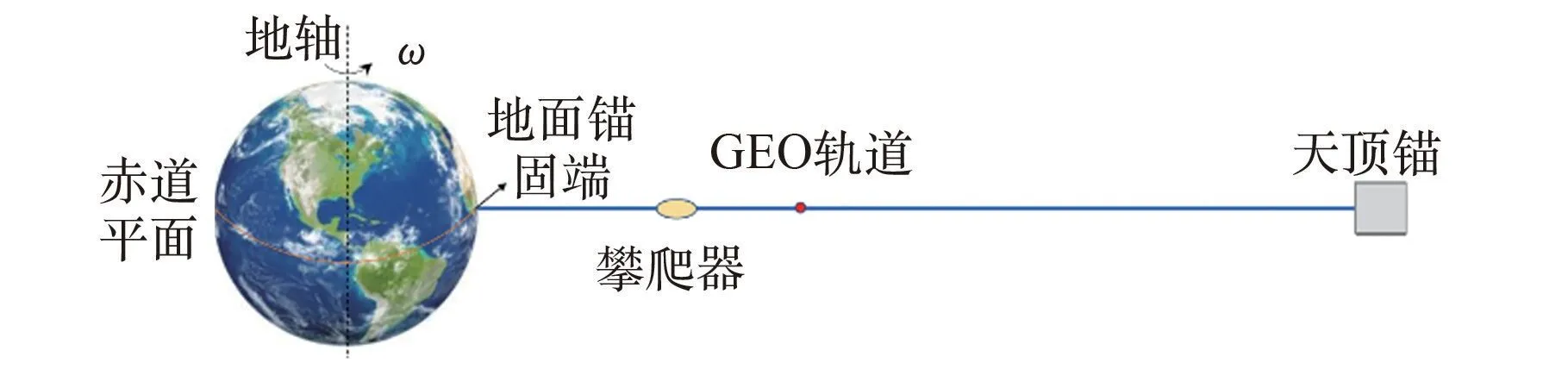
图1 地球赤道天梯结构示意图[7]Fig.1 Schematic diagram of earth equatorial space elevator structure[7]

除了最常见的地球赤道天梯以外,还有建立在地球非赤道表面的天梯,以及建立在月球上的天梯,这里统称为非地球赤道天梯。 非地球赤道天梯的受力与地球赤道天梯有所区别,例如地球非赤道表面天梯的重力不在绳索轴向,而月球天梯需要同时考虑月球和地球引力等。 这造成非地球赤道天梯对应的力学方程与地球赤道天梯有所区别。

由于目前已经有大量的GEO 轨道卫星,地球赤道天梯容易与其发生干扰而影响安全性。 将天梯建造在非赤道的低纬度地区的地球非赤道天梯可以解决这一问题,但是这种情况下绳索的重力不在轴向,增加了其设计难度。 Gassend[9]给出了地球非赤道天梯截面积的近似解;2019 年,Wang等[10-11]建立了地球非赤道天梯的静力学模型,发现提高系绳材料的抗拉强度可以扩大天梯系统的部署范围,并且建立了动力学方程,对其振动模态进行了分析。

在月球天梯方面,宋海蓝等[12]提出了一种月球天梯系统模型的建立方案及太空舱的运行方式,从而初步计算了能耗;Liu 等[13]研究了月球空间系绳系统的非线性动力学及其潜在应用,建立了动力学方程;王晓慧等[14]研究了L1 点月球天梯的振动抑制问题;Shi 等[15]研究了月球PSE 由于攀爬器造成振动的减振问题。

此外,Cowan 等[16]还提出了火星非赤道天梯的概念,并且给出了静力学平衡方程。

目前对于地球赤道天梯的结构设计和相应力学问题的研究已经广泛地开展,并且越来越深入,而布置在其他位置的天梯研究相对较少。 事实上,在其他位置的天梯的主要研究方法和难点与地球赤道天梯接近。

3 天梯设计研究

对于天梯系统的设计来说,最大的难点在于其达到受力平衡时绳索受到的轴向力过大。 Aravind[17]通过估算发现当天梯的截面随高度没有变化,即等截面天梯情况下,绳索的正应力达到了382 GPa,远高于钢等传统材料的抗拉强度。

若使用纳米碳管材料,设置地面锚固端绳索的应力为0 时,推导出天梯系统任意截面处的应力为式(1):

其中,G为万有引力系数,M是地球质量,ρ是天梯绳索的密度,Re是地球半径,Rg是同步轨道半径,L是天顶锚在地心坐标系的坐标。

此时天梯系统最大应力可以减小到60 GPa左右,但是降低天梯系统绳索的工作应力仍然是天梯设计最重要的问题[18]。

将天梯的截面设置成随高度变化,而使得应力随高度不变,即变截面天梯,能够有效地降低绳索的应力,其基本结构如图2 所示。

图2变截面天梯结构示意图Fig.2 Sche matic diagramofvariablesection space elevator

2007 年,Cohen 等[19]发现变截面绳索使天梯的应力显著降低,并给出了等应力状态下变截面天梯截面积的表达式如式(2)、(3)所示。

其中,s为天梯绳索上任意点到地面锚点的距离;Am为渐变截面天梯系统同步地球轨道处的横截面积,也就是天梯绳索最大的横截面积;ε0为天梯绳索的应变,在渐变截面天梯系统中为常数;h-为渐变截面天梯系统的特征高度,如式(4)所示。

其中,σ0是渐变截面天梯系统的设定应力,为恒定常数,ρ为天梯绳索材料的密度,g0为地球半径处的重力加速度。

在这种情况下,使天梯的应力显著降低。 目前多数天梯的研究都是在变截面天梯的基础上进行的。 Dan 等[20]从生物学中获得灵感,提出可以降低天梯结构的安全裕度,即在天梯设计中提高工作应力比,同时令材料可以随时自我修复,通过计算发现在这种情况下,M5 材料制造的天梯即可以满足设计要求。

2021 年,石润[21]提出分段式天梯(图3)的概念,即天梯的截面积分段改变,并对其力学问题进行了初步的研究。 这种分段式天梯比等截面天梯应力更小,比变截面天梯更容易加工制造,而且可以以同步轨道上的空间站为起点同时向上和向下分段建造,跟以往的设计方案相比有很多优点,为未来的天梯设计提供了新的思路。 目前,通过合理的设计,使天梯绳索承受的应力减小到40 GPa左右,如果能进一步减小应力,就可以显著增加天梯绳索的适用材料种类,从而突破材料限制,有助于天梯早日应用。

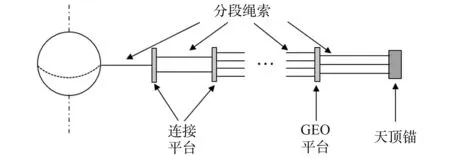
图3 分段式天梯结构示意图[21]Fig.3 Schematic diagram of segmental space elevator[21]

研究人员提出了一系列不同的天梯系统设计方案,以提高天梯运行的能耗、稳定性等方面的性能。 2009 年,Golubovi＇c 等[22]提出了一种旋转天梯(RSE)的概念。 不需要内部发动机或推进器即可将沿着RSE 弦滑动的物体从地球表面运送到外太空。 在此基础上,对RSE 进行了较详细的力学研究[23-25],这种结构的缺点在于绳索之间容易发生接触而导致故障。

2021 年,Okino 等[26]提出了一种新型的配重式天梯装置。 该系统类似地面电梯,由2 根缆绳组成:一根导缆承受着施加在结构上的张力,即常规天梯的绳索,另一根移动的缆绳连接着2 个贡多拉分别向上和向下运动。 通过数值计算对配重式天梯的性能进行了分析。 Li 等[27]提出了一种新型的多攀绳环系索运输系统的概念(L-TTS),用于有效载荷的高效运输。 如图4 所示,它由2个平行的系绳运输系统或部分天梯组成,每个系绳都有多个攀爬者。 它将减少系统的整体振动,但是在载荷运输过程中存在系绳碰撞的风险。 在此基础上,该团队又提出了一种新型环形绳架运输系统(L-TTS-R)。 在这个新概念中,除了L-TTS中提到的组件外,系统还包括几个平行的刚性环,它们均匀地固定在2 根系绳上,以保持2 个连接点的距离不变,评估了梯级对系统振动抑制、攀登者碰撞风险规避、平台相对振荡和俯仰运动以及系绳张力的影响[28]。

图4 多攀绳环系索运输系统(L-TTS)原理图[27]Fig.4 Schematic of proposed L-TTS[27]

研究人员对天梯的建造方法进行了一定研究,Takeichi[29]研究了天梯系绳展开过程中的控制问题;Yamagiwa 等[30]提出了一种建造空间升降梯的新方法,即在保持对地同步的情况下,从主空间站同时展开向上和向下的缆绳,并保持两根缆绳的平衡,该方法可以节省1/3 的推进剂质量。

在天梯能耗方面,杨小东等[31]分析了天梯攀爬器的运行环境及其受力,建立了攀爬器运行的能耗模型,由此得到了地球天梯攀爬器爬升过程总能耗;徐志良等[32]基于天梯系统动力学模型近似计算了天梯海上平台偏移范围,发现海上平台偏移变化范围与海上平台质量和绳索几何参数有关,因此可以选取合适的参数以减小海上平台的偏移;Woo 等[33]对PSE 进行了能量计算,发现与传统的火箭发射相比,5000 km 以上的距离可节省大量的能源,并研究了天梯主要参数的影响。

除此之外,杨帆[34]对履式传动的天梯攀爬器系统太空舱进行了概念设计;李宇铭[35]基于模块化设计概念给出了天梯海基平台的概念设计方案,为未来的天梯系统设计;Peet[36]研究了三层天梯发射系统的设计,并对利用这种设计的航天器的轨道力学进行了详细的数学分析。

天梯的设计对天梯的应用至关重要,通过更加合理的设计可以从最初的环节减轻天梯的静力学、动力学及能耗等方面的问题,需要深入研究。

4 天梯系统绳索受力的计算研究

4.1 静力学计算

天梯绳索的静力学计算相对来说较为简单,早在1975 年,Pearson[37]基于微分方程建立绳索单元的连续静力学模型,推导了绳索截面积渐变函数模型,但是在模型中并未考虑绳索的弹性;2007 年,Aravind[17]建立了天梯系统绳索的受力平衡方程,而Cohen 等[19]在此基础上推导了使绳索内部应力随高度不变的变截面天梯截面积表达式,并且给出了绳索、天顶锚的质量等参数的计算公式;张普卓等[38]给出了确定天梯系统结构参数及运载能力的设计流程,并且基于天梯受力平衡方程分析了天梯系统主要参数之间的关系。

天梯系统在运行过程中的受力还要受到攀爬器的影响。 2015 年,Cohen 等[39]推导了当攀爬器存在时绳索的受力平衡方程,并由此计算了攀爬器在不同高度情况下绳索的受力和变形情况。

总得来说,针对不同的天梯设计,尽管静力学计算的算法不同,但是目前都有办法较好地解决,在此基础上可以根据绳索应力实现对天梯设计方案优劣的评估。

4.2 动力学计算

天梯绳索的动力学计算需要考虑多种外部载荷、变形随时间的变化,绳索会发生与时间相关的弯曲变形,尤其对于变截面天梯,其动力学计算会变得很复杂,因此在这方面的研究往往需要做各种简化。 目前常见的天梯系统绳索动力学模型包括3 类。

4.2.1 直杆模型

在有些研究中,忽略绳索的弯曲变形,将绳索假设为一根直杆,这样可以大大简化计算,见图5。 最简单的直杆模型是刚性直杆,即在直杆模型基础上同时忽略绳索的轴向变形,假设绳索是刚体。 2009 年,Cohen 等[40]基于刚性直杆假设建立了海上赤道天梯上攀爬器运动时的动力学模型;Williams[41]在此基础上通过优化方法得到了使绳索摆振最小的攀爬器运行速度,有效减小了绳索在攀爬器造成的面内摆振;Sadov 等[42]利用超长柔性不可伸长索模型研究了天梯绳索在平衡垂直位置附近的小横向振动,分析了其本征频率特征。该模型可以认为是刚性直杆模型的改进。

图5 直杆模型示意图Fig.5 Schematic of rigid rod model

若考虑直杆模型的轴向变形,则是弹性直杆模型。 2006 年,Williams[43]在刚性杆假设基础上考虑了杆的轴向变形,研究了绳索的振动问题;涂剑平[44]用轴向运动两边简支、两边自由运动板建立了太空带状释放绳索的动力学模型;Wen 等[45]也基于弹性直杆模型研究了天梯绳索的振动及控制问题。 另外,2018 年,Hu 等[46]基于弹性杆模型研究了绳系卫星平台系统与太阳能帆板之间耦合后的动力学问题。

4.2.2 离散绳索模型

直杆模型忽略了天梯系统绳索的弯曲变形,不适合用来研究绳索的波动问题。 因此提出了离散绳索模型,将绳索进行离散化,较常见的有链杆模型和珠点模型2 类。

链杆模型是将绳索离散成一系列的杆,每2个杆之间由铰链连接,通过每个杆的转动可以模拟整个绳索的弯曲变形,而根据实际情况可以假设杆是刚性的[41,47-50]或者是弹性的[51-52]。

珠点模型是将绳索离散成一系列的质点,这些质点由弹簧和阻尼器连接,如图6 所示。 2009年,Williams[53]建立了天梯绳索的珠点模型,由此研究了天梯的振动问题,并且分析了攀爬器速度和质量对绳索振动的影响;Aslanov 等[54]基于珠点模型研究了空间升降梯与太空碎片碰撞时绳系断裂后的动力学问题;Knudsen 等[25]在研究其提出的旋转天梯上攀爬器的动力学问题时也采用了珠点模型;Ishikawa 等[55]研究了一个上行攀爬器和一个下行攀爬器同时运行时绳索的振动状态,发现这种情况下绳索的倾斜度可以降低近10 倍。

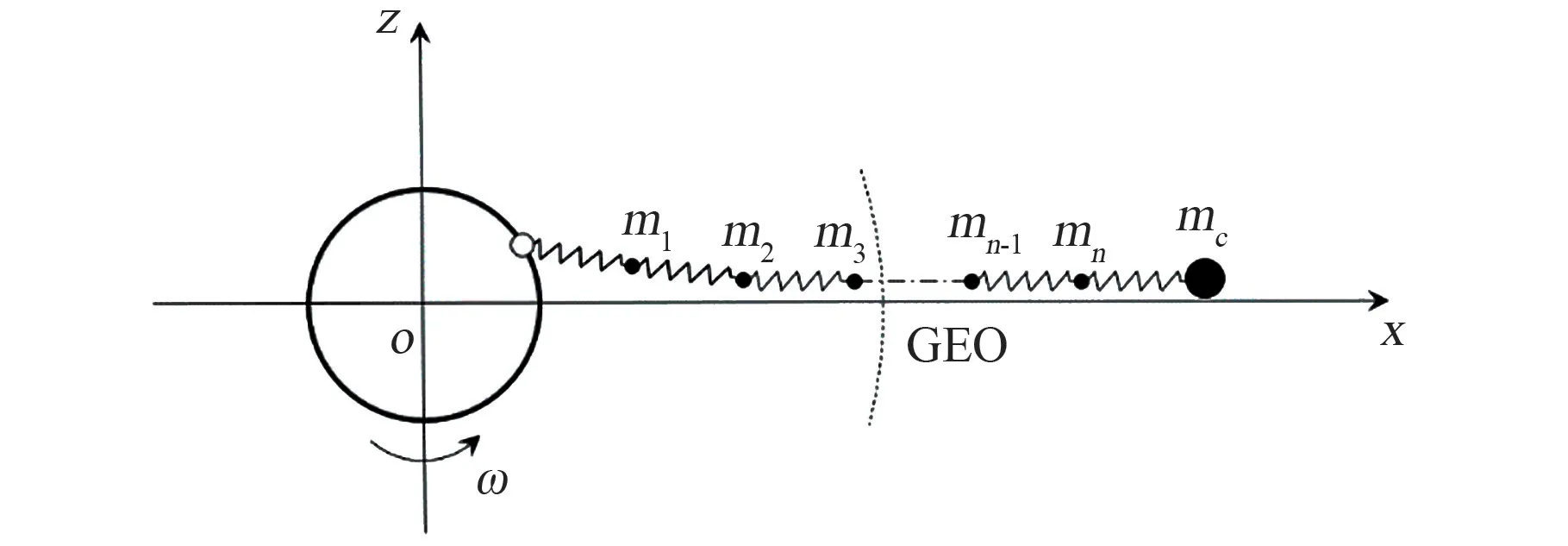
图6 珠点模型示意图Fig.6 Diagram of the bead model

4.2.3 连续体模型

对天梯绳索做离散化本质上是一种近似的思想,而更精确的方法是给出整个天梯绳索的受力微分方程或方程组并进行求解。 尽管一般在求解过程中仍然需要对方程进行一定的离散化处理,但是可以获得更高的求解精度。 2006 年,Krupa等[56]针对绳系卫星建立了微分方程组,由此对其相应的动力学问题进行了研究;Ellis 等[57]建立了绳系系统的动力学微分方程,并对其进行了离散化求解。 有限单元法的思想在微分方程的离散化求解中往往是有效的。 Li 等[58-59]采用有限元法对绳系系统的微分方程进行离散化求解,进而进行了一系列的动力学研究;2019 年,Shi 等[60]基于变长节点位置有限元方法对部分天梯(PSE)进行了动力学建模,并验证了该模型的有效性;2021年,Luo 等[61]基于绝对节点坐标公式(ANCF)对天梯系统的动力学问题进行了分析,发现该方法可以用较少的单元数来达到相同的计算精度,而且有较快的收敛速度。

天梯系统绳索的动力学计算是天梯振动模态及振动控制研究的重要基础,尽管连续体模型在建立运动微分方程组的过程中没有经过简化近似,但是由于方程组的复杂性,难以获得解析解,需要在求解过程中进行离散化,从而引入了误差。因此在天梯系统的动力学计算中如何尽可能提高计算精度仍然是未来研究的重点内容之一。

5 天梯系统绳索的振动及减振研究

天梯绳索尺度大,运行环境复杂,由各种因素产生的振动可能对天梯系统的运行造成严重影响,危害天梯系统的可靠性和安全性。 因此近年来在动力学计算的基础上,天梯绳索的振动问题受到广泛的关注。

5.1 振动特征研究

振动特征的研究是振动控制的基础,因此有很多天梯绳索振动特征的研究。 Williams[53]基于珠点模型研究了攀爬器运动过程中引起的绳索振动特征,分别建立了绳索振动过程中的动力学和运动学模型,在此基础上分别进行了模态分析;涂剑平[44]基于自由运动板模型研究了绳索振动的固有频率;2014 年,土井等[62]对天梯绳索在多攀爬器运动情况下的振动响应进行了研究;Li 等[63]在任意拉格朗日-欧拉描述的框架下,用节点位置有限元方法研究了多攀爬器系绳输送系统的动力学问题,发现所建立的弹柔系缆模型能够捕捉到系绳系统的高频振荡;Hu 等[64]研究了超大超柔性阻尼空间结构的振动问题,考虑结构振动、姿态动力学和轨道动力学之间的耦合,研究了4 个特殊弹簧的空间柔性阻尼板的振动特性和波的传播特性。

除此之外,也可以通过等比例缩小的实验进行振动研究。 2020 年,Yoon 等[65]建立了考虑系索初始张力的比例实验模型,通过实验研究了超材料的带隙特性,测量了超材料在带隙中的变形形状。

5.2 振动控制研究

天梯系统在运行过程中除了重力和离心力以外,还可能受到攀爬器运动产生的科氏力、风力、月球和太阳的引力、太阳光压、电磁力及温度影响等多种复杂荷载。 如何抑制各种荷载产生的绳索振动就成为了天梯系统研究的重中之重,因此在天梯振动方面更多的是在振动特征研究的基础上进行减振研究。

目前多数相关研究集中在如何抑制攀爬器运动对天梯绳索产生的扰动。 最直接而且简单的方法是通过控制攀爬器的运动来抑制绳索振动。2010 年,Williams[41]给出了使绳索摆振最小的攀爬器运行速度以减小绳索在攀爬器造成的面内摆振;Ishikawa 等[55]提出令2 个攀爬器同时运行,一个上行,一个下行,以抵消单个攀爬器产生的扰动,使得绳索受扰动产生的倾斜度约为单个攀爬器的1/10;王振坤等[66]研究了攀爬器加速和减速时间对绳索振动的影响,引入加速时间比和减速时间比的概念,发现通过优化这2 个参数可以有效抑制绳索的振动,并且提高系统运行效率;在PSE 的振动方面,Shi 等[67]发现在不同攀爬器个数的情况下通过调节攀爬器的运行速度控制振动角的大小,随后还研究了通过控制攀爬器对平行部分天梯系统(PPSE)的振动抑制问题[68]。

主动控制方法往往具有更高的效率,目前也有较多的研究。 Malashin 等[69]利用Lyapunov 方法,得到了空间系绳系统边界控制问题的解析解,并通过横向位移控制和端部张力控制实现了边界控制,通过数值模拟验证了所提出的控制机制的有效性。 在电动力系绳系统中系绳的振动包含扭转变形,Kojima 等[70]提出使用智能薄膜传感器和致动器来感知和控制系绳的振动,计算结果表明,基于直接速度反馈控制(DVFC) 可以减小带绳的弯曲振动和扭转振动;Tragesser 等[71]给出系绳系统空气制动的一个控制方案估算,该方案减少了计算时间,并增加了算法的鲁棒性;Shi 等[72]通过对攀登者施加力矩控制来抑制PSE 的振动,在此之后,又提出了一种新型的混合控制方案使存在未知系绳张力的PSE 在运送货物中稳定[73]。

对于除攀爬器以外的荷载对天梯绳索扰动产生的振动问题,目前研究仍然较少。 2020 年,Otsuka 等[74]在假定系绳杨氏模量与系绳温度有关的前提下,分析了考虑绳索温度变化的天梯绳索振动特征。 结果表明,绳索在南北方向无振动,但在东西方向有振动。 通过分析固有频率发现应提高绳索的内应力或缩短绳索长度,使其固有频率移至较高的一侧以抑制振动。

天梯尺度和质量都较大,造成天梯的振动频率往往较低,而低频振动的能量更难以耗散。 因此天梯系统的振动控制是目前天梯研究的热点问题,仍然有必要在被动和主动控制方面进一步深入研究,未来在高精度振动计算的基础上,可以考虑通过合理的设计,将被动控制和主动控制相结合,实现天梯振动的高精度控制。

6 总结与展望

本文主要针对地球赤道天梯的研究进行了综述,得到以下结论:

1)天梯绳索的静力学问题主要是尽可能降低绳索的拉应力,通过改进天梯的设计,可以实现天梯绳索拉应力的大幅度减小;

2)目前天梯的动力学计算可以通过简化模型或连续体模型获得较好的精度,但是提高精度意味着计算量的增加;

3)天梯绳索的动力学问题主要是各种荷载造成的振动控制问题,通过调整天梯的设计及攀爬器的数量和速度可以一定程度上对振动进行抑制,而主动控制的效率仍然有待提升。

过去限制天梯发展的最主要因素是天梯绳索需要承受极高的应力,远超过钢等普通材料的抗拉强度。 这一问题在近年来碳纳米管和石墨烯的快速发展之后有望得到解决。 除了绳索材料的研究以外,对于天梯本身的研究,目前仍需关注的问题如下:

1)更合理的天梯系统结构设计。 已经有人提出了各种天梯系统的结构设计方案,但是仍需要更深入的研究,使天梯在低工作应力、低能耗、高运载能力、高稳定性、多用途性以及安全性等方面获得平衡。

2)更详细的动力学研究。 目前已有很多针对天梯动力学的研究,尤其是振动控制方面受到较多关注。 但是还需要寻求对天梯可能出现的各种振动问题的最佳处理方法,尤其是这方面的研究与天梯的结构设计密切相关,不同的天梯结构对应的最佳振动抑制方式可能不同。

3)近地轨道以下范围扰动的抑制。 目前有关天梯振动控制方面的多数研究都集中在如何抑制攀爬器造成的扰动。 实际上天梯可能会遇到多种类型的扰动,绝大多数是在近地轨道以下范围,尤其是太空碎片以及大气层内的风、雨、雷电等都对天梯有明显的影响。 到目前为止,对于近地轨道以下范围扰动的研究仍然较少,有待更广泛深入的研究。