基于水动力-力学耦合的海绵城市渗蓄水风险预测

陈冬琴

（长江职业学院，湖北武汉 430074）

海绵城市概念提出至今，研究主要集中在“低影响开发”、实现雨水控制目标，如渗、滞、净、蓄、用、排等多个方面。很多城市在海绵城市建设中，缺少对地质环境研究，对场地环境不了解，海绵城市技术适用性不明确，导致出现很多地质环境问题，如地面沉降、开裂、特殊土层膨胀等。海绵城市建设应从自然水文条件角度出发，开展城市地质调查工作，分析海绵城市功能与环境地质适宜性的基础上进行规划设计，实现自然积存、自然渗透、自然净化的功能。本文以某城市规划区为研究对象，采用GMS软件（表水及地下水耦合）计算地下水流场结合Terzaghi固结理论，进行水动力学-力学耦合数值模拟，模拟计算海绵城市渗蓄水时，对地下水位的影响，预测海绵城市渗蓄水对地质环境地面沉降量的影响。

1 透水铺张层及地质条件

本次研究透水铺装层采用透水混凝土、级配碎石层、级配砾石层，共同特点是孔隙率高，具有很好的渗蓄水能力。下垫层地质条件为：上部为粉砂土、全新统中期冲积物。中部为细砂土，分布于西南、西北部，一般顶板埋深1~1.5m；下部粉质黏土，顶板埋深1~2m，厚度15~20m；底部为黏土，具水平微层理。

2 数学模型

2.1 地下水流动数学模型

根据Darcy定律和水均衡原理，忽略密度变化对地下水影响的三维流动数学模型为：

式中：Kxx、Kyy、Kzz分别为沿主方向的渗透系数[L/T]；h(x,y,z,t)为水位[L]；w为单位体积单位时间内注入或抽出的水量[1/t]；为时间[T]；μs为单位储水系数[1/L]；h0(x,y,z)为流场初始水位[L]；B1为一类边界条件；B2为二类边界条件；q(x,y,z,t)单位面积已知流量（l/t）。

2.2 地面沉降与地下水耦合模型

储水系数的定义是当水位下降一个单位时，从空隙介质中释放的水量（体积），空隙介质被压缩，从空隙介质中释放的水量储水系数表达式为：

式中：γw为水的重度[M/（L*T）2]；为储水系数[1/L]；n为孔隙度[-]；βw为水的体积压缩系数[LT2/M]；α为土体体积压缩系数[LT2/M]，表示为：

根据有效应力原理，变形只考虑垂向方向，可以把地面沉降和地下水水位耦合起来：

式中：Em为压缩模量[M/LT2]；b为厚度[L]。

式中：Δε为应变增量；Δσ为应力增量[M/（L*S2）]；Ee和Ev为弹性压缩模量和塑性压缩模量[M/（LS2）]。

3 数值模型构建

3.1 研究区地质结构概念模型的构建

选择某城区海绵城市进行数值模拟如图1所示，根据该区上层透水铺张、下层水文地质条件，对模拟区模型进行概化，该模型分为5层，总厚度30m，透水铺张层根据人工碎石粒径不同分为3层，第一层透水铺张层厚度0.3m；第二层透水铺张层厚度0.25m；第三层透水铺张层厚0.25m，如表1所示，共0.8m。下部地质条件为：上层粉砂土，一般厚度为5~10m；中部细砂土，厚度5~10m；下部粉质黏土，具水平微层理，5~10m；底部为黏土层。

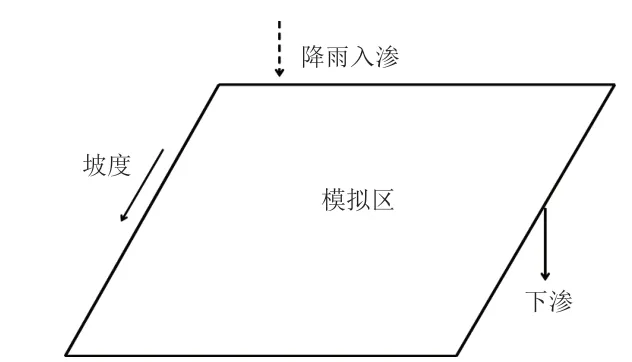
图1 研究区概念模型

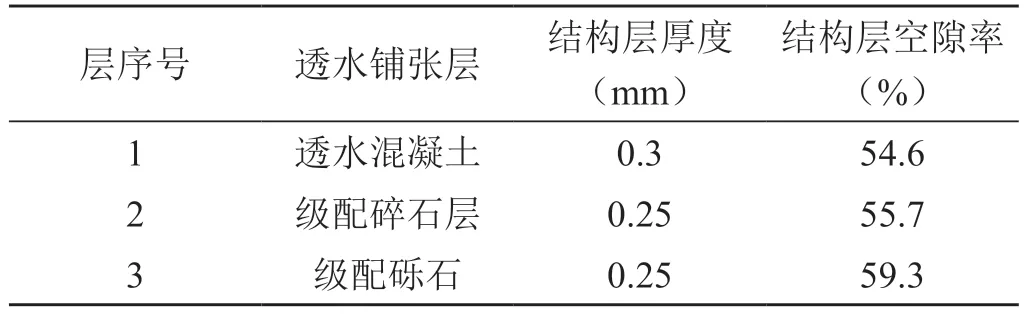
表1 透水铺装层填料情况

3.2 模型参数取值

3.2.1 参数基础值选取

模型网格剖分平面上的网格间距为100m×100m，根据地层情况确定垂直方向的间距。

透水铺张层的水文地质参数根据室内实验确定，模拟区初始水位根据2016年3月各层监测孔观测水位确定，模拟边界根据模拟区1 000m附近的监测孔观测水位给定。地面沉降模拟应力期2016年10月到2020年11月，时间间距为1个月。根据分析计算或是工程地质分析时钻孔中的土样测试数据确定各层土体的各类初始参数。

3.2.2 模型识别

模型识别是通过反复调整参数，提高数值模型的精度，使模型的计算结果接近实际值。本次计算的主要参数是渗透系数、储水系数、压缩模量等。模型识别的初始流场选用2016年10月的统测水位，拟合检验以2018年7月的流场、变形监测数据为依据，调整参数得识别后的土体参数见表2。

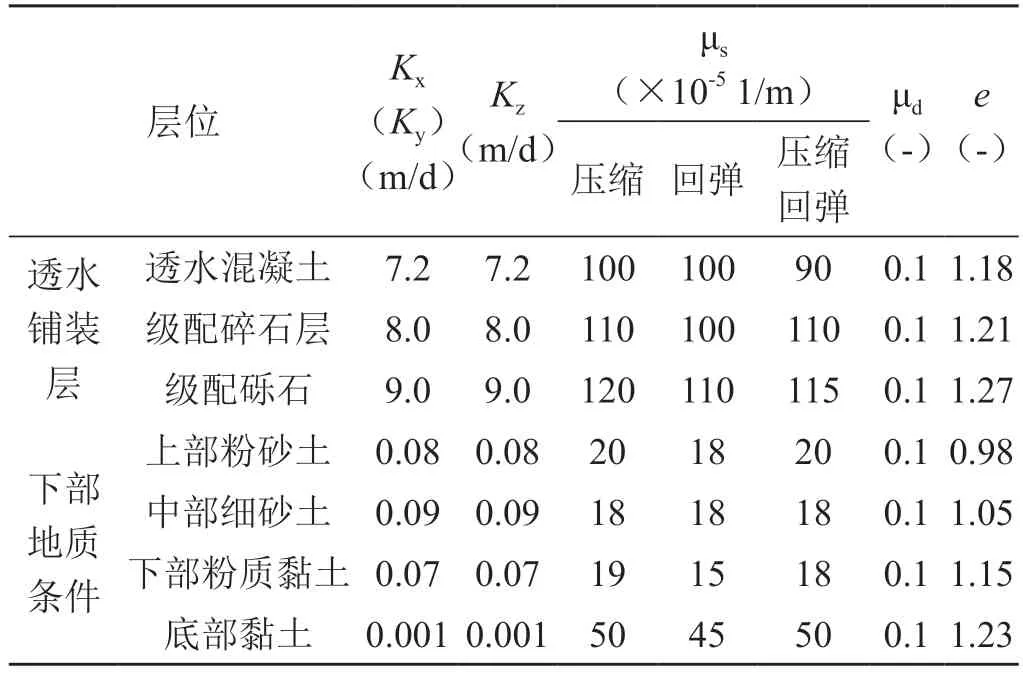
表2 识别后的各层土体参数表

3.3.3 海绵城市渗蓄水风险数值模拟

此次用于海绵城市渗蓄水风险数值模拟的预测方法是基于Terzaghi固结理论和GMS软件建立。模拟海绵城市不同降雨强度及降雨历时、地下水主位补给量、地面沉降度。

根据模拟区的降雨特征，丰水期是7月份，基于7月份流场，通过改变降雨入渗补给量，模拟3种降雨模式（表3），计算土压力的变化值，分析降雨对海绵城市渗蓄水风险的影响如表4所示。

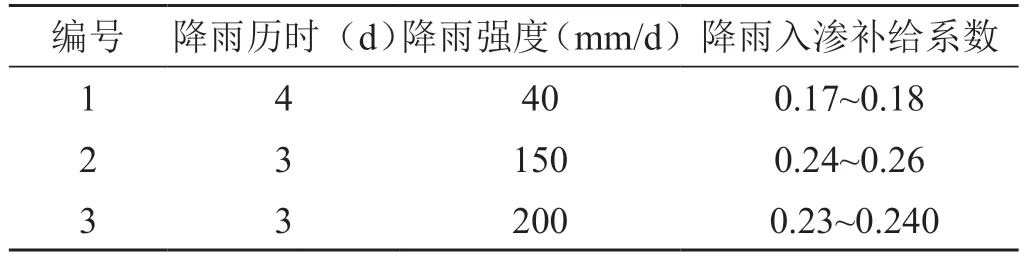
表3 3种降雨预测模式

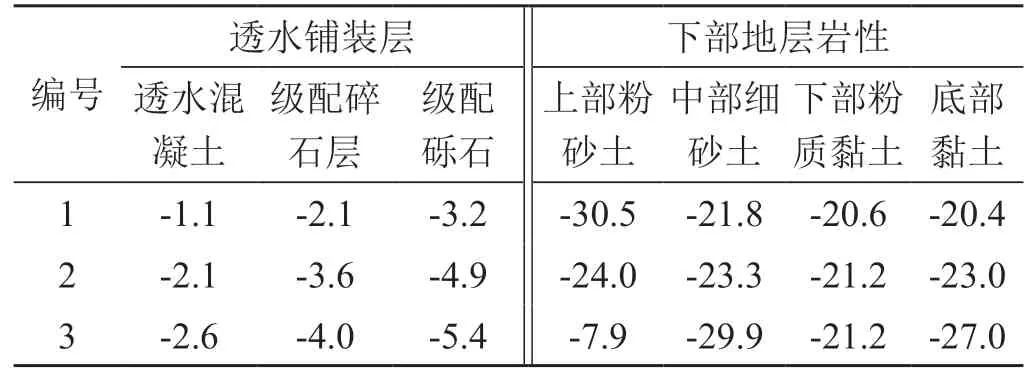
表4 各层土体沉降比重统计表 单位：%

模拟海绵城市渗水所产生的沉降值。透水铺张层在饱水情况下，表3中不同的3种降水模式释放水量到蓄水之前的潜水面，土体沉降的变化值如表5所示。模拟海绵城市渗蓄水交替3次，所产生的沉降值如表6所示。

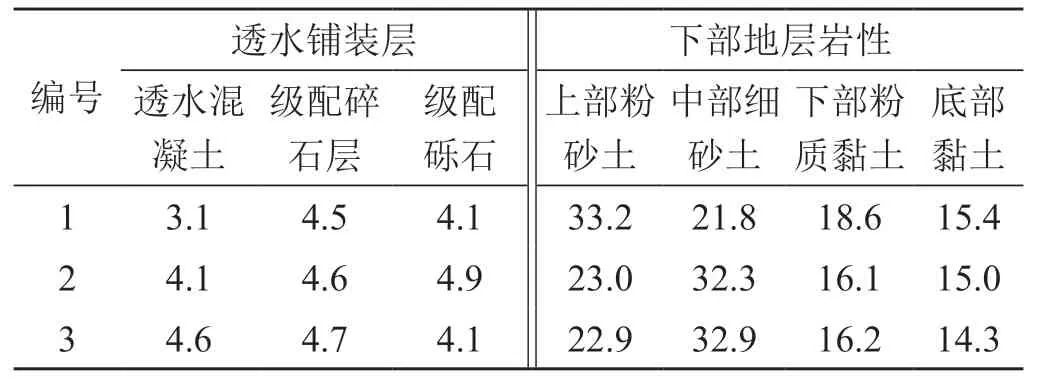
表5 各层土体沉降比重统计表 单位：%

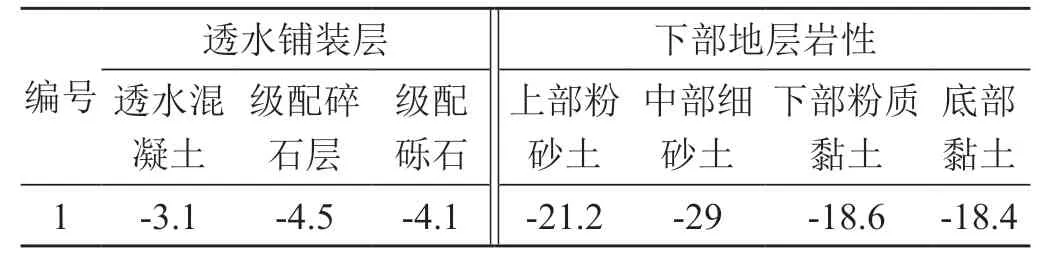
表6 各层土体沉降比重统计表 单位：%

4 模拟结论分析

在GMS软件计算地下水流场的基础上，采用水动力-力学耦合模型，以海绵城市的渗蓄性对地下水动态的影响，模拟计算了土体沉降值，具体结论如下。

1）在模拟降雨情况下，海绵体在蓄水状态时土体呈现上浮状态。降雨量小，降雨历时长时，下部地层的上部粉砂土变形值最大达到 30.5%；当降雨历时增大，强度增强时，中部细砂土变形值最大达到29.9%。

2）海绵城市渗水时，释放水量回到蓄水之前的潜水面，土体呈压缩状态。下层土体的变化值都较大，中部细砂土变形值最大达到 32.9%。

3）海绵城市在历经渗蓄水交替3次，整个铺张层及下层土体都发生了较大沉降，在渗蓄水频繁交替时对土体的破坏力最大，其中沉降最大的是中部细砂层达29%。

以上研究表明，透水铺张层和下垫层一定要考虑到渗蓄水的风险性，必须经过预测与评价使沉降值控制在不产生破坏的范围内。下垫层的土体不符合海绵体渗蓄水功能性要求时，需采取措施加固。