基于PSO的船舶分段制造流水线生产平衡策略研究

王荣凯

（上海华润大东船务工程有限公司，上海 202155）

船舶制造业的发展状况是体现国家经济、科技实力的重要标志之一，随着全球竞争加剧，现代化造船模式是增强市场占有率的有效途径[1-2]。自主研发能力不足、生产效率低等问题严重阻碍我国造船业进一步发展，在船舶制造过程中，生产线的平衡问题是制约生产效率的核心问题之一[3-4]。船舶分段制造工艺依据形状的不同，分为平面分段与曲面分段。曲面分段结构相似性不强，国内企业普遍使用固定工位的生产方式，存在组织调度混乱、生产周期长问题，严重制约船舶制造水平的提升[5]。研究以船舶曲面分段制造车间的生产流程为分析对象，构建生产周期最短的加工模型，利用混合启发式PSO 算法解决调度问题，实现生产效率最大化。

1 基于混合启发式PSO 的曲面加工流水线平衡模型构建

1.1 曲面分段加工流水线平衡模型构建

在船舶曲面分段加工中，一些国际企业使用流水线模式生产，但该方法设备成本高、加工工艺严格，不适合我国船舶制造。曲面分段加工的相似性不高，但面对批量的船舶制造时，各曲面分段结构的相似性明显增强。同时各分段结构加工工艺基本包括焊接、装配等主要作业流程，且各工艺要求的相似度较高，研究流水线与固定工位生产模式相结合，在固定曲面加工工位上实现高效流水作业，提高船舶曲面分段生产效率。其曲面分段加工流程如图1所示，根据加工工序、作业人员及设备工具划分作业小组，各小组以一定的顺序在分段结构之间流动作业，完成各分段加工工序任务。

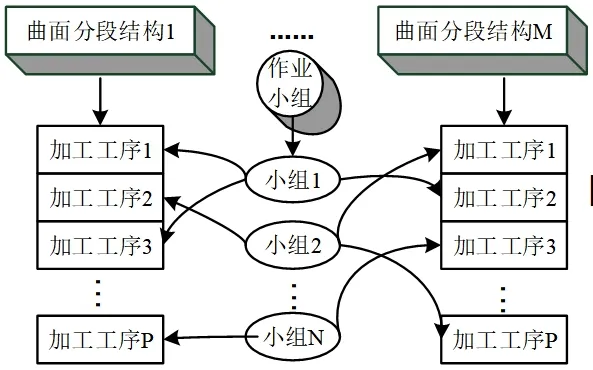
图1 曲面分段加工流水线示意图

固定工位与流水线相结合的生产模式下，每个待加工曲面分段的制造由不同小组完成，每个小组在不同的曲面分段之间进行类似操作，形成一种类似流水线的生产模式。这种模式在空间上，因其加工的结构位置固定不变，属于固定工位生产模式，但在逻辑层面上，该曲面结构是被不同作业人员、设备流动而完成加工，属于流水线生产方式。这种混合流水线的加工模式与其他独立加工模式相比，可以通过组织人员、设备的流动，而减少因分段结构流动而带来的运输成本。同时可以采用加强作业人员的加工管理，严格把握生产过程，以保证分段结构的加工质量和加工周期。

混合加工流水线可以在不改变当前的生产能力、生产手段的基础上，通过改变组织生产方式，以达到制造多种产品的需求。在曲面分段加工过程中，每个分段结构的工序是不变的，根据各小组的加工能力选择待加工工序，同时协调调度不同曲面分段结构之间的小组流水加工顺序，是缩短加工周期的关键。同时根据工序所需时间，进行恰当的分解和合并，使得各个工序的作业时间趋于一致，保证每个小组的加工时间相等、均衡生产，实现作业小组在各个工序间的高效工作。已知小组的工作能力W 和分段结构的工作总量，忽略设备和工具故障问题。设某生产车间有待加工的分段结构M{1,2,…,m}个，加工工序有P{P1,P2,…,Pm}，作业小组有N{1,2,… ,n}个，作业小组会按照工序的不同划分成几种不同类型的小组，整个车间调度目标函数为最大加工时间最小值，即f(x)=minTmax。在加工流程中，当Oikq=1 时，表示第i个分段结构第k 工序选择q作业小组。对小组加工的工序和资源进行约束，同一曲面分段的不同工序不能在同一时刻一起加工，且一个小组只能加工某分段结构的一个工序。每个工序一旦开始，直至完成本工序才能结束；前一个工序完成后才能进行下一道工序，每个工序必须按照顺序加工。当所有工序完成后，曲面分段的总加工时间不能小于单个结构加工时间，即时间约束Tmax≥Tikq。

1.2 混合启发式PSO 算法

船体结构中曲面分段占比较大，对曲面分段加工流水线调度进行优化是实现生产效率最大化的关键。粒子群优化算法（Particle Swarm Optimization Algorithm,PSO）因概念简单、容易实现、收敛性较好等优点被广泛应用在众多领域。PSO 是模拟鸟类寻求食物的群体行为的算法，其核心思想是通过不断迭代更新种群位置进而搜索得到全局最佳。假设在 维搜索空间内，存在一群初始粒子，根据相关信息粒子的速度更新公式如式（1）。

式（1）中，Vxy(t)是第t 次迭代时粒子x在y维上的速度分量，δ表示惯性系数，R1,R2分别是[0,1]范围内的随机数，C1,C2是粒子的认知系数，Mxy(t)代表第t次迭代时粒子x在y维上的位置分量，Pbxy（t）代表第t次迭代时个体最优粒子在y维上的位置分量，Gbxy（t）表示第t次迭代时全局最优粒子y维上的位置分量。为了保证PSO 算法性能较好，需要限制粒子的速度范围和位置范围，分别是Vminy≤Vxy(t+ 1)≤Vmaxy和，其中Vminy、Vmaxy分别代表搜索空间内y维上的速度下界和上界，Mminy、Mmaxy分别代表搜索空间内y维的位置下界和上界。限制范围后，粒子的位置更新表达式为式（2）。

利用PSO求解时，根据方案确定可行解和评价函数，在搜索空间内随机生成粒子，计算各粒子的适应值、局部最优及全局最优粒子位置；根据式（1）和式（2）更新粒子速度和位置，计算粒子适应值，得到局部最优位置，比较后获得全局最佳位置及适应值。从PSO 求解过程中可以看到粒子的位置变化是通过局部最优以及全局最优的位置进行更新，在一定程度上反映了种群的多样性。且粒子的位置仅会在最优粒子发生变化时进而有所改变，这说明PSO 算法具有一定的稳定性和适应性。

PSO 算法对于初始参数的依赖性较强，同时在解决曲面分段加工调度问题时，速度难以表达，因此引入遗传算法和模拟退火优化算法与之结合，得到混合启发式PSO 算法。将δVxy(t)和C1R1(Pbxy(t)−Mxy(t))+C2R2(Gbxy(t)−Mxy(t))分别视作遗传算法的变异、交叉操作。经过遗传算法的交叉、变异操作后，粒子的最优解存在比原有解更差的情况，采用模拟退火思想，准许目标函数在一定范围内变差。计算粒子适应值，得到局部最优位置，比较后获得全局最佳位置及适应值，混合启发式PSO 算法的求解流程见图2。

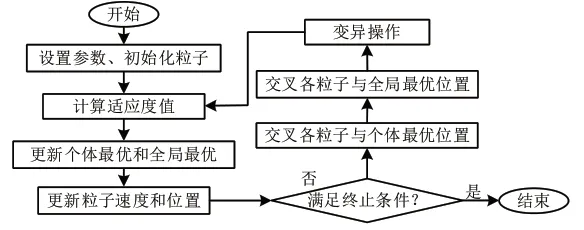
图2 混合启发式PSO 求解流程

2 结果数据分析

2.1 混合启发式PSO 算法性能分析

为了验证调度优化中混合启发式PSO算法的性能，研究与原始PSO 算法、遗传算法以及模拟退火算法作对比。使用两种实验测试函数测试四种算法的收敛性，四种算法在测试函数上的收敛性曲线见图3。

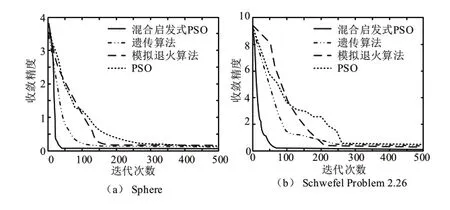
图3 四种算法的收敛曲线

在图3中可以看出，四种算法在不同测试函数中的收敛速度有所差异。在两种测试函数中，PSO 和模拟退火算法收敛速度最慢，最小收敛值分别为0.167 和0.183。遗传算法的收敛速度较快，收敛值最小值为0.148。混合启发式算法的收敛速度最快，其最小值0.09。说明研究的算法收敛性能最优，优化效率最高。为分析几种算法模型求解结果的有效性，绘制的PR 曲线见图4。

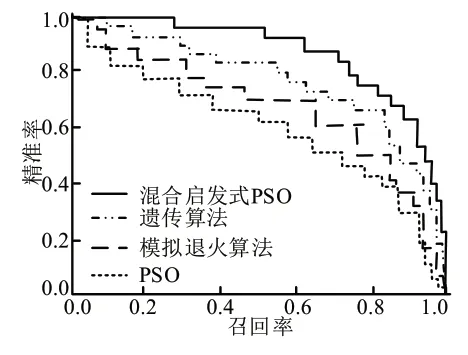
图4 四种算法的PR 曲线

从图4的PR 曲线可知，混合启发式PSO 算法得到的优化结果表现最优，四种算法的PR 曲线包含面积分别为0.923、0.843、0.766、0.695，其计算结果说明PSO算法对模型求解的性能最优，求解结果具有较高的参考价值。

2.2 曲面分段制造生产平衡策略效果验证

研究以某船舶企业曲面分段加工车间为案例，选取8 个待加工曲面分段，每个分段主要有焊接和组装工序。根据车间相关数据构建曲面分段加工调度模型，以最短加工周期为目标，利用混合启发式PSO 算法进行调度策略求解，可得到曲面分段作业小组的生产安排表，其绘制的曲面分段加工调度甘特图如图5所示。

图5 曲面分段加工调度甘特图

从图5可知，由混合启发式PSO 算法优化调度得到的总共加工时间为77.9h，该车间的实际生产时间为95h，生产周期缩短了18%。说明使用基于改进PSO 的曲面分段调度策略可以有效提高车间的生产效率，缩短生产周期。

3 结论

面对当前船舶制造企业中存在的生产效率低等问题，研究将流水线与曲面分段固定加工相结合，建立最短生产周期的流水线生产模型，并利用混合启发式PSO算法实现生产调度。性能分析结果显示，改进PSO 算法收敛性最佳，模型求解结果具有较高的参考价值。实例分析结果显示，利用改进PSO 得到的曲面分段加工调度策略与实际生产数据相比，生产周期缩短了18%。说明研究的生产策略可以有效提升船舶的制造效率，降低生产成本，提高企业竞争力。