Real-time observation of soliton pulsation in net normal-dispersion dissipative soliton fiber laser
Xu-De Wang(汪徐德) Xu Geng(耿旭) Jie-Yu Pan(潘婕妤) Meng-Qiu Sun(孙梦秋)Meng-Xiang Lu(陆梦想) Kai-Xin Li(李凯芯) and Su-Wen Li(李素文)
1School of Physics and Electronic Information,Huaibei Normal University,Huaibei 235000,China
2Anhui Province Key Laboratory of Pollutant Sensitive Materials and Environmental Remediation,Huaibei Normal University,Huaibei 235000,China
Keywords: fiber laser,soliton pulsation,soliton molecule,dispersive Fourier transformation
1.Introduction
As an ideal experimental platform, fiber lasers have the capacity to produce ultrashort pulses which could find important applications in the fields ranging from fundamental physics to industrial purposes.[1]Using the passive modelocking techniques, various exotic soliton phenomena can be experimentally observed in fiber lasers, such as conventional soliton,[2]dissipative soliton (DS),[3]vector soliton,[4]dark soliton,[5]and polarization domain wall soliton.[6]In particular,DSs exist in nonconservative dissipative systems,in which the additional balance between gain and loss is crucial in the formation of DSs.[7]The DSs exhibit complex dynamic behaviors;therefore,they can unveil the underlying physics and mechanisms of soliton dynamics.
Over the past decade,parameter-invariant stationary DSs have been widely investigated in fiber lasers.However,under a certain parameter condition,solitons operate in nonstationary state and exhibit complex nonlinear transient dynamics,which are difficult to detect by time-averaged measurement apparatuses.In recent years,a novel real-time measurement method,called dispersive Fourier transform (DFT) technique, allows the characterization of the transient dynamics of DSs.[8,9]Through time-stretch method, the pulse spectrum can be mapped into a temporal waveform to obtain the real-time spectral information.Hence,utilizing DFT,various complex ultrafast nonlinear phenomena, such as soliton explosions,[10-12]soliton pulsations,[13,14]and soliton buildup dynamics,[15-17]as well as internal motions of soliton molecule,[18-20]have been well investigated.
Recently, soliton pulsation has attracted attention as a typical nonstationary oscillating pulse structure.In contrast to the scenarios of constant-amplitude pulse train generated in fiber lasers, the amplitude of the pulsating soliton evolves periodically along with the cavity round trips.The mechanisms of the pulsating behaviors,[21]including spectral filtering, dispersion effects, nonlinear effects, slow gain dynamics, and saturable absorption, are complex.Pulsating soliton states have been theoretically predicted based on the complex Ginzburg-Landau equation.[22,23]The formation of soliton pulsation has an intrinsic nature in dissipative fiber laser,regardless of the dispersion regime.[24,25]Pulsating solitons with different properties, such as pure soliton pulsation,[26]breathing DS explosion,[27]creeping soliton,[28]and pulsating soliton with chaotic behavior,[29]have been successively investigated.In earlier studies,the pulsation process was generally identified by the pulse energy or amplitude oscillation.This pulsation state is referred to as visible soliton pulsation.In addition to the energy pulsation, several studies involving invisible soliton pulsation have been performed,[30]where the soliton pulsates in the pulse profile and the peak power but remains energy-invariable under certain parametric conditions.Benefiting from the DFT technique to acquire the shot-to-shot pulse spectrum, the real-time spectral evolution of invisible soliton pulsation can be well observed and analyzed.The investigation of soliton pulsation is important to gain an insight into laser physics, which could help optimize laser performance.In contrast to the great progress made in the study of stationary soliton dynamics in ultrafast lasers,soliton pulsation has not been thoroughly explored.In light of the diverse nonlinear dynamical phenomena involved in fiber lasers,new types of soliton pulsations,particularly invisible soliton pulsation,could be discovered by using the DFT.
In this study,the real-time evolutionary dynamics of soliton pulsation is investigated by using the DFT technique.Visible and invisible soliton pulsation are generated in the netnormal-dispersion fiber laser.The visible soliton pulsation can operate in single- and dual-soliton states, which has obvious energy oscillation.Notably,by adjusting cavity parameters,the phenomenon of invisible soliton pulsation with constant energy can be observed.The shot-to-shot spectra exhibit quasiperiodic spectral pulsation arising from periodic oscillation of the soliton inside the molecule.The experimental results could facilitate an in-depth understanding of the complex features of pulsating solitons.
2.Experimental setup
The experimental setup is shown in Fig.1.The DS is generated by using a net-normal-dispersion mode-locked fiber laser and stretched by the DFT system.In the ring laser cavity, a 4.5-m-long erbium-doped fiber with a dispersion coefficient of-18.5 ps·nm-1·km-1was used as a gain fiber and pumped by a 980-nm laser diode through a wavelengthdivision multiplexer.A 1.2-m-long dispersion-compensation fiber with a dispersion coefficient of-152.7 ps·nm-1·km-1was used to regulate the cavity dispersion.The residual fiber was a 9.9-m single mode fiber with an anomalous dispersion of 17 ps·nm-1·km-1.A fiber-based polarization-dependent isolator(PD-ISO)was used,along with two polarization controllers(PCs)that were included to achieve the nonlinear polarization rotation (NPR)-based mode-locking and ensure the unidirectional oscillation of the laser.A 90:10 optical coupler was employed to emit laser output.The total cavity length was approximately 15.6 m with a net cavity dispersion of~0.125 ps2; thus, the fiber laser operated in the net-normaldispersion regime.

Fig.1.Experimental setup of dissipative soliton all-fiber laser.LD: laser diode; WDM: wavelength-division multiplexer; EDF: erbium-doped fiber;PC: polarization controller; PD-ISO: polarization-dependent isolator; DCF:dispersion compensation fiber;OC:optical coupler;SMF:single mode fiber;PD:photodetector;OSA:optical spectrum analyzer.
In order to provide enough dispersion for DFT measurement system,a roll of SMF with a length of 26 km and the total dispersion of-572 ps2was employed to stretch the output pulses.The stretched pulses were detected by a 4-GHz oscilloscope together with a 12.5-GHz fast photodiode.Therefore,the real-time spectral resolution by DFT is~0.57 nm.The spectral information can be directly measured by the oscilloscope,thereby enabling real-time access to the soliton dynamics.
3.Results and analysis
3.1.Fundamental mode-locked dissipative soliton
Owing to the NPR effect, the stable mode-locked pulse train is achieved at pump power of~80 mW.The laser performance of the DS is depicted in Fig.2.

Fig.2.Fundamental mode-locking operation.(a) Pulse train, (b) optical spectrum recorded by OSA, (c) RF spectrum, (d) optical spectrum measured by OSA(blue curve)and DFT(red curve),(d)shot-to-shot spectra by DFT.
Figure 2(a) shows the pulse train at a pulse interval of 75.9 ns as determined by the cavity length.Figure 2(b) presents the corresponding spectrum,which has characteristically steep spectral edges in the normal-dispersion regime.The central wavelength is 1567 nm at a 3-dB bandwidth of 26.1 nm.Moreover, the radio-frequency(RF)spectrum in Fig.2(c)indicates that the laser operates at a fundamental repetition rate of 13.17 MHz with a signal-to-noise ratio of 50.9 dB.
To validate the reliability and accuracy of DFT technique, the spectrum measured by the optical spectrum analyzer(OSA)and the spectrum obtained by the DFT are compared in a linear spectrum range as shown in Fig.2(d).We can see that the average spectrum over 1000 round trips measured by the DFT (red curves) coincident well with the one measured by the OSA(blue curves).The consistency between the two spectra indicates that the DFT technique can be used to accurately measure the spectral characteristics of pulses.Notably, the fluctuation of DFT spectrum is mainly due to the low output power and measurement noise from the detection system.Figure 2(d)shows the evolution of 1000 consecutive real-time spectra.The profile of each spectrum remains nearly unchanged in the process of evolution, further indicating that the DS fiber laser can operate in a stable state.
3.2.Conventional visible soliton pulsation
By subtly adjusting the PCs,the stable mode-locking operation transforms to the soliton pulsation state at 105 mW.The spectrum of the pulsating soliton presents as arcuate at both edges,instead of the conventional steep edges,when the DS starts to pulsate[31]as shown in Fig.3(a).The ensemble average of the real-time spectra results in arcuate edges on the spectrum measured by using the OSA.Limited to the scan rate of the OSA,the spectrum remains almost unchanged with time going by.The inset of Fig.3(a) shows the pulse train of the pulsating soliton on a large time scale.The intensity modulation with a period of~22.6 µs is exerted on the pulse train.The RF spectrum has two symmetric side peaks around the main peak with a 44.21-kHz frequency difference as shown in Fig.3(b),indicating that the typical pulsating soliton is generated by the fiber laser.The frequency difference of 44.21 kHz corresponds to the period of soliton pulsation.The real-time spectral and temporal evolution dynamics of 1000 consecutive round trips are recorded by the high-speed oscilloscope as shown in Figs.3(d) and 3(e), respectively.The pulse periodically varies its energy and spectral bandwidth with time.By integrating the DFT spectrum intensity in each round trip,the energy evolution over 1000 round trips can be determined as shown in Fig.3(c),which exhibits the periodic energy oscillation for this case.The energy evolved synchronously with the spectral bandwidth breathing with a period of 298 round trips(22.6µs).
Figure 4 shows six transient spectral profiles corresponding to different round trips within a pulsating period.The realtime spectral bandwidth and amplitude continually vary with round trip.The stronger the pulsating soliton energy,the larger the real-time spectral bandwidth and amplitude are.This variation ascribes to the incomplete balance among the dispersion,nonlinearity, gain and loss within one round trip.Notably,sharp spectral peaks at the edges arising from discontinuities in the spectral phase are not observed, which is possibly attributed to the insufficient nonlinearity in the laser cavity.[32]

Fig.3.Single-soliton pulsation operation.(a)OSA spectrum,(b)RF spectrum,(c)energy evolution,(d)consecutive shot-to-shot spectra,(e)temporal evolution.

Fig.4.Transient spectral profiles within a pulsating period under single-soliton pulsation.

Fig.5.Dual-soliton pulsation operation.(a)OSA spectrum,with inset showing pulse train on a large time scale),(b)RF spectrum,(c)energy evolution,(d)consecutive shot-to-shot spectra,(e)temporal evolution.

Fig.6.Transient spectral profiles within a pulsating period under dual-soliton pulsation.
By slightly adjusting the PCs and the pump power, the fiber laser enters into the dual-soliton pulsation regime.Figure 5(a) shows the spectrum from the OSA at 115 mW.Like the single-soliton pulsation, the spectrum still has arcuate edges.The pulse train on a 100-µs time scale exhibits deeper amplitude modulation as shown in the inset of Fig.5(a).The RF spectrum is displayed in Fig.5(b).The frequency separation between multiple peaks is~65.9 kHz,which is roughly equivalent to the pulsating period of~200 round trips.Comparing with the RF spectrum in Fig.3(b),there are many subpeaks around the main peak, indicating that the dual-soliton pulsation is more stable.The periodic evolution of spectral intensity and temporal intensity are represented in Figs.5(d)and 5(e),respectively.The two solitons have the same pulsating characteristics.As shown in Fig.3, the pulsation period(~200 round trips) is shorter than the single-soliton pulsation period (~298 round trips), and the dual-soliton pulsation is stronger in both temporal domain and spectral domain.The corresponding energy evolution is depicted in Fig.5(c).Obviously, the energy oscillates periodically in a zigzag pattern.The energy modulation within each period approaches to nearly 50%.The arcuate extents of the spectral edges are related to the pulsating state experimentally.Generally, the stronger the pulsating soliton, the larger the arcuate extent of the spectral edges is.
Figure 6 shows six typical single-shot spectra within a pulsating period.Similarly, real-time spectral bandwidth and amplitude vary with round trip.Because the energy of dualsoliton pulsation is larger than that of single-soliton pulsation,the variations in bandwidth and amplitude are more obvious.In particular, the sharp spectral peak arises at the edges in the spectrum widening process, which relates to shock-wave dynamics occurring in normal-dispersion mode-locked fiber lasers.[33]
3.3.Invisible soliton pulsation
Further increasing the pump power to 150 mW and carefully adjusting the PCs,the soliton molecule is generated in the cavity,which is indicated by the modulated spectrum from the OSA shown in Fig.7(a).The modulation period is 0.73 nm,suggesting that the pulse separation inside the soliton molecule is 11.1 ps.The pulse train in Fig.7(b)operates at a fundamental repetition rate, and the pulse intensity is uniform without visible fluctuation on a large time scale.Owing to the limited bandwidth of the oscilloscope,the pulse separation is too small to be observed.Consequently, the soliton molecule appears as one pulse in the oscilloscope.Based on the results, a stable soliton molecule is generated in the fiber laser.However,with the aid of the DFT system, there occurs the distinctive phenomenon of consecutive shot-to-shot spectra exhibiting the quasiperiodic spectral pulsation.The corresponding shot-toshot spectra of 3000 round trips are plotted in Fig.7(c),where the spectra pulsate obviously with a period of approximately 410 round trips.Figure 7(d)illustrates the more detailed feature of real-time spectra from the 100th to 1100th round trip,revealing the evolution dynamics with a typical interference pattern presented in the spectrum of a soliton molecule.In the evolution process,the separation of the spectral fringe remains nearly unchanged.Constant spectral-modulation spacing implies a fixed intermolecular pulse separation in the time domain.Note that the position of spectral fringe shifts at the lowest spectral intensity between two adjacent pulsations.According to the principle of interference, we speculate that the difference in phase between soliton molecules implies a periodic transition between in phase and out of phase.
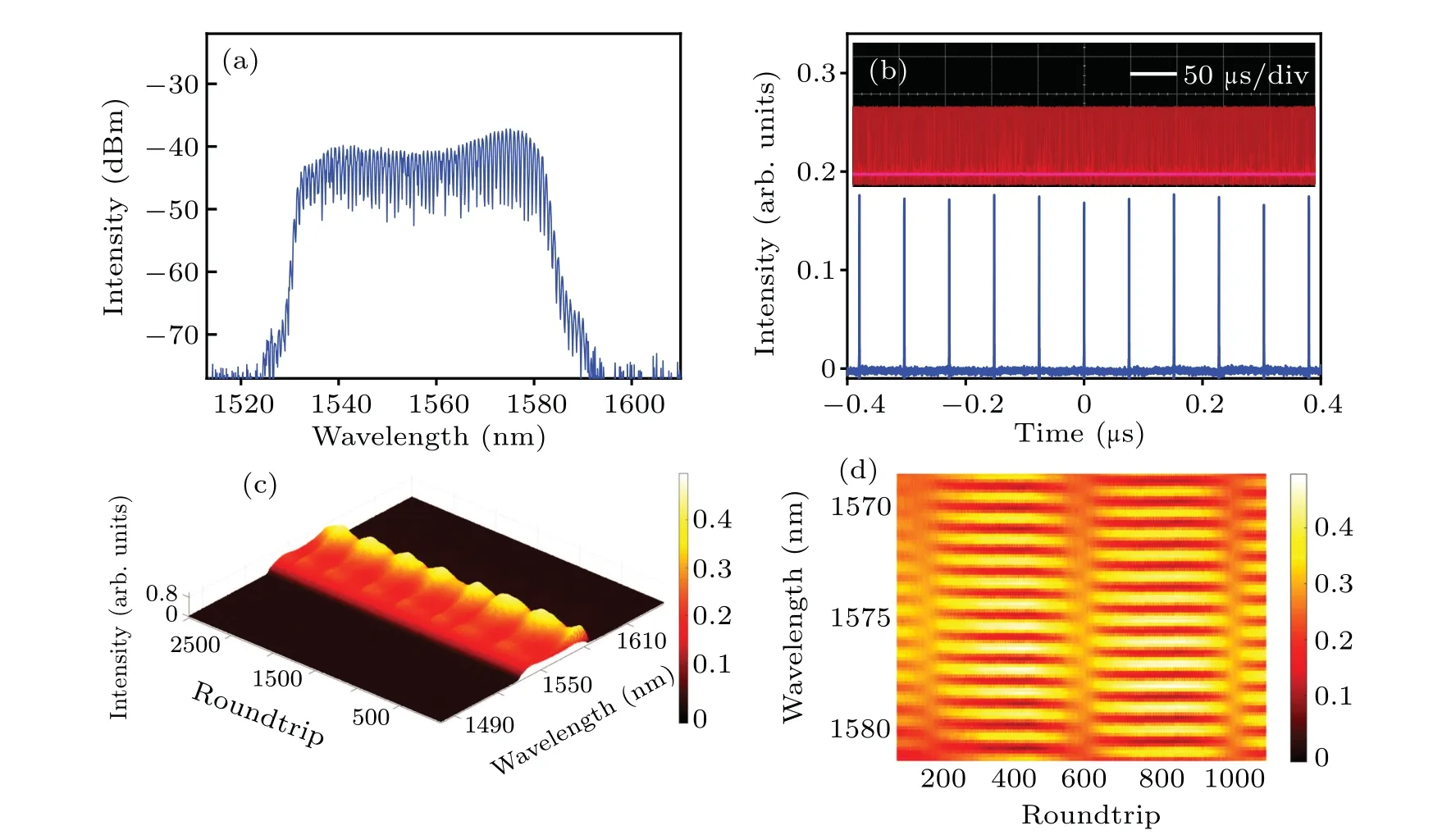
Fig.7.Invisible soliton pulsation operation.(a)OSA spectrum,(b)pulse train,(d)three-dimensional contour plot of spectra by DFT,(e)close-up of spectra.
Figures 8(a) and 8(b) present the spectral and temporal evolution during 3000 consecutive round trips, respectively.Spectral bandwidth does not vary with time, whereas the intensity does.Over cavity round trips, the pulse train remains stable.The energy evolution in Fig.8(c) is almost constant by integrating the shot-to-shot spectrum, which is consistent with stable pulse train observed by oscilloscope.The realtime spectrum varies significantly as shown in Fig.7(c).Thus,it is necessary to investigate the intermolecular pulse distribution in the time domain.To obtain the temporal information about the soliton molecule,the corresponding field autocorrelation trace is present in Fig.8(d),which is obtained by using the Fourier transform of the corresponding spectra in Fig.7(c).This method could capture transient distribution of DSs inside bound solitons.[34]Clearly, the field autocorrelation trace in Fig.8(d) confirms that the soliton molecule is composed of two solitons with unequal intensities,in which the weak soliton periodically is generated and annihilated over a period of approximately 410 round trips,indicating that the two solitons periodically exchange energy.
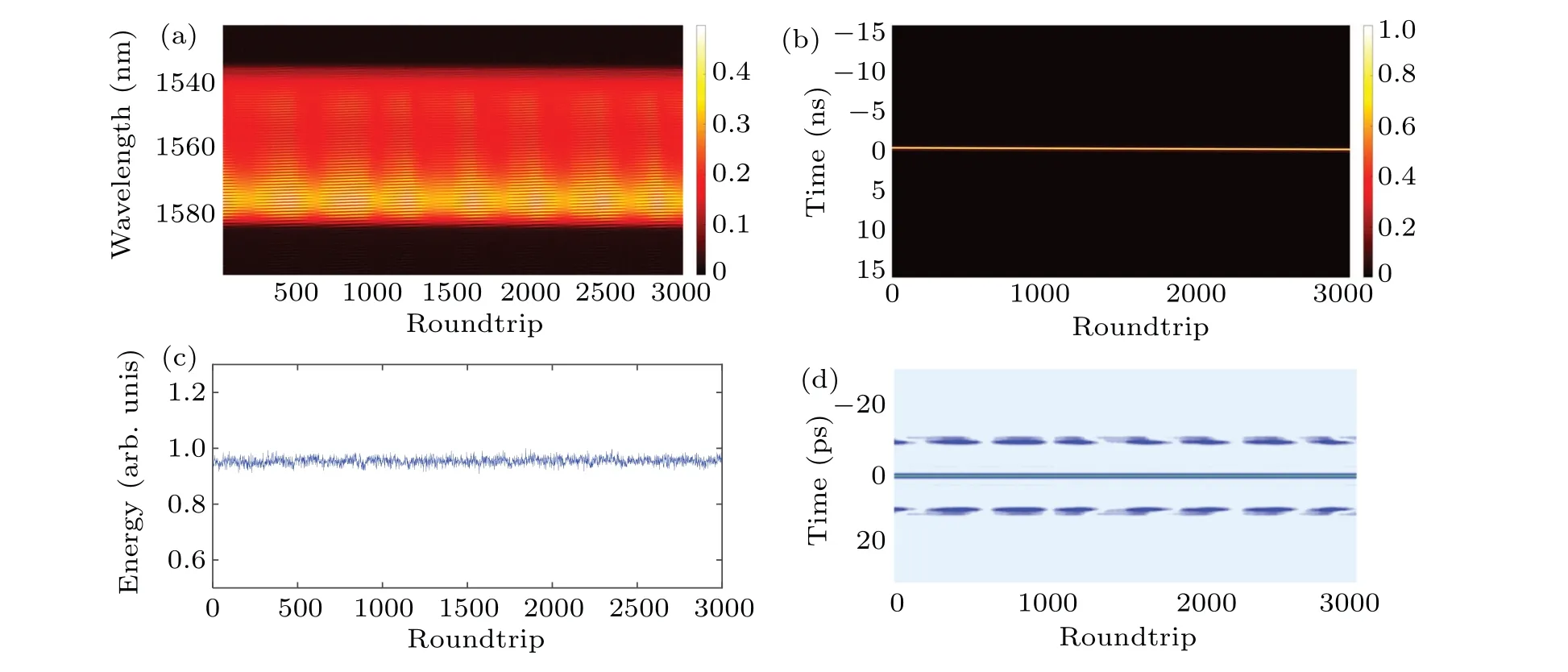
Fig.8.Evolution dynamics.(a)Shot-to-shot spectral evolution,(b)temporal evolution,(c)energy evolution,(d)field autocorrelation trace.
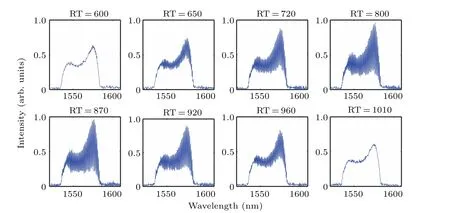
Fig.9.Transient spectral profiles within a pulsating period.
To gain an insight into spectral evolution in this case,eight typical spectral frames within one pulsating period are shown in Fig.9.The modulation depths of real-time spectra gradually increase from zero, and the normalized intensity at peak wavelength varies from 0.6 to 1 with round trips.Subsequently,the spectral modulation and intensity decrease,showing the reverse evolution trend.Combining the field autocorrelation trace in Fig.8(d),we believe that the variation in modulation depth is related to the energy oscillation of weak coherent soliton inside molecule.The larger the energy of weak soliton,the stronger the modulation depth is.The energy perturbation of weak soliton makes the spectral-modulation depth vary with round trip.In one pulsating period, the spectral bandwidth is invariable.From the real-time spectra in Fig.9,we can infer that the soliton state periodically switches between soliton molecule and soliton singlet.Despite the variation of periodic spectral profile,the spectral fringe interval remains nearly fixed at~0.73 nm over consecutive cavity round trips, implying that the soliton separation inside molecule is~11.1 ps.Such a separation matches well with the separation revealed by the field autocorrelation trace in Fig.8(d).Therefore,in the experiment,the soliton pulsates in a distinct manner; that is, real-time spectra pulsate with time but the pulse energy remains almost unchanged, which resembles the typical behavior of invisible soliton pulsation.
In this study,various soliton pulsation dynamic behaviors are investigated by using the DFT.The DFT allows us to reveal the transient dynamics of soliton pulsation through the time-stretch method.In the experiment, we find that the formation mechanism of visible and invisible soliton pulsation is different.Generally, traditional soliton pulsation(i.e., visible soliton pulsation) is related to the period bifurcation, which results from the cavity nonlinear switching effect.[35]Solitons in the dissipative system at the bifurcation point have pulsating behaviors.The pulsating soliton can periodically change its energy and spectral bandwidth.Moreover,the transformations from single- to dual-soliton pulsation can be achieved by adjusting the power pump and the PCs,indicating that the soliton pulsations are sensitive to cavity parameters such as the nonlinear effect and polarization state.As for invisible soliton pulsation,it originates from the periodic oscillation of weak soliton within soliton molecules.Owing to the energy exchange, the weak soliton periodically generates and annihilates.Therefore,the pulsation soliton periodically switches between soliton molecule and soliton singlet.In this case,although there is no change in the total energy, it could still be termed soliton pulsation because of the periodic recurrence of its profile and spectral peak intensity after multiple cycles.
4.Conclusion and perspectives
We have experimentally investigated two types of soliton pulsations in a normal-dispersion fiber laser by using the DFT technique.Traditional single- and dual-soliton pulsations, as well as invisible soliton pulsation are observed.Visible soliton pulsation exhibits obvious energy oscillation and spectral bandwidth breathing,while invisible soliton pulsation pulsates in pulse profile and peak power,but the energy is almost constant.These results provide a new insight into the dynamical process of the soliton pulsation formation.
Acknowledgements
Project supported by the National Natural Science Foundation of China (Grant No.41875040), the Natural Science Foundation of Anhui Province, China(Grant No.2008085MF211), the Foundation for Young Talents in College of Anhui Province, China (Grant No.gxyqZD2019034), and the Innovation Fund for Postgraduates of Huaibei Normal University, China (Grant No.CX2022035).
- Chinese Physics B的其它文章
- Analysis of cut vertex in the control of complex networks
- Atlas of dynamic spectra of fast radio burst FRB 20201124A
- Investigating the characteristic delay time in the leader-follower behavior in children single-file movement
- Micro-mechanism study of the effect of Cd-free buffer layers ZnXO(X =Mg/Sn)on the performance of flexible Cu2ZnSn(S,Se)4 solar cell
- Thermally enhanced photoluminescence and temperature sensing properties of Sc2W3O12:Eu3+phosphors
- Heterogeneous hydration patterns of G-quadruplex DNA

