Analysis of cut vertex in the control of complex networks

Jie Zhou(周洁) Cheng Yuan(袁诚) Zu-Yu Qian(钱祖燏)Bing-Hong Wang(汪秉宏) and Sen Nie(聂森)

1School of Electrical and Automation Engineering,East China Jiaotong University,Nanchang 330013,China

2Department of Modern Physics,University of Science and Technology of China,Hefei 230026,China

Keywords: cut vertex,controllability,control energy,structural characteristic,complex networks

1.Introduction

Research on complex networks has developed rapidly for decades, and is involved in the fields of biological,[1-3]social,[4-7]traffic,[8-10]and financial systems.[11,12]A complex network consists of nodes, which represent individuals in the complex system, and links, which symbolize the interactions between individuals.The study of complex networks is first related to networks structural characteristics,[13-16]and then refers to the performance and evaluations of systems.[17-21]If a dynamic system can be driven from any initial state to any desired state within finite time and inputs,then this system is controllable,and the minimal number of nodes that are imposed on external inputs to achieve full control can be used to measure the controllability of the system.[19]The minimal number of driver nodes which guarantees the full control of arbitrary networks has also been discussed.[22]Because the final goal of studying complex networks is to control and regulate them, many works have explained the inner relationship between structural characteristics and network control.[23-29]Furthermore,for practical problems in real control,control strategies,including energy requiring,[30-34]control modes,[35]and optimal control,[36-38]have also been considered.Reference[37]demonstrated that the control energy is involved with Gramian matrix and proposed optimal algorithm for driver nodes selection.Reference[38]analyzed the relationship between network structural characteristic and energy consumption,finding the control energy could be reduced by placing the driver nodes in a way to shorten the longest control chains for directed networks.The study of both linear and nonlinear dynamical systems has advanced network control in practical applications.[39-42]

A cut vertex is a kind of node whose removal will disconnect the network and increases the number of connected components in a network.[43,44]Due to its significant role in network topological structures, its removal has a serious impact on network connectivity and robustness.[45-47]For example,in transportation systems,the failure of airports,which is cut vertexes in the corresponding network, will lead to largescale congestion in traffic.[48]Due to its vital position in network structure, the role of cut vertex in network controllability is also considered.Wanget al.[46]studied the influence of cut vertex removal on the controllability of network and found that the failure of cut vertex largely decreases controllability compared to the removal of other vertexes, and the network robustness results were similar.However, how cut vertex affects network control, especially for the control energy, has not yet been explained.According to the previous works on network control, the influence of nodal structure on network controllability and control energy is still insufficient and the role of nodes in control remains to be explored.

In this paper,we discuss the relationship between the cut vertexes and the driver nodes, and find that cut vertexes are more likely to be redundant nodes for network control.Selecting cut vertexes as driver nodes is beneficial for the control energy.In addition, the removal of cut vertexes will largely increase the control energy since cut vertexes are nodes with larger degrees.The model and method are introduced in Sections 2 and 3.Section 4 is our results and Section 5 is conclusion.

2.Model

We firstly consider a linear time-invariant dynamical system withNnodes as[49]

wherex(t)=(x1(t),x2(t),...,xN(t))Tdenotes the state of the nodes at timet.A=(ai j)N×Nis the adjacency matrix which represents the interactions between nodes, whereaijrepresents the link starting from nodeito nodej.B=(bij)N×Mis the input matrix, which describes how the external inputs affect nodes, andu(t)=(u1(t),u2(t),...,uM(t))Tis the vector of external inputs.

If the dynamical system can be driven from any initial state to any desired state within a finite time by finite external inputs, then the system is controllable.[50]According to the Popov-Belevitch-Hautus(PBH)rank condition in control theory,[51]the system(1)is controllable if and only if

which is satisfied for any complex numberc,whereINis the identity matrix of dimensionN.To find the setBto guarantee that Eq.(2) is satisfied, the minimal number of driver nodesNDshould equal the value of min{rankB},and it can be calculated as[22]

whereλi(i=1,2,...,N)is the distinct eigenvalues of matrixA, andµ(λi) =N-rank(λiIN-A) is the geometric multiplicity of the eigenvalueλiofA.In practical terms,NDcan be considered as a metric to evaluate the controllability of networks.[19,22]

3.Method

3.1.Cut vertex

The depth-first search is used to identify all the cut vertexesVi(i=1,2,...,m)in a network.[52]The steps are as follows.(1) Calculate the number of connected subgraphsCoin the original network, then remove nodeiand calculate the number of connected subgraphsCiof the current network.(2)CompareCiwithCo.IfCi＆gt;Co,the number of connected subgraphs has increased, then nodeiis the cut vertex and marks it asVi.(3)Restore the original network,then repeat the steps from step(1)for the next node.After all nodes are traversed,the cut vertex setVi(i=1,2,...,m)is collected,andmis the total number of the cut vertexes.

3.2.Driver nodes

Identifying driver nodes According to the framework of exact controllability,[22]the minimal number of the driver nodesNDcan be obtained by the maximum geometric multiplicityµ(λi) of the adjacency matrixA.The control matrixB, which describes how nodes affect external inputs, should satisfy the equation rank[λMIN-A,B]=N,whereλMcorresponds to the maximum geometric multiplicityµ(λM).Thus,identifying the minimum set of driver nodes can be equivalent to setting rows ofBto ensure that the matrix[λMIN-A,B]is full rank.By implementing an elementary column transformation on the matrixλMIN-A, a set of linearly dependent rows is obtained.Then,inputs are imposed via control matrixBon the identified rows to eliminate the linear correlations and guarantee that the matrix [λMIN-A,B] is full rank.In matrixB, the nodes corresponding to the linearly dependent rows are the driver nodes.[22]For the same network,there are different combinations of the driver nodes,however,the minimal number of the driver nodes is identified.

Node categories According to the different control roles,nodes can be classified into three categories.[22,23]Critical:the nodes are always selected as driver nodes.Their removal will lead to the increment ofND.Redundant: the nodes can never appear in the minimal driver node set.If a redundant node is selected as a driver node,thenNDwill be increased.Intermittent: the nodes which are not critical or redundant.They can be chosen as driver nodes in some control configurations.

4.Result

Since cut vertexes play an important role in the topological structure of network,the minimal number of driver nodes is also determined by the network’s structural characteristics.We first explore the distribution of the different categories of nodes in cut vertexes to determine whether there is any relationship between the driver nodes and the cut vertexes.The cut vertexes are identified by the deep-first search (see Subsection 3.1).For both undirected Erd¨os-R´enyi (ER) random graphs[53]and scale-free(SF)networks,[54]the distribution of the node categories is shown in Figs.1(a)and 1(b).Comparing the distributions of the critical,intermittent,and redundant nodes in the network, we find that most nodes are redundant.The cut vertex set consists of only intermittent and redundant nodes, in which the predominant node category is the redundant one.Although cut vertexes are essential for network connectivity,the driver nodes are more likely to avoid them.Similar results are found for directed Erd¨os-R´enyi(DER)random graphs and directed scale-free (DSF) networks in Figs.1(c)and 1(d).

Furthermore,we examine the role of cut vertexes in network control.We employ three strategies to identify theqdriver nodes in the network withmcut vertexes.Strategy 1:qdriver nodes are chosen randomly.Strategy 2: Ifq ≥m(mis the number of cut vertexes),mdriver nodes are chosen based on the descending order of the nodes’degree,and the remaining nodesq-mare chosen randomly.Ifq＆lt;m,qdriver nodes are chosen based on the descending order of the nodes’ degree.Strategy 3:Ifq ≥m,all cut vertexes are chosen as driver nodes,and the remaining vertexesq-mare chosen randomly.Ifq＆lt;m,qdriver nodes are chosen randomly from the cut vertexes set.

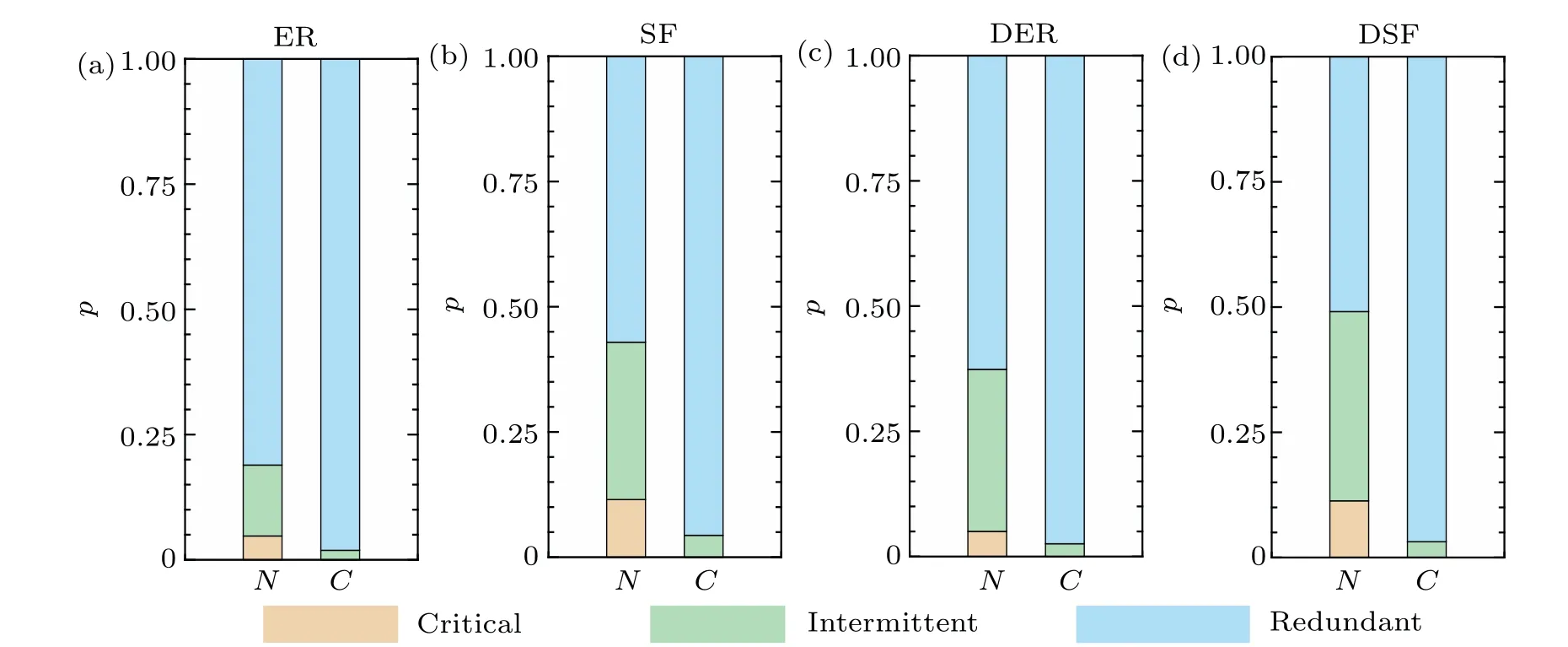
Fig.1.Node category distribution.(a)Undirected random graph,(b)undirected scale-free network,(c)directed random graph,and(d)directed scale-free network.The network size is N=300,average degree is K=3,and degree exponent for the undirected scale-free network is γ=2.5 and for the directed scale-free network is γin=γout=2.5. N represents all nodes in the network,and C represents the cut vertex set.We obtain the node categories for 100 networks and obtain the average value of the distribution.

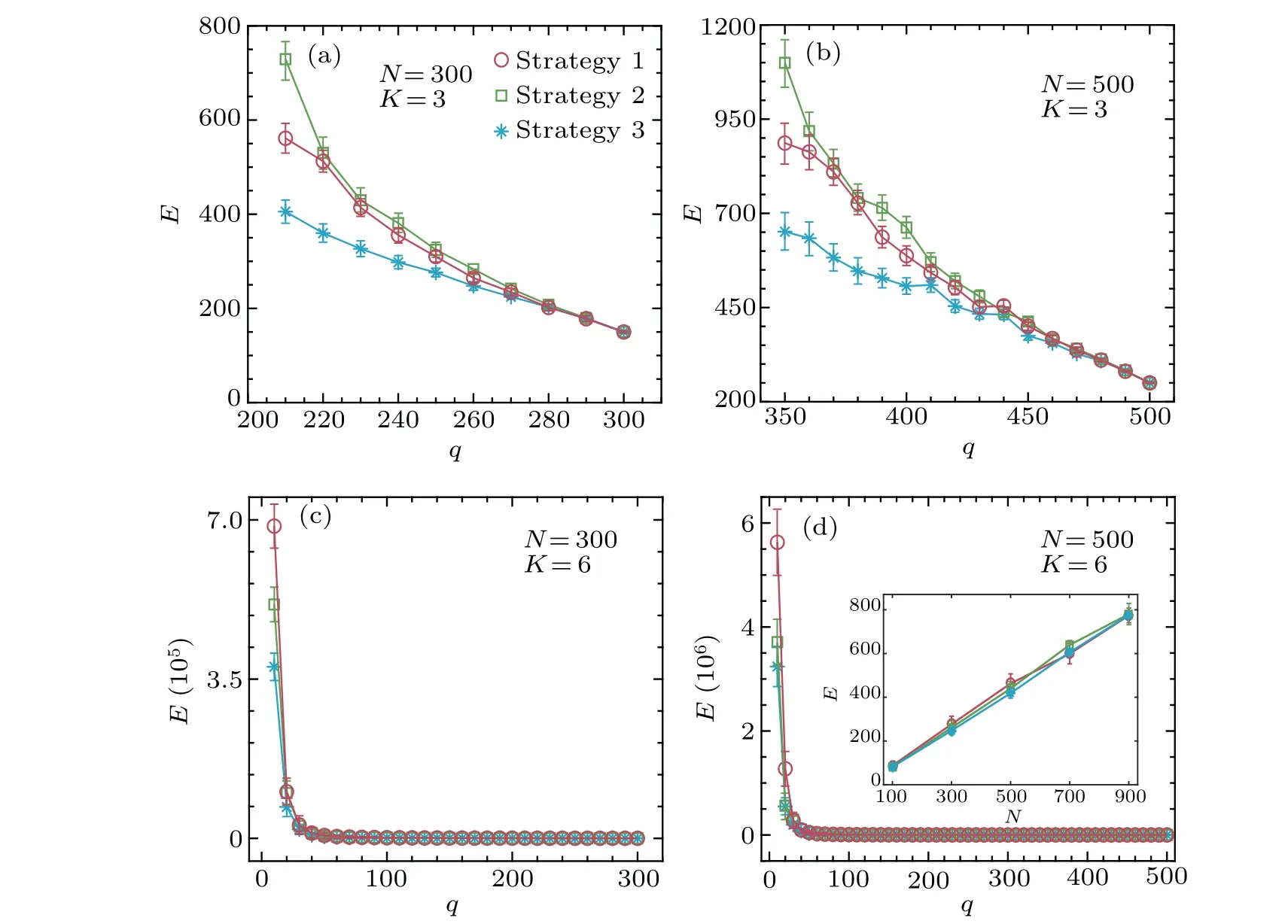
Fig.2.Control energy as a function of the number of driver nodes q with different control strategies for undirected random networks.(a)The network size is N=300,and the average degree is K=3.(b)The network size is N=500,and the average degree is K=3.(c)The network size is N=300,and the average degree is K=6.(d)The network size is N=500,and the average degree is K=6.The insert figure shows the control energy among random networks with three strategies for different network size.The average degree is K=3 and q is 85%of network size.For(a)and(b),the starting point of q is 70%of network size.The error bars represent standard deviations and each data point is the mean of 100 independent realizations.

The results show that cut vertexes are significant for the control energy in random networks (see Fig.2).Driving cut vertexes will reduce the energy required compared to driving randomly chosen nodes or hub nodes.As the number of driver nodes increases, the differences of control energy obtained by the varied strategies decrease.This is because the proportion of the cut vertexes in the driver nodes decreases asqincreases.Furthermore,the difference in energy requirements among networks with the three control strategies is similar for different network size.The insert figure shows the control energy is the lowest one as cut vertexes are selected as the driver nodes with increasing network size.Meanwhile, because the number of cut vertexes is affected by network density,the energy gaps among the three strategies are smaller with denser networks.

Similar results are found for scale-free networks and are shown in Fig.3.The control energy is the lowest when driving cut vertexes is preferred with a small amount of driver nodesq(q＆lt;230 for Fig.3(a),q＆lt;150 for Fig.3(b)).As the number of driver nodes increases,the energy gap among the three control strategies is almost gone.In addition,the advantage of cut vertexes in reducing the control energy is weakened in more homogeneous network.Due to their structural characteristic,cut vertexes are the connections of the connected subgraphs of networks and are more likely to be the intermediate nodes in control chains.For directed networks,a chain starts from a driver node and ends at a non-driver node, along the shortest path between these two nodes is the control chain.[38]Control energy flows through the control chains, and the longest control chains (LCCs) determine the control energy.Thus,shorter LCCs lead to the lower control energy.For undirected networks, choosing cut vertexes as driver nodes result in the shorter control chains as well.A control chain starting from a cut vertex to a non-driver node will be shorter than that of a chain that starts at a node in one connected subgraph and goes to a non-driver node in another connected subgraph.Thus,the control energy is markedly reduced.

Fig.3.Control energy as a function of the number of driver nodes q with different control strategies for undirected scale-free networks.(a)The network size is N=300,and the degree exponent is γ =2.5.(b)The network size is N =300, and the degree exponent is γ =3.The average degree for both networks are K =6.The error bars represent standard deviations and each data point is the mean of 100 independent realizations.

According to the previous findings,[46]the failure of cut vertex affects the robustness and controllability of network.Here, we explore the effect of cut vertex failure on network control energy.To disable cut vertexes(CV-preferred),we execute the following steps.(1) Identify all cut vertexes in the current network by the depth-first search(see Subsection 3.1)and mark them asVi.(2) Calculate the number of connected subgraphsC＇iin the current network if each cut vertexViis removed.(3) Disable a fraction of the cut vertexes based on the descending order of theC＇ivalue,remove all the edges connected with them,and then calculate the control energy needed to steer all nodes from the initial state to the final state.(4)Repeat the steps from step(1)until there are no more cut vertexes in the current network.

In addition, we employ another two node-failure strategies[55,56]to compare the effect of nodal failures on control energy.(1)Random: disable nodes randomly and remove all the edges connected with them.(2)Degree-preferred: disable nodes based on the descending order of the nodes’degree and remove the corresponding edges.The other steps for repeatedly calculating the control energy and disabling nodes in the current network are all similar to those of the CV-preferred strategy.Furthermore, the number of disabled nodes at each step must be the same for all three strategies, and then the comparison of the control energy can be valid.

The results in Fig.4 show that the sparse random network requires more energy to drive the whole network with the degree-preferred failure strategy.However, it is easiest to control the network with the random failure strategy.For dense network, with a proper fraction of disabled nodes, the control energy for the driving network is the lowest with the CV-preferred failure strategy (see Fig.4(b)).Similar results can be found for scale-free networks, and they are shown in Figs.4(c)and 4(d).The network costs less energy to achieve full control with the Random failure strategy,while the energy requirements are higher for networks with CV-preferred and degree-preferred failure strategies.For more homogeneous network(see Fig.4(d)),the difference in control energy among the networks with the three failure strategies is smaller.

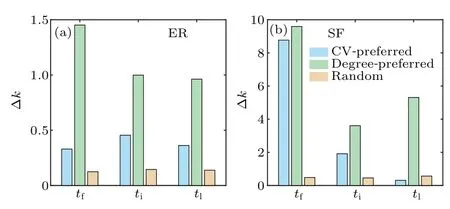
To explain the result of the CV-preferred strategy in Fig.4,the average degree of the failed nodes in the failure process is investigated.We define Δk=(kf-ka)/kato describe the degree difference between the failed nodes and the other nodes in network.kfis the average degree of failed nodes at each step of node-failure process andkais the average degree of all nodes at each step of node-failure process.For each strategy, we calculate Δkat the first step of failuret=tf, the intermediate stept=ti,and the last stept=tl.Figure 5 shows the results of random network and scale-free network, and it illustrates that cut vertexes are nodes with larger degrees in the network.The gap of Δkbetween the random strategy and the CV-preferred strategy is small,leading to a small difference in control energy,which is shown in Fig.4(b).For the scale-free network, Δkof the random strategy is always small.While for the CV-preferred and the degree-preferred strategies,Δkis large at the first step then decreases markedly in the following steps.Thus, the gap of Δkbetween the random strategy and the others two strategies is large,resulting in the large energy gap as shown in Fig.4(c).

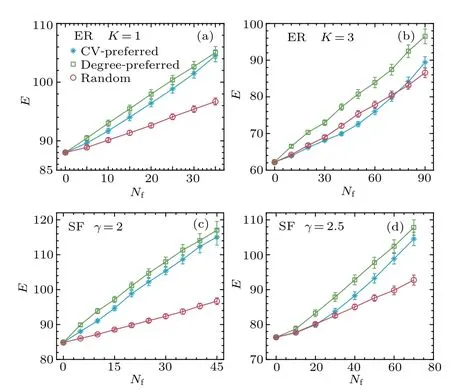
Fig.4.Control energy as a function of the number of disabled nodes Nf with three failure strategies for directed networks.(a)The network size is N =300, average degree is K =1.(b) N =300 and K =3.(c) N =300, K =3, and the degree exponent is γin =γout =2.(d)N=300,K=3,and the degree exponent is γin=γout=2.5.The error bars represent standard deviations and each data point is the mean of 100 independent realizations.

Finally, we test our results on real networks.[57,58]Figure 6 shows the control energy for driving real networks with the different control strategies.The results are similar to those of the synthetic networks, where driving cut vertexes favors control energy.With an increasing number of inputs, the difference in the energy required with the three control strategies disappears.

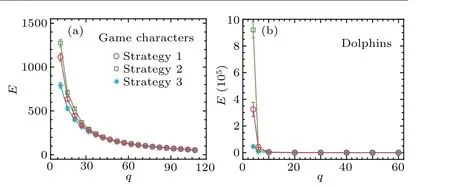
Fig.6.Control energy as a function of the number of driver nodes q with different control strategies for real networks.(a)Game characters.A network of coappearances of the characters in the Game of Thrones series.[57] The network size is N=107,and the number of edges is L=353.(b)Dolphins.An undirected social network of frequent associations is observed among 62 dolphins.[58] The network size is N =62, and the number of edges is L=159.The error bars represent standard deviations and each data point is the mean of 100 independent realizations.

5.Conclusion

Considering that cut vertexes play a vital role in the network structure, we discover the correlation between cut vertexes and driver nodes and explore the influence of cut vertexes on the network control energy.Our results show that the minimal driver node set,based on exact controllability framework, tends to avoid cut vertexes.However, compared with random nodes and hub nodes,driving cut vertexes can reduce control energy.Imposing inputs on cut vertexes will shorten the control chains, which determine the control energy.Furthermore, being the larger-degree nodes in network, the cut vertexes’failure affects the control energy more than the failure of random nodes.Finally, the results are verified on real networks.Though our results indicate the role of cut vertexes play in controlling, some specific control constraints need to be taken into account in the future, such as the control time and control trajectory.Moreover, nodal dynamics is simplified in our model and how does it impact the controllability and control energy is still a crucial issue for controlling which remains to be solved.In conclusion,this work bridges the gap between structural characteristics and network control, and it will be helpful for understanding the nodal importance in optimal control.

Acknowledgements

Project supported by the National Natural Science Foundation of China (Grant No.61763013), the Natural Science Foundation of Jiangxi Province of China (Grant No.20202BABL212008),the Jiangxi Provincial Postdoctoral Preferred Project of China (Grant No.2017KY37), and the Key Research and Development Project of Jiangxi Province of China(Grant No.20202BBEL53018).