考虑结构耦合弧形闸门动力特性分析

王晋美，张慧桢，晋翔宇，李沙沙

（黄河交通学院机电工程学院 河南 焦作 454150）

0 引言

闸门是水工金属结构中不可或缺的一部分，闸门安全稳定的运行是水利枢纽设施建设的一个重要基础。大量研究表明，振动引起的闸门失效是闸门失效破坏的主要原因之一[1]。

近年来，闸门的振动问题得到了广泛的研究。马斌等[2]通过对乌东德水电站进行水弹性模型实验，分析了表孔闸门不同开度工况下水电站拱坝的动力响应特性，得出闸门的开度会影响水垫塘底部以及边坡的振动响应。谢涛等[3]对角木塘水库露顶式弧形闸门进行了模态分析，发现由水体的耦合会使闸门前20阶固有频率降低35%～62%，且水体附加质量对闸门低阶固有频率影响较大。李桑军等[4]通过仿真分析研究了弧形闸门不同水头以及不同开度下的固有频率，结果表明闸门开度会改变闸门与水体的耦合部位面积，从而改变闸门的固有频率。杨佼佼等[5]基于混沌理论对弧形闸门面板的振动特性进行了研究，表明闸门面板在高水位时振动复杂程度高，小开度时闸门面板振动的线性相关性高。Ren等[6]对某叠梁闸门进行了仿真分析和模型实验研究不同工作条件下水体的激振特性，研究表明流道通风口形状、上游水位等因素都会影响水流激振特性。Lian等[7]对锦屏水库中孔闸门启闭引起表孔闸门振动的这一现象进行研究，得出了接近弧形闸门固有频率的相邻的闸门和坝体产生的激励会对弧形闸门的振动产生影响，其研究也表明拱坝会通过与闸门的接触部位对闸门产生振动激励。

综上所述，闸门的动力响应特性除了受闸门自身的结构性能影响以外，闸门与其相邻结构的耦合、水体的附加质量等都会影响闸门的动力响应，因此，在考虑闸门动力特性时不但应从闸门结构本身出发，同时也需要考虑闸门与其他结构的耦合对闸门动力特性的影响。基于此，本文以某水库溢洪道中间闸室和闸门的耦合系统为研究对象，对闸门、闸门—闸室耦合系统以及考虑水体附加质量的闸门—闸室耦合系统进行模态分析，并进一步考虑不同耦合情况对闸门的固有频率和动力响应的影响。

1 理论计算

仅考虑弧形闸门的振动特性，可以将闸门简化为弹簧—阻尼单自由度系统，如图1所示。闸门的振动微分方程可表示为：

图1 闸门单自由度简化模型

式中m为闸门的质量，c和k分别对应闸门系统的阻尼和刚度，P（t）为闸门受周期载荷情况，认为闸门受到简谐载荷，即：

式中，P0为简谐载荷幅值。系统稳态响应可表示为：

式中，Y为稳态响应幅值，结合式（1）～（3），系统响应幅值为：

利用模态分解技术，可以将复杂多自由度系统的振动问题转化为二自由度系统的振动问题，从而使计算更加方便，复杂多自由度闸室—闸门系统的简化表示如图2所示。

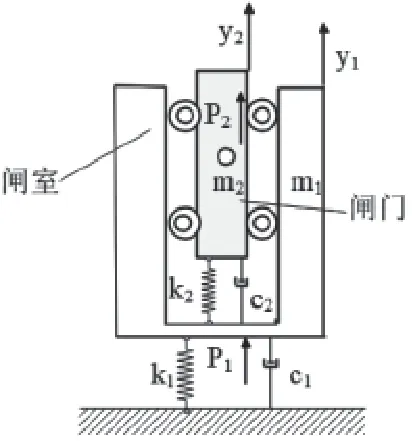
图2 闸门—闸室耦合系统二自由度简化模型

二自由度有阻尼系统振动系统可以表示为：

式中，m1、c1和k1分别代表闸室的质量、阻尼以及刚度，m2、c2和k2分别代表闸门的质量、阻尼以及刚度，ÿ1、y·1和y1分别代表闸室结构的绝对加速度、速度以及位移，ÿ2、y·2和y2分别代表闸门结构的绝对加速度、速度以及位移。P1（t）和P2（t）分别表示闸门和闸室结构受外部激励载荷。将闸门和耦合系统受到的载荷视为频率相近的简谐波动载荷，即

式中P′i为简谐部分幅值，i取1和2，ω为简谐波动频率。相应的，系统的稳态响应可表示为：

Yi为系统响应幅值，根据式（5）～（9），系统响应幅值可表示为：

闸门是相对闸室运动的结构，闸门的运动会使闸门—闸室耦合的结构形式发生改变：当闸门关闭时，闸门、闸室之间既有铰链的连接也有闸门底部与闸室的直接接触，而闸门开启时，闸门和闸室仅通过支铰结构连接。因此，闸门对应的启闭状态也会影响闸门—闸室耦合结构的动力响应。结合闸门—闸室二自由度响应模型进行分析：闸门在承受水流简谐波动载荷时，闸室前面也会承受与闸门同频率的简谐载荷；闸门关闭时，闸室通过地面与支铰连接处将载荷传递给闸门；闸门开启时，闸室通过支铰处将载荷传递给闸门。相应的，式（5）中P2（t）可进一步表示为：

P2d（t）和P2z（t）分别代表闸室通过底边和支铰传递给闸门的载荷，闸门动力响应可表示为：

动力响应幅值为：

当闸门开启时P2d为0，因此闸门关闭时频率响应幅值应大于其开启时频率响应幅值，即在闸门开启后，闸门动力响应的位移幅值会变小。

图3 闸室对闸门的载荷传递

水流的附加质量同样会影响闸门的动力特性，以闸门—闸室耦合系统整体为研究对象，考虑水体附加质量时，闸门系统可简化为图4。

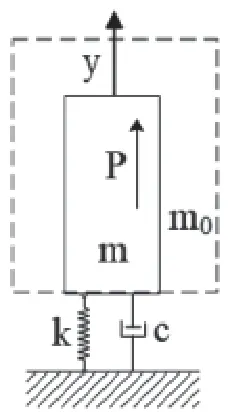
图4 考虑附加质量的闸门简化模型

在考虑水体附加质量时，系统固有频率为：

式中ω0为考虑水体时系统的固有频率，m0为水体的附加质量，ξ为系统阻尼比。显然水体附加质量会使系统固有频率降低。

2 数值分析

2.1 有限元模型

以某水库溢洪道中间闸室和闸门耦合系统为研究对象，根据结构的几何特征建立闸门—闸室结构耦合系统有限元模型。弧形闸门跨度为12 m，高度为10.5 m，闸门的弧面半径为14 m，支铰相对弧形闸门底槛高度为11m，闸室两侧闸墩厚度为3.75 m，闸墩高度为19 m，闸室底部厚度为1.8 m。闸门面板、支臂、横梁、纵梁等结构采用壳单元建立有限元模型，闸门支铰和闸室采用实体单元建模，建立的有限元模型如图5所示。闸门支铰与闸室通过铰链连接，闸门两侧与闸室壁面有摩擦接触，摩擦系数为0.2，闸门关闭时，闸室底部对闸门有位移支撑约束。闸门和溢洪道铰链材料为Q345 B，密度为7 850 kg/m3，杨氏模量为201 GPa，泊松比为0.3；闸室为混凝土结构，其密度为2 360 kg/m3，杨氏模量为22 GPa，泊松比为0.2。考虑水体附加质量时，在闸门前建立6.5 m深的水体。

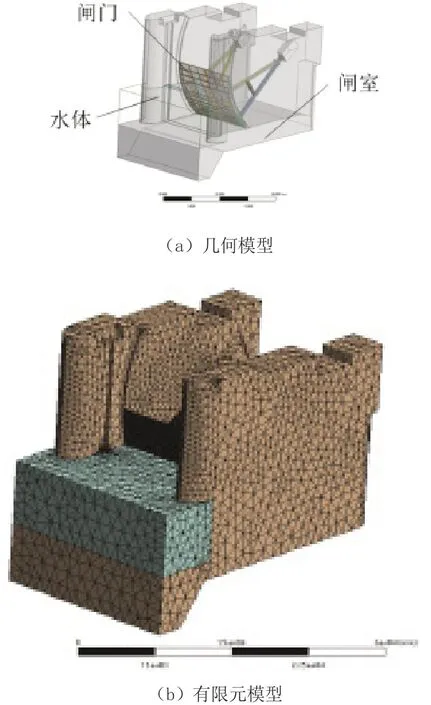
图5 闸门模型

2.2 动力学分析

对闸门进行动力学分析，结合本文第1节描述，闸门开启状态和闸门关闭状态对应的闸门—闸室系统耦合形式不同，且水体附加质量会对闸门的动力响应产生影响，因此分析以下四种不同情况闸门的固有频率：

（1）情况1：不考虑系统耦合，分析闸门固有频率；

（2）情况2：分析闸门—闸室耦合系统在闸门关闭时的固有频率；

（3）情况3：分析闸门—闸室耦合系统在闸门开启时的固有频率；

（4）情况4：分析闸门—闸室耦合系统在闸门关闭时考虑水体附加质量下的固有频率。

不同情况下，闸门及耦合系统的各阶模态反应如图6所示。闸门各阶振型对应的主要振动部位为闸门支臂、闸门面板和闸门纵梁翼板，振动形式表现为：支臂绕支铰圆心转动和支臂上下摆动、门面板上部分出现扭转振动以及闸门面板局部发生颤动、纵梁翼板向内或向外扭转振动。闸室的振动部位为闸室两侧闸墩，振动形式为闸墩绕闸墩根部摇摆或扭曲振动。

图6 闸门各阶模态

模态分析云图6显示，闸门—闸室耦合系统模态分析结果中第2、3、4、5、8、9、13、14、17、18阶振型为闸室振动，说明各阶模态结果中有部分结果仅反映闸室的振动特性。仅考虑不同情况下闸门的各阶固有频率，忽略闸门—闸室耦合系统中第2、3、4、5、8、9、13、14、17、18阶固有频率，将剩下的各阶固有频率重新排列，对应的4种情况下闸门的固有频率如图7所示：

图7 闸门固有频率

对比第1、2、3组数据，闸室与闸门耦合会增大闸门的各阶固有频率，闸门—闸室结构耦合系统对闸门本身固有频率影响极小。对比第2、3组数据，考虑结构的耦合，闸门关闭时固有频率略小于其开启时固有频率。对比第2、4组数据，在水体耦合作用下，闸门的各阶固有频率都会降低40%左右。

2.3 谐响应分析

对闸门进行谐响应分析，分析闸门—闸室耦合作用对闸门频率响应特性的影响。在计算中，分析闸门在（0～60）Hz频率范围内的响应情况。针对闸门进行谐响应分析，在闸门面板按水压力分布规律给每个节点施加简谐载荷幅值，相位角为0；在对闸门—闸室耦合系统进行谐响应分析时，分别取闸门关闭和开启1 m两种不同工况，在闸门面板和闸室迎水侧同时施加简谐载荷幅值，相位角为0。闸门的频率位移曲线如图8（a），闸门关闭时闸门—闸室耦合结构中闸门的频率位移曲线如图8（b），闸门开启时闸门—闸室耦合结构中闸门的频率位移曲线如图8（c）。

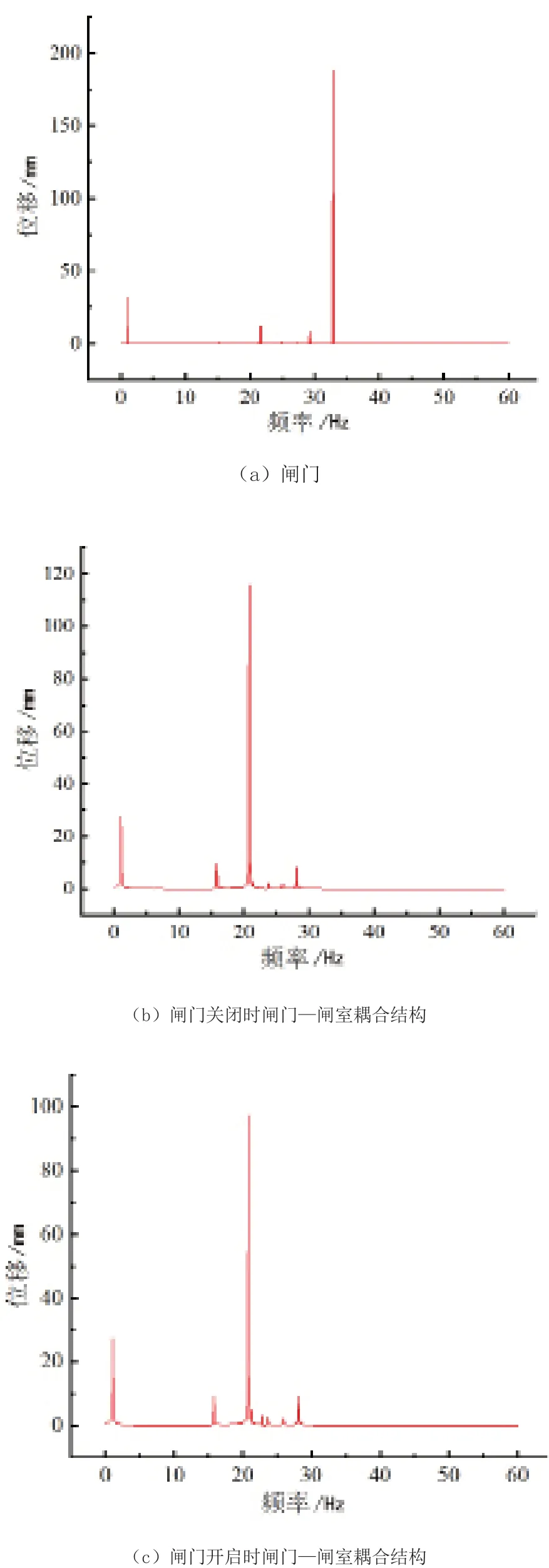
图8 不同情况下闸门幅频特性曲线

对比图8中（a）、（b）、（c），考虑闸门—闸室结构耦合后，闸门最大位移响应的频率和最大位移值均减小，对应最大位移的频率由32.9 Hz减小为20.8 Hz，最大位移由189.7 mm分别减小至115.95 mm和97.24 mm。这是由于考虑结构耦合后，系统的刚度变大，刚度增大导致最大响应的幅值和对应的频率均减小，与式（4）的理论推导结果一致。图8中（b）、（c）分别表示闸门关闭和闸门开启状态对应的频率位移曲线，两种情况下闸门达到最大位移对应的频率均在21 Hz附加，然而最大位移分别为115.95 mm和97.24 mm。闸门关闭状态下，闸室可通过支铰和闸门底部向闸门传递载荷，而闸门开启时，闸室仅通过支铰向闸门传递载荷，导致闸门开启状态下最大位移小于闸门关闭状态最大位移，与式（12）的推导结果一致。

闸室的频率位移曲线如图7所示，闸室出现位移峰值的区间为（20～26）Hz，因此闸室的振动有一定概率引发闸门产生共振，闸门在运行过程中存在一定安全隐患。可适当增加闸室两侧闸墩的厚度，从而使闸室结构的刚度增大，增大闸室最大位移对应的频率。将闸墩厚度增加500 mm，对应图9中闸门位移峰值对应的最大频率为23 Hz左右，改进后闸门不会和闸室产生共振。

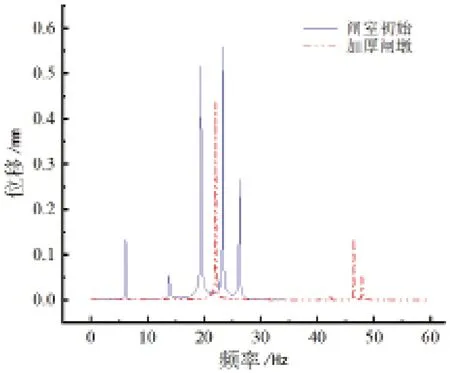
图9 闸室幅频特性曲线

3 结论

本文以某水库溢洪道中间闸室为研究对象，通过构建闸门单自由度简化模型和闸门—闸室系统的二自由度模型进行闸门动力响应特性的理论分析，并利用数值分析的方法建立闸门—闸室耦合模型有限元模型对闸门的动力响应特性进行理论分析，得出以下结论：

（1）考虑闸门和闸室的耦合，耦合结构会使闸门的计算刚度增大，导致弧形闸门的闸门固有频率增大（0.5～1）Hz。

（2）理论分析和幅值结果都表明，考虑水体与闸门耦合后产生的附加质量闸门的固有频率会降低。

（3）闸门动力学模型表明，结构耦合会影响闸门的动力响应的幅频特性，谐响应分析进一步表明，考虑结构耦合后闸门最大位移对应的激励频率会明显降低。因此在考虑闸门动力响应问题时，必须考虑结构耦合带来的影响。

（4）闸门与闸室结构耦合的形式对闸门谐响应分析中最大位移对应的激励频率没有影响，闸门开启和关闭对应的不同载荷形式通过改变激励的传递方式来改变闸门谐响应分析中的最大位移。