光学干涉教学中噪声因素的探究——以散射光聚焦为例

洪佩龙，易明芳

（安庆师范大学 数理学院，安徽 安庆 246133）

光学在现代信息技术、先进制造和精密测量等领域发挥着重要作用，已成为推动科技进步和社会发展的关键驱动力[1-2]。随着光学技术的不断发展，世界主要创新型国家对光学技术人才的需求日益迫切，产业界亦面临着光学技术人才短缺的困境[3]。近年来，我国施行“新工科”教育改革，对培养光学领域创新型人才提出了更高要求[4-6]。在这一背景下，光学人才的培养既要深化理论功底，又要紧扣工程创新能力[7-8]。然而，传统光学课堂往往偏重基础理论的传授，而缺乏对理论知识与工程应用联系的讨论[9-10]。因此，在光学教学中，引入既具有理论深度又能与工程实际相结合的案例成为新的挑战。

光场干涉是光学课程的核心概念[11]。光场干涉教学一般从最基础的两路径叠加出发，讲清楚杨氏双缝干涉、迈克尔逊干涉仪、牛顿环等；然后深入到多路径叠加，讲解多缝光栅、法布里珀罗干涉仪、薄膜干涉等。无论是在两路径叠加还是在多路径叠加中，光学路径间的相对相位是决定和分析干涉增强或减弱的关键。这一关键点也体现在光子学前沿研究中，为了将散射光场汇聚到某一特定的观测点，必须使得多条散射路径间的相位差为2π的整数倍。目前，先进的波前整形技术正是基于该原理，先通过实验测定散射路径间的相位差，然后利用光场调控设备来补偿该相位差，进而实现散射光的聚焦。

此外，光场干涉也是众多先进光子学技术所涉及的基本原理，包括光谱探测、表面形貌精密测量、光学成像等。然而，在实际光学装置中，噪声会不可避免地影响实验的测量结果，并在很大程度上决定着光学装置的灵敏度乃至可行性[12]。尽管传统课堂对光场干涉基本原理的讲解较为详实，但对干涉特性与噪声内在联系的讨论尚有欠缺。为此，本文将光学前沿研究中的散射光聚焦引入到课程教学中，并基于仿真实验系统地探讨噪声对聚焦效果的影响，以期阐明噪声对光学干涉装置的重要作用。该案例结合光学前沿来探究光学干涉中的噪声因素，一方面引导学生将理论知识与实际应用相结合，从而培养学生的工程思维；另一方面促使学生将课本知识和前沿研究联系起来，从而形成对光子学技术中非理想因素进行系统性思考的习惯，并最终促进高水平光学人才的培养。

1 散射光场聚焦的基本理论

无序介质是指结构具有一定无序度的材料，在自然界中广泛存在，如生物组织、云层、墙面等。光在无序介质中传播时，会经历多重散射过程，最终在出射端呈现出散斑现象；实现散射光场聚焦是复杂光场调控领域的前沿热点问题[13]。目前，波前整形技术是实现散射光场聚焦的核心技术，其基本原理为光学课程中重点讲述的多路径干涉增强。本文首先阐述了波前整形的工作原理，随后讨论了实际装置中噪声对散射光聚焦效果的影响。

光场的多重散射是一个线性光学过程，可以用散射矩阵来描述。假设将入射光场和透射端散射光的每一个空间模式按顺序排列，分别构成列矢Ein和Eout。如果入射端可调的空间模式数目为N，则Ein为一个包含N个元素的列矢。同理，列矢Eout大小取决于出射端光场的空间模式数目。那么，可以引入一个二维透射矩阵T来描述无序介质对光场的散射，而且透射端和入射端散射光场存在如下数学关系[14]：

其中，针对无序散射介质，透射矩阵T的每一个矩阵元是随机且满足高斯分布的复数[14]。

从公式（1）可知，Eout的一个元素表示某一出射位置的散射光场，由Ein中的不同入射模式经过T所表示的不同散射路径叠加形成。由于这些散射路径之间的相位随机分布，散射光场表现为明暗不同且无序的散斑，其光强满足瑞利分布。为了实现散射光的聚焦，一般通过控制入射光的复振幅分布来实现：

其中，Etar代表在目标位置产生聚焦点的目标列矢量，T+是T的转置共轭矩阵。这时，将Efoc代入公式（1）的入射列矢Ein，则不同散射路径之间的相位保持一致，并产生多路径干涉增强。

因为T通常不是完备的散射矩阵，所以散射光的聚焦并不完美。经过波前整形，散射光场除了会在目标位置产生一个干涉增强的聚焦点，其它位置依然会存在如图1所示的剩余散斑。此外，在波前整形装置中，光场调控设备如空间光调制器往往只控制入射光的波前相位，而不是复振幅，因而在入射光波前引入了额外的误差，从而导致剩余散斑进一步增强。为了表征散射光的聚焦效果，一般采用聚焦位置光强的增强倍数来定量描述，即聚焦增强系数η：

图1 基于波前整形实现的散射光聚焦

其中，Ifoc是经波前整形后目标位置聚焦点的光强大小，Ibg是目标位置散斑光强的系综平均值。为了得到系综平均后的透射光场，可在入射光加载若干个随机波前，对获得的透射光强求平均。根据平均透射场分布，可得到目标位置的系综平均值Ibg。如果在波前整形中只控制入射光的波前相位，那么多次实验得到的聚焦增强系数平均值和可控自由度N之间的理论关系为[15]

一般而言，入射光波前可控自由度N的大小取决于实验中空间光调制器的有效像素数目，即用多少像素来独立地调控所在位置的波前相位。在反馈式波前整形实验中，为了实现散射光的聚焦，可采用一个相机探测透射端目标位置的光强，并监测其随调控模式的可控相位KA的变化[15]：

其中，IA和ΦA分别表示来自入射光调控位置的散射光强度和相位，而IB和ΦB则分别表示来自其它非调控位置的散射光强度和相位。通过监控Itar随KA的变化，可以提取出最佳相位Km，其中最佳相位满足Km+ΦA-ΦB=0。随后，将该过程遍历每一个入射模式，即可获得一个结构化的相位图，并将其通过空间光调制器加载到入射光波前，则可实现散射光场聚焦。

本文根据反馈式波前整形理论，采用Matlab对散射光的聚焦过程进行了仿真。在反馈式波前整形过程中，背景光场IB和ΦB随调控位置的改变有细微的变化。为消除该变化所引入的误差，我们针对入射波前的N个单元进行了两轮相位测量，并得到一个优化的结果。由于每次独立的波前整形都改变了透射矩阵T，其对应着实验中对样品不同位置的散射光进行聚焦，因而每次得到的聚焦增强系数η各不相同。在仿真实验中，对不同N分别进行10 次独立的波前整形，从而得到聚焦增强系数的平均值ηˉ和标准差，结果如图2 所示。对这些数据点进行线性拟合，得到其斜率为0.81，与公式（4）的理论值π/4接近。

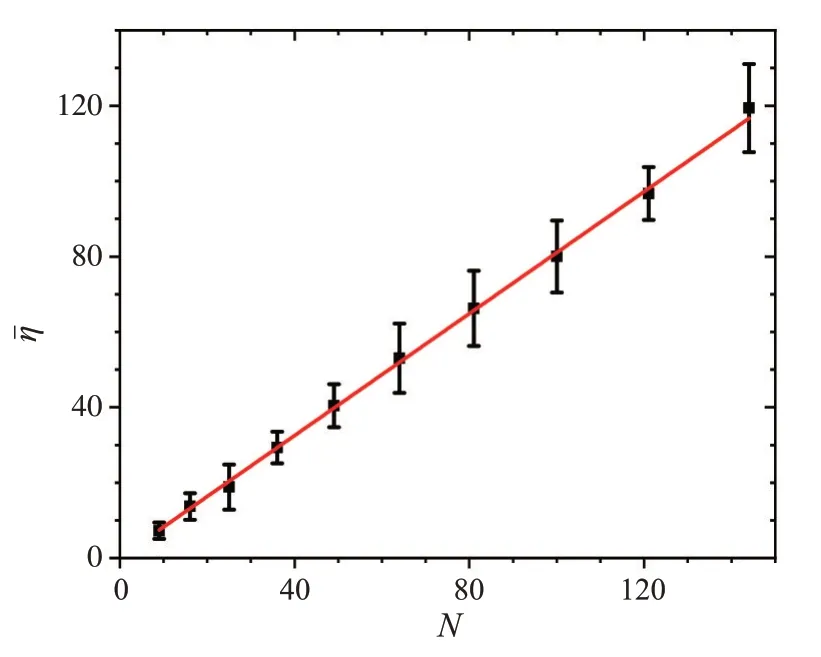
图2 无噪声下聚焦增强系数ηˉ与波前整形自由度N的关系

2 噪声对散射光聚焦效果的影响

前文的理论和仿真实验并没有考虑实际装置中的噪声，故与实际的实验结果差异明显。具体而言，在典型的波前整形装置中需要考虑空间光调制器的相位噪声、光场的探测噪声及样品去相干引入的噪声。基于此，我们分别对各种噪声的影响进行了讨论，以期明晰各种噪声对散射光聚焦的影响特点。

2.1 空间光调制器的相位噪声

空间光调制器具有大量的像素点，可单独控制入射光的波前相位。然而，空间光调制器的相位控制具有一定的误差。通常假设不同像素点的相位误差满足高斯分布：

其中，φ0表示预期的精确相位，φ表示空间光调制器实际加载的相位，σs表示相位误差的大小。

为了明晰该相位噪声对聚焦效果的影响，我们在仿真程序中引入了不同强度的相位误差，并保持其它条件一致，得到了如图3（a）所示的ηˉ随调控模式数N的变化情况。

图3 存在相位噪声时聚焦增强系数与波前整形自由度（a）和噪声强度（b）的关系

由图可知，随着相位噪声的增加，ηˉ与N之间依然保持线性关系，但是斜率变小。这意味着实际装置中的散射光聚焦依然可通过增加入射端的调控自由度来增强，但是聚焦效果较理论情况有一定减弱。随后，选定入射端调控自由度N为100，通过改变空间光调制器的噪声强度σs来研究增强系数ηˉ随σs的变化规律。如图3（b）所示，随着σs的增大呈现高斯线型衰减，即=+1。当σs趋于无穷时，聚焦增强系数趋近于1，表示无法实现散射光的聚焦。

2.2 光场的探测噪声

在反馈式波前整形中，探测器测量到的光强是推导优化相位的依据。然而，探测器测量的光强既依赖于入射模的相位变化，也存在着一些随机变化的噪声，噪声主要来源包括激光功率噪声和散粒噪声。激光功率噪声由激光器功率不稳定所引起，可模型化为一个高斯分布的随机噪声：

其中，Ic是激光的平均光强，I是激光的瞬时光强，σc是激光噪声的大小。

散粒噪声是激光的量子噪声，该噪声始终存在，其变化满足泊松分布[16]：

本文在探测信号中引入了功率噪声及散粒噪声。通过改变入射端调控的模式数N，可获得不同功率噪声下的聚焦增强系数如图4（a）所示，当仅存在散粒噪声而不存在功率噪声时(σc=0)随N的变化不再是线性增加的，而是出现饱和的趋势，其满足=η0(1-e-k(N-1))+1。这一变化规律在激光功率噪声的引入和增加时表现得更加明显。为了进一步确定激光功率噪声对聚焦增强系数的影响，本文研究了在N=100时随功率噪声强度σc的变化情况。如图4（b）所示，随着σc的增加指数下降，其满足=η0e-kσc+η1。由此可见，低功率噪声激光器在波前整形装置中极为重要。

图4 存在探测噪声时聚焦增强系数与波前整形自由度（a）和聚焦增强系数（b）的关系

2.3 样品去相干引入的噪声

在实际装置中，散射样品的结构随时间发生了改变，因而光场在样品中的散射路径也随之改变，称之为样品的去相干效应。这种去相干效应使得透射矩阵T在波前整形过程中发生了变化，导致散射光聚焦时的最佳波前发生变化。因此，在波前整形装置中，散射光聚焦效果必然受到样品去相干引入的噪声影响。为了定量研究去相干噪声对散射光聚焦的影响，可以假设在波前整形过程的每一次光强探测后，透射矩阵的所有矩阵元都单独受到了随机复数的干扰，并假设该干扰复数满足高斯分布[15]：

其中，ti是第i次波前整形的任意矩阵元值，δti+1是去相干引入的干扰项，σd是δti+1和ti标准方差比值。

如图5（a）所示，仿真实验控制了随机干扰项的强度，并通过改变入射端调控的模式数N，获得了不同条件下的聚焦增强系数随N的变化特点。当存在去相干时，随N的变化不再是线性增加，而是随N的增加出现饱和趋势，其满足=η0(1-e-k(N-1))+1。随着去相干效应的增强，聚焦增强系数明显减小。为了进一步确定去相干噪声的影响，我们探究了N=100时随去相干强度的变化规律，发现随着增加指数下降，其满足=η0e-kσd2+1。由此可见，动态无序介质的散射光聚焦更为困难。

图5 不同去相干条件下聚焦增强系数与波前整形自由度（a）和聚焦增强系数（b）的关系

3 各种噪声对散射光聚焦效果的综合影响

在实际光学装置中，散射光聚焦受到各种噪声的综合影响。具体而言，散粒噪声始终存在，激光功率噪声和相位噪声跟实验设备性能相关，而去相干引入的噪声和散射样品的特性有关。根据实际装置能够达到的实验参数，我们假设激光的功率噪声为1%，空间光调制器的相位噪声为1%，且激光的散粒噪声始终存在。针对一个静态无序介质和一个存在明显去相干的动态无序介质，分别研究散射光场聚焦特性随调控自由度N的变化。如图6所示，聚焦增强系数ηˉ随N的增加单 调递增，直至趋 于饱和，其满足=η0(1-e-k(N-1))+1。此外，样品去相干效应会减弱的值，并导致的提前饱和。当反馈式波前整形受到较大噪声影响时，虽然能够实现散射光场的聚焦，但是聚焦增强系数ηˉ大大降低。考虑ηˉ随调控自由度N的变化特征，噪声使得理论上的线性依赖转变为非线性饱和趋势，导致过度提高N并不能实现更强的聚焦。

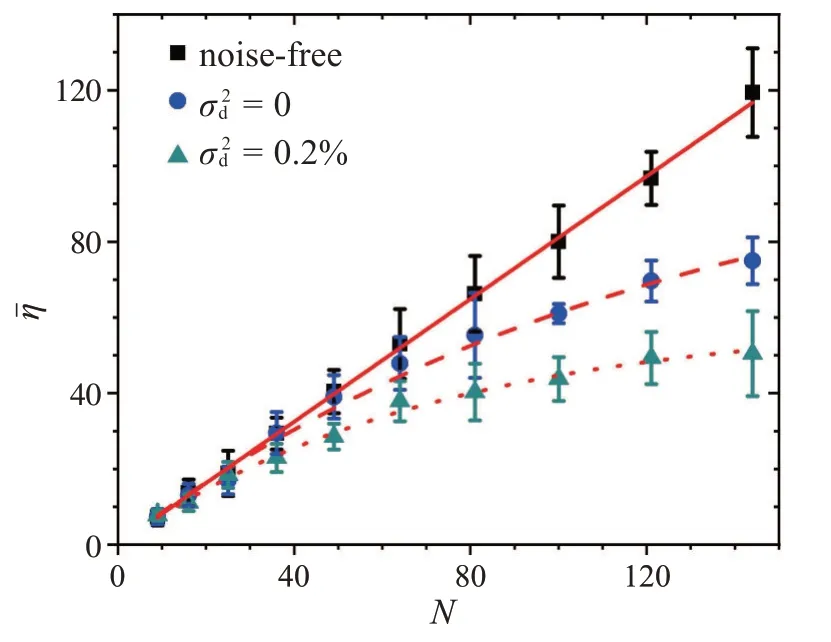
图6 各种噪声综合影响下聚焦增强系数与波前整形自由度的关系

明确各种噪声对散射光聚焦的影响，将促进学生更好理解散射光场聚焦在保密认证[17]、光计算[18]和光学成像[19]等方面的应用。以保密认证为例[17]，较高的聚焦增强系数意味着可减弱照明光场，并提高装置中单光子的概率，进而增强认证过程的安全性。显然，噪声的强弱在很大程度上影响着保密认证装置的安全性。为提高量子认证装置的安全性，有必要使用低噪声的激光、空间光调制器和探测器等关键设备。此外，用于认证的无序介质的时间稳定性也极为重要，去相干效应明显的无序介质只在有限的时间内完成安全认证。为提升教学效果，可进一步将噪声因素的考量延伸至迈克尔逊干涉仪和法布里珀罗干涉仪等其它典型干涉装置及应用中[11]，引导学生对噪声的影响进行讨论和分析。

4 结束语

本文以散射光聚焦为例，探讨了聚焦增强系数ηˉ和空间光调制器的相位噪声、探测噪声及去相干噪声的依赖关系。在光学课程教学中引入本案例，可以直观而生动地阐明噪声对多光束干涉效应的重要影响。通过结合保密认证等前沿光子学应用，可以加强对学生理论联系实际等工程创新能力的培养。此外，以本案例为契机，可将噪声因素的考量延伸至迈克尔逊干涉仪等其它典型干涉装置，以课堂提问和讨论等形式，引导学生思考噪声在相关应用中的重要作用，有助于启发学生从实际应用出发去理解光学理论，从而促进学生工程创新思维的培养。