基于新型燃料堆芯的不确定性分析研究

岳子腾,张 斌,刘天娇,王连杰,倪东洋

(1．国家电投集团科学技术研究院有限公司;2.国家能源核电软件重点实验室：北京102209;3．中国核动力研究设计院 核反应堆系统设计技术国家级重点实验室,成都610041;4.哈尔滨工程大学 核科学与技术学院,哈尔滨151100)

早期的核反应堆设计采用偏保守的程序和建模设计,虽可获得较大的安全裕度,确保反应堆的运行安全,但过于保守的设计会在经济性上抑制核电厂的发展。随着反应堆物理程序逐渐成熟和计算性能的提高,美国核管理委员会(Nuclear Regulatory Commission,NRC)提出了最佳估算评价方法,通过使用更真实的反应堆模型替代保守模型,来降低反应堆设计中的过度冗余,而最佳估算中重要一环是不确定性分析。不确定性分析可识别出对核设计关键参数最具影响的因素,以此来指导模型优化,获得更精准的安全裕度,改善核电厂运行的经济性。

不确定性会使得到的核设计结果与真实堆芯状态存在一定的差异,研究并量化这些因素对核设计关键参数的影响,对堆芯核设计有重要参考意义[1]。随着计算模型的持续改善,核数据和输入参数作为核反应堆物理计算的源头,是堆芯计算中最重要的不确定性来源[2-4]。

核数据是指在反应堆计算中所涉及的核素微观截面数据(吸收、裂变、散射和输运截面等)及裂变产物相关数据,是根据物理测量数据和与之对应的评价模型计算产生的,但在测量和计算中都会产生偏差,所以本身就存在不确定性。而核数据会直接用于输运方程的求解计算,并通过方程求解将不确定性传递到最终的计算结果中。本文中所用的核数据库为ENDF/B-VI。输入参数不确定性主要是指在反应堆中对状态参数的测量和燃料元件等堆芯部件的制造上所引入的偏差。在参数测量或元件制造时由于工具受限会带来测量偏差,导致电厂的实际运行参数和理论设计值之间存在偏差。这些输入数据反映到堆芯物理计算上为计算程序的输入参数,如燃料内径、富集度及堆芯压力等。

本文参考日本第三代实验堆JRR3(Japan research reactor NO.3)[5-6],研究了核数据和输入参数的不确定性对有效增殖因子keff的影响。针对核数据,首先开展了核数据对3维全堆芯keff的不确定性分析及对组件均匀化常数的不确定度计算;其次以组件均匀化常数库为基础,通过抽样方法,采用堆芯计算程序进行了全堆芯模拟,进行了核数据在两步法计算下的影响分析。针对输入参数,首先通过敏感性分析筛选出对keff影响较大的参数,然后使用参数统计法和非参数统计法等多种不确定性分析方法对备选参数进行量化分析。

目前,对新型堆的研究主要集中在解决由于燃料板流道间隙小、板间流速高导致的堵流事故或流致振动问题,而在不确定性分析方面研究较少,因此对新型堆开展堆芯物理计算不确定性研究具有重要意义。

1 理论模型

常用的不确定性分析方法有确定论方法和抽样统计法[7]。确定论方法通过对目标参数扰动进行敏感性系数计算,然后再结合协方差矩阵进行不确定度计算。根据对目标参数扰动方式不同,可分为微扰理论法和直接扰动法[8]。抽样统计法通过概率统计对输入参数进行不确定性分析计算[9]。除此之外,还有确定论和抽样统计相结合的混合法,该方法用于两步法堆芯计算不确定性分析,组件计算时采用微扰理论法,利用生成的少群截面协方差对少群群常数进行抽样统计用于堆芯物理不确定性分析。

本文采用基于微扰理论的不确定性分析方法进行核数据不确定性分析。该方法通过计算各参数的敏感性系数,结合协方差矩阵,用Sandwich公式计算得到不确定度。针对3维压水堆堆芯,采用蒙特卡罗程序进行3维堆芯的正向输运及共轭计算,进而获得敏感性系数,结合协方差矩阵计算获得核数据的不确定度。

两步法是堆芯计算的主流方法[10-12],核数据通过组件少群截面参数将不确定度传递到堆芯计算结果中。本文首先采用基于微扰理论的不确定性分析方法对少群截面参数进行不确定性分析;而后采用基于抽样方法对堆芯计算的模拟结果进行不确定性分析。图1为两步法计算策略的核数据不确定性分析流程。

输入参数是除核数据外的另一大堆芯模拟不确定性主要来源,涉及的参数包括了材料成分、几何公差和温度等。本文根据堆芯核设计主要输入参数及取值范围和分布函数,采用直接扰动法对输入参数进行敏感性分析,确定对堆芯keff影响较大的关键参数。通过对关键参数进行抽样,确定反应堆堆芯计算的输入参数样本空间集。通过两步法计算程序获得最终的堆芯计算结果后,对样本数据进行正态检验,若样本数据为正态分布,则选择参数统计法和非参数统计法进行分析,计算容忍区间;若样本数据不是正态分布,则选择非参数统计法进行分析,计算容忍区间[13-15]。图2为输入参数的不确定性分析流程。

图1 两步法计算策略的核数据不确定性分析流程

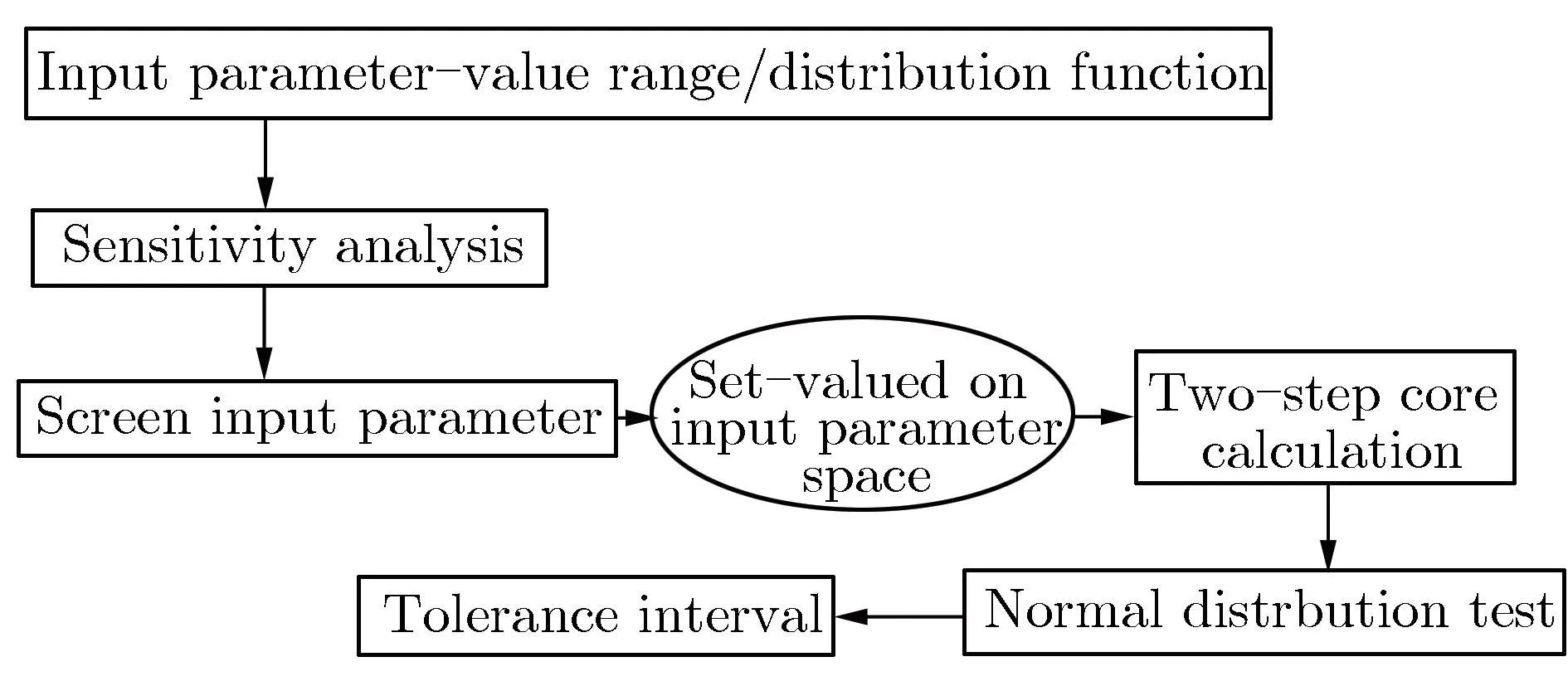
图2 输入参数的不确定性分析流程

2 数值计算与分析

JRR3是一个以轻水作为冷却剂,铍作为反射层的实验堆。堆芯由标准燃料组件、控制棒燃料组件和样品辐照孔道组件构成。在堆芯外围放置金属铍和重水箱作为反射层,整个反应堆淹没在水中。本文新堆型在JRR3堆的组件结构上对组件数量及组件高度等进行适应性修改。新型堆芯中含有2种标准燃料组件和含Hf吸收体的控制棒组件。燃料组件中的燃料板元件垂直并排插在Al制凹槽中固定,组成正方形横截面的燃料元件。标准燃料组件1含有20个燃料板,标准燃料组件2含有16个燃料板,堆内控制棒组件分为8组,堆芯活性高度为150 cm。反射层共分为3层,内层为金属铍,中层为重水,外层为轻水。图3为堆芯布置示意图。

图3 堆芯布置示意图

2.1 核数据的不确定性分析

2.1.1 核数据不确定性对keff的影响

通过SCALE软件包[16]蒙特卡罗计算模块直接对3维堆芯进行建模计算,核数据的不确定性分析采用确定论方法,通过输运计算和伴随(共轭)输运计算的结果分析得出。导致核数据对keff的不确定性来源如表1所列。由表1可知,核数据不确定性引起的3维堆芯keff的相对不确定度最大为0.540 6%。

敏感性系数是科学量化核数据不确定性对keff影响的重要参数,微扰理论法从中子输运方程出发,通过对输运方程和共轭输运方程扰动进行敏感性系数计算。影响全堆敏感性系数的核素反应主要包括：235U的平均裂变中子数、瞬发中子裂变份额、裂变截面及总截面慢化剂中H的总截面、散射截面及吸收截面等结构材料中Al的反应截面、反射层Be的散射截面238U的俘获截面和总截面。其中,235U的敏感性系数很高,尤其是平均裂变中子数和瞬发中子裂变份额,敏感性系数达到了0.99;238U裂变截面的敏感系数为0.47;至于H元素,则为10-1量级;238U的相关核素达到了10-2量级,较不敏感。因此,在核数据不确定性对板状燃料堆芯的影响中,最敏感的核素是235U和H。同时,结构材料和反射层材料的核素不确定性研究也对keff计算不确定性的研究有一定意义。

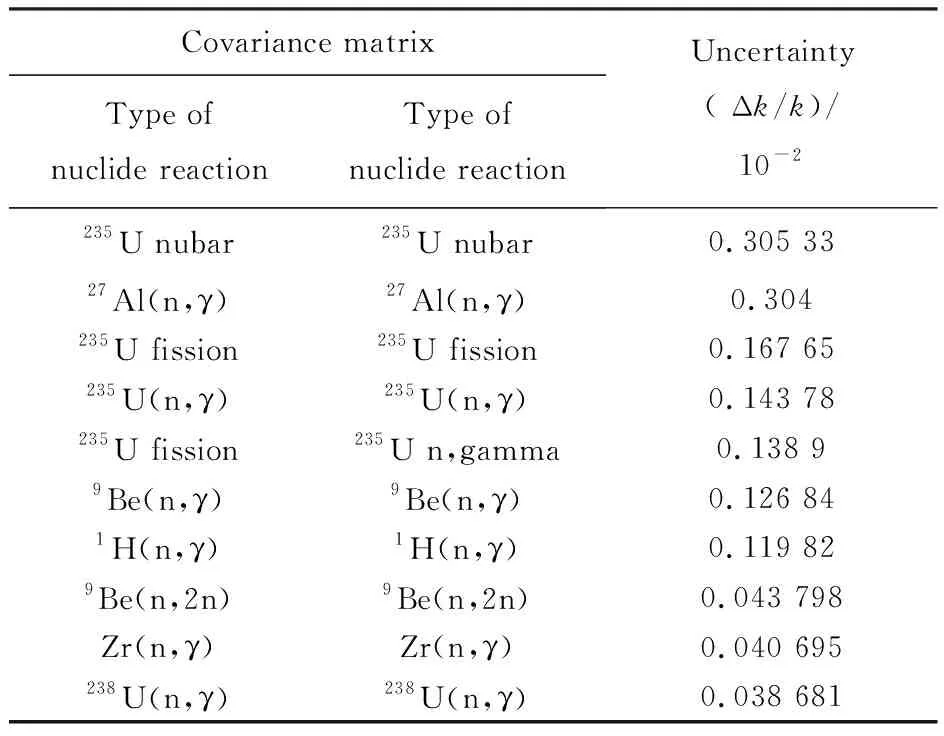
表1 导致核数据对keff的不确定性来源

2.1.2 核数据不确定性对组件群常数计算的影响

使用SCALE软件包中的TSUNAMI-2D模块分析核数据不确定性对群常数计算的影响及相关群常数不确定度在堆芯计算中造成的影响,作为核数据不确定性对两步法堆芯keff计算结果影响分析。堆芯计算采用4群的均匀化少群常数。

核数据引起的不同组件群常数的不确定度如表2所列。核数据不确定性引起的燃料组件keff的相对不确定度,燃料组件1为0.542 7%,燃料组件2为0.575%,反射层组件为0.570 9%,控制棒组件为0.538 6%。由此可知,燃料组件2和反射层组件中核数据不确定性对组件keff计算影响较大。与燃料组件2相比,燃料组件1成分增添了Zir-4合金,而反射层组件中Be核素的不确定性较大,这一点也与计算全堆芯敏感性系数中Be的敏感性系数较大相吻合。

由表2可知,与燃料组件群常数计算不确定度相比,反射层群常数计算不确定度较大。但燃料组件计算时须考虑裂变截面的不确定度,使二者在keff计算的不确定度上差距不大。核数据对高能群群常数计算不确定度比低能群偏大,这是由于高能区测量难度大,协方差数据比低能区高,进而导致后续计算结果高能群常数不确定度较高。组件不确定度导致的堆芯keff不确定度如表3所列。由表3可知,高能群相关截面不确定度对堆芯keff不确定度的影响较小,低能群(第4群裂变截面和吸收截面)不确定度对堆芯keff的影响较大,这是由于本次计算堆型为热谱水堆,热群核数据对不确定度的影响较大。

2.2 输入参数的不确定性分析

根据堆芯物理计算程序所需的输入数据,选取包壳尺寸、燃料尺寸、燃料密度、燃料温度、慢化剂温度、富集度及堆芯压力等18个备选输入参数进行敏感性系数计算,输入参数敏感性系数如表4所列。表4中,若敏感性系数为正,则表示输入参数与keff正相关;如果为负,则表示负相关。由表4可知,对keff影响最大的输入参数有富集度、燃料密度、燃料尺寸、包壳尺寸、铝密度(包壳)、慢化剂温度、反射层铍厚度、吸收体铪密度、吸收体铪厚度及反射层铍密度。富集度、燃料密度及燃料尺寸都是通过改变燃料含量来产生影响,由此可见,燃料含量对keff影响最大;堆芯压力和慢化剂温度都是通过慢化剂密度对keff产生影响,压力对密度的影响远比温度对密度的影响小,表现为keff对堆芯压力不敏感,对慢化剂温度较敏感。最终选取12个输入参数对keff进行不确定性分析。

表4 输入参数敏感性系数

在进行不确定性分析计算时,根据输入参数的取值范围和概率统计函数采用拉丁超立方法进行抽样,将N组抽样样本带入堆芯计算程序进行计算获得N组包含keff的样本数据,对样本数据进行正态分布检验,经检验符合正态分布,因此对输入参数使用参数统计法和非参数统计法计算keff的容忍区间。

非参数统计法对样本数据分布没有要求,是一种有序容忍限计算方法,可对样本进行容忍上下限计算。参数法要求样本数据符合正态分布,具体可分为总体均值方差均未知、总体均值方差均已知和总体均值未知方差已知3种情况下的不确定性计算方法。我国在《数据的统计处理和解释—统计容忍区间的确定》中制定了相关的容忍区间计算方法。当总体均值方差均未知时,要确定所需的置信水平1-α和覆盖率p。置信水平、覆盖率和容忍上下限的关系为：以1-α为置信水平确保总体落在容忍上限xL和容忍下限xU之间的比例至少为p。然后根据样本数量n、置信水平1-α和覆盖率p来确定容忍系数k(n,p, 1-α)。参数法计算的keff容忍上限可表示为

(1)

容忍下限为

(2)

经计算,输入参数对keff的相对不确定度为0.20%。各种不确定性分析方法的容忍区间如表5所列。由表5可知,各种方法的容忍区间计算结果相近。从过程中来说,参数法可对所有输入参数同时进行扰动计算,但对输出参数的分布要求较为严格,必须为正态分布,所以使用参数法时要对输出数据进行正态检验,若输出数据不为正态分布时则不能使用。

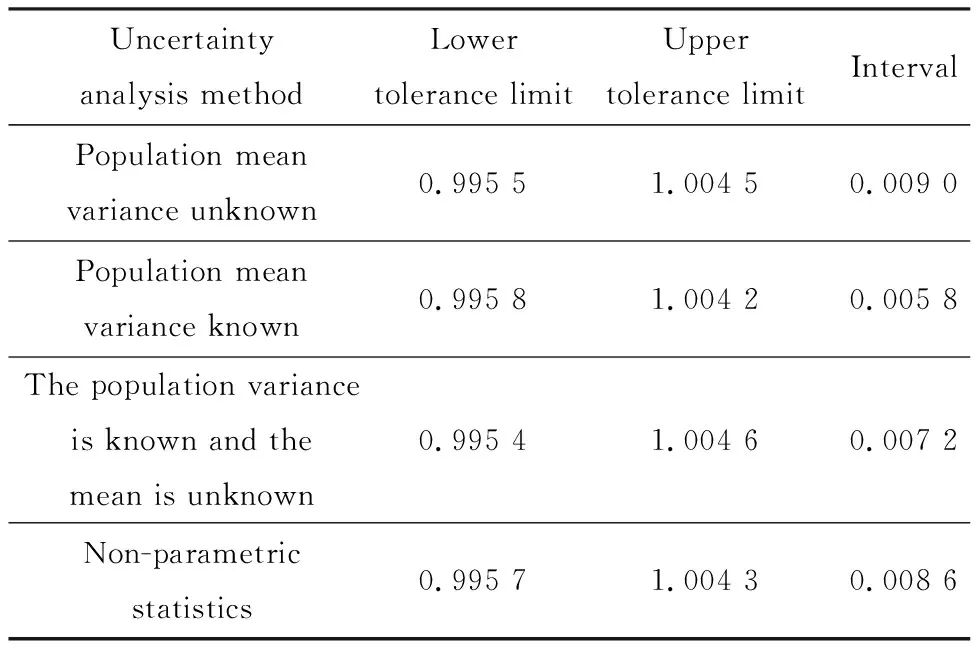
表5 各种不确定性分析方法的容忍区间

相比之下,非参数统计法对数据的分布没有要求,分析流程简单,当确定样本数量时,数据的容忍上下限即为样本数据的最大值和最小值,且与参数统计法计算结果相近。

3 结论

本文参考日本第三代实验堆JRR3,采用确定论方法和混合法量化分析了核数据对板状燃料堆芯计算不确定度及影响因素,使用非参数统计法和参数统计法等多种抽样统计不确定性分析方法对板状燃料堆的keff进行不确定性分析。结果表明：核数据对堆芯keff的相对不确定度为0.540 6%,该结果主要来源于核数据对燃料组件和含有Be元素的反射层组件的计算不确定度;在核数据对堆芯keff的计算中,较为敏感的核素反应是235U的平均裂变中子数和瞬发中子份额,其次为H的散射截面,不确定度较大的为235U平均裂变中子数和Al的(n,fission)反应截面。核数据的不确定度在高能区较大,但对新型燃料,仍是由低能群群常数计算的不确定度主导影响反应堆堆芯keff计算的不确定性;在输入参数对堆芯keff的计算中,输入参数对keff的不确定度为0.20%,非参数统计法与3种参数统计法计算结果相近,keff对富集度、燃料密度、燃料尺寸和包壳尺寸较敏感。