压杆式冲击波反射压力测试技术研究进展
杨 军,张德志,刘文祥,史国凯,张 敏,徐海斌,马艳军,李 焰,王 昭,惠海龙
(强脉冲辐射环境模拟与效应全国重点实验室;西北核技术研究所:西安710024)
炸药在极短时间内完成化学反应,瞬间将自身所具有的化学能转换为热能,使爆炸产物瞬间被加热到几千开的高温并产生数吉帕的压力,高温和高压驱动气体产物迅速向周围膨胀做功,高速膨胀的高温高压气体犹如活塞推动周围的介质向外运动形成冲击波。冲击波以数倍于声速的速度向外传播,作用于它遇到的任何障碍物,可能产生灾难性的损坏。
一方面,在新型武器装备和爆破器材的研制过程中,爆炸产生的冲击波通常作为重要指标贯穿于方案设计、研制生产和考核定型整个过程。装备定型试验中一般会安排多发静态爆炸实验,测量其产生的冲击波等毁伤元的特性参数,考核是否满足指标要求。
另一方面,防护工程则关注爆炸产生的冲击波、射流及破片等对结构,如在坦克等装甲车的主装甲、舰船结构、机库及重点建筑物等的破坏作用。近年来,随着全球反恐和安保的需求日益旺盛,原来只有大使馆、前沿作战基地和总部等高价值建筑物才考虑的抗爆炸设计,越来越多地出现在民用设施中[1]。如何准确量化作用在建筑物及结构体上的爆炸载荷成为抗爆炸设计的难点,虽可采用半经验预测或有限元计算等方法确定最简单几何情况下的载荷,但这些方法在极近距离爆炸事件等复杂情况下的适用性存在一定的疑问[2-3]。
爆炸在工业和国民经济建设中的应用也存在类似问题,如在矿山爆破、定向爆破及建筑爆破等过程中,炸药爆炸产生的一部分能量仍以冲击波形式释放。另外,近年来国内发生了多起安全生产事故,爆炸产生的冲击波及产物扩散对人员、环境造成了极大的危害。在这类爆炸事故中,爆炸冲击波是重要破坏因素,对其开展研究可反推爆炸当量及查找事故原因,为制定安全生产规章制度提供技术支撑。
在上述武器装备、防护工程和爆破工程的研究中,近距离爆炸产生的冲击波压力均在数百兆帕以上,且上升沿为数微秒量级,对冲击波压力传感器和测量系统提出了很高的要求。
1 国内外技术现状
完整测量和记录冲击波压力波对深入研究炸药特性及其对效应物的作用具有重要意义。经多年发展,目前,冲击波压力传感器及测量技术主要以压电式压力传感器和压阻式压力传感器为主。另一类压杆式压力传感器则主要在研究机构中应用较多,市售成品较少。在炸药爆炸近场测量实验中,冲击波压力幅值大、上升快、脉冲短及电磁干扰严重,要求传感器量程大、高频响应和抗干扰能力强。压电式压力传感器的晶体在大量程压力作用下易损坏,且较易受电磁辐射影响。压阻式压力传感器对光辐射[4]和热辐射敏感,信号中干扰较大,量程较低。压杆式压力传感器以压杆为弹性敏感元件,实现压力到应力、应变等力学量的转换,再通过电学测量技术将力学量转换为电信号,突出特点是量程大、敏感元件不易损坏,能应用于炸药近场冲击波参数测量。该传感器定制化程度高,用量较少,尚无批量生产的成熟型号,国内外主要是从事爆炸相关的研究机构和高校按照自身测试需求设计制作。本文将简要介绍压杆式压力传感器的发展历程、压杆中应力波弥散效应及校正方法研究的国内外现状。
1.1 压杆式压力传感器的发展历程
1914年,Hopkinson[5]最先提出采用细长圆柱杆测量冲击波压力,所以一般称压杆式压力传感器为Hopkinson pressure bar (HPB)。1921年,Robertson[6]和Landon等[7]在此基础上进行了改进优化。在该优化方案中,从杆尾部切出一定长度的小段作为飞片,将飞片涂抹凡士林后粘回到杆末端,当冲击波或子弹作用在压杆一端时,杆中激发应力波并沿杆传播,压缩波可通过凡士林涂层传播至飞片,在飞片末端面反射为拉伸波并反向传播;当涂层中压缩波幅值小于拉伸波幅值后,涂层在拉应力作用下破裂,飞片飞离压杆末端;飞片从开始受压到分离的时间约为两倍飞片长度除以弹性波速,该时间为飞片所受冲量的积分时间。测量飞片的速度和质量计算得到动量,即为飞片中应力在积分时间内得到的冲量。再根据已知的积分时间,可由冲量计算出积分时间内的平均应力。因此,该方法不能给出压力的任何时间特性,只能给出该时间内的平均值。可采用不同厚度的飞片进行多次实验,计算不同积分时间内的平均压力,确定压力的时间历程。但该方法需大量实验,且须保证多次实验的重复性和一致性。
1948年,Davies[8]率先采用平板电容、柱形电容和双束阴极射线管示波器测量压杆端面位移和径向位移曲线,经计算获得压力历程曲线,解决了Hopkinson[5]方案无法通过单次实验获得压力曲线的难题。图1为Davies使用的平板和圆柱电容器。
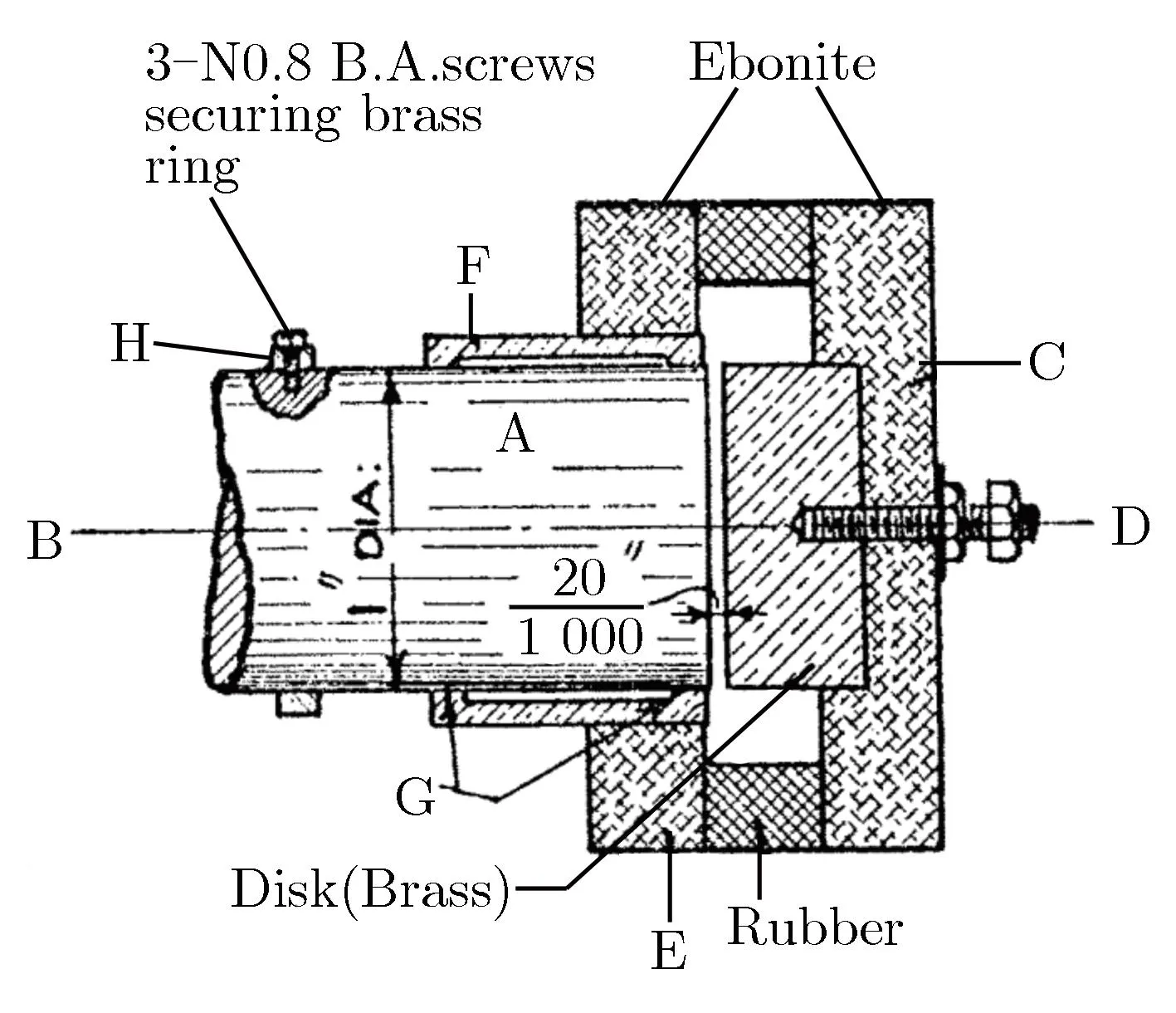
(a)Parallel-plate condenser
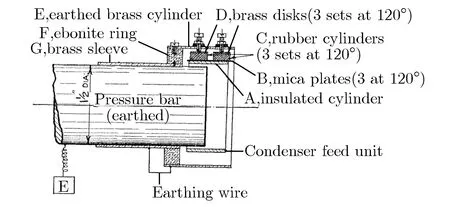
(b)Cylindrical condenser
1966年,Hauser[9]采用应变片测量入射杆和出射杆表面的轴向应变,经过计算得到夹持在两杆中间材料的动态力学性能。图2为Hauser使用的实验装置和仪器。与此类似,压杆表面黏贴金属应变片或半导体应变片测量轴向和环向应变,反推计算得到承压端面的冲击波压力波形的方法已成为HPB中的标准测试技术[10-12]。
1966年,Jones[13]使用直径为3 mm的铍杆研制了压力传感器,敏感元件选用PZT晶体,两根场为100 mm的铍杆将晶体粘接在中间,在激波管中实测获得传感器阶跃响应上升沿为0.54 μs。1996年,Dick等[14]等利用压杆成功测得爆炸近区的冲击波压力,峰值达到2.4 GPa。

图2 Hauser使用的实验装置和仪器[9]
进入21世纪以来,压杆式压力传感器作为一种大量程压力传感器仍然活跃在爆炸与冲击领域,在近距离爆炸冲击波测试中发挥着不可替代的作用。英国Sheffield大学在HPB方面的研究最为突出,2000年以来发表了14篇以上文献对压杆的传输特性、校正理论和实验应用开展了详细的论述。2000年,Tyas等[15]在压杆表面黏贴轴向和环向应变片,将实测的轴向、环向应变信号的幅频谱相除后与理论结果进行对比分析,验证了杆中应变在径向上是非均匀分布的。Tyas[16]采用数值计算方法研究了集中载荷作用下压杆的响应,为评估频域色散校正方法应用于集中载荷时的精度提供了思路。Tyas等[17-19]研究了包含径向分布不均匀性校正因子的校正方法,实现了一阶模式下幅值相位的完全校正。2014年,Clarke等[20], Rigby等[21]采用压杆阵列研究了浅埋炸药爆轰载荷空间分布的测量方法。2015年,Rigby等[22]采用压杆测量了远场爆炸冲击波入射角对测量结果的影响。Rigby等[23]采用Clarke等[20]类似的装置研究了近场爆炸产生的空气冲击波参数的时空分布。2016年,Tyas等[24]研究了炸药爆轰产物快速余燃对近场爆炸冲击波波形的影响,实验结果表明,余燃影响了冲击波波形的细节,且在空间上具有方向性。2018年,Rigby等[25]综述了HPB数据分析技术的研究。2019年,Rigby等[26]研究了近场爆炸冲击波作用在平板上的冲量分布和瞬态变形。2020年,Barr等[27]采用有限元方法研究了杆中多模弹性波的能量分配关系,并进行了多模校正算法研究。2020年,Rigby等[28]把利用高速摄像间接测量的压力分布与压杆直接测量的压力分布进行了比较,结果表明,在反射压力分布方面,间接测量的压力分布与直接测量的压力分布具有良好的定性一致性,与峰值反射压力有较好的定量一致性(小于最大记录值的10%)。该研究使用了17根压杆组成的阵列同时测量爆炸产生的冲击波,测试结果可表征冲击波在空间的分布规律。图3为爆炸载荷特性实验装置的原理框图。

(a)Side view
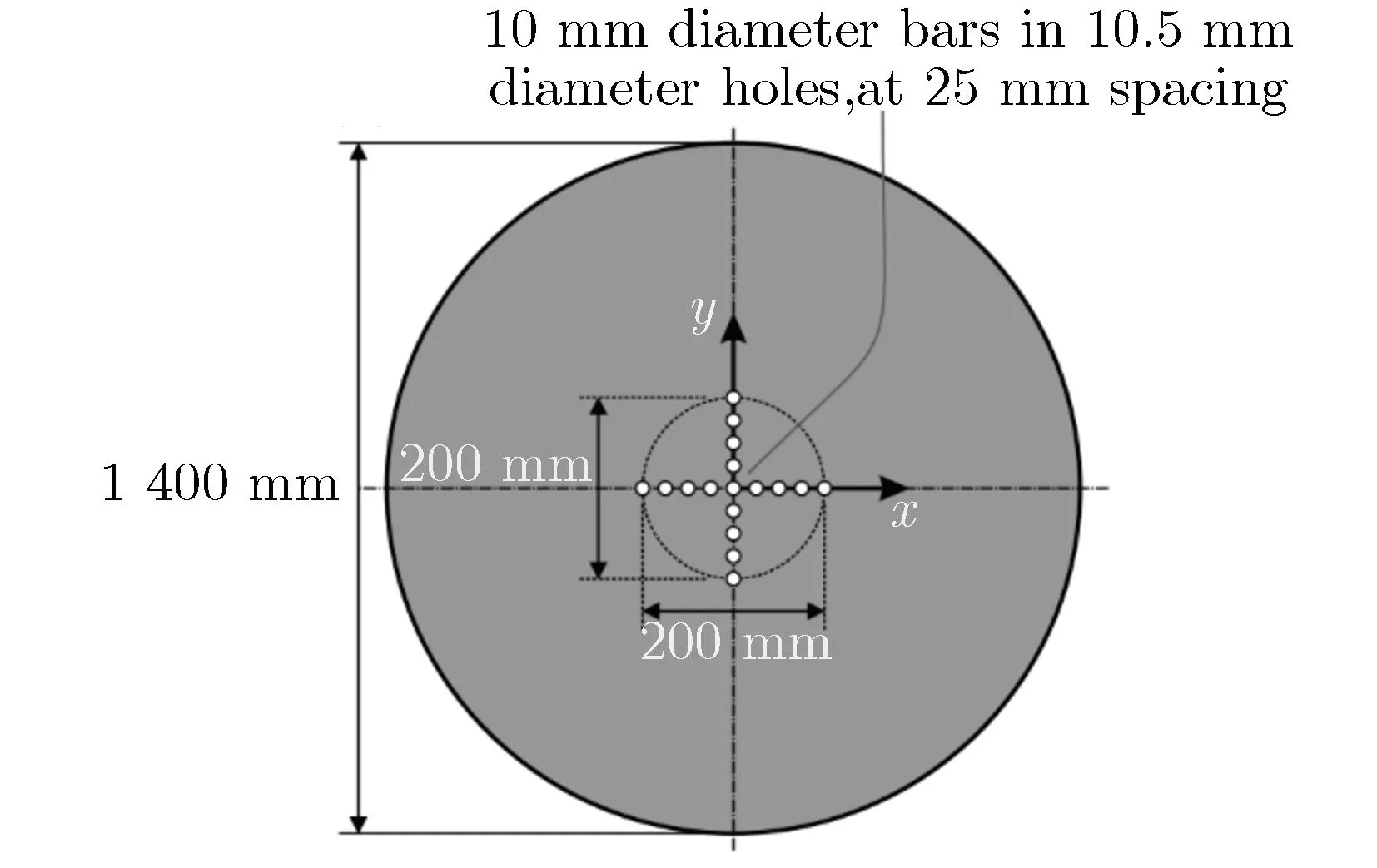
(b)Top view
南非开普敦大学也在此方面开展了多项研究[29-31]。2016年,Cloete等[29]在弹道摆的中心安装压杆,同时测量爆炸产生的冲击波反射压力和冲量。图4为Cloete设计的同时测量冲击波反射压力和冲量的装置。

图4 Cloete设计的同时测量冲击波反射压力和冲量的装置[29]
1.2 压杆中应力波弥散效应
与压电式和压阻式压力传感器相比,压杆式压力传感器具有量程大及敏感元件不易损坏等优点,能应用于炸药近距离冲击波参数测量,但一直以来始终面临两个主要难题,包括:(1)压杆中轴向弹性应力波在传播时因横向惯性效应发生弥散,即不同频率的应力波相位传播速度不同,导致测量元件处测得的信号与杆承压端面实际载荷在波形上并不一致;(2)杆中各力学参数(如应变和粒子速度等)在半径方向上分布不均匀。尽管在前端加载均匀分布的载荷,传播一定距离后仍由于弥散效应导致分布不均匀,表面黏贴应变片测得的应变与杆横截面上的平均应变存在差异。为解决这两个问题,众多学者开展了压杆中轴向弹性应力波弥散效应及校正方法的研究,并持续至今。目前大部分杆中轴向弹性应力波弥散分析和校正方法的理论基础均为Pochhmmer-Chree(P-C)理论。Pochhammer[32]求解了无限长、均匀、各向同性、线弹性且无阻尼圆柱杆中轴对称单频正弦载荷的运动方程,Chree[33]独立求解了该方程,因此该方程被称为P-C频率方程(简称“P-C方程”),该理论也称为“P-C理论”。Love[34]详细描述了该方程,但由于形式复杂,求解较为困难,并未有学者给出解析解。
1941年,Bancroft[35]首次采用数值计算方法求解了P-C方程,获得了不同泊松比下圆柱杆中轴向弹性应力波的一阶相速度曲线和位移沿截面半径方向的变化规律。图5为不同泊松比下归一化相速度v/v0随D/L的变化关系(其中:D为压杆直径;L为压杆中单频应力波的波长)。

图5 不同泊松比下归一化相速度v/v0随D/L的变化关系[35]
由图5可见,杆中轴向应力波传播速度是变化的,并非1维应力波初等理论给出的传输速度为常数。该方法同样也可应用于扭转波和弯曲波。同时,Bancroft[35]指出P-C方程存在无穷多组解,即理论上杆中应力波以无穷多传输模式中的一种或几种组合进行传播,事先无法预知。
1948年,Davies[8]利用设计精巧的实验装置测得了杆自由端面的轴向平均位移曲线和径向平均位移曲线,经过一定的计算得到了压力曲线。在实验上验证了P-C方程的解,发现基础传输模式下应力脉冲中高频分量的群速度低于低频分量,所以主脉冲后部随着高频振荡。Davies[8]还深入研究了杆中力学参数随半径的变化规律,该规律成为径向不均匀性校正的理论基础。Bancroft[35]和Davies[8]研究的重要意义在于为后续学者提供了研究杆中弹性波弥散效应和分布规律的具体思路和方法,成为压杆研究领域的经典文献。
1954年,Curtis[36]第一次在实验中观察到二阶模式弥散,试验中压杆安装在激波管末端,压杆前端面受激波管产生的阶跃压力作用,杆中多处黏贴应变片以测量表面轴向应变。不同位置的应变片所测压力波形存在差异,在时域上开展深入分析后发现,该波形中同时存在一阶和二阶模式的弥散效应。1957年,Oliver[37]进一步提供了二阶模式弥散效应的实验证据。1978年,Yew等[38]利用快速傅里叶变换方法(fast Fourier transform,FFT)分析了杆上两测点的应变波形及相速度,如图6所示。
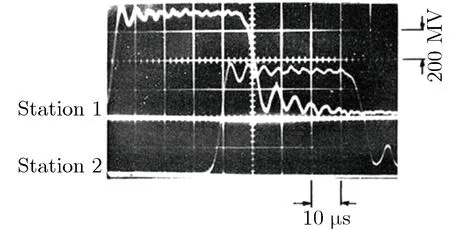
(a)Waveforms
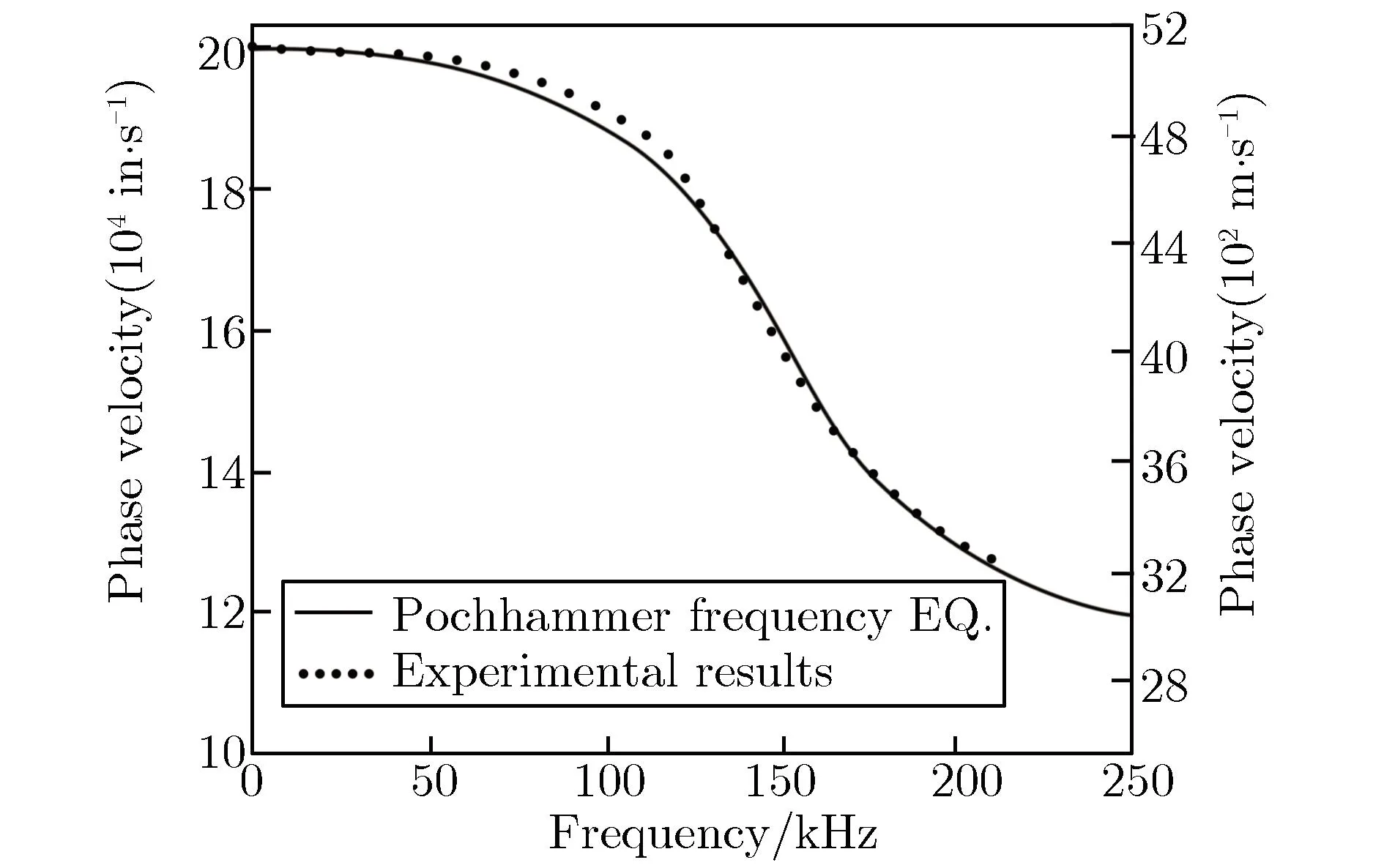
(b)Phase velocity
由图6(a)可见,轴向应力波各频率分量的相速度与P-C方程一阶传输模式的理论值几乎一致,证明有限长度的压杆依然可用P-C理论来进行研究。
2000年,Tyas等[15]首先基于P-C理论研究了瞬态压缩脉冲沿压杆纵向传播时轴向应变和环向应变沿杆的分布规律。在压杆表面黏贴轴向应变片和环向应变片测量应变波形,将二者进行傅里叶变换后对频谱进行相除运算,再将获得的频谱比值曲线与理论曲线进行对比,发现二者在一定频率范围内是吻合的,实验验证了轴向应变在压杆横截面上是非均匀分布的。
1.3 弥散校正方法研究
第1.2节所述理论分析和实验研究表明,爆炸冲击波作用在压杆前端面后会在杆中激发快上升沿的轴向弹性应力波并沿杆传播。由于横向惯性效应,杆中应力波会按照一阶或多阶模式向前传播,各阶模式下具有不同的相位传播速度,不同频率的应力波传播至敏感元件的时间不同,因此波形会发生失真。另外,杆中力学参数沿径向非均匀分布,在压杆表面测量的应变并不代表横截面内的平均应变,采用表面应变进行推导会导致偏差增大。因此如何将压杆上敏感元件测得的信号通过一定的计算方法校正横向惯性引起的弥散和非均匀分布成为研究的重点。
上述校正方法研究分为基于FFT的一阶频域校正方法、基于P-C理论的一阶幅值-相位校正方法和高阶模式校正方法3个阶段。
(1)基于FFT的一阶频域校正方法,该方法只校正因相速度不同而导致的相位偏差。1983年,Gorham[39]和Follansbee等[40]独立地开展了一阶频域校正方法的研究。用P-C方程的一阶传输模式和传感器与承压端的距离计算获得不同频率轴向应力波的相位偏差,并将相位偏差叠加到实测信号频谱上,反傅里叶变换得到的信号具有较好的上升沿和更小的弥散振荡。这种一阶频域校正方法在很长时间内占据主导地位,已被广泛应用于实际的压杆测试工作中[41-43]。
(2)基于P-C理论的一阶幅值-相位校正方法,针对压杆横截面上应变分布不均匀和相位偏差进行校正,但只涉及一阶传输模式。作为横向惯性效应的另外一面,力学参数在横截面上径向非均匀分布获得的关注较少,但黏贴于压杆表面的应变片测量的是表面应变,这种非均匀性分布导致的测量偏差在爆炸产生的高频信号中是不可忽略的。2001年,Tyas等[19]基于P-C理论获得压杆横截面应变不均匀性和应力应变的动态关系,计算了一阶传输模式下从表面应变到截面平均应变,再到截面平均应力的频率相关的振幅转换系数。Tyas等[19]还指出采用高阶传输模式的数据同样可计算出类似的幅值转换系数。2005年,Tyas等[18]将该系数作为幅值校正和Gorham[39]的相位校正进行联合计算,获得了较好的校正效果。这两篇文献成为杆中力学参数径向非均匀分布校正的重要文献。
(3)第一和第二阶段发展的校正方法主要针对一阶传输模式,随着杆上测量元件和记录设备的改进,更多的爆炸载荷研究中观测到高阶传输模式,因此针对高阶传输模式弥散效应的校正方法研究成为近年来研究的重点。1989年,Gregory等[44]用最小二乘积分式分析P-C方程,确定了各频率成分在各传输模式之间的能量分配比例。2004年,Puckett[45]采用该方法提出了一种柱形杆中波传播的解析模型,但实验结果表明该解析模型并不能预测波长小于杆直径的频率成分,尤其是在杆中激发了高阶传输模式的情况下。1993年,Lee等[46]提出了用矩形窗傅里叶变换算法分析压杆中信号,获得各频率成分到达测点的时间和相位偏差,因此获得了各频率成分的相速度。在此基础上,1995年Lee等[47]采用高斯窗傅里叶变换分析了水中爆炸冲击波的压杆数据,获得时间相关的傅里叶系数。将该系数绘制在时间、频率为自变量的功率谱图中,显示了各理论传输模式的明确证据,认为在特定时刻,群速度最快的传输模式在能量上占主导地位,其余部分不作考虑,所有频率成分只在群速度最快的模式下传播,由此构造出群速度随频率变化的单值函数,并推导出相应的相速度曲线,利用该相速度曲线对压杆信号进行校正。但该方法认为群速度最快的模式在能量上占主导地位的假设并不一定成立,且构造出的相速度曲线存在多个不连续点。2011年,Husemeyer[48]采用Lee等[47]的方法进行了数值模拟研究,结果表明群速度低的传输模式所占能量并不足够小到可忽略。2020年,Barr等[27]提出了一种前四阶传输模式校正方法,首先,采用数值计算模型计算单个和多个传输模式下的应力在横截面上的分布,并与理论模型进行对比,验证了数值计算模型的正确性;其次,利用该数值计算模型研究各传输模式之间能量分配的模式分配因子;最后,利用该模式分配因子将Tyas等[19]提出的方法扩展到前4阶,形成了考虑各模式间能量分配的校正算法。
尽管上述学者对高阶传输模式弥散效应进行了研究,但对给定频率分量在给定模式下传播的幅值(单一模式除外),目前还没有公认和经过验证的方法来估计。现有工作还未能分离各传输模式及确定各模式的能量占比,无法开展多模传输情况下的精确校正。然而,安全经济的抗爆结构设计、近距离炸药爆炸研究和爆炸数值模型验证等研究都须对爆炸载荷产生的高阶传输模式的弥散效应进行精确校正。
1.4 国内研究现状
与国外在压杆测压系统设计、结构优化和校正方法分析等方面开展的工作相比,国内的研究较少,主要集中于少数单位,研究重点为系统构建及影响因素分析等方面。
1986年,范良藻等[49]将利用短压杆和物理气象沉积(physical vapor deposition,PVD)薄膜研制的上升时间为20 ns的传感器应用于激波管实验,获得了较为理想的结果,图7为范良藻等研制的激波管标定用压力传感器结构图。该传感器主要用于标定激波管中的阶跃压力信号,因杆长度较短并不能应用于正压作用时间较长的爆炸冲击波测量。
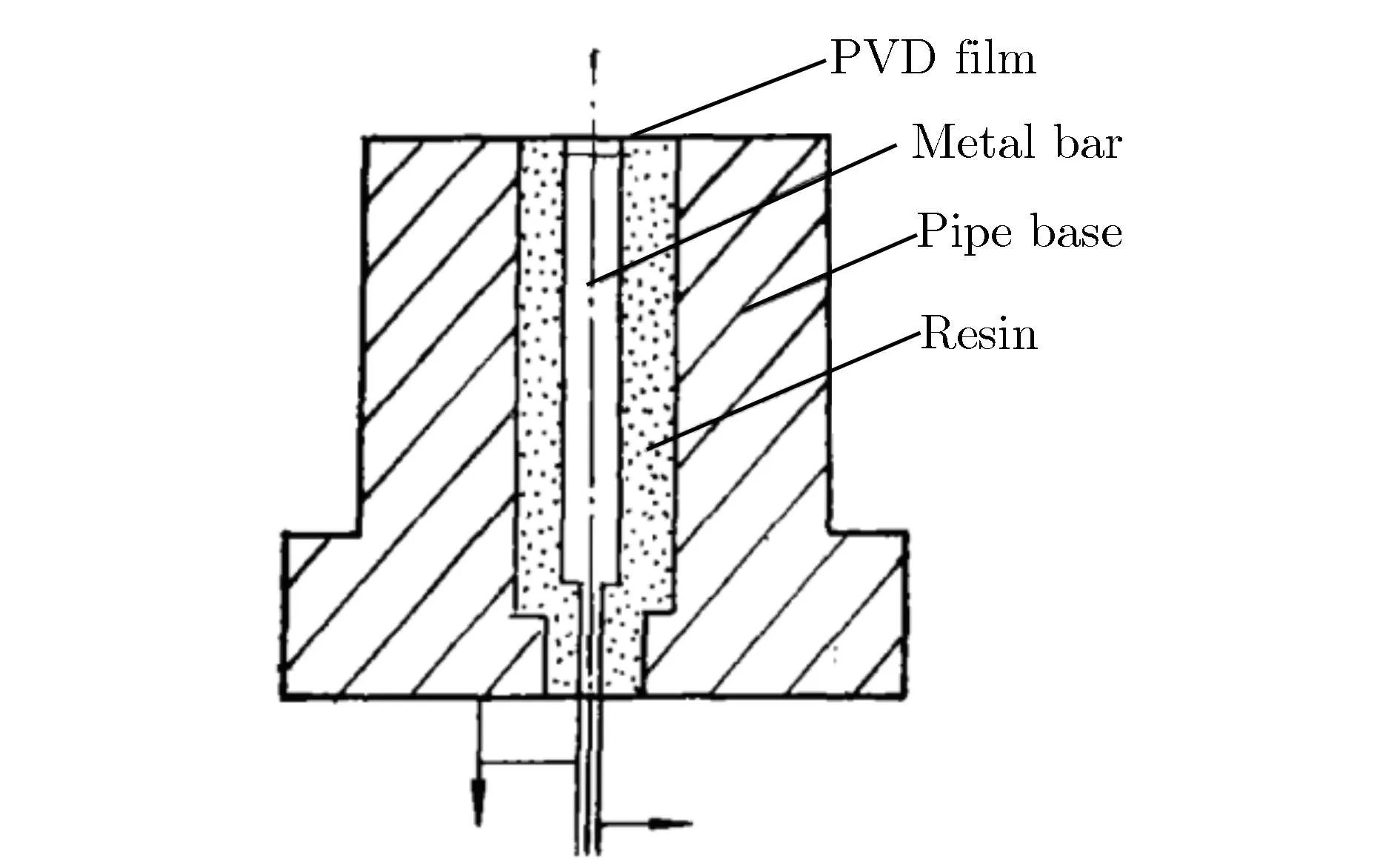
图7 范良藻等研制的激波管标定用压力传感器结构图[49]
2012年,宜晨虹等[50]用数值模拟的方法对应变式压杆压力传感器系统进行仿真,研究压杆的截面变化对测试结果的影响,数值模拟了不同上升前沿的梯形脉冲和三角形脉冲条件下变截面压杆的响应偏差。与非变截面压杆相比,变截面压杆的应力波幅值和波形均发生了很大变化,无论梯形脉冲还是三角形脉冲,变截面压杆的应力波幅值都要降低,证明压杆应为等截面杆,不能加工成台阶截面用于限位。2014年,宜晨虹等[51-52]利用数值模拟的方法分析压杆表面划痕在不同特征压力脉冲下对测试结果的影响,研究结果表明,压杆表面的划痕(宽为2 mm,沟槽深为0.5 mm)对测试结果影响很大,脉冲上升前沿越小,对测试结果的影响就越大;又研究了3种不同材料压杆对测试结果的影响,研究结果表明,铍压杆对测试结果影响较小,铝合金压杆影响最大。整体上看,该3项工作采用有限元数值模拟来开展研究,并未涉及实际的系统设计和实验验证,得出的相关结论具有一定的指导意义,但理论分析较弱。如铍压杆(泊松比为0.05)优于铝压杆(泊松比为0.33)的主要原因是泊松比小,所以横向惯性效应小,进而弥散较弱,而宜晨虹等只是对数值模拟得出的结果进行了表象的描述。
2 西北核技术研究所研究现状
西北核技术研究所最早推动开展应变式压杆压力传感器的研究。2006年以来,胡永乐[53]、石培杰[54]、王长利[55]分别介绍了应变式压杆压力传感器测量空气冲击波反射超压的原理及方法、测试仪器系统的构成及工作原理,并应用于爆炸容器壁面所受载荷的测量,图8为西北核技术研究所研制的应变式压杆压力传感器。张德志等[56]对应变式压杆压力传感器系统进行了分析和计算,频率响应约为115 kHz时,对直径为8 mm的钢杆使用电阻应变片的可测量下限为3.6 MPa。邹虹等[57]针对应变式压杆测试系统在冲击波超压测量中存在动态响应不足的问题,建立了激波管校准平台,采用系统辨识建模和动态补偿的方法,将时域分析和频域估计相结合,设计了一种动态补偿滤波器,改善了压杆测试系统的动态特性,使频带展宽,响应时间变快。
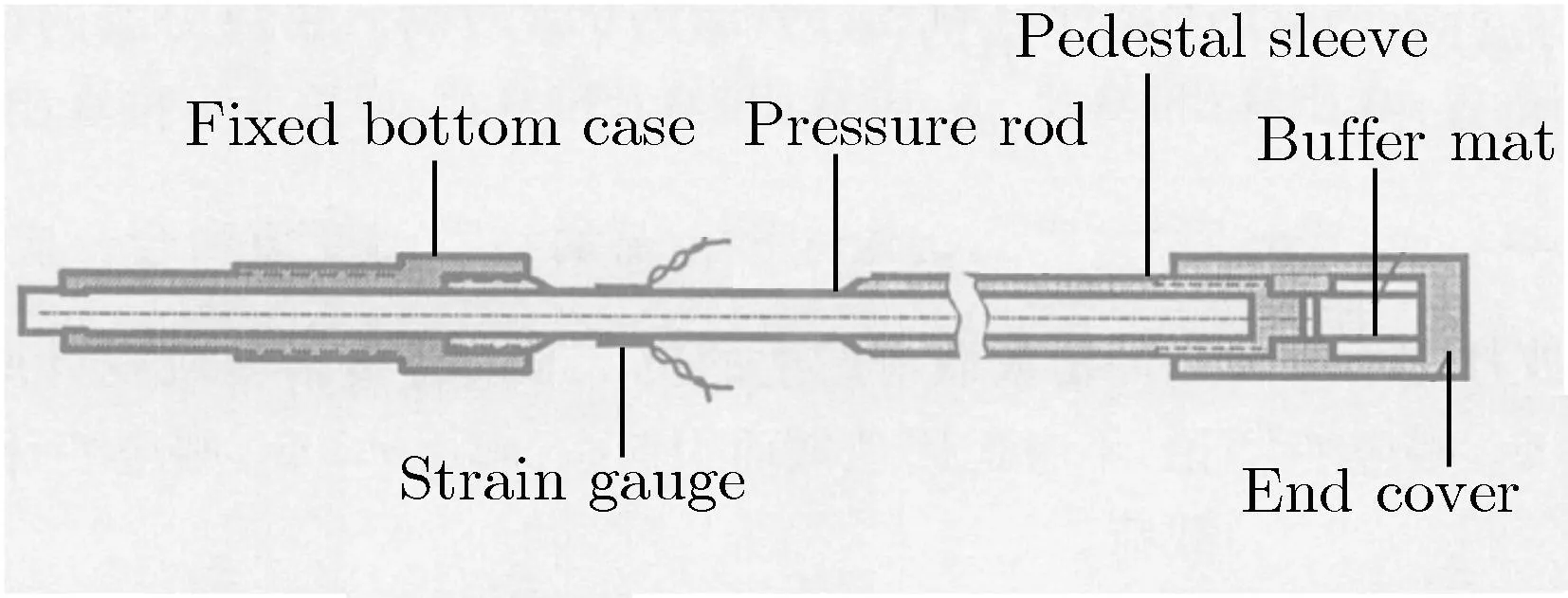
图8 西北核技术研究所研制的应变式压杆压力传感器
2016年,王昭[58]针对应变式压杆测压系统中长电缆频谱带宽不足问题,提出了一种系统整体补偿方法,利用电路仿真软件计算补偿电路的带宽,迭代完成辅助设计和优化。现场测试结果表明,加入补偿电路后,系统带宽由160 kHz提升至600 kHz,满足应变式压杆测压系统的带宽需求。
2017年,杨军[59]为在强电磁干扰环境下测量爆炸冲击波的壁面反射压力,首次将光子多普勒测速仪(photonic doppler velocimeter,PDV)与压杆相结合,设计了一套冲击波反射压力测试系统,如图9所示。对该系统进行了响应特性、有效测量时间和测量下限分析,结果表明,该系统频响低于杆表面黏贴的应变片电测系统,测量下限和抗电磁干扰能力优于应变片电测系统。该系统在典型球形炸药爆炸实验中实测冲击波反射压力峰值为463.5 MPa,上升沿为5 μs。

图9 冲击波反射压力测试系统[59]
2018年,李焰等[60]在直径为4 mm的压杆静态和动态标定实验中观察到弯曲波及其对波形平台造成的畸变,给出了应变片黏贴位置偏差对测试结果影响的估算公式,分析研究不同附加质量情况下的动态波形特征。
2020年,杨军等[61-62]继续对图9所示系统进行深入研究,对多种材料开展静、动态拉伸和动态压缩试验,获得了弹性模量、泊松比和动态强度等参数,优选材料制作压杆,将系统量程提高至3 GPa量级;采用数值方法求解P-C方程,获得了前4阶轴向应力波传输模式的相速度曲线、群速度曲线和归一化频率随传播时间的变化关系;基于杆中各力学参数径向分布函数,推导了压杆自由面中心点轴向速度到杆承压端平均应力之间的转换系数公式;提出了杆中轴向弹性应力波传输模式分析方法和局部相位-幅值联合校正算法,用于将压杆自由面速度信号转换为压杆前端面平均压力。首先,基于加汉宁窗短时傅里叶变换处理压杆自由面的速度历程数据,分析各频率成分的到达时间,并与P-C方程的理论结果相对比,识别出杆中弹性波的传输模式;其次,在传输模式分析的基础上,提出了局部相位-幅值联合校正算法,该方法只在符合轴向应力波弥散规律的时频点附近做校正,避开了非弥散的频率成分,传统的频域校正算法主要针对相位校正或相位-幅值联合校正,会校正信号中非弥散频率成分,从而引入附加偏差;最后,开展了多套压杆的验证实验,实验结果表明,压杆01#传播的为一阶轴向弹性应力波,而压杆04#中传播的为前3阶轴向弹性应力波;针对该两压杆信号进行了局部相位-幅值联合校正,获得了校正后的承压面平均应力曲线,与初等理论及全局相位-幅值校正算法给出的结果进行对比,验证了该方法较好地实现了弥散校正和分布不均匀校正。最终研制的近距离冲击波反射压力测试系统量程为3 GPa,分辨率为0.195 MPa,测量不确定度为1.95 MPa。
3 发展建议
针对压杆式冲击波反射压力测试技术的发展,本文提出几点研究建议:
(1)从压杆材料入手,优选出泊松比小、动态强度高及加工工艺好的材料,从根本上减小应力波在杆中的弥散,提高系统频响和量程。
(2)进一步研究新的杆中力学参数测量方法。测点位置靠近杆前端时应力波中各频率成分弥散较小,研究新的传感技术及系统使其靠近前端有利于提高系统频率响应,但须兼顾测量系统的生存问题。
(3)进一步加强杆中应力波传播模式分析及校正方法研究。可预见,今后一段时间内高阶传输模式弥散校正将是研究的重点。
(4)加强压杆式冲击波反射压力测试系统的标准化、系列化、工程化设计,促进该类传感器走出实验室,更广泛地应用于相关领域。

