“华龙一号”堆芯中子学计算的蒙特卡罗源收敛问题
申鹏飞,霍小东,邵 增,杨海峰,张 鹏,王 侃
(1.中国核电工程有限公司,北京,100840;2.清华大学 工程物理系,北京,100084)
蒙特卡罗算法常用于堆芯高精度建模和高保真物理计算中。蒙特卡罗临界计算通常采用源迭代过程,使用用户自定义的源作为初始源,进行输运模拟并将其后代存入中子库中;下一代抽样时,从上一代的中子库中进行随机抽样的方式得到新的源分布,进行输运模拟并重新获得中子库;以此往复,得到收敛源分布后再进行各物理量的统计。
蒙特卡罗的源迭代过程存在源收敛问题,表现为源慢收敛、方差低估计等问题[1-3]。其中,源慢收敛问题体现为从用户自定义的源分布逐步迭代消除初始源分布的高阶项,最终得到本征源分布的过程,在高占优比的模型中耗时较久,甚至需数百非活跃代。而压水堆堆芯模型是典型的高占优比模型,占优比可达0.98~0.99。方差低估计问题体现为在蒙特卡罗活跃代计算中,统计量的计算方差小于真实方差的现象。造成方差低估计现象的原因是蒙特卡罗每个活跃代的统计结果都被视为相互独立。在HOOGENBOOM全堆模型中,组件功率的方差低估计系数(under estimation ratio, UER)可大于90%[4]。综上,在大尺度的高占优比系统中,源收敛问题会显著影响计算资源的分配和计算结果的分析解读,因此需针对各个模型进行蒙特卡罗源收敛问题研究。
“华龙一号”(HPR1000)是我国自主研发的第三代核电技术堆型[5],反应堆采用 177 个燃料组件构成的堆芯(简称“177 堆芯”),具有完全自主知识产权[6],这一新的堆芯设计方案会导致不同的源收敛特性。为深入分析“华龙一号”堆芯蒙特卡罗临界计算的源收敛特性,本文使用keff、香农熵及WD(Wasserstein distance)等判据分析了源慢收敛问题,给出了非活跃代数的建议值,同时计算了栅元、组件和全堆3个层次的集总量和分布量的UER。使用组件功率的实测值与计算值进行了对比,并使用半定量预估消除(semi-quantitative variance underestimation elimination,SeVUE))算法计算了代间相关性影响长度,给出了解决源收敛问题的相关计算参数。计算平台使用国产堆用蒙特卡罗软件RMC。
1 堆芯建模及源收敛诊断
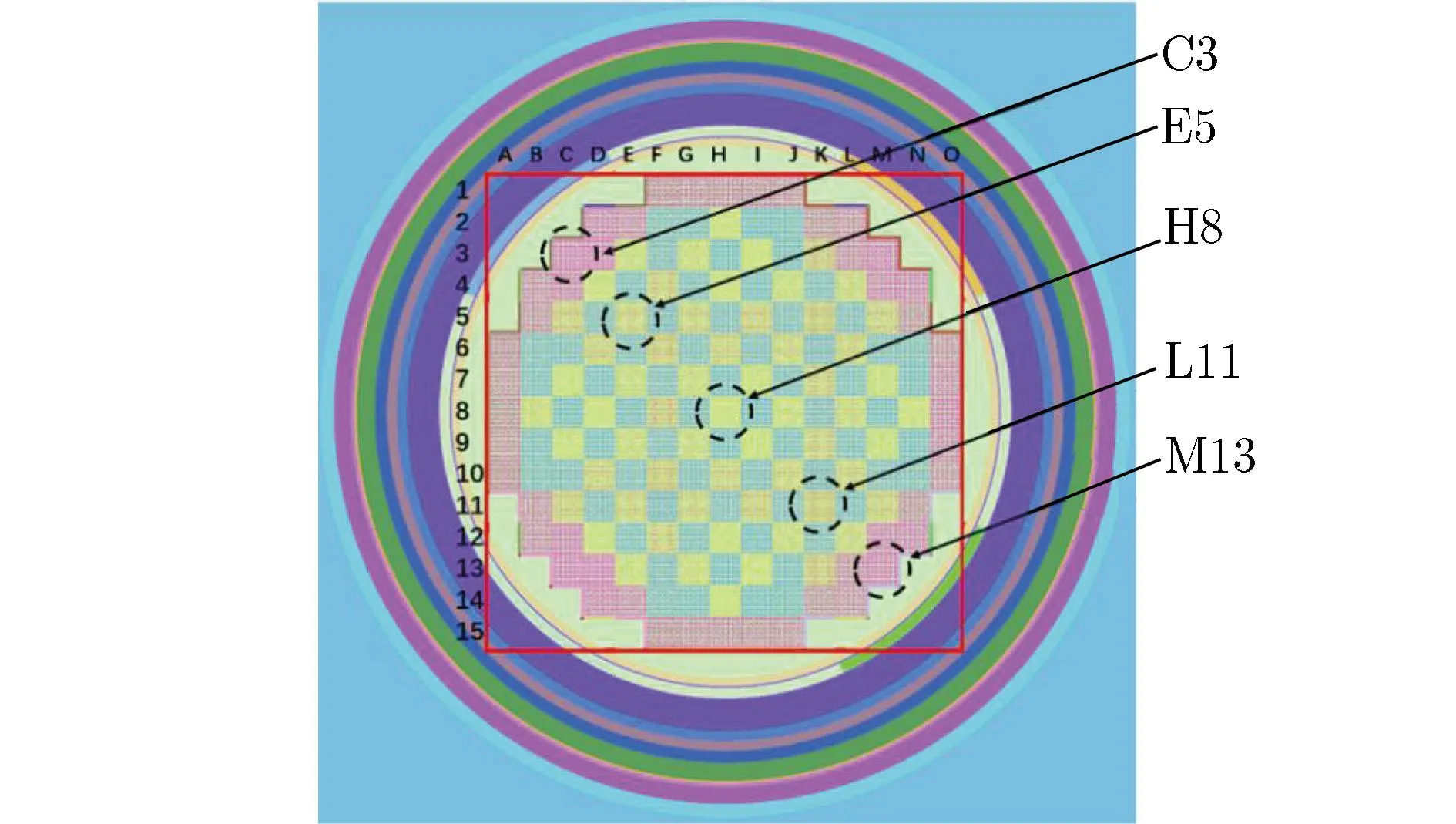
HPR1000堆芯由 177 个先进燃料组件构成。堆芯活性段高度(冷态)为365.8 cm,堆芯高径比为1.13。首循环堆芯燃料组件按235U的富集度分3区装载,富集度分别为1.80%,2.40%,3.10%[6]。“华龙一号”首循环堆芯简化模型如图1所示。
(a)Top view
(b)Side view
为检验源收敛诊断特性,设置不同位置、不同每代粒子数的初始源,并使用keff、香农熵与WD判据进行收敛性分析[7-8]。初始源位置如图1(b)所示,初始源的参数如表1所列。
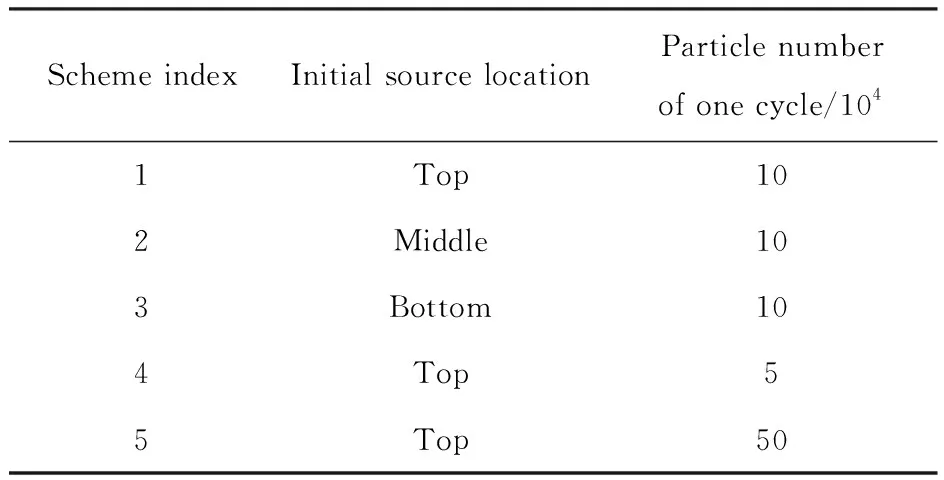
表1 初始源的参数
图2为“华龙一号”堆芯keff随代数的变化关系。由图2可见,数十代内,源实现收敛。香农熵是常用的蒙特卡罗源收敛判据,“华龙一号”堆芯香农熵随代数的变化关系如图3所示。由图3可见,不同初始源设置下收敛特性有所不同:当初始源设置在中部时收敛最快,约100代完成收敛;当初始源设置在顶部、底部时收敛较慢,约200代完成收敛;不同每代粒子数对收敛特性没有影响。

图2 “华龙一号”堆芯keff随代数的变化关系

图3 “华龙一号”堆芯香农熵随代数的变化关系
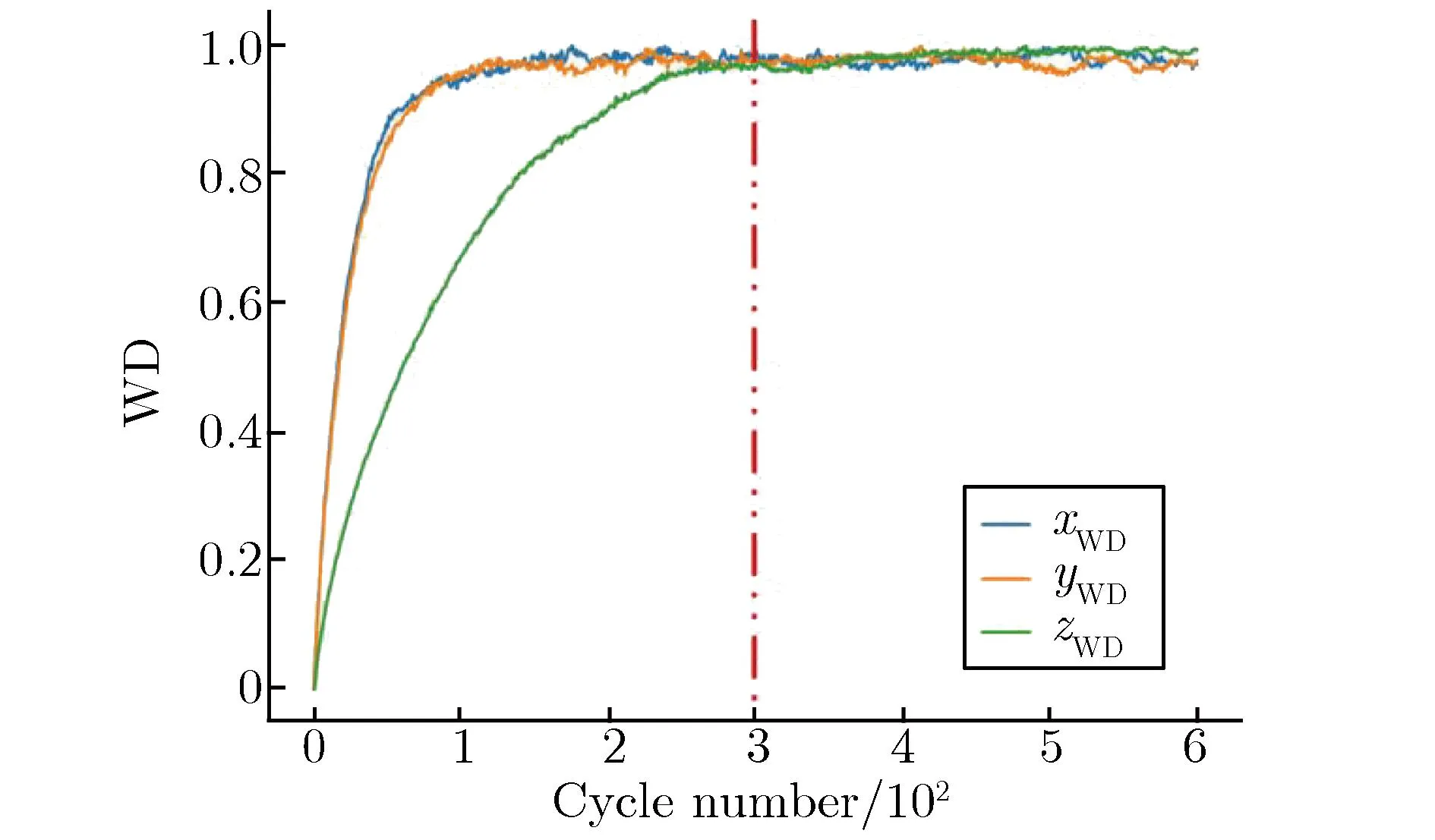
Guo等[8]提出的WD判据是根据裂变源分布的数据特征进行收敛诊断,是一种更保守的收敛判据。该判据分别对3个方向的粒子坐标进行排序并计算其WD(xWD,yWD,zWD),不同初始源设置下堆芯WD随代数的变化关系如图4所示。由图4可见,与香农熵类似,不同初始源设置下收敛特性有所不同:当初始源设置在中部时收敛最快,约200代完成收敛;当初始源设置在顶部、底部时收敛较慢,约300~350代完成收敛。此判据下,还观察到每代粒子数不同时,源收敛特性的差异,当每代粒子数增大时,所需收敛代数略有增加。这是因为每代粒子数增大时,WD距离在收敛后的波动减小,使WD距离收敛到稳态的代数增加。对5种方案的源收敛特性进行综合比较发现,非活跃代参数应设置为大于300代,且keff判据和香农熵判据均存在提前判断收敛的现象。
(a)Scheme index 1(top)

(b)Scheme index 2(middle)

(c)Scheme index 3(bottom)

(d)Scheme index 4(top)
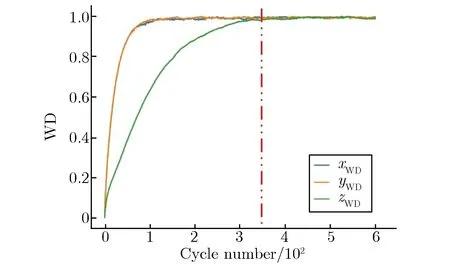
(e)Scheme index 5(top)
2 数值计算方差低估计现象
计算了集总量keff、中子代时间、总功率及组件与栅元功率分布的方差低估计现象。蒙特卡罗临界计算参数如表2所列。参考解及真实方差由40组独立计算得到,其中每次计算设置不同的随机数种子,舍弃单次计算方差σa,使用统计方法得到40组计算值的真实方差σr。方差低估计系数ηUER可定义为
(1)

表2 蒙特卡罗临界计算参数
集总量的方差及方差低估计系数如表3所列。由表3可知,3个参数的方差低估计现象均不明显,方差低估计系数小于±10%以内,与参考解方差的固有波动相近。

表3 集总量的方差及UER
在“华龙一号”的临界分析中,组件及栅元功率等分布量更值得关注。“华龙一号”堆芯组件功率分布的参考解及方差低估计现象如图5所示。由图5(d)可见,组件功率分布的UER为77%~93%,堆芯内部组件的UER相对较低,外侧组件较高。原因是堆芯内部中子自由程有限,外侧组件本代源分布与上代源分布的相关性高于中心区域组件。全部组件的平均UER为89.1%。
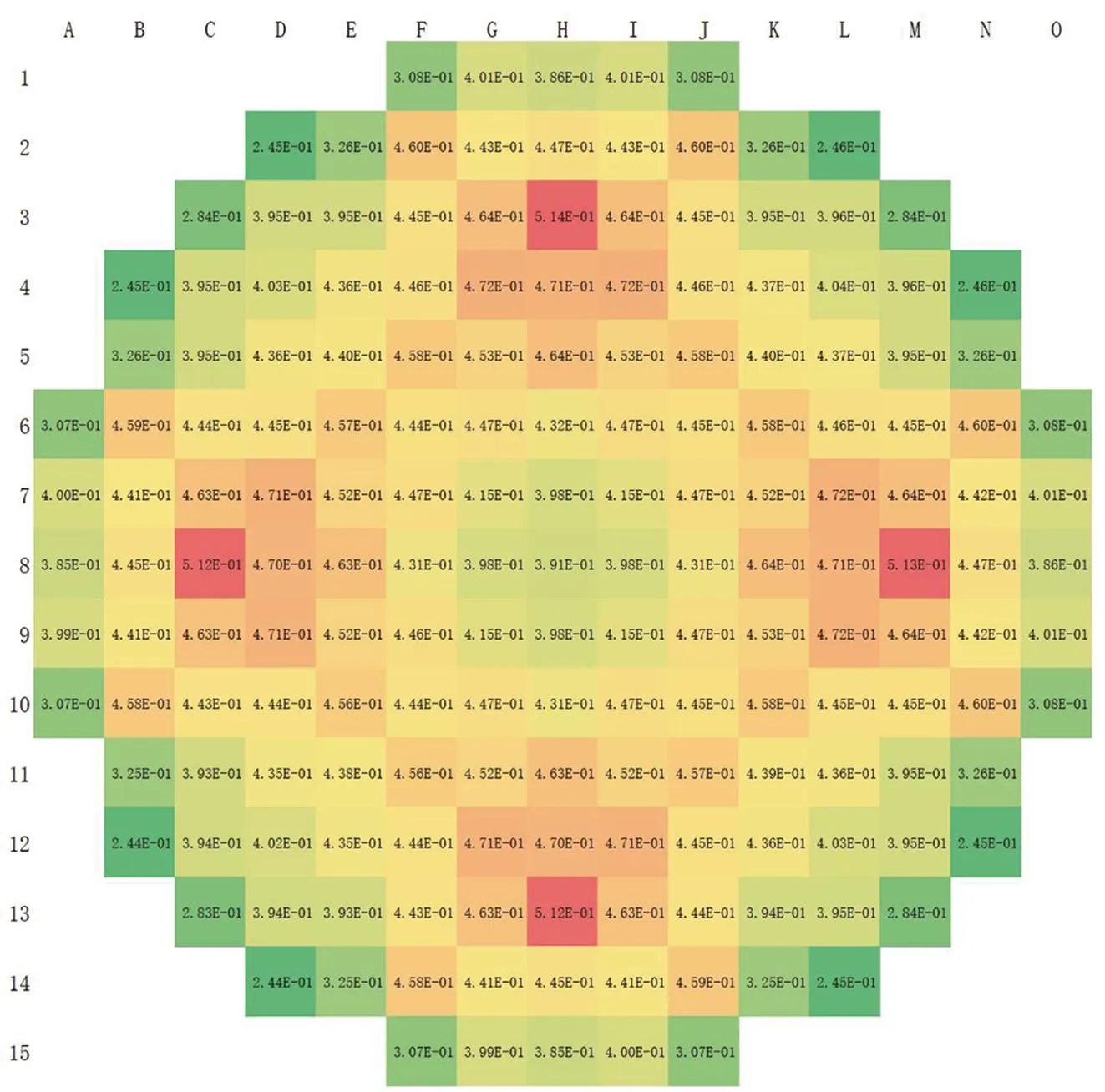
(a)Reference power
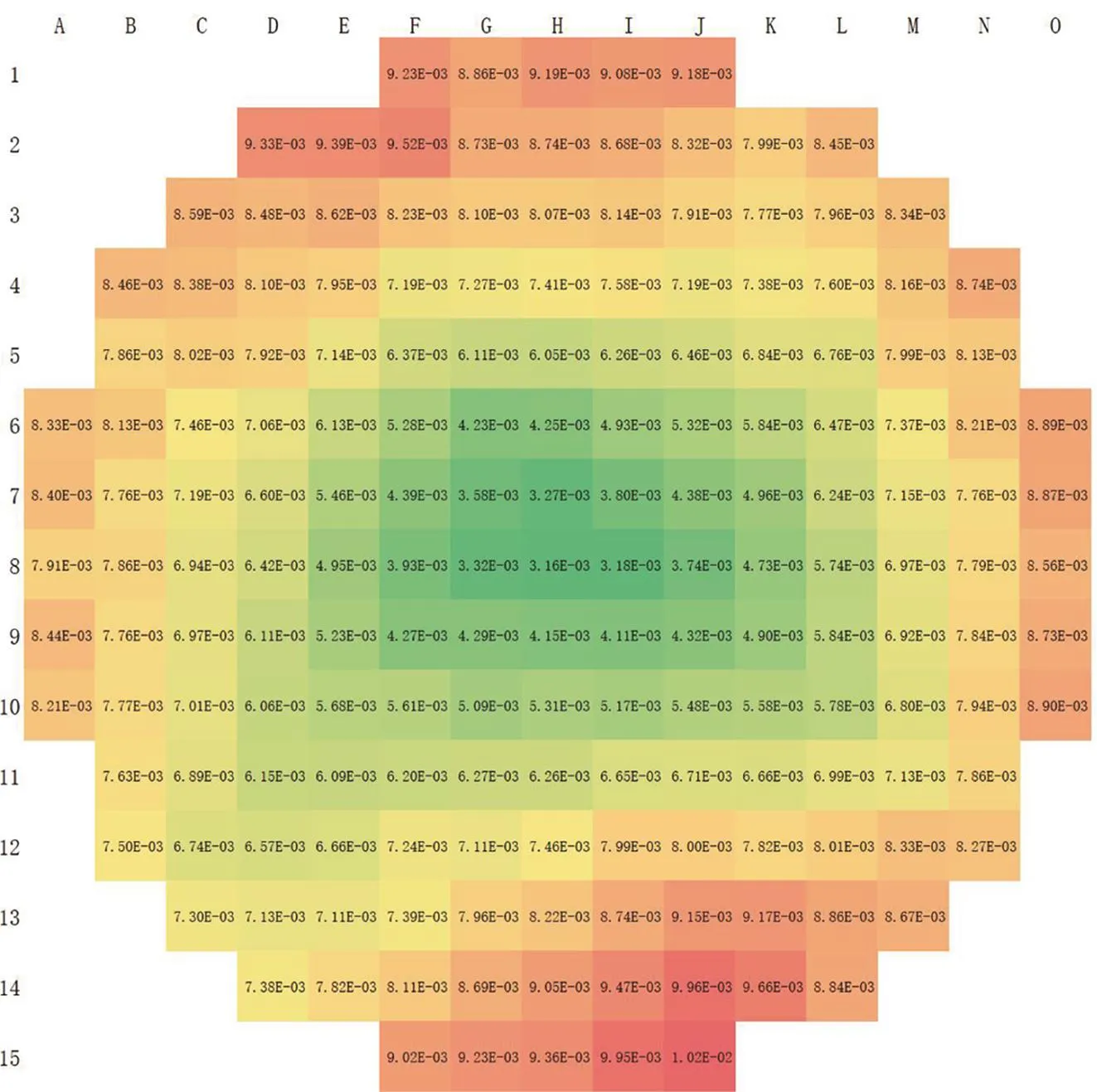
(b)Reference relative deviation
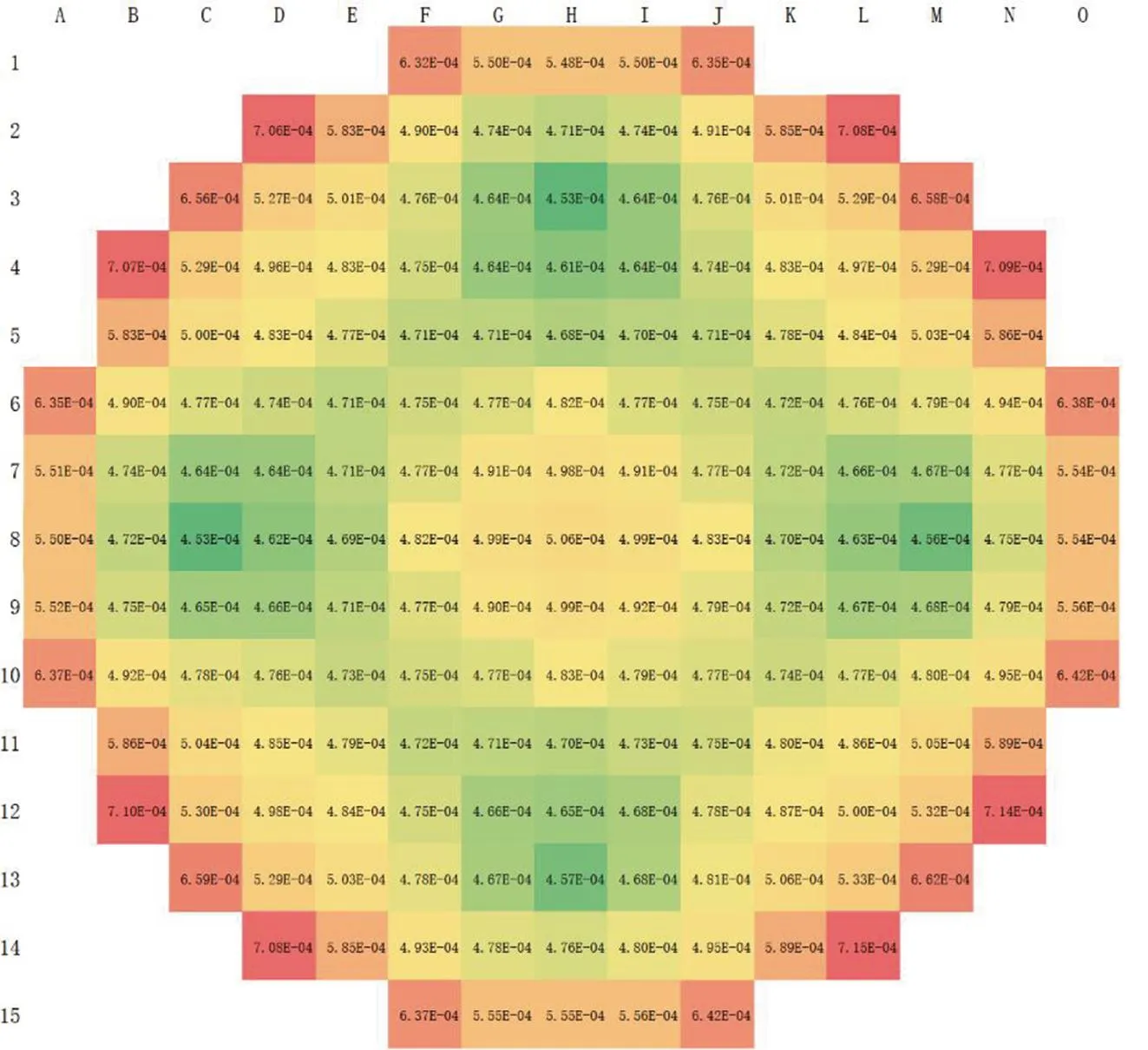
(c)Relative deviation of Monte Carlo single calculation

(d)UER
选取了C3,E5,H8,K11,M13等斜对角分布的5个组件(如图1所示)分析栅元功率分布的方差低估计现象。其中,E5组件的栅元功率分布参考解及方差低估计现象如图6所示。

(a)Reference power

(b)UER
由图6(b)可见,栅元功率分布的UER无明显规律,为23%~53%。5个组件栅元功率分布的平均UER如表4所列。与组件功率分布的方差低估计现象类似,堆芯组件的栅元功率分布的方差低估计现象较不显著,外围组件的栅元功率分布的平均方差低估计系数较高,可达40%以上。

表4 5个组件栅元功率分布的平均UER
因此,功率分布等分布量的方差低估计现象需引起足够关注。在“华龙一号”组件功率分布的计算处理中,应将计算标准差乘以10;在不同位置组件的栅元功率分布计算处理中,通常应将计算标准差乘以1.5。
3 组件实测功率分布对比
将“华龙一号”热态满功率(hot full power, HFP)状态下组件功率的实测值进行比较分析。比较C3,E5,H8组件的实测功率与蒙特卡罗中子学计算的功率差异,并实际观察蒙特卡罗方差低估计现象。各组件蒙特卡罗计算相对偏差如表5所列。
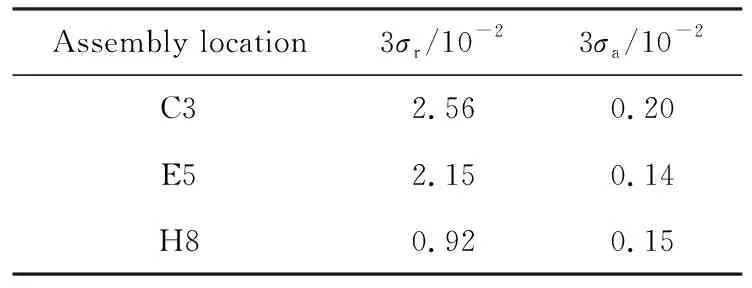
表5 各组件蒙特卡罗计算的相对偏差
C3,E5,H8组件的实测功率与蒙特卡罗40组单次计算功率分布如图7所示。由图7可见,在40组蒙特卡罗独立计算中,单次蒙特卡罗计算得到的组件功率大多数不能在3倍标准偏差内与实测结果吻合。修正了方差低估计现象后,蒙特卡罗计算的参考解与实测功率在3倍真实标准偏差内吻合良好。因此,在实际堆芯的中子学计算中,须采取适当的措施修正方差低估计现象。
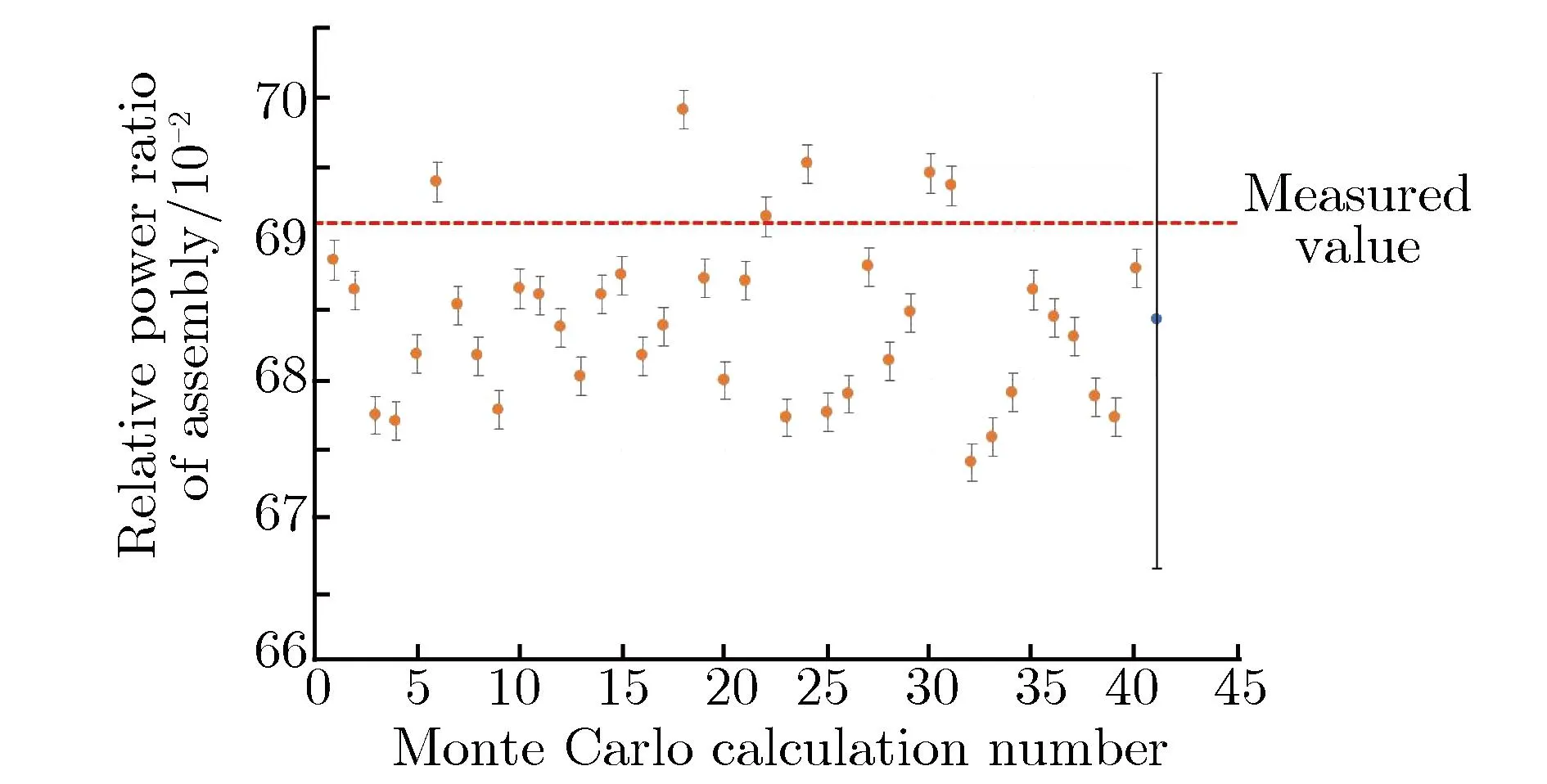
(a)C3

(b)E5
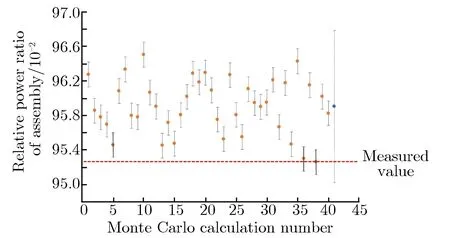
(c)H8
4 代间相关性长度计算
使用SeVUE方法计算“华龙一号”堆芯的代间相关性长度,并消除各个层面的低估计系数[9]。SeVUE方法首先计算蒙特卡罗裂变源分布的平均SWD(Sliced Wasserstein distance)随相隔代数的变化关系,判断出该模型的代间相关性长度,并从理论上证明了模型的代间相关性长度就是组统计方法中的最佳组长度。其中,组统计方法是一种将蒙特卡罗活跃代归并以减弱蒙特卡罗方差低估计的方法,须设置组长度l,将活跃代每隔l代归为多个组,以组为单位统计物理量并计算标准偏差。由于组间裂变源分布的相关性明显弱于代间,因此组统计方法可有效减弱蒙特卡罗方差低估计的现象。但组长度l的设置是一个难点,如l设置过大,组数偏少,统计结果的标准偏差的波动就较大;如l设置过小,组间裂变源分布的相关性就可能较大,从而无法完全消除方差低估计现象。
对于“华龙一号”堆芯模型,其裂变源分布平均SWD随相隔代数的变化关系如图8所示。由图8可见,代间相关性长度为裂变源分布平均SWD达到最大值并开始波动的间隔长度,应为约500代。
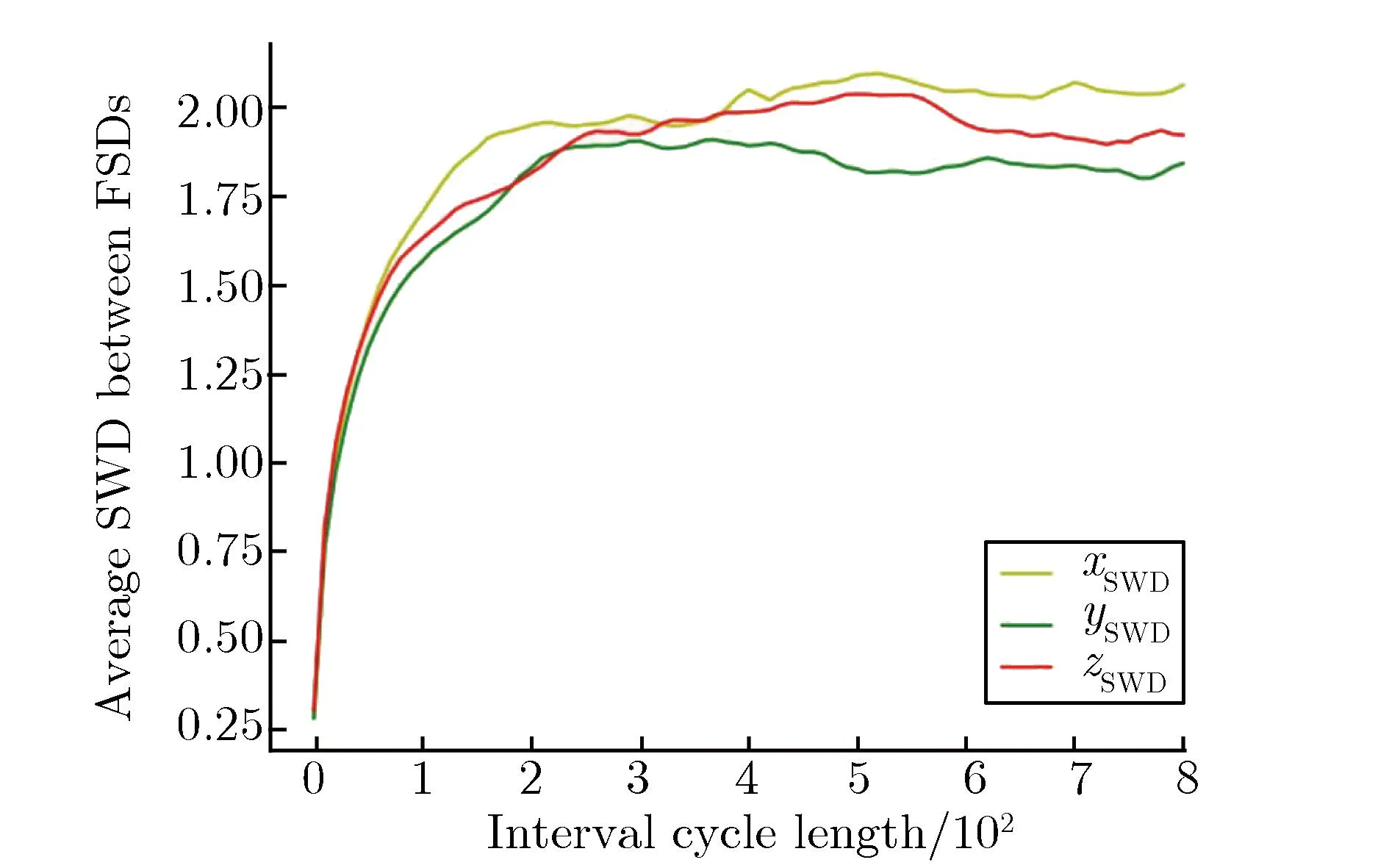
图8 “华龙一号”模型裂变源分布平均SWD随相隔代数的变化关系
SeVUE方法的第二步为蒙特卡罗组统计计算。设置组长度为500代,其他参数与表1相同,得到组件功率分布的UER,如图9所示。由图9可见,使用SeVUE方法消除方差低估计现象后,组件功率分布的UER无明显规律,在-8.9%~14.4%之间波动,平均值为6.3%。

图9 使用SeVUE方法后组件功率的UER分布
栅元功率分布的方差低估计现象被消除。5个组件的栅元平均UER如表6所列。以E5组件为例,其栅元功率分布的UER如图10所示。

表6 使用SeVUE方法后,5个组件栅元功率分布的平均UER
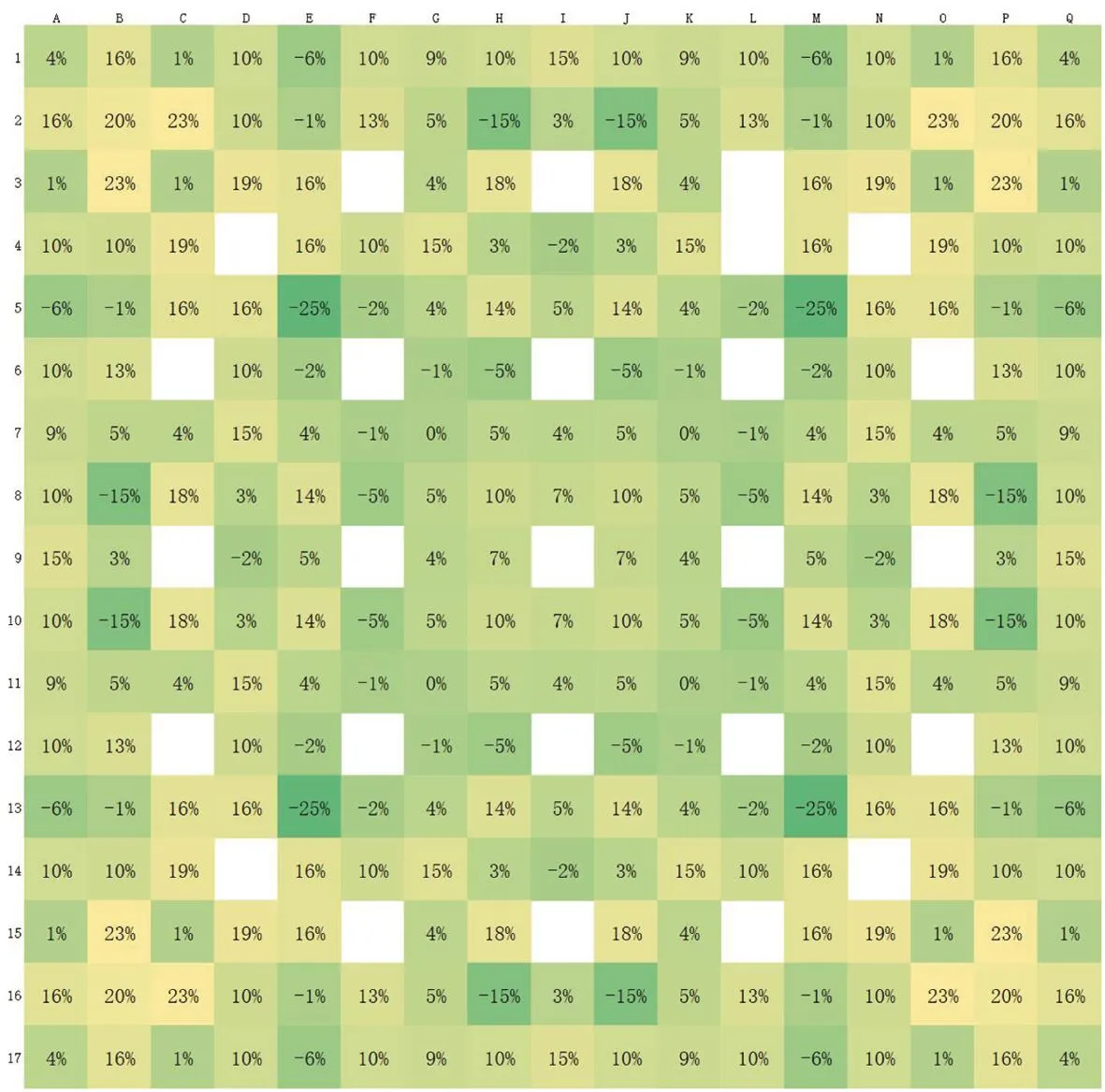
图10 使用SeVUE方法后,E5组件栅元功率分布的UER
由图10可见,栅元功率分布的UER也无明显规律,在-25%~23%之间波动,平均值为6.8%。
因此,除对分布量的计算结果进行系数处理外,可使用组长度为500代的组统计计算,可完全消除临界计算方差低估计现象。
5 结论
本文使用keff分析、香农熵诊断及WD诊断算法分析了“华龙一号”堆芯的蒙特卡罗源慢收敛问题,给出收敛所需的建议非活跃代数为30代。研究了蒙特卡罗方差低估计问题,说明了keff、中子代时间及总功率等集总量的方差低估计现象不显著;对于功率密度分布,进行了栅元和组件两个层次功率分布的UER计算,平均UER分别约为30%和90%,且堆芯外侧的组件功率和栅元功率方差低估计现象较显著。与实测值对比,蒙特卡罗单次计算的组件功率大多数不能在3倍标准差内与实测值吻合;修正了方差低估计后,蒙特卡罗计算的参考解可在3倍真实标准差内与实测值吻合。
本文还使用SeVUE算法计算了“华龙一号”堆芯模型的代间相关性长度,确定约为500代。建议使用系数修正或组长度为500代的组统计法进行“华龙一号”堆芯模型的临界计算分析。

