K波段同轴渡越时间振荡器研究

于 状,巨金川,张 威,周云霄,李 莹,何昌杰,姚宏涛

(国防科技大学前沿交叉学科学院,长沙410073)

K波段是频率范围为18～26 GHz的电磁波,对应的波长范围为11.54～16.67 mm,具有增益高、相对频带宽等特点[1],应用十分广泛。然而,现阶段关于K波段的高功率微波源鲜有公开报道,因此开展K波段高功率微波源的研究具有重要意义。

渡越时间振荡器(transit-time oscillator, TTO)具有结构简单、工作稳定及模式单一等特点,已成为一种重要的高功率微波产生器件[2]。然而关于高功率输出TTO的相关研究大多集中在C、X等波段[3-5],在Ku及以上高频段的器件输出功率相对较低,主要原因是高频段器件尺寸较小,器件的功率容量有限。在前期的Ku波段TTO仿真中,采用同轴结构的单级三间隙调制腔与三间隙集中式能量提取腔,实现了1 GW的微波输出功率,电子束调制深度为123.5%,束波功率转换效率为30%,器件过模比为4.1[6];在Ka波段TTO仿真中,采用同轴结构的单级四间隙调制腔与三间隙集中式能量提取腔,实现了1.27 GW的微波输出功率,电子束调制深度为121%,束波功率转换效率达38.5%,器件过模比约为8.9[7]。采用大过模比、同轴结构多间隙调制腔与多间隙提取腔是增大高频段器件功率容量的一种常用方式。而所述Ku与Ka波段的高频段器件结构存在电子束电流进一步增大,对电子束的调制能力不足的问题,不能进一步满足提高输出功率的需求。

如何提高电子束调制深度、增大器件功率容量成为高频段器件实现更高输出功率研究的重点。本文采用大过模比同轴结构,设计了一种两级多间隙调制腔与多间隙分布式能量提取结构的K波段高功率渡越时间振荡器。在电子束中心半径为45.5 mm(过模比约为5.7)的条件下,对器件进行了模拟仿真,结果表明,该器件能够输出的微波功率为2.2 GW,束波功率转换效率达44%,输出微波频率为18.55 GHz,且频谱纯净。

1 器件高频结构设计

图1为本文设计的TTO结构示意图。由图1可见,TTO主要由二极管、反射器、第一级调制腔、第二级调制腔及双通道分布式提取腔等结构组成。其中,反射器的作用是隔离漂移通道中的横电磁波(transverse electromagnetic wave, TEM),避免其反向泄漏到二极管区域,干扰电子束的正常发射与传输[8]。TTO器件工作过程如下：二极管产生的电子束经过两级调制腔的速度调制后,在漂移段中进行密度调制,在此过程中基波电流不断增大,最终电子束到达提取腔位置,此时基波电流达到最大值,随后电子束中的交流功率转换成微波功率通过两个同轴波导输出。

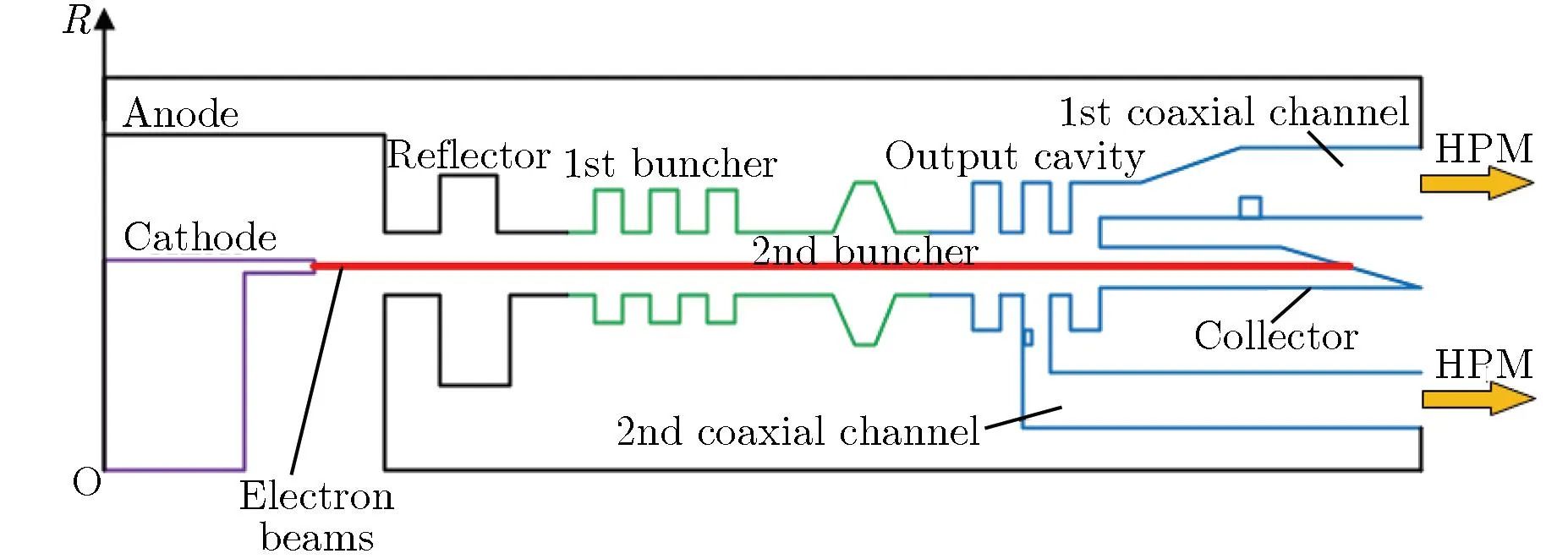
图1 本文设计的TTO结构示意图

1.1 两级调制结构

调制腔的作用是对电子束进行初步调制,是TTO实现高基波电流调制深度的关键结构。调制腔的间隙数目、耦合系数及级数等参数都对电子束调制深度有重要影响。这些影响都可通过腔中电场模式分布与外观品质因数Qe等参数进行表征。其中,Qe表示腔体耦合输出微波功率的能力。研究表明,调制腔间隙数目越多,基波电流调制深度越高,最终实现的功率转换效率也越大;然而腔体间隙数目过多,又会导致腔中模式隔离度减小,容易引入非工作模式而影响器件的正常工作,因此腔体数目一般采用三间隙。但三间隙调制腔对电子束的调制能力不足,为实现K波段2 GW的微波输出功率,需增加第二级调制腔。由于电子束到达第二级调制腔时已携带了较强的谐波信号,在第二级调制腔中会激励起频率相近的本征场,为减少被激励的非工作模式数目[9]并增大腔体的功率容量,第二级调制腔采用单间隙梯形结构[10]。最终确定的两级调制腔由三间隙矩形腔与单间隙梯形腔级联的方式构成,图2为两级调制腔级联结构示意图。

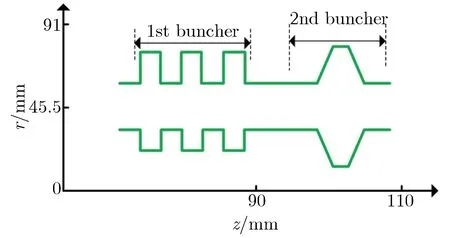
图2 两级调制腔级联结构示意图

采用电子负载电导理论[11]计算得到第一级三间隙调制腔中不同纵模对应的归一化电子电导G/G0随传播常数β的变化关系如图3所示。由图3可见,传播常数β为0.39～0.53时,只有TM012模式可被激励起来,因此选择TM012模作为腔体工作模式。

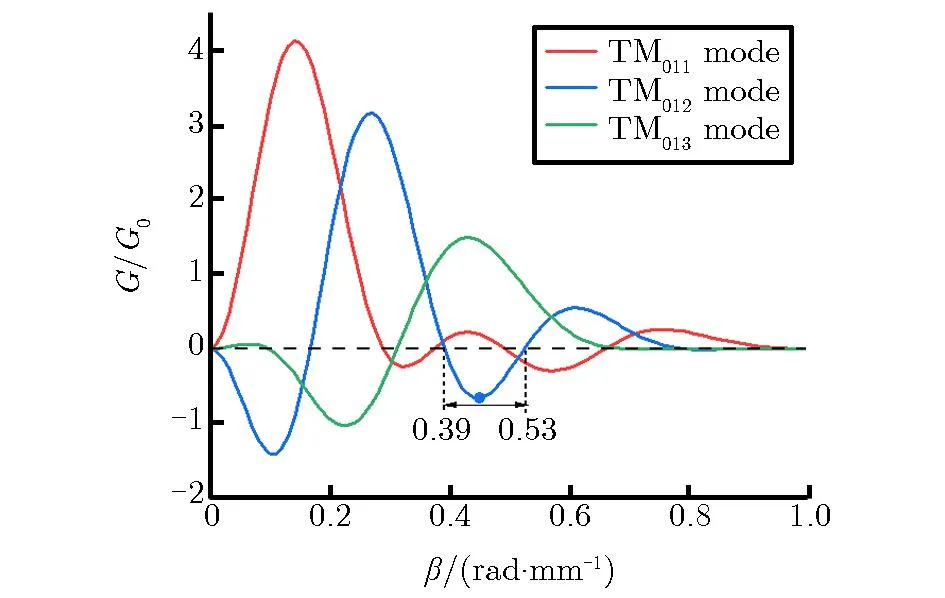
图3 第一级调制腔中不同纵模对应的归一化电子电导随传播常数的变化关系

此外,传播常数β与二极管的工作电压V的关系可表示为

(1)

其中：f为腔体工作频率(本文调制腔工作频率为18.6 GHz);c为光速。当β为0.45时,TM012模式的归一化电子电导绝对值最大,此时对应的二极管电压为500 kV,因此选500 kV作为器件的工作电压。

与速调管放大器不同,TTO中腔体之间有耦合,加载第二级调制腔后必然会影响到第一级调制腔对电子束的调制,所以两级腔体的Qe值选择必须适当。第一级调制腔基波电流I随Qe的变化关系如图4所示。由图4可见,当Qe<588时,随Qe值的增大,基波电流调制能力不断增强,即图中的区域I;当Qe值继续增大时,腔体泄漏能量减小,对腔中电场的影响变小,电流调制能力达到饱和,基波电流稳定在11.3 kA附近,即图中区域II。设基波电流最大处与第一级调制腔的第三间隙最右端之间的距离为D(即电子束漂移距离),由于要级联第二级调制腔,为了不影响后续腔体的加载,D值不能太小。

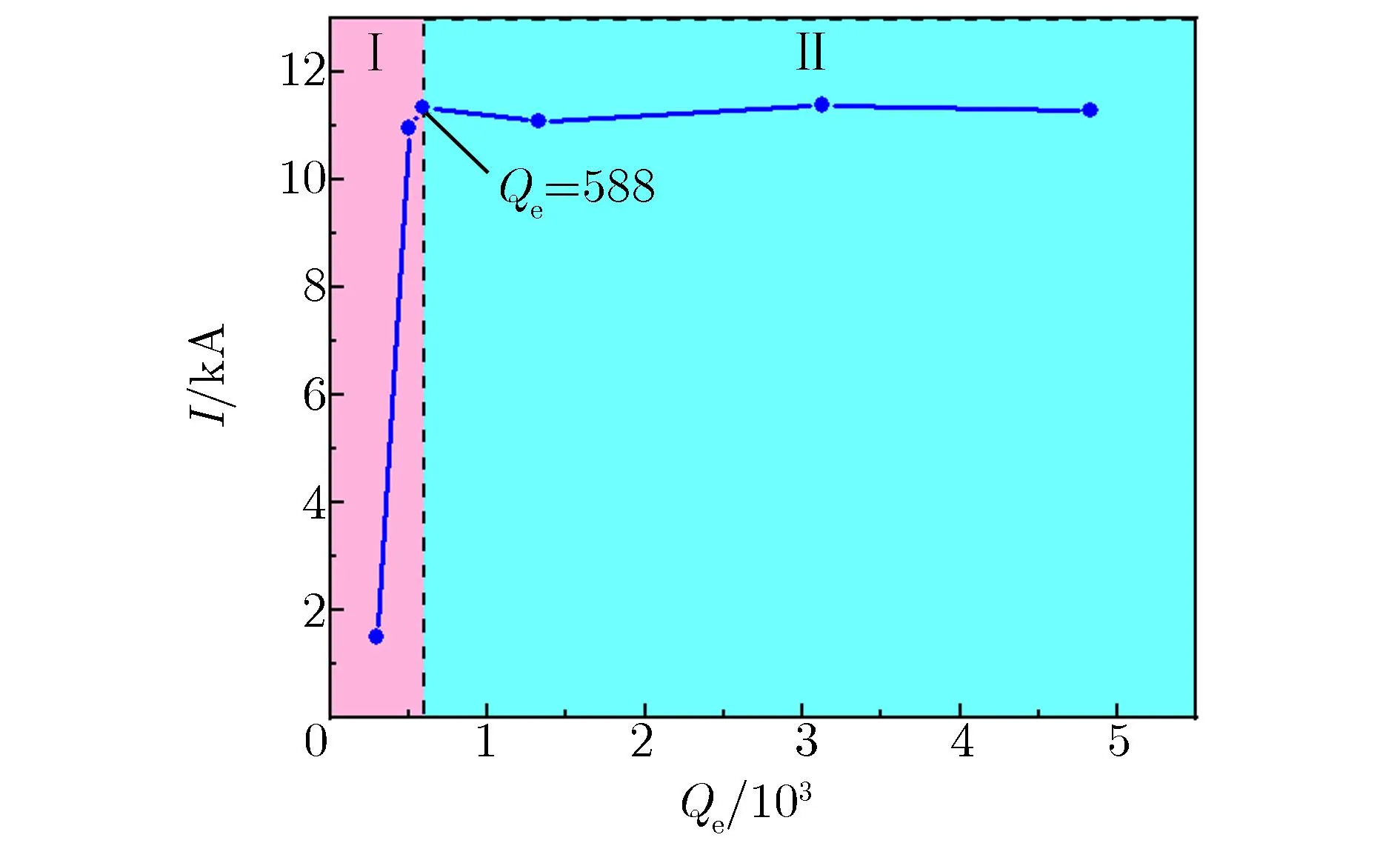
图4 第一级调制腔基波电流随Qe值的变化关系

第一级调制腔基波电流I、距离D及腔体谐振频率f随Qe值的变化关系如图5所示。由图5可见,随Qe值的增大,距离D逐渐减小,这是因为Qe值增大,腔体调制能力增强,在实现相同基波电流调制深度时,电子束漂移距离变短。而谐振频率f主要与腔体径向尺寸有关,随Qe值的变化不明显。

综合图4与图5的结果,第一级调制腔应选择基波电流调制深度比较高、电子束漂移距离较长的结构,即应选用高Qe值腔体,经过仿真优化后选择腔体的Qe为3 125。

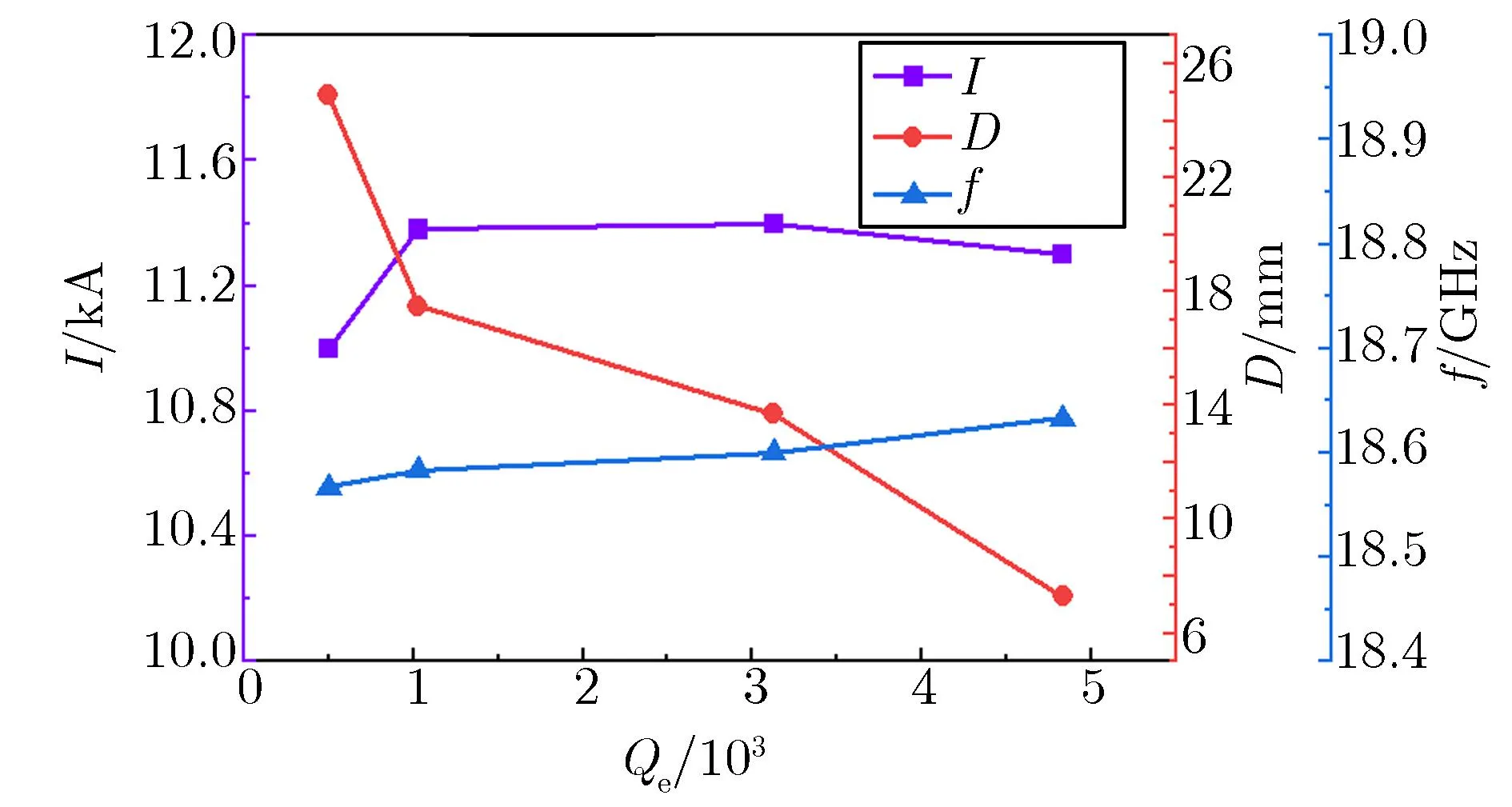
图5 第一级调制腔基波电流I、距离D及腔体谐振频率f随Qe的变化关系

经高度调制的电子束到达第二级调制腔时已携带了大量的交流分量,因此在第二级调制腔处小信号理论已不再适用。第二级调制腔只起到电流放大作用,电流的频率由第一级调制腔牵引。在第一级调制腔Qe为3 125的条件下,对第二级调制腔进行测试。图6为基波电流与腔中微波场饱和时间随第二级调制腔Qe的变化关系。由图6可见,随Qe的增大,基波电流急剧减小,这是因为Qe太大时腔体对电子束调制能力较强,而经过第一级调制的电子束已携带大量能量,再经第二级调制腔深度调制后出现了过调制现象,电子束去群聚使基波电流反而减小;同时,由于Qe太大,导致腔体中电场填充时间太长,造成腔体中电场饱和时间明显增加。图7为电子束离开第二级调制腔后获得最佳群聚时,电子束漂移距离D随Qe值的变化关系。由图7可见,随Qe的增加,最佳漂移距离D逐渐减小,尤其是当Qe>2 000时,D接近2 mm,这已影响了后续提取腔的加载。综合图6与图7的结果,确定第二级调制腔应采用较小的Qe值,经过仿真优化后选择采用腔体的Qe为296。

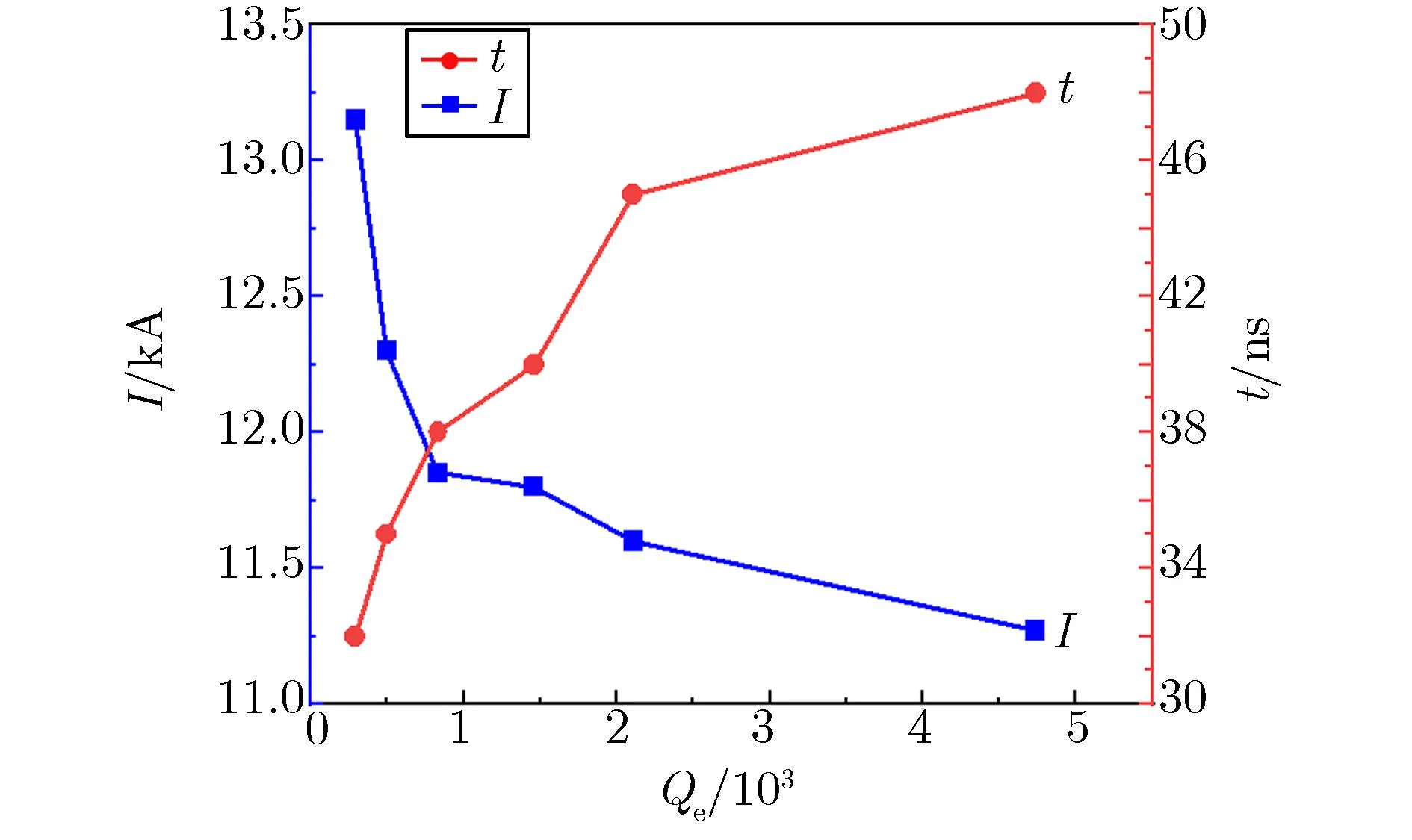
图6 第二级调制腔基波电流I与电场饱和时间t随Qe值的变化关系

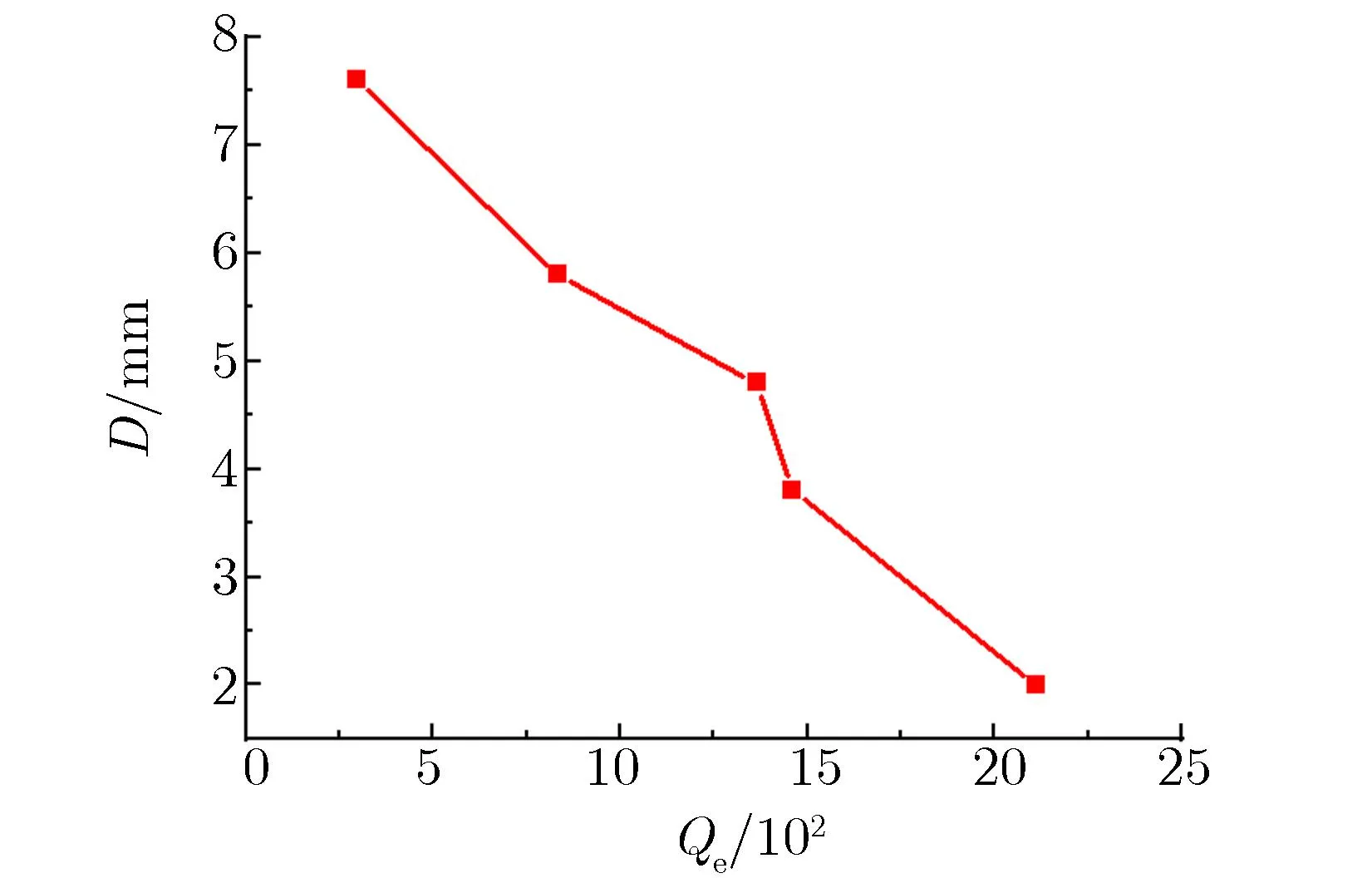
图7 电子束离开第二级调制腔后获得最佳群聚时,电子束漂移距离D随Qe值的变化关系

在二极管电压为500 kV,电流为10 kA,外加导引磁场磁感应强度为0.78 T的条件下,对上述选用的两级调制腔进行测试,有无第二级调制腔时,基波电流随轴向位置的变化关系如图8所示。由图8可见,与无第二级调制腔相比,级联第二级调制腔后,基波电流由原来的11.4 kA增加到13.1 kA,调制深度提高了17%,总调制深度达到131%,为器件高效率输出奠定了基础。

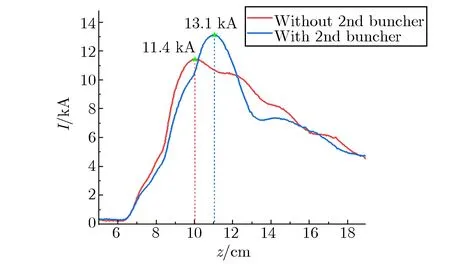
图8 有无第二级调制腔时基波电流随轴向位置的变化关系

1.2 双通道分布式能量提取结构

从电子束中提取交流功率转化成微波功率的能力及腔体表面最大电场强度是提取腔的两个关键参数[12]。集中式与分布式能量提取结构如图9所示。图9(a)为TTO中常见的集中式能量提取结构,即所有能量在提取腔最后一个间隙通过耦合口输出。随着器件工作频率的提高与输出功率的增大,对提取腔的功率容量要求也越高,研究表明,通过增加提取腔间隙数可降低腔体表面最大电场强度[13],但产生非工作模式的可能性也越大,所以必须改变提取腔结构来增大功率容量。研究表明,三间隙提取腔中最大电场强度常出现在第二间隙下端,因此考虑在提取腔第三间隙输出的基础上,在第二间隙开口,构成如图9(b)所示的双通道分布式能量提取结构[14],可进一步通过通道合成的方式实现两个通道输出功率的叠加[15]。

当两种结构左端均注入1 W的功率时,由图9可见,集中式与分布式能量提取结构最大电场强度分别为0.31,0.17 kV·cm-1,与集中式能量提取结构相比,分布式能量提取结构最大电场强度降低了45.16%,功率容量约为前者的3.3倍,有利于在K波段高功率输出。

(a)Centralized energy extraction structure

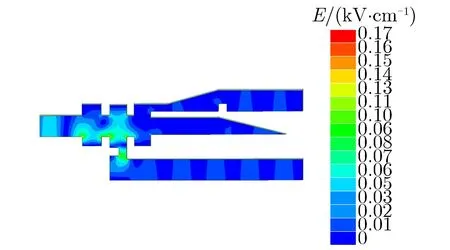
(b)Distributed energy extraction structure

对图9所示的两种能量提取结构进行粒子模拟,得到的两种能量提取结构最大轴向电场强度分布如图10所示。由图10可见：当输出功率Pout为1.2 GW时,集中式能量提取结构最大轴向电场强度为1.51 MV·cm-1;当输出功率Pout为2.0 GW时,分布式能量提取结构最大轴向电场强度为1.45 MV·cm-1。由此可得,采用分布式能量提取结构可在实现更高输出功率的同时,具有更低的电场强度,说明采用该结构的器件具有更大的功率容量。

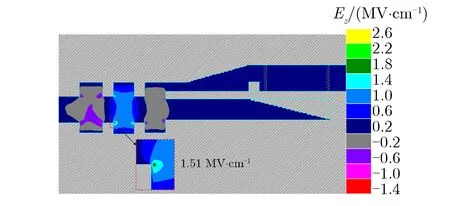
(a)Centralized energy extraction structure when Pout=1.2 GW

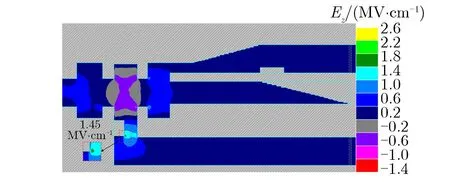
(b)Distributed energy extraction structure when Pout=2.0 GW

通道保持第1.1节所述调制腔结构不变,器件双通道总输出功率Pout及分布式能量提取腔间隙电压Vg随Qe的变化关系如图11所示。由图11可见：当Qe>40时,随着Qe的增加,腔体储能能力增强,微波耦合输出减少,导致输出功率减小;当Qe=40时,腔体总输出功率达到最大值2.2 GW;当Qe<40时,随着Qe的减小,腔体能量损耗增加,三个间隙电压急剧减小,与电子束之间的互作用程度减弱,导致输出功率降低,尤其是当Qe=33时,三个间隙电压中,最大的第二间隙电压小于275 kV,束波互作用程度较低,使输出功率较低。综合以上分析,选定分布式能量提取腔体Qe值为40。

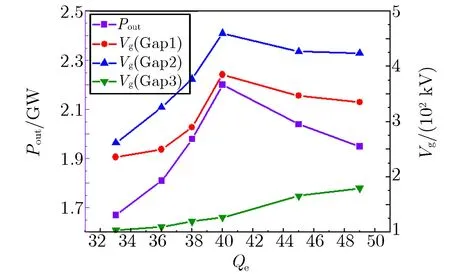
图11 双通道总输出功率Pout,间隙电压Vg随Qe值的变化关系

2 粒子模拟

在二极管电压为500 kV,电流为10 kA,外加导引磁场磁感应强度为0.74 T的条件下,对图1所示TTO整管结构进行粒子模拟。其中,双通道分布式能量提取结构第一与第二同轴输出波导的平均输出功率P随时间t的变化关系如图12所示。

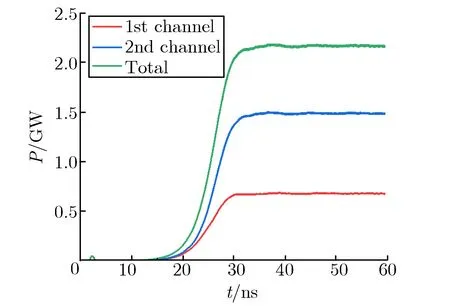
图12 双通道分布式能量提取结构的平均输出功率随时间的变化关系

由图12可见,第一与第二同轴输出波导输出的微波功率分别为0.69,1.51 GW,总输出功率为2.2 GW,相应的束波功率转换效率达44%。然而考虑到两个输出端口中的微波相位差,总输出功率不能简单地代数相加,后续工作会采用文献[15]中的方式设计合路器与相位调节波导,通过相位调节波导对双通道输出微波的相位进行调整,确保在合路器入口处,双端口输出微波相位一致,从而实现两路微波的高效率合成。

双通道分布式能量提取结构输出微波频率如图13所示。由图13可见,双通道输出频率均为18.55 GHz,倍频分量极小,无杂频,频谱纯净。双通道分布式能量提取结构中电子束功率随轴向位置变化关系如图14所示。由图14可见,电子束在提取腔第一与第二间隙损失的功率分别为1.10,1.01 GW,二者之和占总输出功率的95.9%,这是因为前两个间隙电压远远大于第三间隙电压,电子束经过前两个间隙时已经失去了绝大部分能量。

图13 双通道分布式能量提取结构输出微波频率

图14 双通道分布式能量提取结构电子束功率随轴向位置变化关系

磁场磁感应强度为0.3～0.82 T时,TTO器件输出微波的功率Pout和频率fout随磁场磁感应强度B的变化关系如图15所示。由图15可见：当磁场较小时,由于对电子束约束能力不足,导致电子束径向发散较大,束波互作用降低使输出功率较低;随着磁感应强度的增加,电子束径向发散减小,轴向传输稳定使束波互作用增强,输出功率提高;当B为0.46 T时,器件输出功率为1.984 GW,功率转换效率达到39.7%,当B为0.46～0.82 T时,器件输出功率均大于1.94 GW,相应的功率转换效率大于38.8%,表明器件在较低的磁感应强度下可正常工作,具有永磁封装的潜力;输出微波频率则随磁感应强度变化不明显。

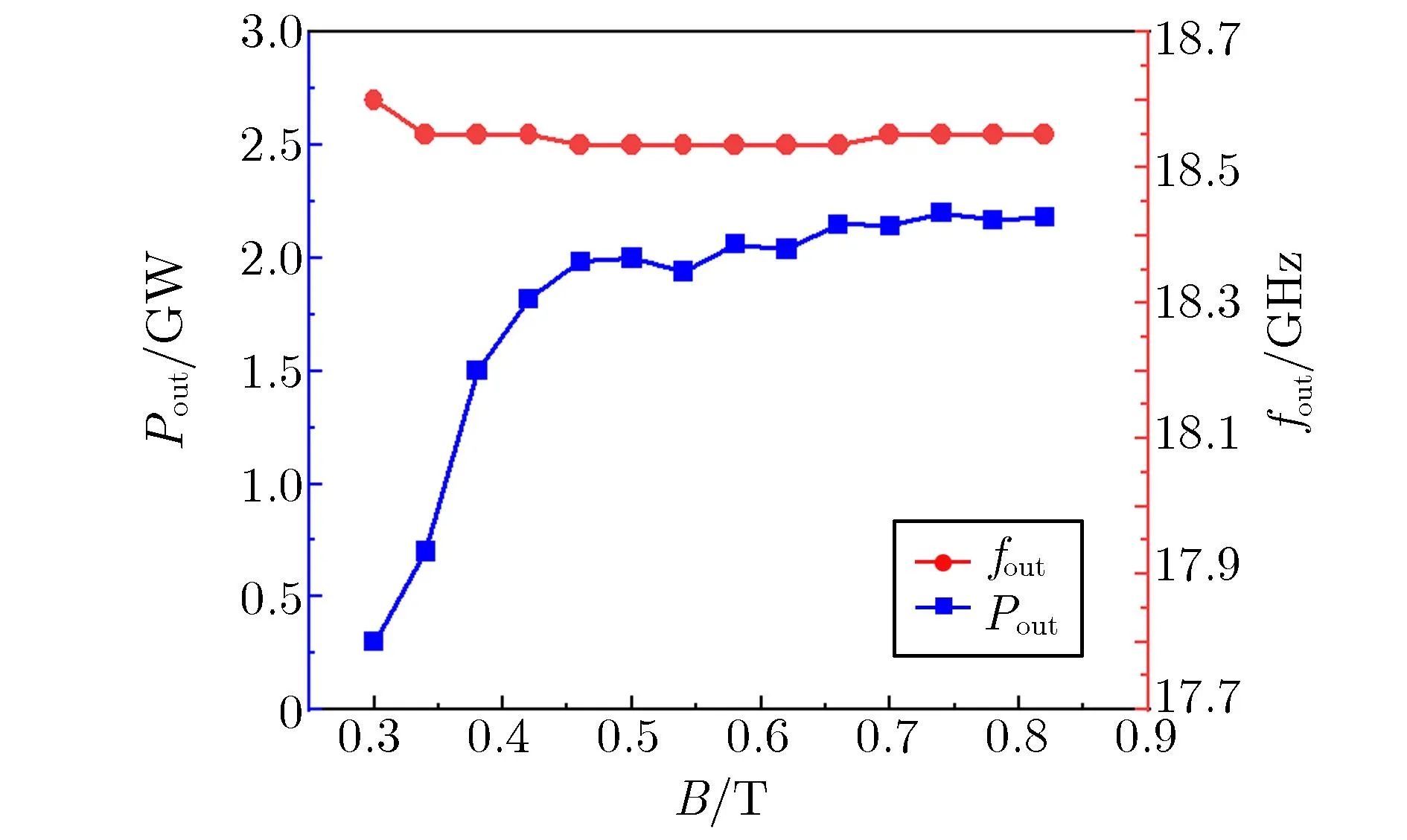
图15 TTO器件输出微波的功率Pout和频率fout随磁场磁感应强度B的变化关系

3 结论

本文采用粒子模拟方法对K波段同轴渡越时间振荡器进行了研究,通过两级调制结构提高了电子束调制深度,通过双通道分布式能量提取结构增大了提取腔的功率容量。经粒子模拟软件对器件的优化,在二极管电压为500 kV,电流为10 kA,外加导引磁场磁感应强度为0.74 T的条件下,输出微波功率为2.2 GW,输出微波频率为18.55 GHz且频谱纯净,束波功率转换效率达44%。在磁感应强度为0.46 T的条件下,器件可实现输出功率大于1.98 GW,功率转换效率大于39.6%,具有低磁场条件下运行的潜力。后续计划开展相应的实验研究。