挖掘定点，优化解题*

刘晓静 戚有建

江苏省扬州教育科学研究院 (225007) 江苏省扬州中学 (225009)

在研究与动直线有关的问题时，有些动直线恒过定点，解题时若能抓住这“点”，从定点入手，把定点作为寻找解题思路的切入点和突破口，往往可以另辟蹊径，起到事半功倍的效果.下面结合几道例题，介绍动直线恒过定点在解题中的应用.

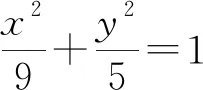
分析：通法是将直线和椭圆方程联列，然后用两点间距离公式或弦长公式处理.另外，本题也可以从动直线恒过定点入手，出奇制胜，轻松解决.

例2 点P(2,1)到动直线l:(m+3)x+(1-2m)y+6-5m=0的距离的最大值为.

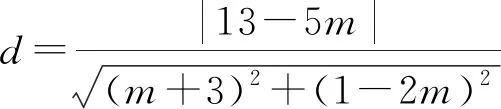
例3 过原点O作直线l:ax+by=a的垂线，垂足为P，则动点P围成的图形面积为.

分析：通法是设垂线OP方程，联列方程求出垂足P点坐标，然后研究P点轨迹.若从动直线恒过定点入手，可减少运算量.

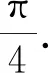
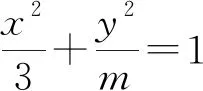
分析：通法是将直线和椭圆方程联列，然后从方程的角度来研究，即将恒有公共点转化为方程恒有解.若从动直线恒过定点入手，可回避联列方程减少运算量.

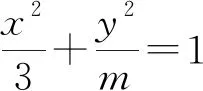
分析：先证明直线MN过定点，此时动点D就在圆上运动.

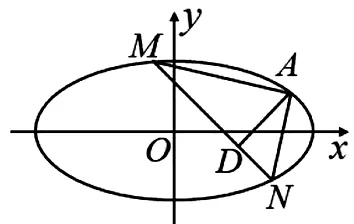
图1

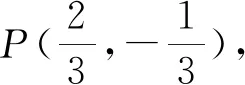
分析：先证明直线PQ过定点，然后构建关于S△BPQ-S△APQ的目标函数求最值.

图2

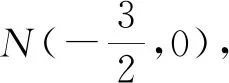
从以上几道例题可以看出，解题时若能充分利用动直线过定点这一已知条件，或者挖掘出动直线过定点这一隐含条件，往往能抓住问题本质，从而优化解题思路、简化解题过程，提高解题效率.