圆锥曲线的定义在解题中的运用

方志平

广东省惠州市第一中学 (516007)

定义是揭示事物本质属性的思想形式，面对一个数学对象，回顾它的定义，常常是解决问题的锐利武器.圆锥曲线的定义是分析、研究、解决圆锥曲线问题的重要依据与手段,是圆锥曲线几何性质、定理的“ 起源”.圆锥曲线的很多问题都与定义紧密相连，圆锥曲线的定义渗透在圆锥曲线的各个方面.因此合理应用定义是寻求解题捷径的一种重要方法.本文将借用圆锥曲线的定义巧解一些数学试题，希望能给大家一点启发.

1.巧用椭圆的定义求解

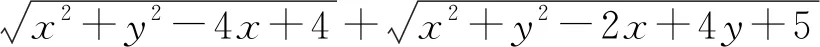
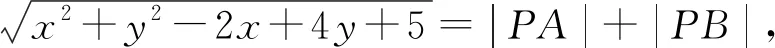
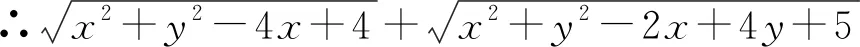
评注：本题通过椭圆的定义，把到右焦点的距离和到左焦点的距离进行相互转化，再利用数形结合的思想，使问题巧妙获解.

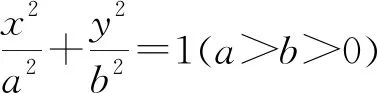
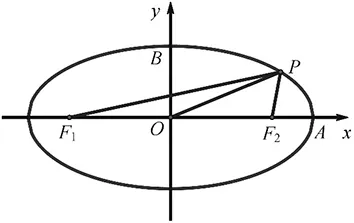
图1

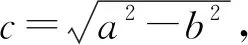
评注：本题求解过程中两次用到椭圆的定义，充分揭示了椭圆的本质特征，椭圆上无论是已知点，还是未知点都具有椭圆的几何意义，即到两个焦点距离的和是定值.

2.巧用双曲线的定义求解

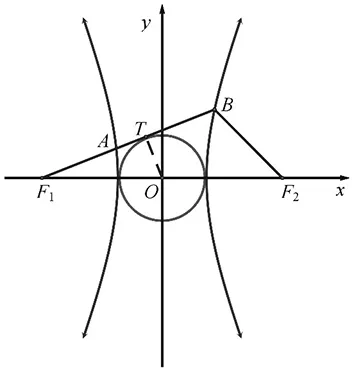
图2

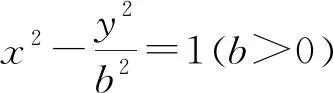
微信的自定义菜单是微信与用户进行一对一交流的重要渠道。菜单功能是与本馆读者建立紧密联系的重要渠道，积极开发菜单功能能够增加用户黏度，不断壮大粉丝群体。如开发个人中心菜单，让学生在微信菜单下绑定读者证信息，能够在微信终端自助进行图书续借，查找本馆的馆藏资源，让用户随时随地了解馆藏信息，不用亲自来到图书馆，也能实现便捷自助服务。

评注：本题在求解过程中，巧妙运用双曲线的定义，并注意挖掘题目隐含的几何意义，避免烦琐的推理与运算，从而快速、准确地解决了问题.

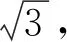
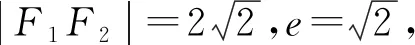
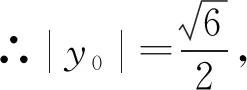
∴∠F1PF2=60°.

评注：为了求∠F1PF2,联想到在△PF1F2中用余弦定理，但|PF1|和|PF2|长度未知,考虑|PF1|和|PF2|又是双曲线的两个焦半径，根据题意，于是想到利用双曲线的第二定义求解.

3.巧用抛物线的定义求解

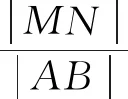
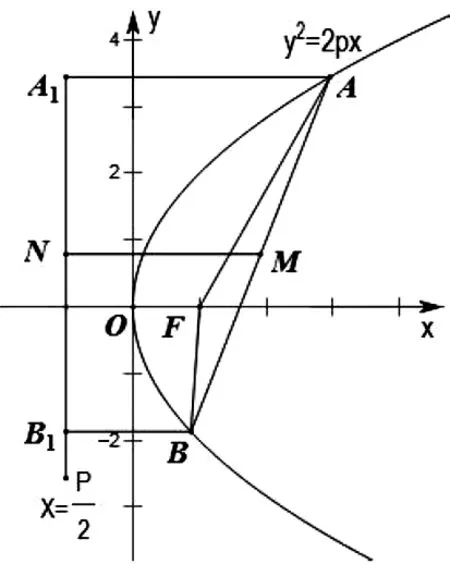
图3

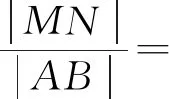
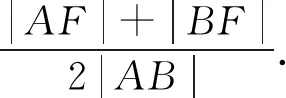
评注：巧用抛物线的定义，将抛物线上的点到其焦点的距离和到准线距离进行互化，是解决本题的重要策略.在△ABF中，利用余弦定理，再结合基本不等式问题顺利得到解决.

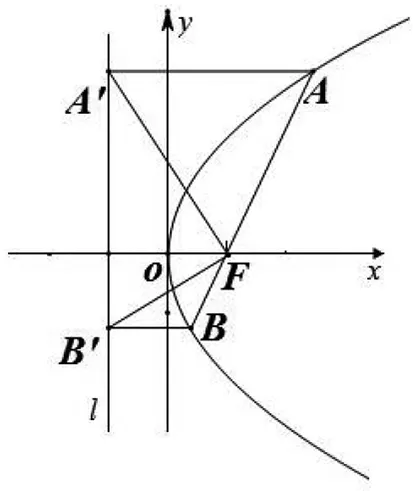
图4

例6 如图4,已知抛物线y2=2px(p>0)的焦点为F,准线为l,过点F的直线与抛物线交于A、B两点,且|AB|=3p.设点A、B在l上的射影分别为A′、B′，今向四边形AA′B′B内任投一点M，则点M落在△FA′B′内的概率是.

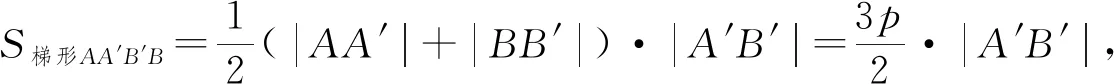
评注：由于AB是过焦点的弦，且弦长已知，此弦长可拆分为两个焦半径|AF|,|BF|的和，于是联想到抛物线的定义，从而求得|AA′|+|BB′|=|AF|+|BF|=|AB|=3p,至此，问题的瓶颈得到了突破.

综上，圆锥曲线的第一定义体现了“质”的区别，而第二定义则体现了“形”的统一，第一定义和第二定义的灵活转换常常是打开解析几何思路的钥匙，在题目中挖掘这些隐含信息将有助于竞赛试题的解决.另外，运用圆锥曲线的定义解题，通过数形结合，不仅能抓住问题的本质，还能避开复杂的运算，使问题巧妙获解.