2022年新高考Ⅱ卷解几题的多解、推广及变式

胡芳举

湖南省桃江县第一中学 (413400)

一、试题呈现

图1

(1)求C的方程；

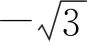
①M在AB上；②PQ∥AB；③|MA|=|MB|.

二、一题多证

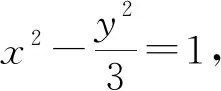
(2)选取①③⟹②.

当直线AB的斜率不存在时，显然成立.下面只考虑直线AB的斜率存在的情况.

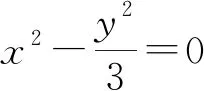
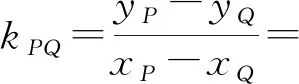
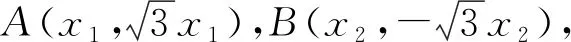
评注：证法一、二虽然思路简单自然，但运算非常复杂，学生一般有始无终.

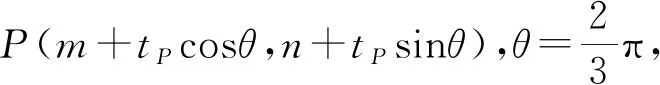
评注：证法三、四根据题设已知，灵活运用直线的参数方程、曲线系知识，简化计算，证明过程简洁巧妙，令人回味无穷.

三、试题推广

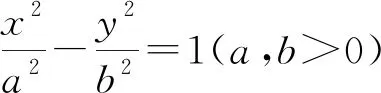
四、两个变式

图2

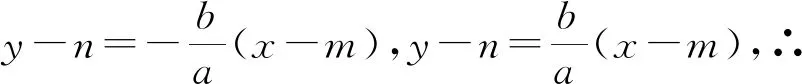
评注：过点M作直线交双曲线的两渐近线于点A，B，若点M为线段AB的中点，则C,D分别为线段OA,OB的中点，∴CD∥AB，又PQ∥CD，∴AB∥PQ，所以推广成立.

证明：设点R为线段CD的中点，由变式1易知R，M，N共线，又OCMD为平行四边形，所以O，R，M共线，故O,M,N三点共线.