基于图像特征的输电线路故障行波存续性判别

黄 杨 张广斌 王 潜 束洪春

基于图像特征的输电线路故障行波存续性判别

黄 杨 张广斌 王 潜 束洪春

（昆明理工大学电力工程学院 昆明 650500）

故障行波波头的持续存在是输电线路行波测距和行波保护等得以实施的关键。实际中存在弱故障，现有行波测距与保护缺乏自动判别故障初始波头是否存在和持续，导致行波装置产生错误结果。针对该问题，该文基于初始浪涌波形图像特征及行波在输电线路往复传播规律，提出一种输电线路故障行波波头存续性的判别方法。首先分析了故障行波波头阶跃性和后续行波的产生规律，进而提出构造与初始波头具有良好紧密型的包围盒，计算包围盒内故障行波和外切线构成面积与整个包围盒面积的饱和度，由饱和度判定初始波头的存在。进而对存在初始行波波头的情况，基于后续波头到达时序、波头幅值、斜率等相对特征，实现后续行波持续性判别。大量仿真和现场实测数据表明，该方法能够可靠判定故障行波的存续性，有效避免波头不存在的情况下行波装置的误动。

波形图像 行波 初始波头 存续性 饱和度 包围盒 输电线路

0 引言

输电线路故障后须在极短时间内实现故障线路的切除以及故障位置的准确判断，保证电力系统安全可靠运行，因此提高输电线路保护的可靠性和改善线路测距结果的稳健性对实际工程具有重要意义。行波具有响应速度快、不受线路类型及两侧系统影响等优点，在保护快速性和线路定位的精确性上具有天然的优势[1-4]，充分发掘行波的优势并将其应用于工程现场显得尤为迫切和必要。

近年来，围绕着输电线路行波保护和故障测距开展了大量卓有成效的研究[5-7]。行波保护方面，为实现对故障线路的可靠快速切除，学者从行波的频域、相似性、极性等角度展开研究。文献[8]通过对故障电流的频谱特征分析，利用固有频率主频差构造保护进而实现故障的区分；文献[9]利用形态学梯度算法提取故障行波，在此基础上利用三相初始电流行波及其模分量实现故障相区分；文献[10]分析得到首行波的表达式，利用拟合的方式提取反映故障位置的指数系数，据此提出保护方法；文献[11]通过区分故障线路本侧区外和来自对侧的故障电流在突变方向的差异提出高压直流线路单端电流暂态保护方案；文献[12]利用标准差描述暂态电压高频带Hilbert能量幅值信息和波形信息，以此构建高压直流线路保护。在行波测距方面，为可靠提高故障定位结果的稳健性，现有行波测距通过在电网中布置较多数量的数据采样点获得广域行波数据，并利用信息融合技术最终实现故障定位。文献[13]在分析网络故障行波到达时间与传输路径的匹配基础上提出利用Floyd算法简化故障网络，再通过信息融合技术计算实现故障定位；文献[14]提出利用Dijkstra算法计算故障网络中的最短路径并构建距离矩阵，在此基础上，通过融合初始行波到达时间，最终建立故障距离矩阵并对矩阵元素进行识别，最终实现网络定位的可靠性。同时，在波头标定正确的情况下，波速的准确度是影响测距结果精度最重要的因素[15-16]，因此为消除该影响，文献[17]利用行波波头到达时刻频率分量与故障距离的关系以及零模速度与频率的关系得到零模波速度；再则，为消除计算式中含有波速变量文献[18]推导了一种不受波速影响的新算法。以上方法都能在各自适用情况下实现对线路故障的快速或精确定位。然而，上述方法均是以初始波头存在为前提，在没有初始行波或仅为干扰的情况下，行波保护与测距装置可能执行错误的分析，或导致误动或报送错误的测距结果，影响了行波方法作为独立决策的可靠性。大量实测数据表明雷击未故障、山火和小故障角等非常规故障常对利用故障行波实现保护与测距的算法造成干扰。针对雷击未故障已提出很多有效的行波保护防误动方案[19-20]，而对山火、小故障角下的相关研究较少。针对此类故障研究适用于行波保护与测距的故障数据的识别方法，筛选出不具有行波波头的故障数据，无论是针对性地开展算法定制还是闭锁传统方法，对提高行波工程化应用效果均具有十分重要的价值。

本文通过分析输电线路故障行波的产生和传播规律及行波波形在图像视角下的特征，提出利用包围盒内故障波形和波形外切线构成的延拓面积的差异实现对故障初始行波存在性的判别，再利用标定的初始及后续波到达时序、波头幅值、斜率等相对特征完成对后续行波持续性的辨别。所提方法能够有效识别故障初始波头突变明显且判定为存在的行波，并且能够实现对判定初始波头或后续波头不存在的故障及时进行闭锁或发出相应告警提示，避免行波装置误动和误测。

1 输电线路故障行波特征

1.1 初始浪涌的阶跃性

输电线路发生故障时，相较故障前叠加一个反向附加电源，表现为如图1所示的一个电源单独作用于线路中，产生的暂态行波向故障线两端传播。根据叠加定理可将故障网络等效为正常网络和故障附加网络的叠加，在三相对称或单相系统下只考虑故障附加电源单独作用时，线路故障点处产生一个故障行波沿线路传播，因此对于线路端部测量装置而言，其观测到的初始浪涌往往呈现阶跃特征，并且其幅值大小如式（1）所示。式中，近似认为线路所连接波阻抗相等。

图1 故障行波的产生及传播

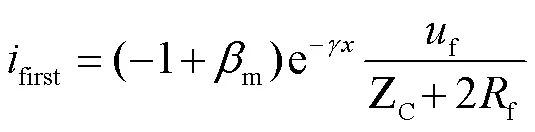
对于行波法而言，输电线路两端测量装置获取的电气量是否含有可检测的反映故障信息的行波分量是行波法能否成功应用的关键和前提。输电线路故障后故障初始波头的主要性质与附加电源及过渡电阻有关。不同故障角故障电流行波如图2所示。图2中，当故障源存在且在交流系统中故障初相角不为0°时，产生的初始浪涌为左间断右连续的阶跃型行波，沿线路向两侧传播，而当初相角为0°时不会观察到故障波头的存在。

图2 不同故障角故障电流行波

输电线路发生接地故障时按闪络通道可分为金属性接地故障与非金属接地故障。由式（1）可知，故障初始强度在不同过渡电阻下会呈现较大差异，但其初始波头的跳变特征皆会存在。在三相系统下发生单相故障时，即使三相模量不独立，其模量初始电流行波仍存在阶跃性，相应模量的表达式如式（2）所示。初始波头上升速度与波头幅值及跳变的时间相关，在同一系统下数据采样率频率一定，则在固定采样间隔下初始波头的幅值反映波头的上升速度，因此当初始波头幅值大时，波头的上升速度快，上升速度与过渡电阻负相关。

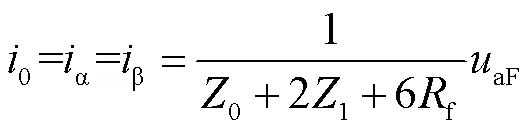
式中，aF为故障分量网路中a相电压源电压，相电流的大小a0αβ。

由以上分析可知，理论上理想情况下，当故障时故障初相角不为0°，初始波头皆会呈现跳变特征且波头的上升速度与幅值相关。但实际工程中常因行波装置通道噪声及实际故障的复杂性，在初相角为0°附近时亦难准确可靠地检测到行波波头。

1.2 故障行波持续特征

1.2.1 故障行波波头间的相对特征

对于输电线路，当故障线两端端部出线类型在故障期间维持不变，故障点持续存在且波阻抗不连续度无明显变化，折反射系数及线路传播系数不会发生变化，其在附加源作用下可观测到后续故障行波波头持续存在的特征。并且观测到的后续行波波头主要是如式（3）、式（4）所示的故障点反射波及对端母线反射于故障点的透射波。

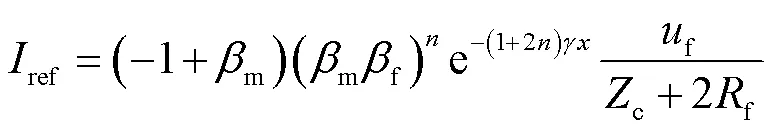
其中

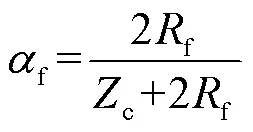
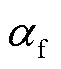
由于过渡电阻的影响，故障线路端部录波装置所采集的后续波形特征存在差异，在单相系统下由故障点折射系数f与反射系数f可知，当f=0时，f=0，f=-1，于是故障行波无法透过故障点发生折射，故无法检测到对端母线反射波，只能检测到故障行波在本侧母线与故障点发生的来回反射。而当f≠0时，有0＜f＜1，-1＜f＜0，可知故障行波可以透过故障点到达本端母线，继而在本侧可以检测到大量的对端母线反射波，但对三相系统发生单相接地故障时，由于各模量行波之间不再相互独立而发生交叉透射，但其幅值较低，对波头识别的影响不大。

依据对端母线反射波能否透过故障点到达本端母线将故障划分为强故障模态和弱故障模态。在强故障模态下，本端故障电流录波装置只会检测到本端母线与故障点之间的折反射波而无法检测到对端母线反射波，由于故障区间长度固定，在时域上故障波头会呈现出等间隔性；而在弱故障模态下，对端母线反射波会透过故障点到达本端母线，这将对故障波头的观测造成一定的干扰，考虑到对端母线的反射波呈现相反的极性，可通过极性特征作为剔除条件，排除相反极性故障波形的影响，从而使检测的故障波头呈现出等间隔的特征，并且幅值递减。

1.2.2 行波衰减畸变

输电线路故障后产生的故障行波信号是包含多种传播模式的混合信号。由于不同故障分量在传播中的衰减程度不一致使得相应行波产生畸变，因此在图像视角下可观察到相较于初始波头，后续波头呈现出平缓特征。同一波形在不同传播距离后会表现出不同程度的衰减畸变，且越往后越明显。如图2中所示的90°故障角下，其初始波头斜率相较于后续到达的波头而言明显较大，斜率越小对应着行波的衰减程度越大。故障行波在线路上的传播特性可由传播系数表示，其表达式为

故障行波传播时的幅值衰减系数和相位滞后系数的表达式为

式中，0、0、0、0和分别为单位线路长度的电阻、电导、电感、电容以及角频率，由此描述故障行波在传播过程中的幅值衰减以及相位变化。

在PSCAD/EMTDC中搭建如图1所示的仿真模型，故障位置距观测点60km处，通过改变故障过渡电阻大小仿真强弱两类故障模态的波形，且在输电线路模型中两侧母线均为多回出线，仿真波形如图3所示。

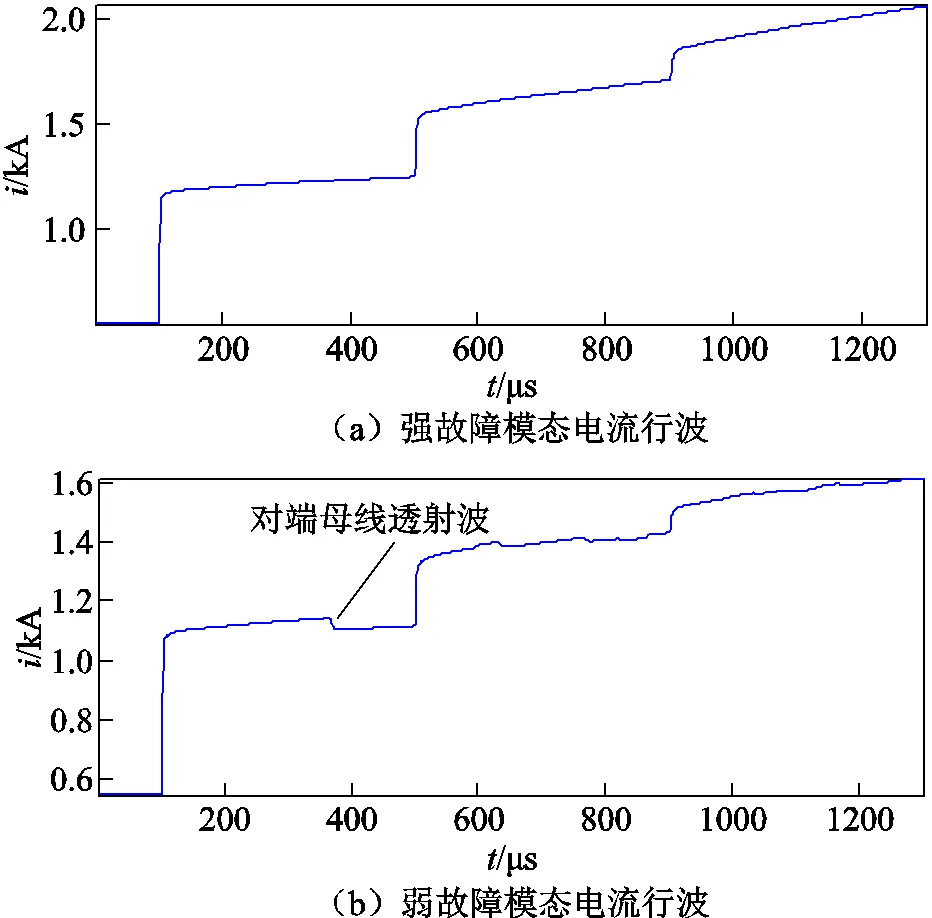
图3 典型故障下行波仿真波形

由图3可见，故障发生后故障行波在故障点与母线之间发生来回的折反射，且由于外部故障条件未发生变化，在强故障模态下故障行波在各自独立区域来回传播，故障波头表现出规律的间隔，且幅值和斜率递减；在弱故障模态下，剔除相反极性反射波的影响使之呈现强故障模态特征的到达时间等间隔和幅值、斜率递减的规律。

2 基于图像特征的故障行波存续性判别

2.1 基于图形围盒饱和度的故障初始波头辨识

行波分析的本质是利用波头形态相对变化特征，对绝对幅值不甚关注，并且考虑到行波信号较弱、受噪声影响大，基于数据的微观奇异性容易陷入局部极值点进而导致误判。故本文于波形图像上进行波形形态特征的存续性判别，采用图形化显示故障行波，该方式能够突出波形宏观特征、去标度化。

故障电流行波的图形化通过对故障数据作图完成。对一定量的故障波形数据图形化，其轴在能清楚地观测到相应特征情况下，分辨率越高，对应的行波波头跳变特征越缓，轴分辨率对应其波头幅值显示大小且呈正相关。映射到视窗的两轴坐标比例受观测物的影响，其关系为[21]

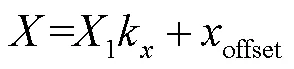
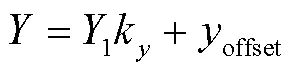
式中，、为在窗口中显示的像素；1、1分别为行波波形数据对应的采样点、幅值；k、k分别为在规定分辨率下除去偏移量的数值与波形时间和波形幅值差的比值；offset、offset为窗口基准点的偏移量。本文将故障行波映射到像素分辨率为900×1 200下完成行波数据的显示。考虑图窗左右、上下的固定边距，取offset为156，offset取轴分辨率的中点与原波形起点位置归算到像素的差值。

对采集的故障行波数据以图形化方式显示，以机器模拟人工视角观察其突变特征，并由前文分析可知，故障后在附加电源的作用下，故障行波波头呈现阶跃突变，因此通过算法标定，检测初始波头外切线与波形图像之间是否存在一定面积以实现对故障存续性的初始辨别。不同故障行波面积特征如图4所示。图4中，在合理视窗中利用分段线性化逼近方法标示出其波形变化程度较大的兴趣区域，在该区域内可明显观察到故障行波跳变的过程。进而借助包围盒思想构造与兴趣区域几何对象具有良好紧密性的三角包围盒区域，该包围盒可在最小限度表达目标的性质。对于存在行波波头的故障，其在包围盒内的图像与包围盒外切线之间几乎不存在面积，而不存在行波波头的故障其所围的面积表现出显著不同的特征。机器视角中的饱和度变量是描述目标区域在围盒中充满程度的理想参数，对此可利用饱和度反映故障行波与围盒外切线形成的延拓区域面积与包围盒面积的比值[22]，可得

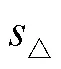
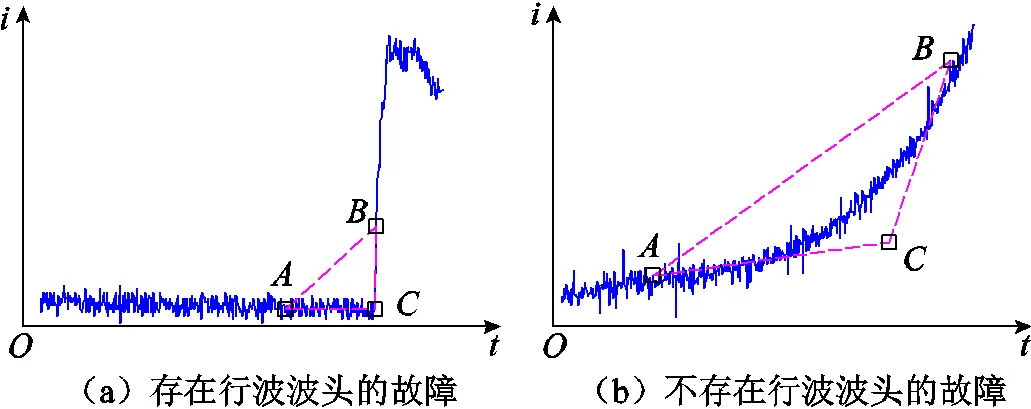
图4 不同故障行波面积特征

对于三角包围盒，当确定其三个顶点的坐标（1,1）、（2,2）和（3,3）可计算其面积为

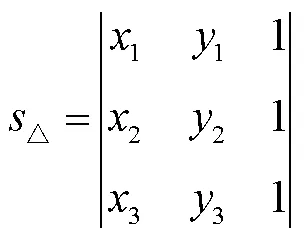
对围盒中波形与外切线的面积，其中行波波形可用函数()表示，而直线的函数()可由、两点的坐标表示。

则两部分面积之差可由式（13）表示。

将式（13）代入式（10）可得围盒饱和度表达式为

在实际中，对于式（14）可借助计算机视觉技术于不同连通域填入不同的颜色，通过统计相同颜色的像素点得到该区域颜色的面积，从而简便地实现延拓区域饱和度的计算。

对于存在初始行波的故障波形，初始行波附近阶跃特征明显，与围盒逼近度高，延拓区域饱和度趋近于0；对不存在初始行波的如过零点、山火高阻时变等复杂故障波形，阶跃特征不显著，呈现缓变的特征，延拓区域饱和度较高。据此特征，形成故障初始波头不存在的判据，即

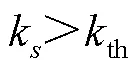
式中，th为饱和度阈值。

正常情况下，初始浪涌标定的延拓区域饱和度理论上为0，因此饱和度阈值th在理论上可为接近0的很小的正数，但考虑到故障波形的复杂性，整定时需留有一定裕量防止误判，大量实测数据和含噪声的数字仿真测试表明，存在初始行波和不存在初始行波的延拓区域饱和度差异显著，th取0.1即能满足实际需要。

由以上分析可知，对于确定的、、三点采用上述饱和度计算可实现故障初始波头的辨识，因此、、三点的获得成为关键。此外，考虑到在不同视窗尺度下整体故障波形图像对初始波头延拓的图像面积特征呈现较大的差异，当视窗过大时对于故障关键特征的辨识可能会出现较大误差，因此需要合适的视窗尺度避免对阶跃性质的错误辨识。考虑到算法在进行原始录波数据标定中因为数据视窗不同而产生不同的误差，文献[23]所提算法能够在一定角度范围内实现直线的标定，本文采用该算法首先利用初次标定在行波突变点前后得到相应标定直线，规定突变点前的标定直线1的线段两端的坐标为1、2，突变点后的标定直线2线段两端的坐标为1、2，直线标定结果如图5所示。

图5 直线标定效果

通过标定直线1的端点坐标1、2可求得直线方程A，同理可获得标定直线2的直线方程B，所获得的两条直线方程表达式可用线性方程组表示为

对所获的两条直线方程，通过联立可计算得到两直线方程的交点，取位于交点前的1、2两点中坐标较小的点作为点，位于交点后的1、2两点中坐标较大的点作为点。

在、、点确定的基础上，考虑到初始波头跳变特性在突变点后较短视窗内即可观测到该性质全貌，因此可取较小数据窗，而对突变点前需要截取一定数据，保证突变前后信号的完整性。以1MHz采样率获得的现场实测220kV线路故障电流行波为例，利用首次标定延长的交点，在该点截取前500μs及后100μs数据保证合理的视窗如图6b，较之大视窗图6a相比，保留了初始波头宏观特征的同时，有着更好的分辨率，有助于提升判据的区分度。

图6 不同视窗下包围盒区域标定

2.2 基于时序检测的故障行波持续性检测

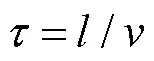
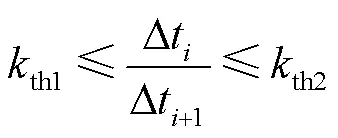
式中，th1、th2为判定到达的两组故障相邻波头等间隔的阈值，理论上th1、th2都为1，但考虑到行波衰减、畸变等因素，以及本阶段波头标定的宏观性，标定时刻存在误差，为增强条件的适用性，取th1为0.7、th2为1.3。

3）在标定波头获得到达时刻和幅值的同时还可得到因线路衰减而递减的斜率，根据标定波头的顺序定义为1,2,3,。初始波头的衰减程度相较后续到达波头最低，因此选取初始波头为基准值量化波头之间的关系，如式（19）所示。

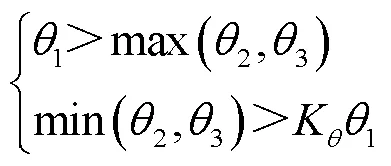
式中，K为门槛值，综合考虑输电线路长度和多次折反射导致的衰减和色散，以及大量实测故障行波波头陡度人工直观感受下的可识别性，取K为0.4。

当后续波头到达时序关系、幅值关系、斜率关系满足式（17）～式（19）时，判定故障后续行波持续存在。否则，判定为不存在，此情况下闭锁基于单端后续行波波头的保护和测距装置。需要指出，上述三元组特征阈值是考虑到实测波形存在的差异性及算法标定误差后进行松弛选定的，此门槛值并非绝对固定，可根据实际运行情况动态调整。

综上所述，对每次故障产生的行波而言，行波录波装置采集到的故障波形形态主要与附加故障源以及输电线路本身的特性有关；而在剔除因透射过渡电阻的影响后，故障行波在传播过程中相邻波头之间呈现出规律间隔主要与故障距离有关；其附加故障源决定故障行波的初始形态，理论上当故障角不为0°时初始行波波头呈现阶跃的形态，且后续呈现等间隔性。先基于首波头标定其延拓区域实现行波波头存在性判别，进而再通过后续波头的三元组特征判别故障的持续性，最终实现故障行波存续性判别，按此思路可形成故障行波存续性判别算法流程如图7所示。

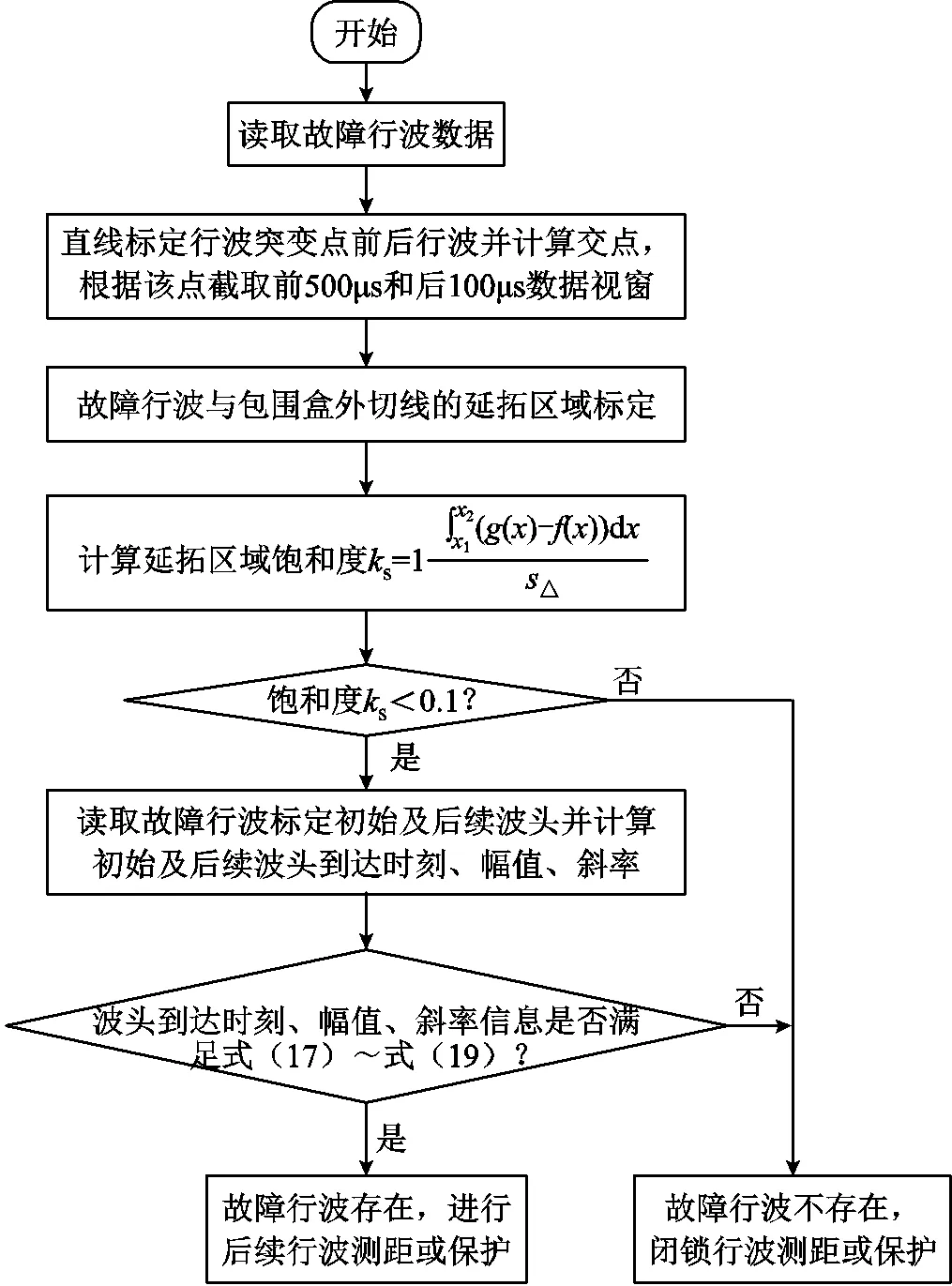
图7 算法流程

3 应用实例与算法适应性分析

3.1 应用实例

3.1.1仿真算例

基于PSCAD/EMTDC搭建图1所示的220kV输电线路模型，输电线路配置如附图1所示，故障线路MN全长100km，其M侧母线设置4回出线，N侧3回出线，故障设置于距M侧观测点60km处发生A相接地故障，其中故障角为30°，过渡电阻为50Ω，在仿真数据中加入10%噪声所获故障电流波形如图8所示。

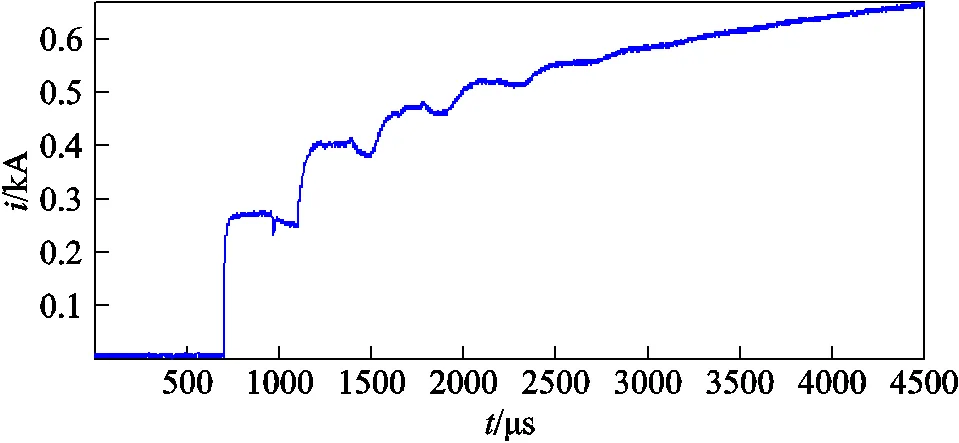
图8 故障电流行波仿真波形

利用算法标记故障初始波头得到合适的视窗截取位置，进而根据该位置参数截取固定视窗进行饱和度计算，其合理视窗如图9a所示。根据式（10）可知，应计算该故障初始波头与围盒之间的延拓面积与整个包围盒面积的比值，求得该延拓区域的饱和度s=0.008 4，根据所取阈值th=0.1可知该初始波头判定为存在，由此进行算法后续流程，即初始波头与后续有效波头的持续性判别。后续故障波头持续性判别应以初始波头为基准进行标定，后续波头标记结果如图9b所示。

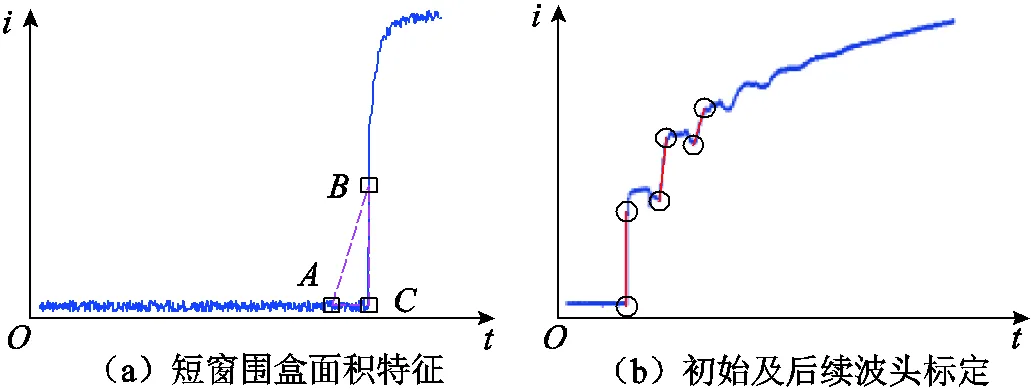
图9 存续性面积特征及波头标定结果

在4时长内标定出的有效波头数为3，其标定波头的到达时刻、幅值、标定斜率见表1。进一步计算可得到含时序关系、幅值关系、斜率关系的结果见表2。该故障行波存续性判定结果为存续，表格中的到达时间、幅值均为对应图像像素值，斜率单位为°。由上述可知，初始波头应首先满足面积特征，对于判定为存在初始行波的故障还需考虑故障行波波头在输电线路往复传播过程中端部电流行波录波装置所记录的故障数据，通过分析相邻波头到达时序从而确定故障波头的等间隔性。该行波波形规律性较强，所提机器判定方法与人工直观感受一致，适宜采用行波保护或行波测距。

表1 仿真故障行波波头标定结果

Tab.1 Wavefront calibration results for simulated traveling wave data

表2 仿真故障行波三元组特征计算结果

Tab.2 Results of calculated triple feature for simulated traveling wave data

3.1.2 实测算例1

2009年10月30日某220kV线路发生单相接地故障，1MHz采样率下故障相电流行波录波如图10所示。

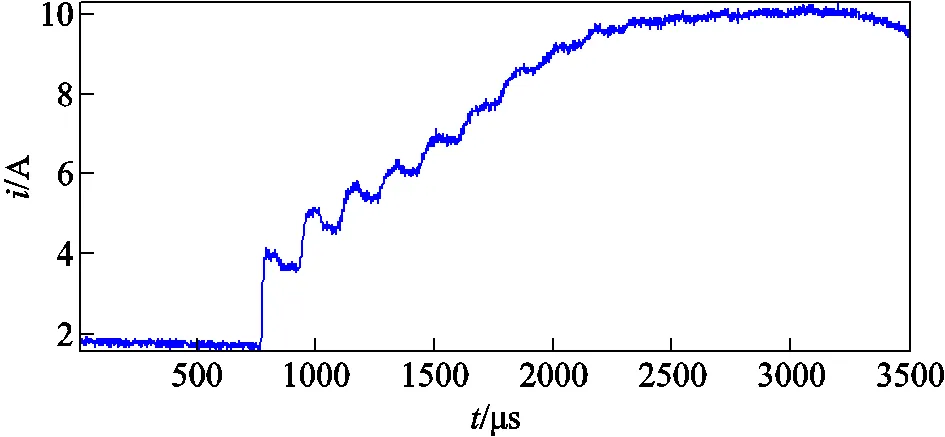
图10 220kV输电线路故障电流录波

计算得到其延拓区域与整个包围盒面积的饱和度k=0.005 4，其包围盒标定结果如图11a所，根据所设阈值可知，该延拓区域饱和度满足初始波头阶跃特征，应进行后续波头的标定，其最终标定结果如图11b所示。

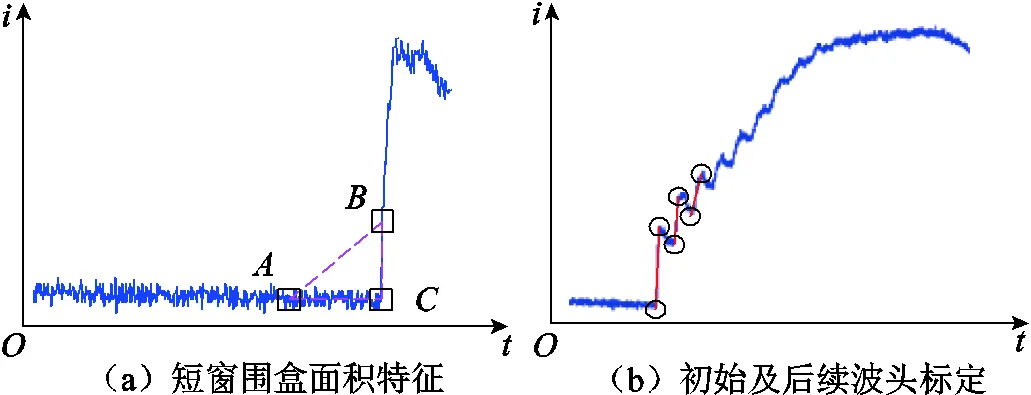
图11 实测故障面积特征及波头标定结果

通过标定可得表3的波头标定结果，再计算得到的波头数据信息可得到表4所示的三元组计算结果，该故障行波判定为存续，适宜应用行波算法，实际行波测距装置也对该故障成功进行了测距。

表3 实测故障行波波头标定结果

Tab.3 Results of detection of measured fault traveling wave data

表4 实测故障三元组计算结果

Tab.4 Results of measured traveling waves’ triple features

3.1.3 实测算例2

2011年1月12日某220kV线路发生故障，1MHz采样率下得到的电流行波波形如图12所示，选用文献[23]所述的算法进行波头标定会得到如图13所示的结果，根据图像标定结果，其对应的初始及第二个波头时间差为913.179 4μs，取波速=0.298km/μs，则对应的故障位置为136.063 7km，该故障位置已经超过该条线路的全长93.11km，测距结果发生错误。

图12 山火故障电流行波

图13 Hough算法波头标定结果

按照本文所提方法根据初次标定结果首先截取合适视窗判断延拓区域面积的饱和度，截取的合适视窗面积特征标定结果如图14所示，通过计算得到延拓区域面积的饱和度k=0.206 6，由此可知不满足算法初始条件即不符合故障行波初始波头的阶跃性质，继而得到该条故障信息不适用于行波测距算法，闭锁后续行波测距流程，避免了误测。

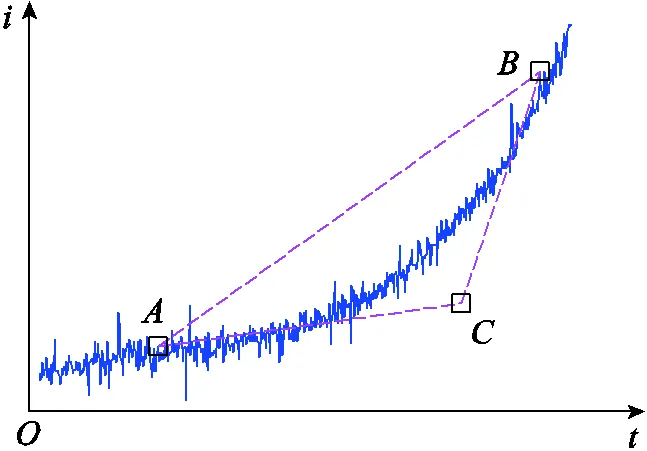
图14 山火故障短窗围盒面积特征

3.2 算法适应性分析

采用本文所提判别方法，通过对实测数据的验证以及在PSCAD/EMTDC下对如图1模型进行仿真，通过改变故障类型、过渡电阻大小、故障角角度以及施加噪声强度以验证所提方法的有效性，故障行波存续性判别结果见表5，该表故障行波数据的采样率均为1MHz，受篇幅所限，故障信息标定的到达时刻、幅值、标定斜率等数据列于附录附表1。

考虑到对故障行波个体而言，其波形形态主要与故障位置及过渡电阻有关。为验证故障强度对所提方法的影响，在距离M端设置10km、30km、50km和80km的故障如表5中编号1、2、3、4的数据所示，以及不同的过渡电阻0Ω、50Ω、100Ω及150Ω故障。结果表明所提算法对不同故障距离、不同过渡电阻均有效。

为验证算法在复杂环境中的适应性，在仿真得到的波形中添加不同的噪声。考虑实际工程运行中故障发生时故障角都偏大，通过比较编号1、2、5、11所示几种在较大故障角下不同噪声情况的故障行波存续性辨识结果可知，在不同噪声情况下所提方法对于幅值偏差、斜率偏差以及时序偏差都能良好适应。而当故障角较小时发生故障如编号8、9所示，在无噪声情况下该方法也能适应，仅当噪声干扰较为严重的情况下，由于噪声将故障波头淹没无法得到该初始波头面积特征，因而会造成影响。同时，为了验证算法在不同故障类型中的适应性，分别设置单相接地故障，两相短路故障、两相接地短路故障以及三相短路故障（编号1、10、11、12），其结果见表5，可见该方法适用于不同类型故障。而对于编号13、14、15、16、17、18所示的实测数据，运用本文算法亦能可靠判别其存续性。同时，对于标定结果为存在的故障行波在后续的测距过程中能够准确判断故障位置，如图15所示的编号16的样本结果。

表5 故障行波存续性判别结果

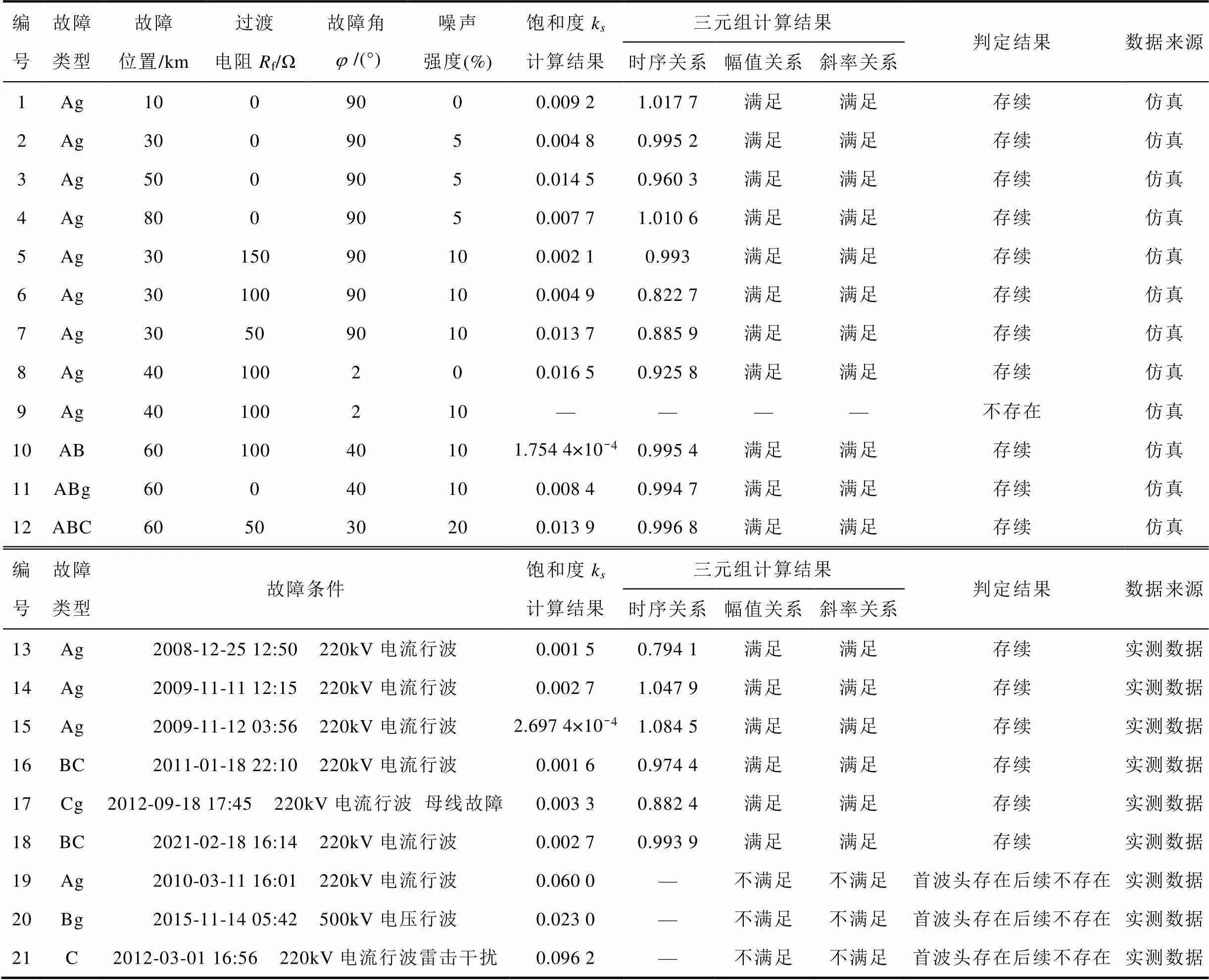
Tab.5 Result of identification of the existence and persistence of fault induced traveling waves

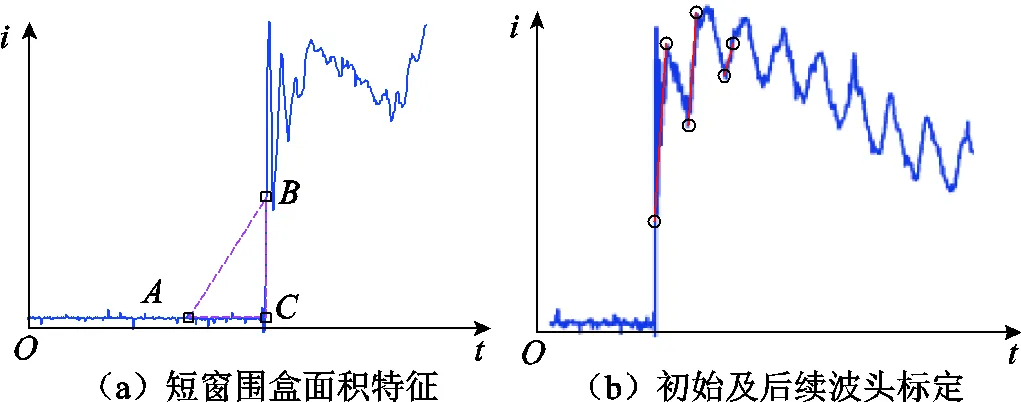
图15 16号故障样本面积特征及波头标定结果

对于编号19的实测数据，其故障初始波头能判定出存在，但故障行波在后续的持续性判定中不满足条件故而判定为首波头存在后续不存在，此类故障适用于双端测距，而对于单端测距应当闭锁，其故障波形和面初始积特征标定如图16所示。对于编号20的500kV电压行波实测数据，如图17a所示，本文所提方法也能够标定出其初始波头，其标定的面积特征结果如图17b所示，但后续波头的标定因来自不同线路的反射波先后到达，规律性较差，无法通过后续行波的相对关系判别故障点的持续性，故电压行波更加适用于双端测距。

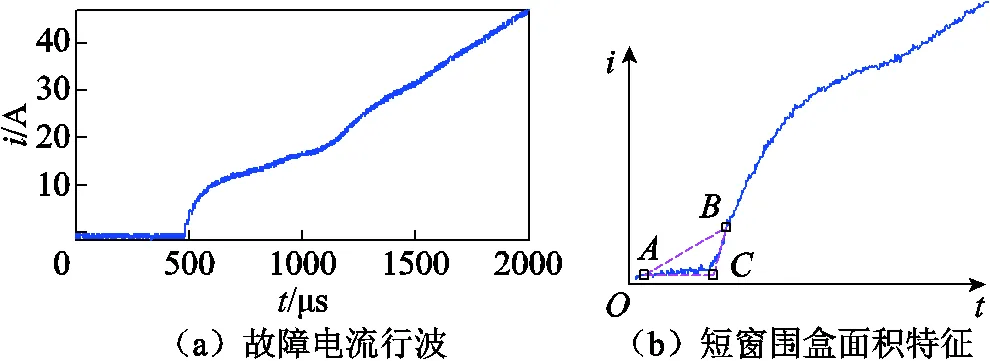
图16 19号故障样本波形及围盒面积特征

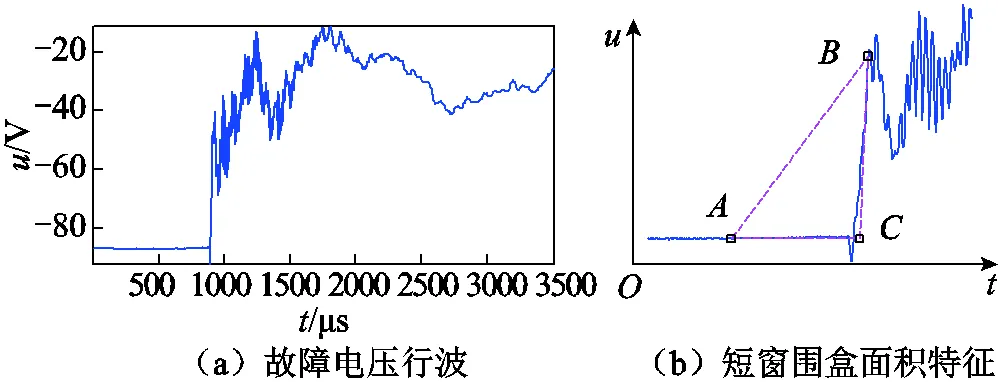
图17 20号故障样本波形及围盒面积特征

对如图18所示的21号实测雷击干扰样本而言，用本文所提方法对其初始波头进行辨识发现能够满足初始波头所述饱和度，判定初始波头为存在。但雷击干扰后续没有稳定的工频短路电流分量，且不能够标定出后续波头，故应闭锁单端测距装置。若双侧初始波头均存在，则可以使用基于双端初始行波的双端测距定位雷击点位置。

图18 21号雷击干扰波形及围盒面积特征

综上所述，本文所提方法对不同故障位置、故障距离、故障过渡电阻、不同类型的行波信号均具有良好的适用性，依靠饱和度计算结果，判定初始波头是否存在，筛选出适于基于初始波头的双端测距式保护、测距和多端测距的行波数据，进而根据后续行波的时序、幅值和斜率的相对特征，进一步判定后续故障点反射波的持续存在性，为进行单端测距和保护筛选出适用的数据，有效地避免了因波头不存在导致的算法误启动和误测。所识别出的异常故障样本也为后续定制化的行波算法设计或优化提供了重要数据源。

4 结论

针对原有行波保护与测距缺乏自动判别故障初始波头及其后续波头是否存在的不足，本文通过分析故障行波初始波头跳变特征及后续波头间隔规律，提出基于行波波形图像特征的输电线路故障存续性判别方法，得出以下结论：

1）输电线路故障，当故障附加源的存在时，使得信号产生突变，波形上呈现阶跃跳变特征，故障线两端端部出线类型在故障期间维持不变，故障点持续存在且波阻抗不连续程度无明显变化，故障行波波形存在重复性和自相似性。

2）在能观测到波形数据跳变过程的合理视窗内，对故障波形折线化逼近并构造出与兴趣区域具有紧密联系的三角包围盒，利用饱和度表征该故障波形与标定直线形成的延拓区域与包围盒面积的比值辨识初始波头存在性。

4）对于大多数输电线路，其两侧母线均为多回出线，通过不同极性区分故障点反射波与对端母线反射波，从而不影响对故障波头间续特性的判别。对少数发电厂—变电站的单出线-多进线情况，所提初始波头存在性判据仍有效，但此类拓扑对端反射和故障点反射的波头极性一致，基于后续波头间隔性的判据将失效，有待后续进一步研究。

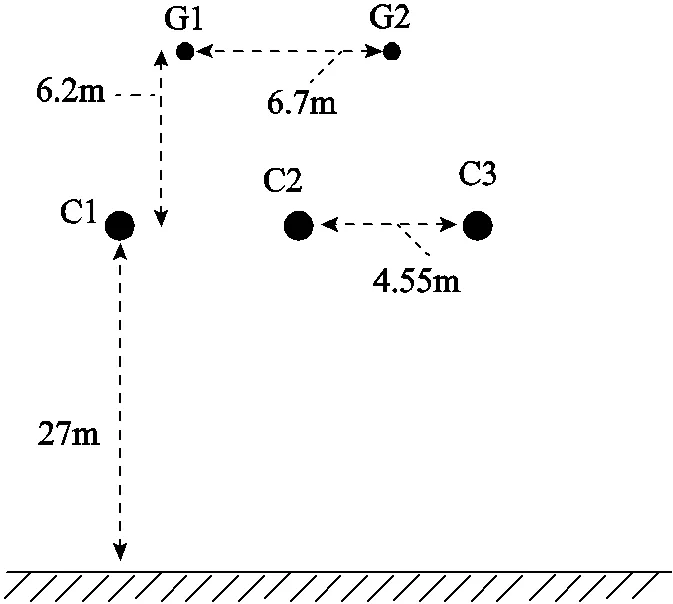
附图1 输电线路配置

App.Fig.1 Transmission line configuration

附表1 故障行波波头到达时刻、幅值、斜率计算结果

App.Tab.1 Results of fault traveling waves’ arrival time, amplitude, and slope

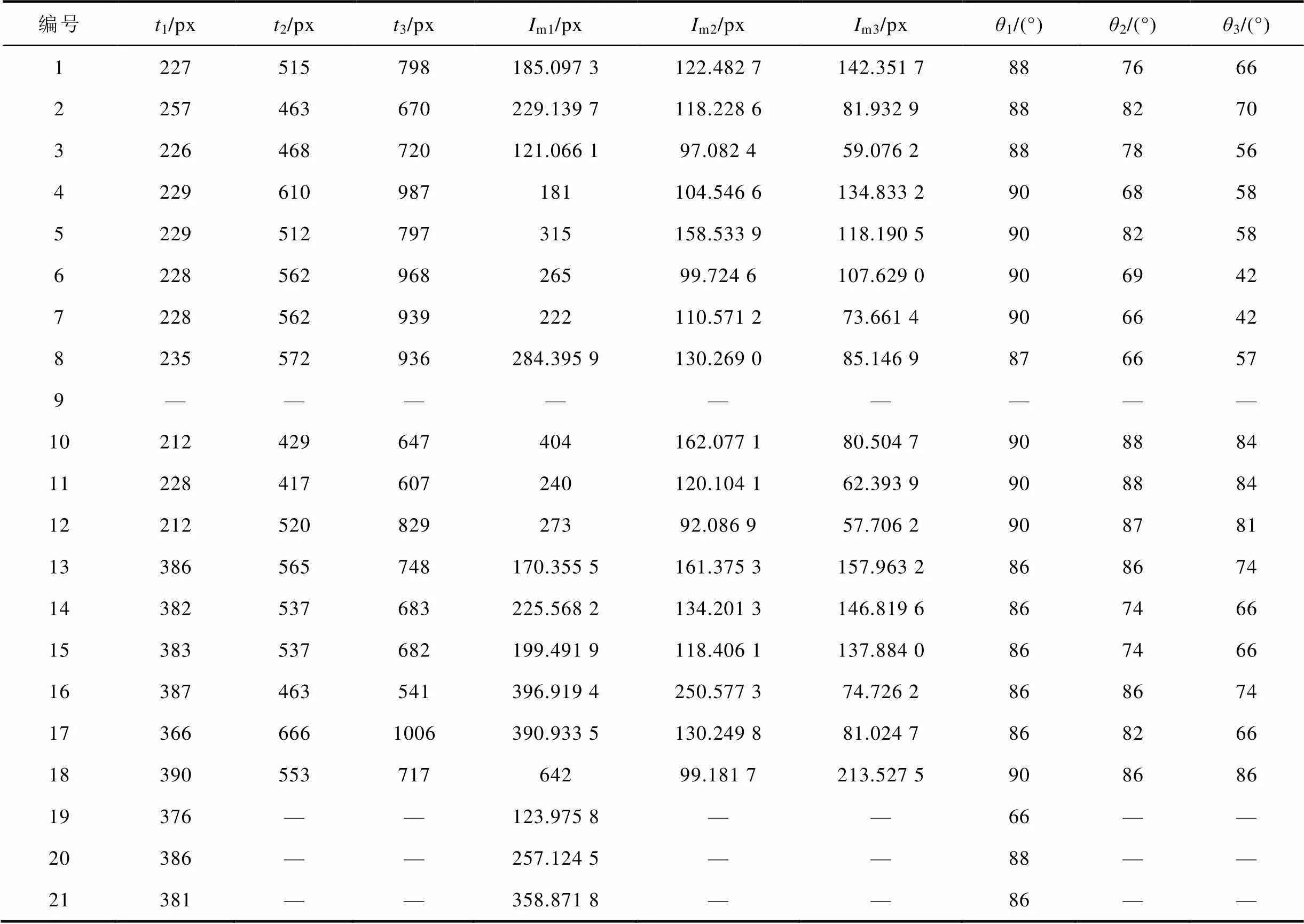
编号t1/pxt2/pxt3/pxIm1/pxIm2/pxIm3/pxθ1/(°)θ2/(°)θ3/(°) 1227515798185.097 3122.482 7142.351 7887666 2257463670229.139 7118.228 681.932 9888270 3226468720121.066 197.082 459.076 2887856 4229610987181104.546 6134.833 2906858 5229512797315158.533 9118.190 5908258 622856296826599.724 6107.629 0906942 7228562939222110.571 273.661 4906642 8235572936284.395 9130.269 085.146 9876657 9————————— 10212429647404162.077 180.504 7908884 11228417607240120.104 162.393 9908884 1221252082927392.086 957.706 2908781 13386565748170.355 5161.375 3157.963 2868674 14382537683225.568 2134.201 3146.819 6867466 15383537682199.491 9118.406 1137.884 0867466 16387463541396.919 4250.577 374.726 2868674 173666661006390.933 5130.249 881.024 7868266 1839055371764299.181 7213.527 5908686 19376——123.975 8——66—— 20386——257.124 5——88—— 21381——358.871 8——86——

注：表格中行波到达时刻、行波幅值均为对应图像像素值。

[1] Korkali M, Lev-Ari H, Abur A. Traveling-wave-based fault-location technique for transmission grids via wide-area synchronized voltage measurements[J]. IEEE Transactions on Power Systems, 2012, 27(2): 1003-1011.

[2] Naidu O, Pradhan A K. A traveling wave-based fault location method using unsynchronized current measurements[J]. IEEE Transactions on Power Delivery, 2019, 34(2): 505-513.

[3] 邓丰, 梅龙军, 唐欣, 等. 基于时频域行波全景波形的配电网故障选线方法[J]. 电工技术学报, 2021, 36(13): 2861-2870. Deng Feng, Mei Longjun, Tang Xin, et al. Faulty line selection method of distribution network based on time-frequency traveling wave panoramic waveform[J]. Transactions of China Electrotechnical Society, 2021, 36(13): 2861-2870.

[4] Zhang Chenhao, Song Guobing, Wang Ting, et al. Single-ended traveling wave fault location method in DC transmission line based on wave front information[J]. IEEE Transactions on Power Delivery, 2019, 34(5): 2028-2038.

[5] 于华楠, 马聪聪, 王鹤. 基于压缩感知估计行波自然频率的输电线路故障定位方法研究[J]. 电工技术学报, 2017, 32(23): 140-148. Yu Huanan, Ma Congcong, Wang He. Transmission line fault location method based on compressed sensing estimation of traveling wave natural frequencies[J]. Transactions of China Electrotechnical Society, 2017, 32(23): 140-148.

[6] 李斌, 张纪航, 刘海金, 等. 基于波形相似度分析的直流输电线路故障测距[J]. 电力自动化设备, 2019, 39(9): 27-32, 53. Li Bin, Zhang Jihang, Liu Haijin, et al. Fault location of HVDC transmission lines based on waveform similarity analysis[J]. Electric Power Automation Equipment, 2019, 39(9): 27-32, 53.

[7] 戴志辉, 刘自强, 刘雪燕, 等. 基于首行波曲率的柔性直流输电线路单端量保护[J]. 电工技术学报, 2021, 36(9): 1831-1841. Dai Zhihui, Liu Ziqiang, Liu Xueyan, et al. Single-ended protection for flexible DC transmission line based on curvature of initial traveling wave[J]. Transactions of China Electrotechnical Society, 2021, 36(9): 1831-1841.

[8] 李小鹏, 何正友, 陈双, 等. 基于电流行波固有频率的输电线路纵联保护方法[J]. 中国电机工程学报, 2013, 33(28): 121-129, 19. Li Xiaopeng, He Zhengyou, Chen Shuang, et al. A novel pilot protection for transmission lines based on natural frequencies of current[J]. Proceedings of the CSEE, 2013, 33(28): 121-129, 19.

[9] 薛士敏, 崔淼. 基于形态学梯度算法的微电网行波保护方案[J]. 电力系统保护与控制, 2019, 47(2): 31-39. Xue Shimin, Cui Miao. Current traveling wave based protection scheme for microgrids using morphological gradient algorithm[J]. Power System Protection and Control, 2019, 47(2): 31-39.

[10] 张晨浩, 宋国兵, 董新洲. 利用故障电流首行波拟合的柔性直流输电线路单端行波保护原理[J]. 中国电机工程学报, 2021, 41(8): 2651-2660. Zhang Chenhao, Song Guobing, Dong Xinzhou. Principle of non-unit traveling wave protection for VSC-HVDC transmission line using fault current initial traveling wave fitting[J]. Proceedings of the CSEE, 2021, 41(8): 2651-2660.

[11] 陈仕龙, 张杰, 刘红锐, 等. 特高压直流输电线路单端电流方向暂态保护[J]. 电工技术学报, 2016, 31(2): 171-177. Chen Shilong, Zhang Jie, Liu Hongrui, et al. A single-ended current direction transient protection of UHVDC transmission line[J]. Transactions of China Electrotechnical Society, 2016, 31(2): 171-177.

[12] 樊艳芳, 王永进. 基于Hilbert能量幅值信息和波形信息的特高压直流输电线路单端保护方法[J]. 电工技术学报, 2021, 36(9): 1818-1830. Fan Yanfang, Wang Yongjin. Single-ended protection method for UHVDC transmission line based on Hilbert energy amplitude information and waveform information[J]. Transactions of China Electrote-chnical Society, 2021, 36(9): 1818-1830.

[13] 邓丰, 曾祥君, 陈楠, 等. 自适应网络结构的故障行波定位方法[J]. 电力系统自动化, 2009, 33(19): 66-70. Deng Feng, Zeng Xiangjun, Chen Nan, et al. A network-adapted traveling-wave fault location method[J]. Automation of Electric Power Systems, 2009, 33(19): 66-70.

[14] 李泽文, 唐平, 曾祥君, 等. 基于Dijkstra算法的电网故障行波定位方法[J]. 电力系统自动化, 2018, 42(18): 162-168. Li Zewen, Tang Ping, Zeng Xiangjun, et al. Method of traveling wave fault location based on Dijkstra algorithm in power grid[J]. Automation of Electric Power Systems, 2018, 42(18): 162-168.

[15] 位韶康, 陈平, 姜映辉. 一种不受波速影响的单端行波测距方法[J]. 电力系统保护与控制, 2013, 41(13): 76-81. Wei Shaokang, Chen Ping, Jiang Yinghui. A single-ended traveling wave ranging method avoiding wave speed influence[J]. Power System Protection and Control, 2013, 41(13): 76-81.

[16] 张怿宁, 徐敏, 刘永浩, 等. 考虑波速变化特性的直流输电线路行波故障测距新算法[J]. 电网技术, 2011, 35(7): 227-232. Zhang Yining, Xu Min, Liu Yonghao, et al. A novel travelling wave fault location algorithm for HVDC transmission lines considering variation characteristics of wave speed[J]. Power System Technology, 2011, 35(7): 227-232.

[17] 唐金锐, 尹项根, 张哲, 等. 零模检测波速度的迭代提取及其在配电网单相接地故障定位中的应用[J]. 电工技术学报, 2013, 28(4): 202-211. Tang Jinrui, Yin Xianggen, Zhang Zhe, et al. Iterative extraction of detected zero-mode wave velocity and its application in single phase-to-ground fault location in distribution networks[J]. Transactions of China Electrotechnical Society, 2013, 28(4): 202-211.

[18] 高艳丰, 朱永利, 闫红艳, 等. 一种新型的输电线路双端行波故障定位方法[J]. 电力系统保护与控制, 2016, 44(8): 8-13. Gao Yanfeng, Zhu Yongli, Yan Hongyan, et al. A new fault location method of transmission lines based on double-terminal traveling wave[J]. Power System Protection and Control, 2016, 44(8): 8-13.

[19] 代杰杰, 刘亚东, 姜文娟, 等. 基于雷电行波时域特征的输电线路雷击类型辨识方法[J]. 电工技术学报, 2016, 31(6): 242-250. Dai Jiejie, Liu Yadong, Jiang Wenjuan, et al. Identification of back striking and shielding failure on transmission line based on time domain characteristics of traveling wave[J]. Transactions of China Electro-technical Society, 2016, 31(6): 242-250.

[20] 吕哲, 王增平. 基于暂态波形特征的输电线路雷击干扰与故障识别方法[J]. 电力系统保护与控制, 2020, 48(6): 18-26. Lü Zhe, Wang Zengping. Identification of lightning strike disturbance and faults for transmission line based on transient waveform characteristics[J]. Power System Protection and Control, 2020, 48(6): 18-26.

[21] 程晓畅, 潘仲明, 王跃科. 基于Windows图形环境的采集数据波形重建方法[J]. 计算机测量与控制, 2005, 13(6): 609-611. Cheng Xiaochang, Pan Zhongming, Wang Yueke. Method of rebuilding signal figure of acquisition data based on Windows graphic setting[J]. Computer Automated Measurement & Control, 2005, 13(6): 609-611.

[22] 章毓晋. 计算机视觉教程: 微课版[M]. 3版. 北京: 人民邮电出版社, 2021.

[23] 张广斌, 束洪春, 于继来. 基于Hough变换直线检测的行波波头标定[J]. 中国电机工程学报, 2013, 33(19): 165-173, 6. Zhang Guangbin, Shu Hongchun, Yu Jilai. Surge identification for travelling wave based on straight lines detection via Hough transform[J]. Proceedings of the CSEE, 2013, 33(19): 165-173, 6.

Identification of the Existence and Persistence of Faulted Traveling Waves for Transmission Lines Based on Image Features

（Faculty of Electric Power Engineering Kunming University of Science and Technology Kunming 650500 China）

Nowadays, there have been a lot of research achievements around traveling wave protection and fault location for transmission lines. All these research achievements are based on the premise that the initial surge exists. However, in some cases there is no initial surge, such as weak faults. It is necessary to identify such cases automatically, so that the traditional traveling wave methods can be blocked, and the customized algorithm can be implemented. However, there is no approach to identifying the existence of fault traveling waves. In order to solve this problem, based on the characteristics of initial surge waveform and the regularity of traveling wave propagation on transmission lines, an approach is proposed to identifying the existence and persistence of traveling wavefront of transmission line faults from the perspective of digital waveform image in the paper.

Firstly, the generation, propagation and catadioptric process of fault induced traveling waves in AC transmission lines are analyzed. There is a rapid change of the initial wavefront under the action of the fault excitation source, when the fault occurs on the transmission line. And the interval between the initial surge and the subsequent wavefronts is equal, by eliminating the interference of the refraction waves according to the slope of the wavefront.

Secondly, a bounding box with good compactness with the initial rapid change is constructed.The area which is composed by the fault traveling wave and the outer tangent line in the bounding box is computed. The saturation of the bounding box is calculated according to the ratio of the computed area and the entire area of the bounding box. The existence of the initial traveling wavefront is determined by the saturation value.

Finally, when there is an initial traveling surge, the initial and subsequent wavefronts are calibrated and normalized. The interval between each wavefront is quantized through the triplet data information containing the deviation of wavefront amplitude, the deviation of arrival timing, and the deviation of slope. The persistence of the subsequent traveling waves is identified according to the calculated triplet deviation.

A large number of digital simulations and actual fault data record have shown that the initial fault traveling wavefront does not exist when the saturation of bounding box is greater than 0.1. The corresponding traveling wave algorithm can realize blocking and avoid maloperation of traveling wave devices. When the saturation is less than or equal to 0.1 and the subsequent calibrated wavefronts’ quantification meets the threshold requirements, the traveling wave fault location methods can correctly determine the fault location. In addition, the proposed method is insensitive to current data or voltage data and can operate correctly.

The following conclusions can be drawn: (1) When there is an additional source of fault in the transmission line, the waveform shows a step jump feature. The type of outgoing line at both ends of the fault line remains unchanged during the fault. The fault point persists and the discontinuity of surge impedance has no obvious change. The fault traveling wave shape has repeatability and self-similarity. (2) In a reasonable window where the waveform of the rapid change process can be observed, the fault waveform is approximated linearly and a triangle bounding box closely related to the region of interest is constructed. The saturation of the bounding box can be used to identify the existence of the initial surge. (3) The initial wavefront and the subsequent arrival wavefronts are characterized by the calculated ternary results, and the fault traveling wave persistence can be determined by evaluating the ternary data information of the fault traveling wavefronts.

Waveform image, traveling waves, initial surge, existence and persistence, degree of saturation, bounding box, transmission line

国家自然科学基金（51907085）和云南省重大科技专项计划（202002AF080001）资助项目。

2021-11-01

10.19595/j.cnki.1000-6753.tces.211761

TM77

黄 杨 男，1994年生，硕士研究生，研究方向为新型继电保护与故障测距。E-mail：1161470272@qq.com

张广斌 男，1985年生，博士，副教授，硕士生导师，研究方向为新型继电保护与故障测距。E-mail：guangbin85@gmail.com（通信作者）

2022-03-02

（编辑 郭丽军）