绳驱动柔性机器人运动学建模及主从控制研究*

朱 靖,齐 飞,佘世刚,张 恒,裴海珊

(常州大学 机械与轨道交通学院,江苏 常州 213016)

0 引 言

由于体积庞大、自由度低及灵活性差等缺陷,传统的刚性机器人难以直接投入工业应用[1,2]。

由于独特的灵活性和柔顺性等特点,连续体机器人却非常适用于一些复杂的狭窄非结构化工作环境,如医疗微创手术[3]、飞机油箱检测[4]、核工业管道探测[5]及航空涡轮发动机叶片检测[6]等领域。连续体机器人通常采用类似于章鱼触角、象鼻等具有变形特点的仿生机构,能够通过自身的弯曲变形,适应复杂狭窄、曲折多变的非结构化环境。

多年来,针对于连续体机器人的研究,研究者们大多致力于通过增加结构自由度的方式,以提高机器人系统在受限空间的操作能力[7]。因此,目前在柔性脊柱型结构的研究方面已经取得了较大进展。在这些进展中,比如以超弹性NiTi合金或者具有变形能力的聚合物作为连续体机器人的骨架芯柱,增强了其弯曲能力[8-10];同时,将若干个连接盘沿骨架芯柱方向均匀布局,并采用绳索驱动的方法来实现弯曲变形的功能。但该构型的连续体在弯曲变形时易于产生扭转变形,导致其运动学建模困难和控制精度变差[11]。

LIU S等人[12]在开发有限空间内的灵巧连续机械手过程中,在相邻关节间嵌入了3根弹性支柱,减少了结构的扭转变形;但该研究仍存在关节间耦合性较大,且支撑柱刚度低等缺陷。向立清等人[13]采用了具有双支柱柔性节点的双枢轴柔性关节结构,减少了连续体机器人的扭转变形,有效克服了传统脊柱型连续体机器人的扭曲问题;但其驱动系统仍存在布线复杂、装配困难等问题。

此外,大多学者多采用常曲率圆弧假设原理,进行运动学建模分析[14,15]。HANNAN M W等人[16]提出了一种基于常曲率假设来研究运动学的几何分析法,极大降低了连续体机器人运动建模的难度;但该研究忽略了外部负载导致的芯柱扭转与压缩变形造成的误差。

针对传统绳驱动柔性检测机器人中存在的刚度问题及常曲率建模误差等问题,笔者提出一种基于榫卯结构柔性铰链串联而成的连续体检测机器人,并对该结构进行运动学建模分析与仿真;此外,为实现连续体机器人的运动控制及满足更加直观的人机交互需求,笔者设计一种基于上位机软件及遥控手柄的连续体双层控制系统,通过控制机器人的方式进行样机试验,以对其结构设计与控制策略的有效性进行验证。

1 机械结构设计

为减少驱动绳张力与外部负载对机器人控制精度产生的影响,笔者提出了一种新型的连续体检测机器人,其结构图如图1所示。

图1 柔性检测机器人结构

该系统主要由柔性机械臂、导向张紧单元、绳驱动单元与直线进给单元组成。其中,柔性机械臂由2个弯曲关节串联组成,共有4个自由度,主要实现弯曲作业功能。

笔者设计的连接盘整体呈圆筒状、内部留有圆柱形通道,连接盘间采用十字交叉的榫卯连接。弯曲关节结构示意图如图2所示。

图2 弯曲关节结构示意图

图2中,弯曲单元上部两侧凸起为榫,下部与之成90°交叉的两侧凹槽为卯,装配时将一弯曲单元的榫从侧面推入另一弯曲单元的卯,依次串联形成弯曲关节。榫卯关节通过相对转动提供2个自由度,可保证弯曲关节在等曲率模型下避免中间芯柱的扭曲及轴向压缩变形。

为限制上下弯曲单元的左右攒动,并增加机械臂柔性,笔者将弹簧嵌入到弯曲关节中心通道作为机器人骨架芯柱,从而保证机器人连续变形的同时,以有效避免因过大的局部弯曲角度导致的应力集中与形状不可预测等问题。

弹簧内部为中空,为末端执行器留有布线空间。此外,弯曲关节为模块化设计,可根据需要确定连接盘数量,并进行快速装配。

图2(b)中,在连续体轴向上留有驱动通道,每个关节使用3根驱动绳驱动,每根间隔120°,通过3个独立的无刷直流电机分别控制,从而实现弯曲关节在三维空间中任意变形。相邻驱动绳孔间隔30°,最多可通过4组驱动绳,控制4个弯曲关节的运动。图2(c)为加工的连续体弯曲关节实物。

弯曲关节的结构参数如表1所示。

表1 弯曲关节尺寸参数表

绳索张紧单元每个间隔60°固定在支撑板上,每个单元有2个滑轮组成,用于改变驱动绳的路径,使弯曲单元更近似等曲率圆弧的弯曲变形。动滑轮与压缩弹簧配合,可根据绳索的张力自动改变其压缩量,以保持驱动绳的张紧,有效避免驱动绳在运动过程中出现绳索松弛的情况,防止绳索松弛对弯曲运动所造成的控制误差,及对末端负载造成不利影响。

绳驱动单元由固定在支撑盘上的6个无刷单机和丝杆螺母组成,每3个间隔120°的直线模组控制一个弯曲关节的运动变形,驱动绳一端固定在螺母滑块上,另一端则通过导向张紧单元后,固接在相应弯曲单元的末端连接盘上。

直线进给单元由直线导轨和滑块组成,将机器人系统固定在直线导轨的滑块上,从而实现机器人整体进给运动的目的。

2 运动学分析

为了对柔性机器人进行准确的运动控制,需要精确地描述机器人的运动状态。因此,笔者首先对柔性机器人进行运动学建模[17]。

与传统机器人相比,连续体机器人具有更强的灵活性及超冗余的自由度,因此,对其进行运动学建模相对困难。

为更方便地描述机器人的运动状态,笔者将机器人的工作空间分为3种,即驱动空间、关节空间和操作空间[18]。由于常曲率假说建模过程相对简单,计算效率高,笔者利用常曲率模型假说对柔性机器人进行运动学建模。

2.1 单关节运动学模型分析

为便于运动学模型的分析,笔者构建了单节弯曲单元几何模型,如图3所示。

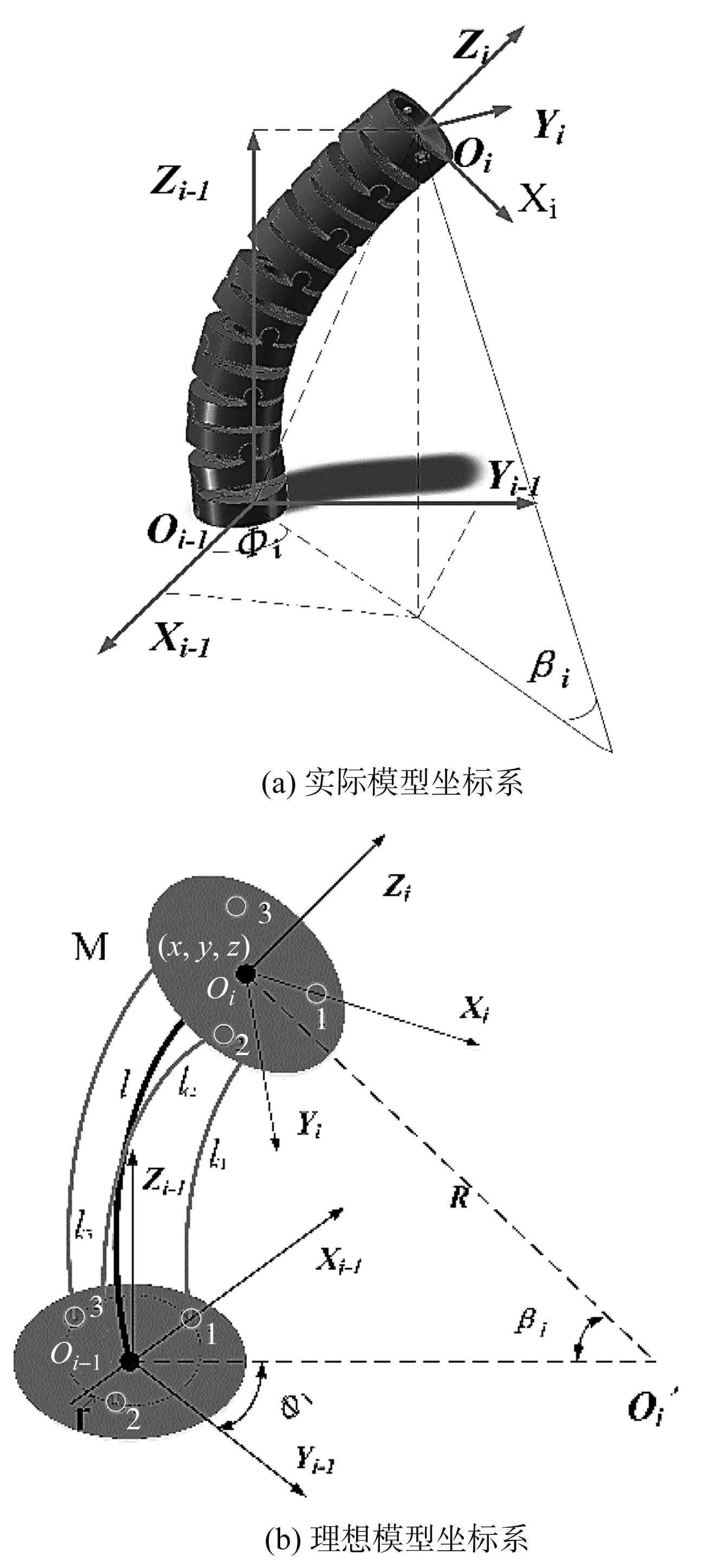
图3 单关节连续体段坐标及关节变量定义

图3(a)中,坐标系{Oi-1}的原点与基座圆盘中心重合,坐标系{Oi}的原点与末端导线圆盘中心重合,Zi和Zi-1方向为芯柱弹簧等效杆的切线方向,Xi-1和Xi指向导线圆盘第一个驱动丝通孔的方向。

为便于分析,笔者将其简化为如图3(b)所示的等曲率连续光滑曲线。为描述单节弯曲单元前后端坐标系间的相互关系,定义了3个变量参数:单关节的芯柱长度L;弯曲角度为圆弧的圆心角记为βi;旋转角度为平面OiOi-1Oi,和平面YOZ的夹角记为Φi。

对于等曲率弯曲模型[19],弯曲单元中心线圆弧对应的半径为R,则弧长与半径的关系如下式所示:

(1)

假设弯曲末端中心点为M(x,y,z),则点M的坐标如下式所示:

(2)

2.1.1 关节空间与工作空间的映射

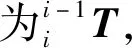
(1)将坐标系Oi-1沿着自身坐标轴Z轴旋转Φi,如下式所示:

(3)

(2)将原点Oi-1沿弧线平移到原点Oi处,如下式所示:

(4)

(3)沿着自身坐标轴Y轴逆时针旋转βi,如下式所示:

(5)

(4)将其沿自身Z轴旋转-Φi,如下式所示:

(6)

通过四次变换,可得到第i-1段到第i段弯曲单元的其次变换矩阵,如下式所示:

(7)

式中:c—余弦函数的缩写;s—正弦函数的缩写;Φi∈[0,2π],βi∈[0,π/2);l—弯曲关节整体长度。

各个关节均为常曲率模型,依此类推,第n个弯曲关节到第1个弯曲关节之间的坐标系齐次变换矩阵,可由各弯曲单元的变换矩阵累乘求得,如下式所示:

(8)

通过上述分析,笔者对连续体的单弯曲关节进行正运动学建模,并得到工作空间与关节空间的映射。

接下来对连续体机器人的单弯曲关节进行逆运动学分析。

由式(1,2)可得弯曲关节末端位置M(xi,yi,,zi)的关节空间变量表达式,即:

(9)

由式(9)可求出圆弧的圆心角(弯曲角度),记为βi,平面OiOi-1Oi′和平面YOZ的夹角(旋转角度),记为Φi,如下所示:

(10)

2.1.2 关节空间-驱动空间的映射

与传统串联机器人相比,绳驱动连续体机器人每个关节的变化受到穿过后端弯曲关节驱动绳长变化的影响,因此,为了更好地对连续体机器人进行控制,需建立关节空间与驱动空间(绳长空间)之间的映射关系。

在连续体机械臂弯曲的过程中,根据常曲率假设建模条件可知:在理想状态下,假设驱动绳和芯柱弹簧都是等曲率的,弯曲半径之间有一个差值,其几何示意图如图4所示。

图4 连续体机器人驱动绳模型

图4中,r表示驱动绳分布的分度圆半径。

由几何关系可以推算出Ri1、Ri2、Ri3的表达式为:

(11)

由此,可推出驱动空间与关节空间的映射关系,即:

(12)

2.2 工作空间与驱动空间仿真分析

根据上述运动学模型可知,连续体机器人与传统工业机器人的工作空间数学表达式不同,因而难以用分析法求解机器人的工作空间,所以,笔者在此处采用蒙特卡罗法来求解机器人的工作空间。

由表1可知其单关节长度为196 mm,外单个关节弯曲角度βi∈[0,90°],关节旋转角度Φi∈[0,360°]。笔者分别进行单关节及双关节的工作空间仿真,工作空间点云图如图5所示。

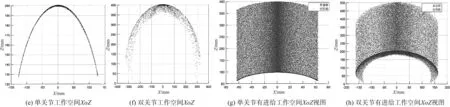
图5 连续型机器人工作空间仿真图

根据图5(a,b)可知:连续体机器人的工作空间为一个开口的中空球体,随着关节的增加,其可达空间越来越大;

如图5(c,d)中,为进一步扩大连续体机器人的工作空间,笔者将连续体检测机器人安装在直线导轨上,提供一个推送自由度,设定推送单元的长度为200 mm。

由于连续体机器人工作空间的对称性,笔者对其工作空间在XOZ平面的剖视图进行分析,仿真结果分别如图5(e～h)所示;并且由单双关节的对比看出,随着关节数的增加,弯曲关节的盲区越来越小。

为控制连续体机器人的弯曲变形,根据前述关节的运动学算法,笔者需对关节运动时驱动绳的长度变化进行仿真,其仿真结果如图6所示。

图6 双节弯曲单元弯曲绳长变化图

笔者设置关节初始状态弯曲角度为β1=2π/3,然后将关节1,即靠近基座的关节(#1关节)与关节2(#2关节)的扭转角Φi定义在[0～2π]内,进行关节扭转和绳长变化之间关系的仿真。

当两组关节协同运动时,#2关节会受到#1关节弯曲运动的影响。#1关节静止,#2关节的驱动绳只受#2关节本身弯曲影响,如图6(a)所示;

#1关节发生弯曲,#2关节保持不动,#2关节的3根驱动绳会因为耦合,随#1关节的驱动绳变化而变化,如图6(b)所示;

在机器人实现类S形姿态时,驱动绳的绳长变化轨迹表明,其末端关节的绳索总长变化量受前面通过的关节变化影响,如图6(c)所示。

3 控制方法研究

为更好地实现人机活动,提高控制的精度,笔者搭建了连续体机器人的控制系统,其控制方案如图7所示。

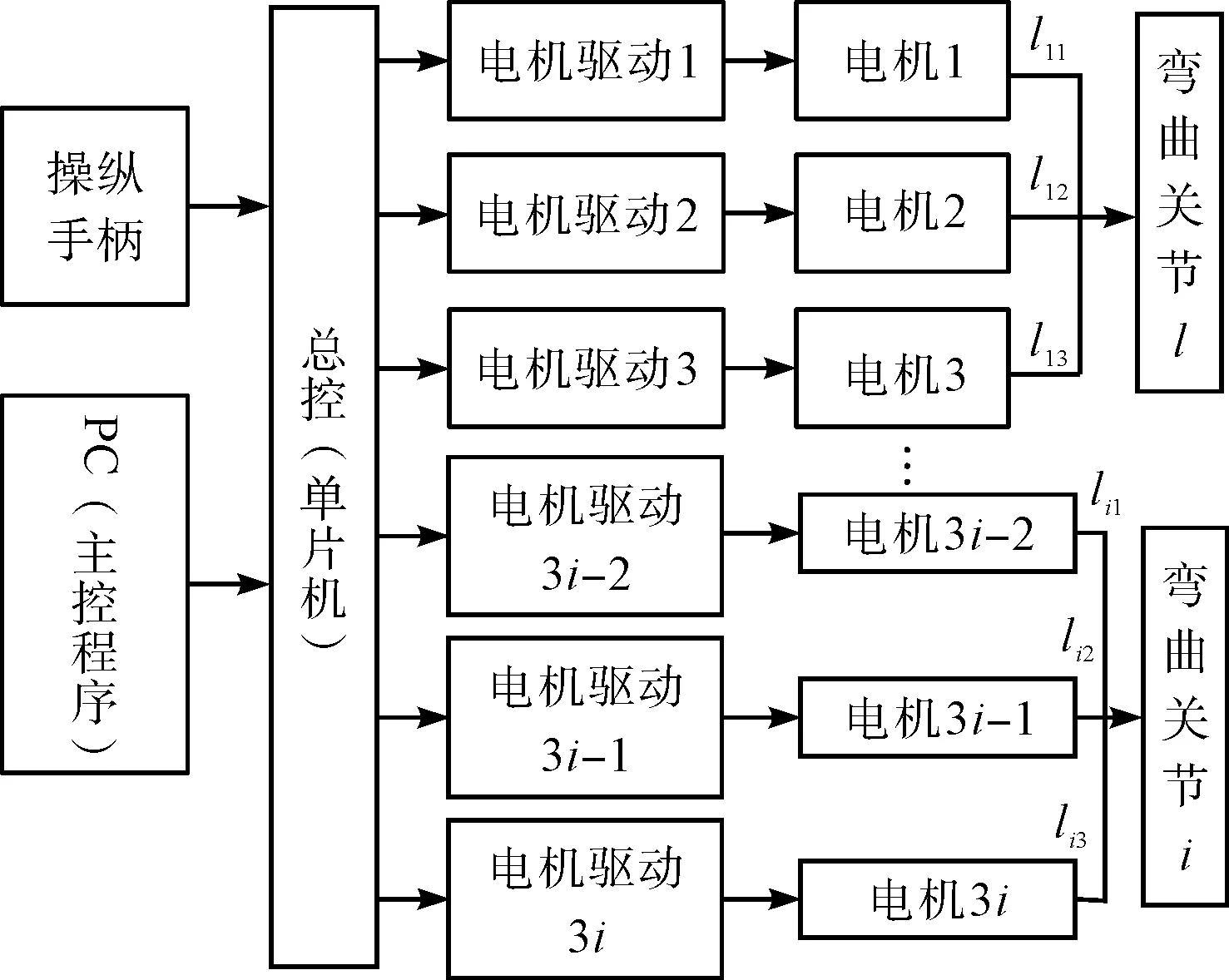
图7 连续体机器人控制方案框图

连续体机器人操控系统由上位机、遥控手柄以及驱动板组成,由上位机与遥控手柄协同控制驱动电机,操作员可通过上位机发出指令,控制电机驱动弯曲关节至目标点,或通过操纵遥控手柄调节末端关节位姿。

连续体机器人操作流程如图8所示。

图8 连续体机器人操作流程图

基于遥控手柄的主动控制过程如下:

主手遥控手柄采用joystick摇杆,输出两路模拟量信号。为了便于计算,用单片机将模拟量简化为数字量(0～256),并取摇杆中心为数字量中点,建立直角坐标系,则X,Y轴的取值范围为(-127,127)。

由于连续体机器人的关节空间涉及角度,笔者将手柄的直角坐标系转化为极坐标系,并取α、r为极坐标系两自变量。

为了将操作手柄与弯曲关节的末端对应起来,笔者采用基于关节空间的增量映射模型,按照一定的比例,将操纵手柄在极坐标系中α、r的坐标增量映射到连续体末端机械臂的构型空间(β,Φ)。

基于关节空间的增量映射如图9所示。

图9 基于关节空间的增量映射

转换关系如下式所示:

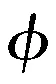
(13)

式中:K1，K2—捻转角度与弯曲角度的比例系数,经过多次校准试验计算得出K1=1,K2=0.017 5。

为了实现基于上位机的控制策略,笔者编写了柔性检测机器人的人机交互控制界面,如图10所示。

图10 上位机操作界面

当操作员在上位机输入2个弯曲关节的弯曲角与偏转角时,上位机经过计算生成命令,实现连续型机器人的自动控制的目的,并根据运动学模型生成理想曲线;

此外,窗口可直观显示测量曲线(由采集的关节姿态信息生成)。

4 试验测试

为了验证新构型的弯曲关节运动学模型的有效性与双层控制策略的准确性,笔者搭建了试验平台,并设计了一系列试验进行验证。

试验平台如图11所示。

图11 试验平台

试验平台由PC、总控板、移动电源、无刷直流电机、电机驱动板、直线导轨与弯曲关节等组成。笔者只对一节弯曲关节(末端关节)进行试验与结果分析(进行单关节的旋转试验、主从控制试验与负载弯曲试验),由坐标系得到弯曲关节的姿态。

4.1 单关节旋转试验

由于机器人弯曲单元在任一弯曲平面内具有各向同性,弯曲角度为0°～90°,旋转角为0°～360°,故笔者该仅对弯曲角度为90°情况下试验结果进行分析,即当弯曲角90°时(弯曲极限),将旋转角在0～360°范围内间隔45°取值,进行平面旋转试验,以验证弯曲关节的可达范围。

机器人的运动过程,即弯曲关节旋转试验如图12所示。

图12 弯曲关节旋转试验

试验结果表明:弯曲关节具有较好的柔韧性,且常曲率运动模型适用于解算上述连续体机器人的姿态。

4.2 末端关节主从控制试验

为了验证双层控制的准确性与可行性,笔者在上位机与操纵手柄控制下,进行连续体机器人末端关节(单关节)弯曲试验。

试验步骤如下:

(1)在上位机界面输入第一关节弯曲角度为30°,旋转角度为0°,测量此时的实际弯曲角度,并加以标记;

(2)通过操纵遥控手柄的方式操作末端位姿,并标记此时的弯曲角度;

(3)依次按照上述步骤操控弯曲关节至[0°,60°]、[180°,30°]等位置,得到主从控制试验结果,如图13所示。

图13 主从控制试验结果

由图13可知:两种操作模式均可以对弯曲关节进行有效控制,虽然实际弯曲角度与理想弯曲角度均存在误差,但是误差仍在可接受范围之内;

在旋转角为0°时,实际弯曲角会因重力作用比理想状态多向下弯曲;当旋转角为180°时,向上弯曲,实际位姿会因为重力作用反而略小于理想弯曲角。

由上述试验可知:基于常曲率模型的解算适用于此处的的弯曲关节;该双层控制策略的可行性和有效性得到了验证;误差是弯曲关节的连接盘自身重力影响导致的。

4.3 负载弯曲试验

上文已经验证了控制方法的有效性,通过上位机控制方式,笔者进行连续体机器人的负载弯曲试验。

对其进行初始化后,笔者将连续体机器人的弯曲角与旋转角恢复为0°;并分别在末端关节施加50 g、150 g、250 g的砝码情况下,控制末端关节分别弯曲30°与45°,则可得到实际位姿图,如图14所示(虚像与实像分别为30°与45°时的实际位姿)。

图14 刚度试验

笔者每次改变弯曲角15°,并测量(采用三维坐标系)末端弯曲关节的实际位置,即测量末端中心点在基座系的位置M1(X1,Y1,Z1),每组测量10次取平均值,并将其与理论位置M0(X0,Y0,Z0)进行误差计算。

误差公式如下:

(14)

笔者记录每组弯曲角度在不同负载下的位姿误差,生成位姿态偏差图,如图15所示。

图15 位姿误差图

由图15可知:随着负载的增加,连续体的位置误差增大,控制精度降低;但最大负载250 g时的位置误差小于8%,仍在控制许可范围内。

结果表明:该弯曲关节具有较高的刚度,可以承担较大的负载需求;在弯曲角度较小时,由于驱动绳没有完全张紧,并且弯曲关节水平放置受重力影响较大,故位置误差在启动时误差较大;随着弯曲角度的增大,误差虽然会因为累积增大,但误差增加不明显,并且逐渐趋于稳定。

5 结束语

笔者设计了一种基于十字交叉榫卯连接的弯曲关节,根据常曲率假设,建立了机器人运动学模型,运用MATLAB软件对连续体机器人进行了运动学分析,并提出了双层控制策略,最后通过样机系统进行了试验验证。

研究结果表明:

(1)与传统工业机器人相比,笔者设计的弯柔性机械臂可达工作空间更广泛,可以实现360°的旋转运动,最大弯曲角度可达90°,并且位置的误差波动较小;

(2)笔者提出的控制策略能对机器人进行行有效控制,利用双层控制策略,可以更加快捷地实现人机交互的目的,并有效调节机械臂的末端位置;

(3)单关节柔性机械臂在250 g负载下的位姿误差小于8%,具有较好的刚度与负载能力。

笔者所设计的柔性机械臂可达工作范围大、负载能力强、控制精度高,达到了预期设计目的,为柔性机器人的刚度问题提供了可行方案。

在后续的工作中,笔者将针对该柔性机械臂的具体结构,研究其特定的运动学模型算法,并对手柄的主从控制策略进行进一步的优化。