基于S-CBiGRU的风电机组滚动轴承故障诊断方法*
史宗辉,陈长征,2*,田 淼,安文杰,孙鲜明
(1.沈阳工业大学 机械工程学院,辽宁 沈阳 110870;2.振动噪声控制工程技术研究中心,辽宁 沈阳 110870;3.宁波坤博测控科技有限公司,浙江 宁波 315200)
0 引 言
由于大多数风电机组都被安装在沙漠、戈壁等恶劣的环境中,且机组长期受到风力冲击[1]和交变载荷的影响,导致作为风电机组重要零部件的滚动轴承极易遭到损坏。因此,对滚动轴承进行故障诊断,以保证风电机组良好运行,具有重要的意义。
目前,针对风电机组滚动轴承故障诊断的信号来源,主要以振动信号为主[2,3]。风场采集到的振动信号存在非线性、非平稳的特性。
时频分析是一种处理非线性、非平稳信号的有效方法。时频分析的方法主要有短时傅里叶变换(short time Fourier transform,STFT)、连续小波变换(continuous wavelet transform,CWT)与S变换(S-transform)等。
CHEN Jun-gan等人[4]在采用时频分析方法进行故障诊断时,考虑了STFT的窗口大小与振动信号频率之间的关系,因而提高了时频分析方法的通用性。TRAN M Q等人[5]在进行故障诊断时,利用连续小波变换(CWT)方法,将振动信号转化为尺度图特征图像,提高了故障诊断效果。
运用上述方法对振动信号进行时频分析时,由于STFT存在窗口大小无法随着频率改变的问题,而CWT存在小波基函数选取困难的问题,笔者选取STFT与CWT融合改进的S变换的时频分析方法,利用高斯窗函数替代CWT中小波基函数,同时窗宽可变,可以有效解决上述问题。
近年来,在复杂装备故障诊断领域中,采用深度学习方法的表现优异[6,7]。O’SHEA T J等人[8]提出了一种用于调制类型分类的卷积神经网络(convolutional neural network,CNN),并对该网络进行了实验验证,结果表明,CNN的鲁棒性更强。GAO Shu-zhi等人[9]利用改进CNN,对滚动轴承进行了故障诊断,结果表明,该方法可以提高其网络收敛性。
然而,利用CNN进行故障诊断时,对时间的依赖性不高,无法捕捉振动信号时域的依赖关系。
循环神经网络(recurrent neural network,RNN)是一种善于捕捉信号间时间依赖关系的方法,常被用于有时间序列信号的分析。常见的RNN有长短时记忆网络(long short-term memory,LSTM)、门控循环单元网络(gated recurrent unit,GRU)[10,11]。
在对剩余使用寿命进行预测时,为了降低预测的误差,HSU C Y等人[12]利用改进的LSTM分析了特征之间的时间依赖关系。GRU结构作为LSTM结构的变体之一,虽然网络结构参数少,但在一定程度上可提高计算效率。TAO Ying等人[13]利用三层GRU结构逐层深入学习了故障特征,实现了齿轮箱故障诊断的目的。
但上述方法仅能提取信号中t时刻及其前一时刻信号特征,无法提取t时刻之后的有用特征。振动信号为时间序列数据,t时刻及其前后时刻都包含有用特征。因此,笔者提出用BiGRU方法来提取信号中t时刻及其前后时刻的特征,使特征提取更全面。
针对以上问题,笔者提出一种基于S变换、卷积神经网络(CNN)、双向门控循环单元(BiGRU)的故障诊断方法,即基于S-CBiGRU的方法。
首先,利用S变换对振动信号进行时频分析,生成时频图;其次,将其输入到搭建的CBiGRU网络模型中,利用CNN卷积池化层提取时频图的空间特征;随后利用BiGRU提取时间正序与逆序中的时间特征(多角度提取故障特征);最终,实现风电机组滚动轴承故障诊断的目的。
1 基本原理
1.1 S变换
S变换[14]是一种优异的时频分析方法。它利用可伸缩的高斯窗与连续小波变换的相位矫正,对信号进行多分辨率的分析。
振动信号x(t)的S变换为:
(1)
式中:t—时间;τ—控制窗口函数在时间轴上的位置;f—频率;ω—高斯窗函数。
高斯窗函数ω(τ-t,f)可表示为:
(2)
由式(1,2)可得到连续振动信号S变换为:
(3)
由于要构造S变换时频特性复矩阵,因此需将S变换离散化,振动信号x(t)可离散为x(kT),T为采样间隔,将离散采样信号的傅里叶变换为:
(4)
其中:n=0,1,…,N-1,N为采样点数。
令τ→kT,f→n/NT,因此离散S变换为:
(5)

S变换利用高斯窗函数,避免了STFT时频窗不变的缺点,同时改善了CWT局部相位不变的缺点。因此,S变换在时域、频域都可以获得高分辨率,时频分析的效果更显著。
1.2 卷积神经网络
卷积神经网络(CNN)作为一种近年来发展迅速的前馈神经网络,常被用于轴承的故障诊断[15]。
CNN由输入层、卷积层、池化层、全连接层、输出层组成,其结构如图1所示。
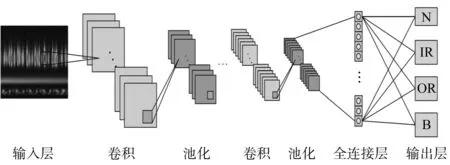
图1 CNN结构图
卷积层的作用为特征提取,将输入层中的数据与卷积核进行卷积运算,其表达式为:
(6)

为防止过拟合,笔者在每一个卷积层后接一个池化层。
采用最大池化的方式减小神经网络中参数为:
(7)
式中:A—池化区域宽度。
1.3 BiGRU网络
在误差反向传播的过程中,循环神经网络(RNN)[16]会出现梯度消失现象。为了解决梯度消失问题,通常采用其变体结构LSTM与GRU。
GRU网络结构如图2所示。
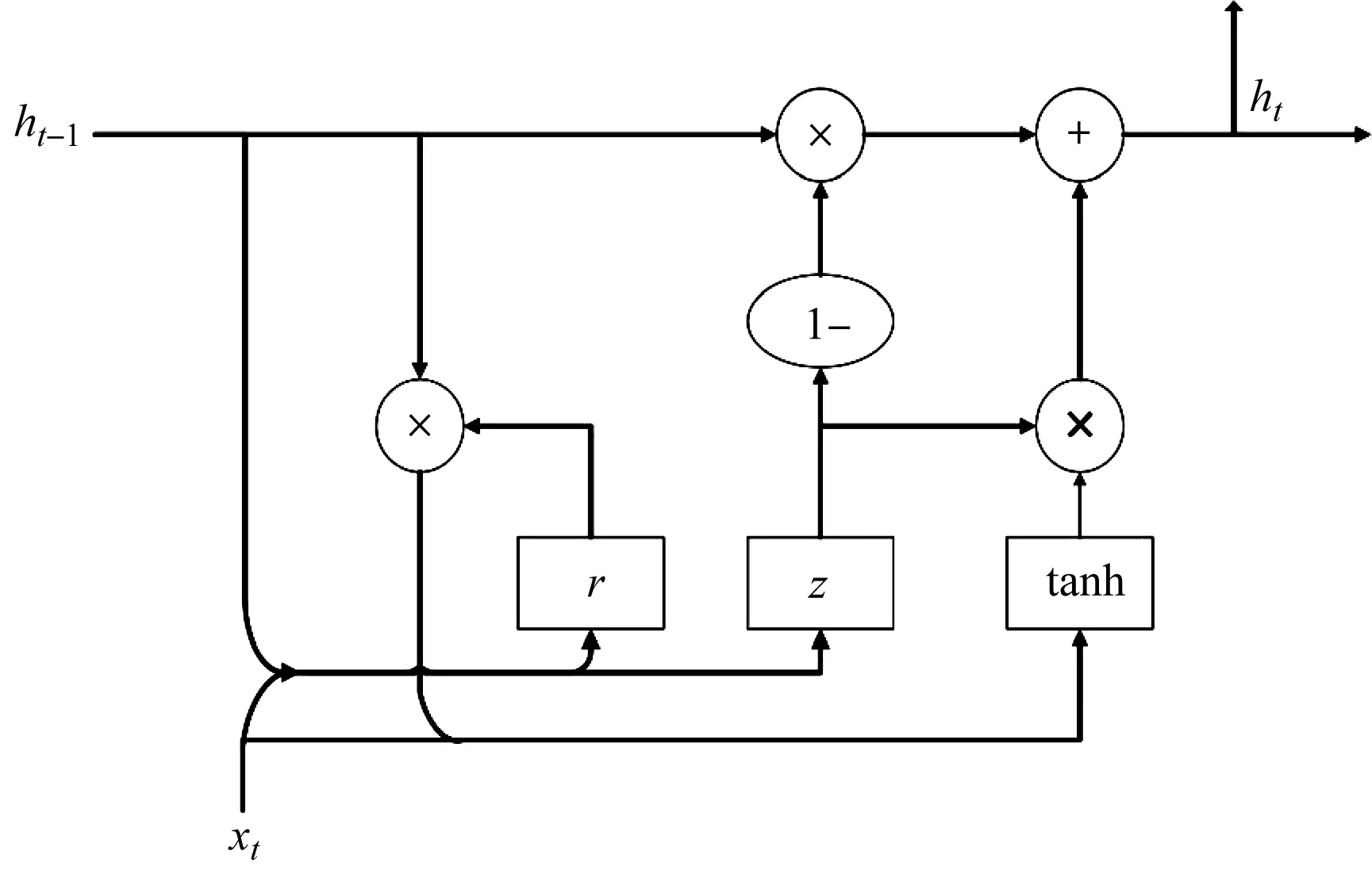
图2 GRU网络结构图
与LSTM相比,GRU只有更新门zt与重置门rt(t为当前时刻)。
相关计算公式为:
rt=σ[Wr⊗(ht-1,xt)]
(8)
zt=σ[Wz⊗(ht-1,xt)]
(9)
(10)
(11)
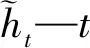
振动信号是时间序列数据,当轴承发生故障时,t时刻及其前后都包含着故障信息。GRU网络只能提取t时刻及其前一时刻信息,无法获取t时刻之后的信息,因此,为了解决上述问题,笔者在此处引入BiGRU。
BiGRU由两列GRU组成,按照时间正序与逆序对振动信号进行特征提取。
BiGRU模型结构如图3所示。
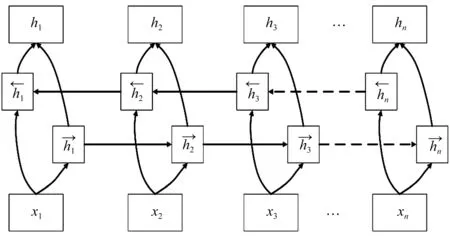
图3 BiGRU模型结构图

(12)
(13)
(14)
式中:GRU(·)—GRU单元;T(·)—t时刻隐藏状态输出。
2 故障诊断流程
振动数据经S变换后得到其时频图,CNN卷积池化层提取时频图中的空间特征信息,BiGRU从时间正序、逆序中捕获时间特征,多角度提取特征。
CBiGRU结构如图4所示。

图4 CBiGRU结构图
基于S-CBiGRU的风电机组轴承故障诊断步骤如下:
(1)利用风场采集振动信号,采用S变换进行时频分析,生成时频图,划分训练集与测试集;
(2)构建CBiGRU网络,调整网络参数,利用训练集数据训练CBiGRU模型;
(3)以测试集为输入,利用S-CBiGRU模型进行故障诊断,最终得出故障诊断结果。
风电机组滚动轴承故障诊断流程图如图5所示。

图5 风电机组滚动轴承故障诊断流程图
3 实验及结果分析
3.1 实验
为了对上述轴承故障诊断方法的有效性进行验证,笔者进行了实验,并将实验数据输入到该模型中,进行验证。
实验振动数据来源于内蒙古锡林浩特某风场,轴承测点位置为风电机组发电机驱动端径向,传感器为ICP压电加速度传感器,采样时间20 s,采样频率16 384 Hz。
在数据集中,滚动轴承状态由正常状态、内圈故障、外圈故障、滚动体故障4种状态组成。
振动信号采集如图6所示。

图6 振动信号采集图
滚动轴承的数据集如表1所示。
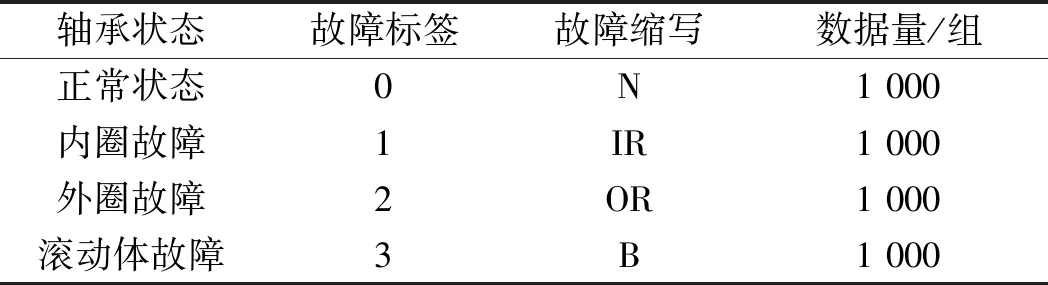
表1 滚动轴承数据集
表1中,0,1,2,3分别代表滚动轴承正常状态、内圈故障、外圈故障、滚动体故障4种状态。
3.2 结果分析
由风场采集的风电机组滚动轴承振动信号时域图如图7所示。

图7 滚动轴承振动信号时域图
图7中,包含有滚动轴承4种状态,即正常状态、内圈故障、外圈故障和滚动体故障。由于振动信号具有非线性、非平稳的特性,笔者对振动信号进行时频分析;又因STFT窗函数无法改变,CWT小波基选取困难的问题,所以笔者选取S变换进行时频分析。
由S变换后的滚动轴承4种状态的时频图如图8所示。

图8 滚动轴承振动信号时频图
由S变换生成的时频图,每种状态生成1 000组数据,随机选取80%组作为训练集;将划分后的训练集时频图谱输入到CBiGRU模型中进行训练。
CBiGRU网络模型参数如表2所示。

表2 CBiGRU网络模型参数
CBiGRU模型输入为S变换后的时频图,利用卷积池化层提取时频图中的空间特征,BiGRU层提取时间正序、逆序特征,以便从时频图中获得更多故障信息,最后由SoftMax层对滚动轴承故障进行分类。
在CBiGRU模型中,模型学习率设置为0.001,batch size为32,为防止网络发生过拟合,在全连接层中引入Dropout层并设置为0.5。
笔者选取交叉熵损失函数为网络模型的损失函数,网络的故障分类准确率如图9所示。

图9 CBiGRU网络故障分类准确率
网络的损失值图10所示。

图10 CBiGRU网络损失值
由图(8~10)可知:利用S-CBiGRU网络进行滚动轴承故障诊断,训练集的准确率达到93.81%,损失值为0.06;当迭代30次后,故障准确率曲线与损失曲线都趋于平稳,模型收敛。
笔者通过对测试集样本的分类,绘制混淆矩阵,如图11所示。

图11 混淆矩阵
在图11中,横轴表示预测类别,纵轴表示实际类别,数字“23”代表23个外圈故障(实际故障为滚动体故障,被网络错误划分为外圈故障)。由混淆矩阵可知:S-CBiGRU网络可以有效区分出滚动轴承的不同故障。
为验证S-CBiGRU采用S变换的优越性,笔者将其与两种常用的时频分析方法STFT与CWT进行对比实验。
同一组振动信号,采用S变换、STFT、CWT分别进行时频分析,得出时频图谱后,再将其输入到CBiGRU网络中,对其进行故障分类。
故障分类准确率如图12所示。

图12 故障分类准确率
由图12可知:在上述3种时频分析方法中,利用S变换进行时频分析的准确率最高,达到93.17%;
由于S变换窗口大小可变,在高频时段,窗口较窄,时间分辨率高;在低频时段,窗口较宽,频率分辨率高;
在多分辨分析中,可以获得信号中更多的信息。因此,与STFT、CWT方法相比,采用S变换得到的故障识别准确率更高。
深度学习常被用于滚动轴承的故障诊断,常用的深度学习方法有:AlexNet、VGG16、GRU等。为了证明S-CBiGRU网络的故障分类能力的优越性,笔者将其与其他深度学习方法进行对比实验。
笔者采用不同算法得到的故障分类准确率,如图13所示。

图13 不同算法故障分类准确率
由图13可知:振动信号以S变换后的时频图作为输入,采用AlexNet、VGG16、GRU及CBiGRU模型进行故障分类,S-CBiGRU模型分类准确率最高,达到93.17%;
由于S-GRU与S-CBiGRU考虑振动信号为时间序列,提取t时刻及其前一时刻的故障特征进行故障诊断,所以准确率高于AlexNet、VGG16模型的准确率;
由于S-CBiGRU不仅考虑时间正序,还考虑时间逆序,即提取t时刻及其前后时刻的故障特征,获取的故障特征更全面。因此,利用S-CBiGRU模型进行风电机组滚动轴承故障分类效果优于其他深度学习算法。
4 结束语
针对风电机组滚动轴承的振动信号存在非线性、非平稳特性,且特征不易提取的问题,笔者提出了一种基于S-CBiGRU的故障诊断方法,利用风场采集的振动信号进行了故障诊断。
研究结论如下:
(1)利用了S变换解决振动信号的非线性、非平稳问题,并生成了二维时频图作为模型输入,在CNN中引入了BiGRU结构,构建了CBiGRU网络模型,由CNN卷积池化层与BiGRU层分别提取了二维时频图中信号的空间特征与时间正序和逆序特征,深度挖掘了信号中所包含的故障特征,最终实现了滚动轴承故障诊断的目的;采用风机实际数据诊断的准确率高达93.17%;
(2)不同深度学习方法的对比实验结果表明,基于S-CBiGRU的故障诊断方法提取的信号特征更全面,并可解决信号的非线性、非平稳问题,诊断效果优于传统深度学习方法,可以为风电机组滚动轴承故障诊断提供理论基础。
在今后的相关工作中,笔者将继续对风力发电机组故障诊断进行深入研究,并结合机组的振动参数及其它参数,对其故障进行融合诊断。

