基于多表示动态自适应的不同工况下滚动轴承故障诊断*

朱继扬,孙虎儿,张天源,赵 扬,白晓艺

(中北大学 机械工程学院,山西 太原 030051)

0 引 言

滚动轴承是机械系统的重要零部件,其是否能健康运行对机械系统的平稳运行具有重大的影响,故对其开展故障诊断和状态监测意义重大。

随着深度学习的不断发展,基于深度学习的轴承智能故障诊断方法得到了广泛应用,并且已经取得不少的成果[1,2]。在深度学习的实际应用中,因为机械设备工作条件的改变,故障样本的分布特征往往会发生变化;并且对于每个不同工况,几乎不可能收集到足够多的标记故障样本,这极大地限制了基于深度学习的故障诊断的泛化能力。

迁移学习是一种挖掘不同数据分布之间相似性的方法,它可以将源域中的知识转移到目标域中[3]。

域适应是迁移学习中的一个重要概念[4]。域适应的主要目的是,通过比对源域数据和目标域数据的特征分布,尽可能多地学习源域中带标签数据的隐藏信息,帮助完成目标域中的任务[5,6]。

LI Xiang等人[7]提出了一种基于自编码器网络的深度域自适应方法,实现了跨机迁移学习的故障诊断目的。HAN Te等人[8]将边缘分布适应扩展到联合分布适应,该方法能有效地利用源域中有标记的数据,对无标记的目标域进行迁移学习故障诊断。SHAO Jia-jie等人[9]利用了短时傅里叶变换,将原始数据转换为时频图像,采用最大平均差异和域混淆函数对其进行了域自适应,提取了两个域之间的域不变特征,实现了跨域故障诊断目的。LIAO Yi-xiao等人[10]利用实例加权动态最大平均偏差进行了动态分布适应,并且进一步衡量了每个类别条件分布的所占比例,而且考虑目标域中软伪标签的置信度,将源域和目标域的迁移特征进行了对齐。SHEN Chang-qing等人[11]提出了一种动态联合分布对齐网络,以此来动态定量地评估边缘分布和条件分布的相对重要性,同时使用软伪标签更准确地度量了不同域之间的条件分布差异。

但是以上这些方法都是根据单个结构进行表示分布特征提取,而该特征分布只包含部分信息。

大多数滚动轴承数据都是一维时间序列或频率序列。与直接使用原始的一维数据相比,将原始的一维数据转换为二维数据,可能会导致故障诊断的效果较差[12]。如何利用一维卷积神经网络提取一维振动信号,进行迁移学习故障诊断是近年来业界的研究的热点。

WANG Kai等人[13]提出了一维多尺度域自适应网络,采用了特征自适应和分类器自适应两种方法,以此来指导多尺度卷积神经网络对不同工况下的轴承故障进行诊断。HUO Chun-ran等人[14]提出了一种改进的自适应维数转换卷积神经网络,通过该网络,自适应地将一维振动信号转化为二维矩阵特征,并采用分层交替迁移学习方法,对模型进行训练。WANG Zhi-jian等人[15]建立了一种可对原始数据进行故障诊断的模型,即子域自适应迁移学习网络,并提出了边缘分布和条件分布偏差,以及网络层之间的贡献程度。ZHANG Rui-xin等人[16]使用一维轻量级卷积神经网络,从原始振动信号中快速提取了其高级特征,采用了LMMD拟合源域和目标域数据的概率分布,实现了故障分类目的。JIN Tong-tong等人[17]提出了一种多层自适应卷积神经网络,并以原始时间信号为输入,将自适应归一化批处理和多核最大均值差异相结合,提高了模型的域适应能力。LV Ming-zhu等人[18]提取了原始振动数据的可转移特征,然后构造了加权混合核函数,将不同的可转移特征映射到统一的特征空间,并动态评估了边缘分布和条件分布的相对重要性;但是由于基于一维卷积神经迁移网络过于复杂,模型层数很高,参数很多,造成了模型整体性能较差。

为了解决上述问题,笔者以原始振动信号作为神经网络的输入,通过多表示动态自适应(MRAN)算法多表示对齐可迁移的特征、自适应动态的衡量边缘分布和条件分布相对重要性,从而构建一种新的深度迁移模型,即一维多表示空洞动态自适应迁移网络(1D MRDDATN),并在CWRU的滚动轴承数据集进行实验验证。

1 理论背景

1.1 问题描述

源域样本个数为ns,目标域样本个数为nt。源域与目标域的特征空间相等即xs=xt,种类相等即ys=yt。

设源域数据的分布为Ps(xs),目标域数据的分布为Pt(xt),但Ps(xs)≠Pt(xt),笔者提出一种深度自适应网络,使源域的故障诊断知识能够运用到目标域中,实现对目标域的故障诊断。

1.2 动态分布自适应

动态分布自适应(DDA)[19]2能够定量地评估每个分布的相对重要性,并且很容易地融入到结构风险最小化的框架中,以解决迁移学习的问题。

距离度量准则用于度量不同域间数据分布的差异,在迁移学习中起着重要作用。一般来说,MMD[20]通常用来测量不同数据之间的分布差值,它可以有效地测量两个不同分布特征在可再生核希尔伯特空间中的距离。

边缘分布的MMD距离如下:

(1)

式中:Ds—源域的样本;Dt—目标域中的样本。

条件分布的CMMD距离如下:

CMMD(Ds,Dt)=

(2)

为了更好地实现源域和目标域数据分布的动态适应性,笔者利用分布权重因子μ来动态调整两个分布之间的距离,形成了动态分布距离(dynamically distributed distance,DDD),DDD的表达式如下:

DDD=(1-μ)MMDMarginal(Ds,Dt)+μWCMMD(Ds,Dt)

(3)

式中:μ∈[0,1],μ接近1时,说明源域与目标域的数据条件分布差异明显;当μ接近0时,说明源域与目标域的数据边缘分布差异明显。

dM(Ds,Dt)=2(1-2ε(k))

(4)

式中:ε(k)—线性分类器在源域和目标域数据之间的误差。

用dc来表示对应于类别c的条件分布距离,即:

dC(Dsc,Dtc)=2(1-2ε(k)c)

(5)

式中:Dsc—源域的第c类的样本;Dtc—目标域的第c类的样本。

最终,μ的表达式为:

(6)

最终,DDD的表达式为:

(7)

2 1D MRDDATN网络结构

2.1 1D MRDCNN

在深层神经网络中,为了增加感受野,且降低计算量,总要进行降采样(pooling或conv)处理。降采样后,虽然增加了感受野,但空间分辨率也降低了。

为了不丢失分辨率,又能扩大感受野,可以使用空洞卷积。一方面增大感受野,可以检测较大的特征目标;另一方面提高分辨率,可以精确定位目标。

为了更全面地表示原始数据,可以通过多表示的方法进行多种特征提取。通过不同卷积核卷积可以观察到多种不同的特征,从而实现多表示的方法。

根据空洞卷积和多表示的思想,笔者提出了一维多表示空洞卷积神经网络(1D MRDCNN)。该网络在低层特征中,使用卷积核较大的空洞卷积,然后采用CONCAT操作,融合不同大小卷积核所提取的特征;在高层特征中融合不同的较小卷积核卷积的特征,这样可以更好地提取并区分不同类别数据的特征,增加网络的特征表达能力。

1D MRDCNN的总体结构如图1所示。

图1 1D MRDCNN网络结构

网络结构参数如表1所示。

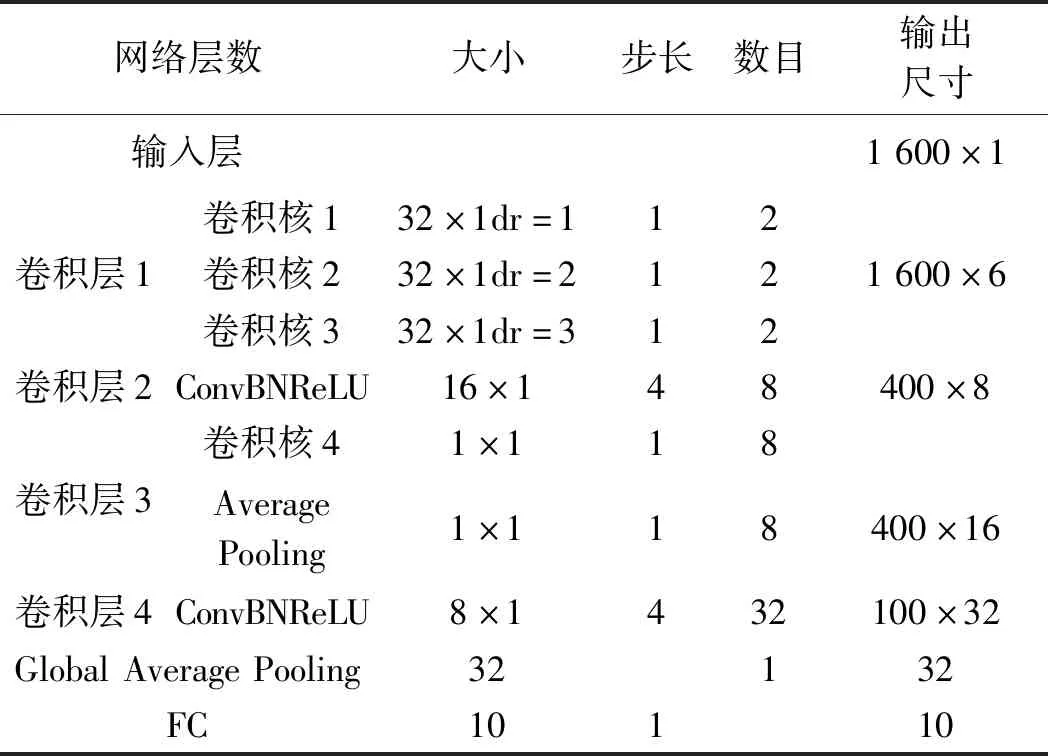
表1 1D MRDCNN网络结构参数

1D MRDCNN由4个卷积层、1个全局平均池化层和1个全连接层组成。网络模型的层数为6,总参数为5 664,可训练的参数为5 584,不训练的参数为80,为简单轻量级的网络模型。空洞卷积中的dilation rate为在卷积核中填充dilation rate-1个0(表1中的dr为dilation rate)。

2.2 MRDA

一些最新的深度迁移学习方法使用全局平均池化层的激活作为特征表示,然后对齐单个表示的分布。但是,只在单一结构上做特征对齐也只能关注到部分信息。

由于不同的结构可以从特征中提取出不同的表示,笔者使用多个子结构,结合DDA方法和多表示自适应(MRA)[21]4方法,构成多表示动态自适应结构(MRDAM)。MRDAM替换了1D MRDCNN的全局平均池化层形成了1D MRDDATN。

1D MRDDATN网络结构如图2所示。

图2 1D MRDDATN网络结构

MRDAM有3个各不相同的子结构,且每个子结构上的边缘分布、条件分布、μ都不一样。分类器包含一个全连接层和一个SoftMax层,全连接层主要用于对多个表示进行重组,SoftMax层用于输出预测标签;

MRDAM是一个多表示动态特征提取器,与单一表示相比,多表示可以涵盖更多的信息,而且可以将每个表示进行动态分布对齐;最小化多表示的分布差异,以便获得更好的性能。

1D MRDDATN可以从低像素特征中提取并对齐多个表示分布,而且可以动态地衡量每个子结构的边缘分布和条件分布的相对重要性。

2.3 目标函数

模型的目标函数分为2个部分,第一部分是对源域数据的分类损失,即交叉熵损失;第二部分为源域和目标域在MRDAM的多表示动态分布距离损失之和。

在数学上,源域的交叉熵损失函数表达式为:

(8)

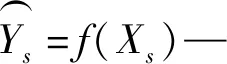
交叉熵损失公式为:

(9)

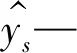
最终,目标函数为:

(10)

式中:μi—第i个子结构中分布权衡因子μ。

λ是大于0的超参数,其公式为:

(11)

式中:steps—迭代的总次数;step—迭代过程中当前的训练周期数。

网络模型训练完成后,由于1D MRDDATN中存在与式(8)相对应的算法代码,模型可以区分源域中不同标签的样本。同时,在目标函数中加入与式(7)相对应的算法代码进行优化,使得目标域和源域的特征分布变得相似。

因此,1D MRDDATN可以准确预测目标域中无标记的样本。

3 实验及结果分析

3.1 实验设置

此处的实验平台为Windows10 64位操作系统、内存为16 GB,显卡为GTX1060 GPU (NVIDIA),编程实现语言为Python,深度学习框架为PyTorch。

由于神经网络输出层激活函数为SoftMax,则损失函数为分类交叉熵(categorical_crossentropy)损失函数。1D MRDDATN选用的优化器为Adam优化器,训练的Batch Size为100,Epoch设置为50,学习率lr设置为动态学习率衰减,初始值为0.01,衰减指数为0.88。

3.2 实验验证

笔者使用的数据集来源于美国凯斯西储大学(CWRU)的轴承数据中心[22]。

滚动轴承故障模拟实验台如图3所示。

图3 滚动轴承故障模拟实验台实物图

实验台由电机、扭矩传感器/编码器、测功机和控制电子设备组成。该实验验证使用了采样频率为48 kHz的驱动端轴承的故障数据。

迁移学习任务设置如表2所示。

表2 CWRU数据集迁移学习任务设置

实验采集了0 HP、1 HP、2 HP和3 HP这4种工况下的故障数据,对应的转速分别为1 797 r/min、1 772 r/min、1 750 r/min和1 730 r/min,因此,全部数据可以被分为4个数据集,即A,B,C,D。

在CWRU数据集中有3种故障状态,分别为内圈(IR)故障、滚动体(Ball)故障、外圈(OR)故障。上述故障均通过电火花机(EDM)加工而成,每一种故障类型根据损伤直径分为3种不同程度故障类型,损伤直径分别为0.177 8 mm,0.355 6 mm和0.533 4 mm(0.025 4 mm=1 mil)。

数据集类别的标签设置如表3所示。

表3 CWRU数据集类别的标签设置

在每个数据集中,数据都包括健康(Health)数据和3种故障数据,而每种故障数据包含3类,则标签共有10类。

在48 kHz采样频率下,每类轴承状态的信号长度大约为480 000。滚动轴承的最低转速为1 730 r/min,在一个转动周期下采集到的时间序列长度大约为1 665。以1 665作为最短样本长度,则一类信号序列可以分割为288个样本。由于每个数据集共有10类轴承状态,则每个数据集共有2 880个样本。

在每次实验中,笔者分别从4个数据集中选择2个不同的数据集作为源域和目标域,则一共有12组迁移任务。在跨域任务中,A→B表示数据集A为源域,数据集B为目标域。

笔者将该模型与深度迁移学习方法(deep domain confusion[23],DDC)、深度适应网络(deep adaptation network[24],DAN)、深度相关对齐领域自适应(correl-ation alignment for deep domain adaptation[25],D-CORAL)、动态分布领域自适应网络(dynamic distribu-tion adapt-ation network,DDAN[19]6)、多表示的领域自适应网络(multi-representation adaptation network,MRAN[21]6)进行对比,并采用了整体分类准确率来评估这些方法的性能,对每次诊断任务运行5次,并求得当次任务准确率的平均值,最终获得每种方法在12组迁移任务中的平均准确率。

6种深度迁移学习方法在多组迁移任务的预测准确率,如表4所示。

表4 模型在多组迁移任务的预测准确率(%)

由表4可以看出:深度迁移学习方法都取得了80%以上的准确率,这说明深度迁移模型可以很好地从源域数据中学习故障信息,帮助模型在目标域获得较高的故障诊断精度;传统的只考虑边缘分布的方法中,DDC、DAN、D-CORAL的准确率都为80%～90%,而考虑边缘和条件分布的DDA和只考虑条件分布的MRA的平均准确率比只考虑边缘分布的方法准确率高,证明了条件分布对整体数据分布有重要的影响;1D MRDDATN对于每组迁移任务的预测准确率均在96%以上,平均准确率在98%以上;而DDA和MRA的平均准确率都比1D MRDDATN低,证明了MRDA方法的有效性。

6种迁移学习网络模型完成一次总训练周期的运行时间,如表5所示。

表5 迁移学习方法运行时间

深度学习问题追求的目标都可以分为两个阶段:(1)性能;(2)效率。

在模型性能最强、准确率最高的前提下,1D MRDDATN虽然计算效率稍微下降,但与其他的迁移学习方法相比,其整体性能最强。

为了直观地验证所提方法的有效性,笔者以任务B→C为例,利用混淆矩阵分析这6种方法在具体类别上的表现差异。

6种迁移学习方法混淆矩阵如图4所示。

图4 6种迁移学习方法混淆矩阵对比

从图4的混淆矩阵可以看出:笔者所提出的1D MRDDATN对绝大多数类别的预测准确率都比其他方法高,每个类别的预测准确率都不低于96%,而其他的方法至少在一类上的预测准确率低于90%。

总体来看,1D MRDDATN对每种故障类型的预测都能取得不错的效果。

同样,以任务B→C为例,笔者使用t-SNE[26]技术将全连接层的特征映射到二维空间。

6种迁移学习方法特征可视化的结果如图5所示。

图5 6种迁移学习方法特征可视化对比圆圈——源域特征;三角形——目标域特征;不同颜色代表不同的类别

从图5中可以看出:DDC、DAN和D-CORAL方法在源域学习的分类模型在目标域上未能取得很好的效果;DDAN和MRAN方法对每种类型的数据特征在空间上具有很好的聚簇性,但是部分数据特征存在重叠现象[27，28];

1D MRDDATN使源域和目标域的分布更接近,减小源域和目标域的分布差异,增加不同类别之间的距离,获得更好的聚类结果,这进一步证明了该方法的有效性。

4 结束语

在不同的工况下,要收集足够多标记的滚动轴承故障样本是非常困难的,为此,笔者基于域自适应的方法提出了1D MRDDATN。

该方法在CWRU数据集中与主流迁移学习方法进行了对比,结果表明,该方法平均预测精度最高,证明了所提出的方法在不同工况下滚动轴承故障诊断的有效性。

研究结果表明:

(1)基于DDA方法,利用多表示结构和一维空洞卷积,构成了轻量级1D MRDDATN。通过对比实验,验证了该方法具备更高的准确率;

(2)采用滚动轴承的原始振动信号作为1D MRDDATN的输入,避免了一维振动数据的预处理转换,满足了端到端学习的需求;

(3)MRDAM利用多个子结构动态对齐源域和目标域的多个表示分布,MRDA可以自适应评估每个子结构上边缘分布和条件分布的相对重要性,有效地实现了滚动轴承故障诊断的目的。

上述研究中,笔者研究的是同一设备不同工况下进行迁移学习故障诊断的方法,没有考虑跨设备等复杂工况。因此,在后续的工作中,笔者将针对跨设备、变工况等方面展开故障诊断研究。