基于Halton序列改进蝠鲼算法的K-means图像分割
董跃华,李 俊,朱东林
(江西理工大学信息工程学院,江西 赣州 341000)
0 引言
近年来,图像分割备受研究者关注,其对未知世界具有重要意义,作为图像处理的关键步骤,其目的是从图像中提取感兴趣的目标信息,如今在医学、农业、海洋等领域有重要研究价值。聚类图像分割也已经得到成功的研究。其中,K-means是最常见且最简单的聚类方法[1],但K-means存在随机性较大且易陷入局部最优的缺陷,无法合理地控制聚类中心。随着研究的不断深入,智能优化算法在数据挖掘、路径优化、图像处理等领域被广泛应用,由于其在优化方面表现卓越,很多学者将其应用到图像处理领域,该类算法已成为科研领域的研究重点。文献[2]采用萤火虫算法对K-means聚类算法进行优化,使得其在医学图像分割问题中具有更好的性能指标;文献[3]提出了一种新型的动态粒子群优化算法,用于优化K-means图像分割的质量,较传统的K-means聚类分割算法具有更好的直观效果,解决了传统K-means聚类在图像分割中分割质量和效率方面的问题; 文献[4]对灰狼优化(Grey Wolf Optimizer,GWO)算法进行改进,用于卫星图像的聚类分割;文献[5]采用正余弦算法(Sine Cosine Algo-rithm,SCA)解决传统聚类方法存在的聚类中心不合理和收敛速度慢等问题;文献[6]为解决K-means聚类效果的缺陷,提出了一种新型改进麻雀搜索算法(Modified Sparrow Search Algorithm,MSSA),采用Logistic的自适应因子及小孔成像反向学习提升了麻雀搜索算法的寻优能力,使得优化后的K-means图像分割的质量更佳。上述研究证实了智能优化算法对传统的K-means 聚类算法进行优化,能取得较好的聚类及图像分割结果。
蝠鲼觅食优化(Manta Ray Foraging Optimization,MRFO)算法是最近流行的一种群智能优化算法,具有灵活的搜索能力,全局搜索能力强,但是缺乏局部开发能力[7]。例如个体之间顺序搜索,依赖性较大,缺乏主动性,导致整体搜索范围较好,但局部搜索性能较差。当前,研究者们已经注意到这一点,陆续开展研究,例如文献[8]将分数微积分(fractional calculus)与MRFO进行结合,来修正蝠鲼运动的方向,通过CEC 2017测试函数验证了该算法的可行性,将其应用于图像分割问题中具有良好的效果;文献[9]提出一种基于图的并行分割算法,该算法采用并行结构,将图像分为多个区域,充分利用不相邻区域的处理具有并行性的特点,对多个区域进行并行处理;文献[10]将梯度优化器与MRFO结合,以此来降低算法陷入局部最优的概率,在单目标及多目标的经济排放调度中,具有较好的效果;文献[11]采用自适应加权及混沌思想改进MRFO,从而高效地处理热力学中的问题;文献[12]采用反向学习初始化种群,增大种群的多样性,将其应用于阈值图像分割问题中,具有较好的分割质量;文献[13]在MRFO中加入了一种攻击能力,使其跳出局部最优找到全局最优解,进而应用于3D Tsallis的图像分割问题中;文献[14]将SA融合MRFO,并应用于PID控制器中,融合之后的算法明显优于其他算法的控制;此外,文献[15]采用反向学习及融合模拟退火算法,提高了算法的收敛速度,将其应用于分数阶比例积分导数(FOPID)控制器中,具有较好的控制性能。虽然这些工作能够取得一定的成效,但不能完全平衡算法的局部搜索和全局搜索,当面对高维复杂问题时,解的质量存在不可靠性。
1 标准蝠鲼觅食优化算法
MRFO算法模拟蝠鲼在海洋中不同的捕食策略,通过不同的合作方式进行觅食,从而实现对一定空间内解的搜索。该算法主要分为链式觅食、 螺旋觅食和空翻觅食3个阶段。
1.1 链式觅食(Chain foraging)
蝠鲼群体觅食时,第一个蝠鲼向最好的食物源挪动,而其他蝠鲼则向最好的食物源和它前方的蝠鲼移动,依次形成一条链状的捕食链。具体数学模型可表示为

(1)
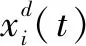
1.2 螺旋觅食(Cyclone foraging)
在一定空间内,蝠鲼群体中的每一个蝠鲼发现优质食物源时,会首尾相接,呈螺旋形状向食物源汇聚。蝠鲼种群在汇聚的过程中,其运动方式逐渐从单一的链条状转变成螺旋状,围绕最佳的食物源开展搜索。螺旋觅食过程的数学模型可表示为

(2)
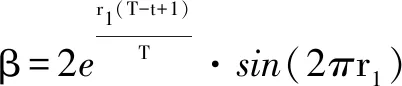
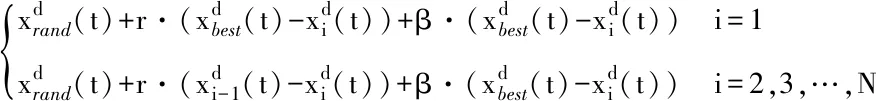
(3)
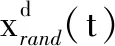
1.3 空翻觅食(Somersault foraging)
当某个蝠鲼发现食物源后,将食物源视作一个支点并绕其旋转、空翻至另一个新位置,以引起其他蝠鲼的注意。对蝠鲼群体而言,空翻觅食是围绕食物源展开多样的搜索,它可以有效改善下一次蝠鲼群体的搜索方式。其数学模型为
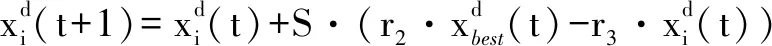
(4)
式中:S为空翻因子,决定空翻的距离;r2和r3是服从[0,1] 均匀分布的两个随机数。随着S取值不同,蝠鲼个体会空翻至搜索空间中与当前位置关于最优解对称的位置。
2 基于Halton序列改进蝠鲼觅食优化算法
2.1 Halton序列初始化种群
原始蝠鲼觅食优化算法采用随机函数初始化种群,该方法得到的种群分布具有较大的随机性,能够覆盖到一定的空间范围,但是它的不确定性也同样存在,不能保证每次随机初始化种群后的分布都是均匀的,甚至密集性较大,从而导致种群搜索速度慢,种群多样性不足。针对上述问题,本文引入Halton序列产生伪随机数来初始化种群,该方法充分考虑了个体分布的均匀性,伪随机数的遍历性能够使个体均匀地分布在空间内的不同位置,这样能够提升初始种群的质量,为后续算法的搜索提供有效的条件,加快了算法的收敛速度[16]。
对于二维的Halton序列,其实现过程为:选取两个质数作为基础量,通过对两个基础量不断展开,从而组合成一系列均匀分布且不重复的点,其展开过程数学模型描述为[17]
(5)
σ(n)=c0x-1+c1x-2+…+cmx-m-1
(6)
H(n)=[σ1(n),σ2(n)]
(7)
式中:n∈N;x为大于等于2的质数,表示Halton序列基础量;ci∈{0,1,2,…,p-1},为常数;σ(n)为定义的序列函数;H(n)为最后得到的二维均匀Halton序列。为清晰地描述Halton初始化种群的优势,给出算法采用Halton的个体分布图。初始种群分布如图1所示。两个基础量分别为2和3。
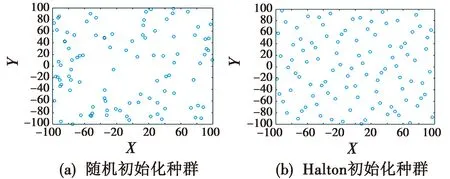
图1 初始种群分布图Fig.1 Initial population distribution map
从图1中可以清晰地看出,Halton生成的种群位置非常均匀,而随机初始化的部分个体位置相对集中,Halton序列能够使算法更好地开发出不同位置的解,提升算法的全局性搜索能力。
2.2 基于折射原理的反向学习
反向学习(Oppposite-Based Learning,OBL)是一种常用的改进智能优化算法的方法,这种计算当前位置的反向解的学习方式能很好地提升算法的搜索范围,使得算法的寻优性能在前期得到提升[18]。虽然优化性能有所提升,但方法单一,缺乏灵活性,在后续优化中存在陷入局部优化的可能。为了解决上述问题,本文采用折射反向学习(Refracted Oppposite-Based Learning, ROBL)[19-20]来更新发现者的位置。原理是把光的折射定律引入到反向学习中,利用折射定律开发更深层次的解。具体原理如图2所示。

图2 折射反向学习原理图Fig.2 Schematic diagram of refracted oppposite-based learning
在图2中,X轴上的解的搜索区间为[a,b],Y轴表示法线,l与l′表示入射光线与折射光线的长度,α和β分别为入射角和折射角,O为[a,b]的中点,由图中的几何关系及折射率的定义可知
(8)
令p=l/l′,代入上式可得
(9)
将公式进行变形,得到折射反向解为
(10)
显然,p=m=1时,可转换为一般的反向学习,由此看出,一般的OBL得到的解比较固定,手段单一。而ROBL则可以通过调整参数动态获取新解,降低算法陷入局部最优的概率。当优化的问题维度上升,折射反向学习算式为
(11)

2.3 新型高斯变异
变异是群智能优化算法常用的手段,主要是用来摆脱算法原有机制的束缚,开拓出新的搜索方式[21]。MRFO算法在前期具有较好的搜索能力,但后期个体寻优接近最优解,个体之间相互靠拢,这样就可能陷入局部最优。因此,本文引入一种新型的高变异函数GMFi(t)[22],能够有效改善此类情况,通过指数函数改变后期个体搜索范围,跳出局部最优状态。GMFi(t)具体算式为
(12)
xi(t+1)=GMFi(t)xi(t)
(13)
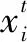
2.4 改进的蝠鲼觅食优化算法
为提升蝠鲼觅食优化算法的寻优能力,本文提出了一种Halton序列蝠鲼觅食优化(HMRFO)算法,该算法采用Halton初始化种群,使得个体分布均匀,为寻优做好充分的准备;再采用折射反向学习增大个体的搜索能力,最后采用新型高斯变异来降低算法陷入最优的概率,综合提升算法的寻优能力。具体伪代码流程如下。
Algorithm:The framework of the HMRFO
Input
M:最大迭代次数
N:种群数量
Output:Xbest,fg
采用Halton序列初始化种群
t=1;
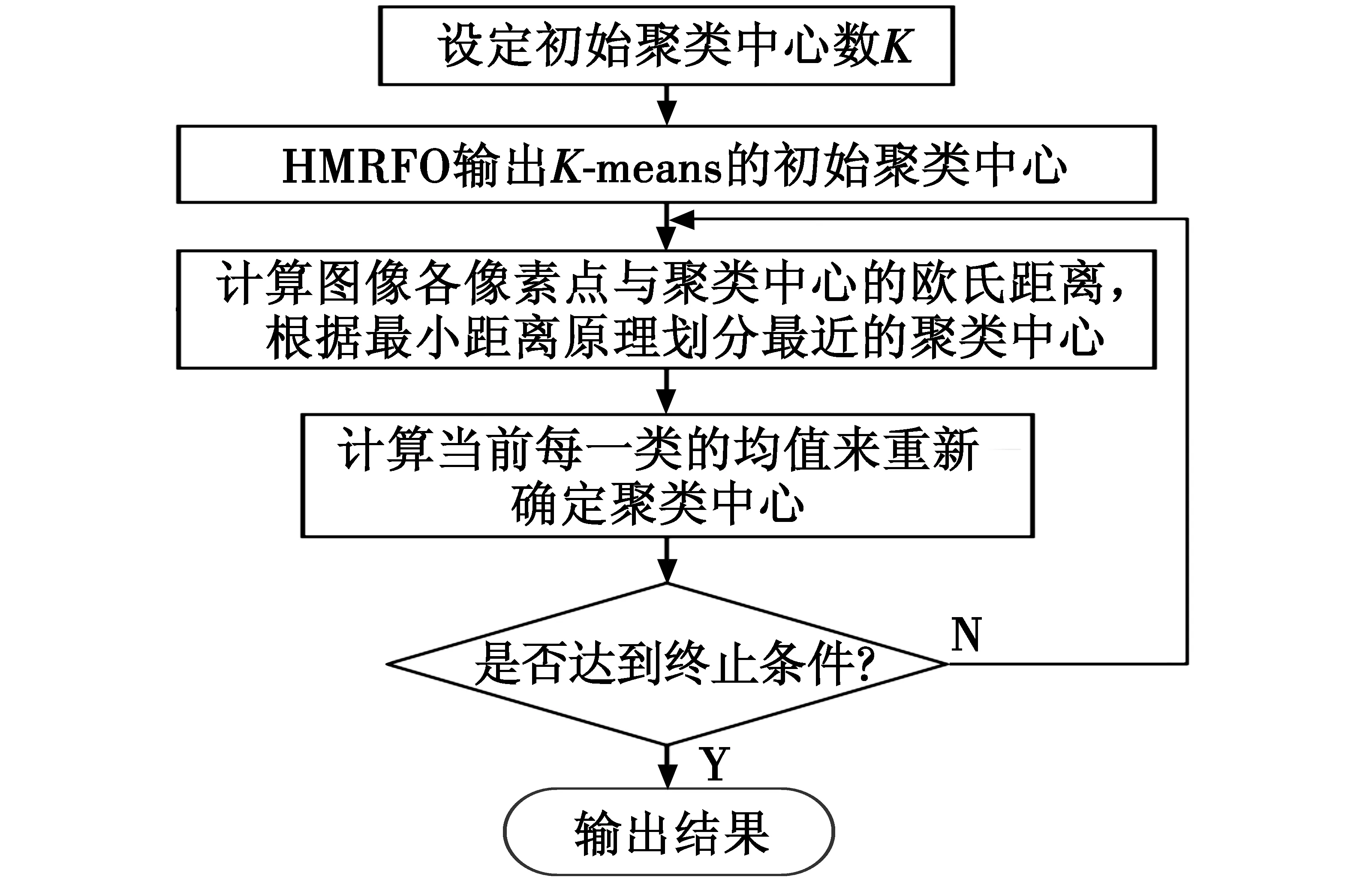
While(t Fori=1 toNdo If rand<0.5 then Ift/M 根据式(3)更新个体位置 Else 根据式(2)更新个体位置 End if Else 根据式(1)更新个体位置 End if 根据式(11)更新个体位置 Compute the fitness of each individual,getXbest,fg,Xworst Fori=1 toNdo 根据式(4)更新个体位置 End for 根据式(13)更新个体位置 Compute the fitness of each individual; Get a newXbest,fg; End while Get the finalXbest,fg。 传统K-means算法的原理是随机选择K个聚类中心,这样选取的方式具有不确定性,导致最后的结果存在较大的差异,且容易陷入局部最优。因此需要选择合适的初始聚类中心。智能优化算法已经成功地应用于K-means中,改善了其随机性与陷入局部最优的缺陷。本文采取改进的蝠鲼觅食优化算法对K-means进行优化,使得初始聚类中心得到良好的控制。其目标函数为 (14) 式中:Xi为图像的一个像素灰度值;Yj为第j个聚类中心。利用HMRFO得到最佳初始聚类中心数使其目标函数的适应度值最小。具体分割流程主要包括以下两部分: 1) 通过HMRFO的全局搜索能力对初始聚类中心进行优化,找到图像点集中合理且最佳的初始聚类中心位置; 2) 将HMRFO输出的初始聚类中心在K-means算法中进行图像分割。 具体流程图如图3所示。 图3 基于HMRFO的K-means图像分割流程图Fig.3 Flow chart of K-means image segmentationbased on HMRFO 时间复杂度是衡量一个算法的重要指标,因此需要平衡算法的寻优能力与时间复杂度,才能说明得到有效的提升。基本的MRFO仅分为链式觅食、螺旋觅食及空翻觅食3个阶段,其中链式觅食与螺旋觅食在同一个循环内。设种群数量为N,最大迭代次数为T,维度为D,因此MRFO的时间复杂度可以归纳为 O(MRFO)=O(T(O(cyclone foraging+chain foraging)+ (15) 设引入折射反向学习的计算时间为t1,引入新型高斯变异的计算时间为t2,原算法与改进后算法的初始化阶段可忽略不计。 因此HMRFO可以归纳为 O(HMRFO)=O(T(O(cyclone foraging+ (16) 可以看出,HMRFO的时间复杂度没有发生根本的变化。对于迭代次数较大的情况,小幅度的增加可以忽略不计。若能有效地提升算法的寻优能力,这些增加会具有重大意义。 为了验证HMRFO算法的有效性及可行性,本文选取了6个基准测试函数来验证其函数优化能力。具体测试函数信息如表1所示。为了证明HMRFO具有竞争性,将其与MRFO,GWO,Particle Swarm Optimization(PSO)[23],Whale Optimization Algorithm (WOA)[24]这4种算法进行对比。各算法的迭代次数与种群数量分别为500,100。实验环境为Window10 64bit,软件为Matlab2019b,内存为16 GiB,处理器为Intel®CoreTMi5-10200H CPU@2.40 GHz。各算法的寻优结果如表2所示,分别计算了各算法30次运行结果的平均值、最优值和标准差。 表1 测试函数信息Table 1 Test function information 表2 各算法寻优结果Table 2 Optimization results of each algorithm 为了能清晰地看出各算法在各函数中的寻优情况及收敛效果,给出了各算法的平均收敛图,如图4所示。 从图4中可看出,HMRFO的收敛效果较好,基本都能最快找到精度最高的解,尤其在F4(x)~F6(x)这些函数中,收敛效果具有较大的优势。可见,灵活的搜索机制使得算法在寻优过程中迅速找到最优解,从而证明了HMRFO的有效性。 图4 各算法收敛效果Fig.4 Convergence effect of each algorithm 目前,图像处理已经应用于多个领域,陆地上的图像已经得到了良好的发展,但在水下图像中仍具有研究价值。因此,为了展现研究价值,本文选取了4幅水下图像作为测试图像,数据来源于文献[25]。选取 PSO,MSSA,MRFO,HMRFO 这4种算法对K-means 进行优化,并实现图像分割,同时也将传统K-means 的图像分割效果一起进行对比。由于聚类中心个数K值对K-means 聚类效果的影响较大,K值选择不当会对结果产生很大的影响,因此本文将K值统一设为3,避免K值的干扰。算法的参数进行统一设置:种群数量为30,最大迭代次数为100。各算法分割效果见图5。 单纯从人的视觉无法判断分割图像的细节差异,因此本文引入了3种常见的图像分割的度量指标PSNR,SSIM及FSIM,用于衡量各算法的分割质量及优化能力。 PSNR主要用于测量分割后的图像与原始图像之间的差值,具体算式为 (17) (18) 式中:ERMSE为像素的均方根误差;M×Q为图像的大小;I(i,j)为原始图像的像素灰度值;Seg(i,j)为分割图像的像素灰度值。PSNR值越大,代表图像分割质量越好。 图5 各算法分割效果Fig.5 Segmentation effect of each algorithm SSIM是处理图像中边缘信息内容的度量。它是通过评估处理图像与原始图像的高频内容(边缘信息)的相似性来测量的。SSIM值越高,说明图像质量与算法优化的性能越好。SSIM的算式为 (19) 式中:μI与μseg分别为原始图像与分割图像的平均值;σI与σseg分别为原始图像与分割图像的标准差;σI,seg为原始图像与分割图像的协方差;c1,c2是用来确保稳定性的常量。 FSIM是反映原始图像和分割图像之间特征相似性的度量指标,用于评价图像的局部结构和提供对比度信息。FSIM的取值范围一般为[0,1],其值越接近于1,代表分割效果越好。FSIM的定义如下 (20) SL(C)=SPC(C)SG(C) (21) (22) (23) (24) (25) 其中:Ω为原始图像的所有像素区域;SL(C)为相似性得分,C为像素点;PCm(C)为相位一致性度量;T1和T2为常量;G为梯度下降;E(C)为在位置C上的响应矢量大小,并且尺度为n;ε为一个极小的数值;An(C)为尺度为n的局部大小。具体分割度量指标如表3所示。 表3 各算法分割性能Table 3 Segmentation performance of each algorithm 在图5中,单纯从肉眼来看,HMRFO优化后的图像更加清晰,尤其是在Test 02~03中,图像整体性较好,其他算法优化后的图像相对过于粗糙。通过表3可直观地看出,HMRFO在4个图像中的最优指标是最多的,尤其在Test 03中,HMRFO优化后的指标均是最好的,K-means的效果最差,其他算法的最佳指标比较少。因此,可以看出HMRFO优化后的K-means图像分割具有较好的普适性,且分割质量较好;同时,也说明了多策略的引入进一步提升了算法的寻优能力。 K-means聚类算法的初始聚类中心随机性较大且容易陷入局部最优,导致图像分割质量较差,为此,本文提出了一种基于HMRFO的K-means图像分割,HMRFO采用Halton序列初始化种群,使得个体分布更加均匀,进一步提升了种群的多样性,再引入一种折射反向学习,提高算法的全局视野,最后采用高斯变异防止算法出现早熟现象,平衡算法的局部与全局性搜索。通过6个标准测试函数验证了HMRFO的有效性及可行性。由其优化K-means的图像分割中可以看出,HMRFO优化后的图像分割质量比其他算法更佳,且普适性较好。但从表3中可看出,同一幅图像中,不一定能保证3个性能指标均是最佳的,因此下一步的工作重点是平衡所提算法在同一幅图像中的所有性能指标。2.5 基于HMRFO的K-means图像分割
3 性能测试与分析
3.1 时间复杂度分析
O(somersault foraging)))=
O(T(ND+ND))=O(TND)。
chain foraging)+O(t1))+O(somersault foraging)+
O(t2))=O(TND)。3.2 基准函数测试

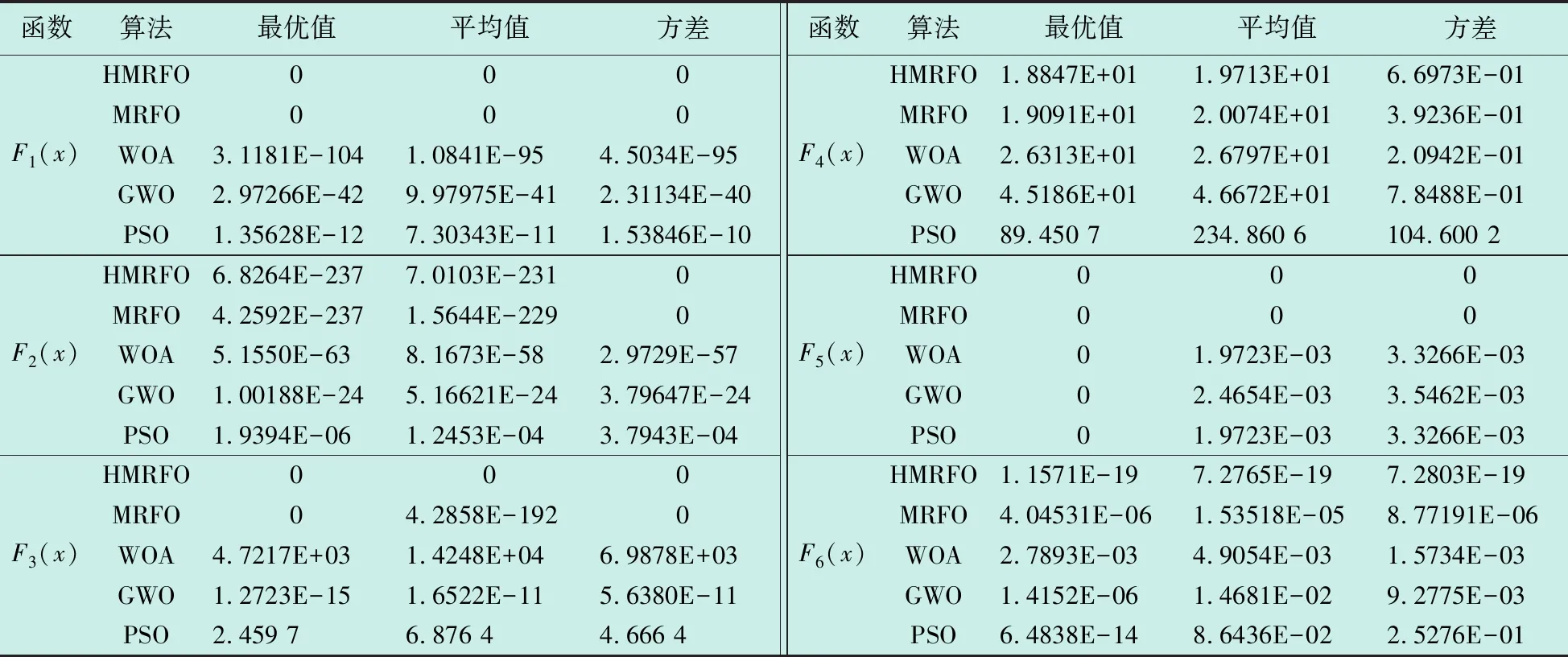
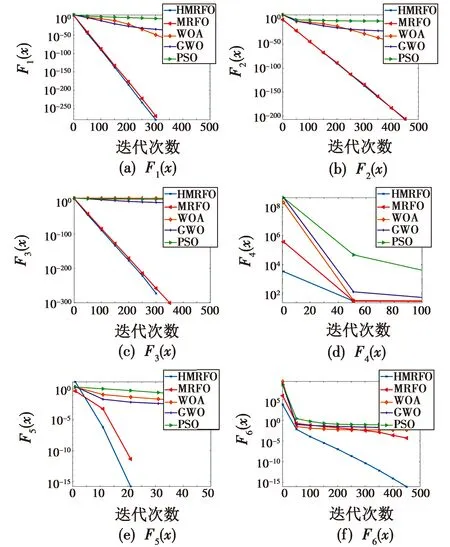
4 图像分割实验


5 结论

