基于三点偏置刀位偏差补偿的五轴侧铣加工路径优化方法＊

陈力智 周立峰 王 东 马 驰 于建华

（中国航发商用航空发动机有限责任公司，上海 200241）

五轴侧铣加工通过刀具侧刃移除工件表面材料，加工效率高、铣削质量好，因而被广泛用于涡轮和叶轮等非可展直纹面零件的加工[1]。由于非可展直纹曲面的扭曲特性，直母线刀具与曲面完全贴合十分困难，但合理规划刀位可以减小刀具与曲面之间的偏差，为达此目的，研究人员提出了诸多侧铣加工路径的生成方法。

Liu X W[2]提出了刀具定位的双点偏置法，Redonnet J等[3]发展了三点偏置法，严涛等[4]则考虑了刀具与曲面之间四点接触的情形，并建立了描述模型，但这些方法仅适用于圆柱刀。圆柱刀与圆锥刀是两种常见的直母线刀具，但后者可以在同样尺寸下保持更高的刚度，因而避障性更好，更适用于叶轮等复杂结构零件的加工。圆锥刀的几何性质较圆柱刀更为复杂，导致适用于圆柱刀的定位方法很难直接用于圆锥刀。常见的圆锥刀定位方法是两点偏置法，尽管三点偏置法可以带来更高的定位精度，但现有关于锥刀三点偏置定位的模型[5]形式复杂，求解困难，限制了其在加工中的应用与集成。值得注意的是，多点偏置得到的刀位往往不能最小化刀具与曲面之间的加工偏差[6]，在使用多点偏置法确定刀位序列后，往往需要对刀轴进行进一步优化。

宫虎等[7]分析了圆柱刀与非可展直纹面几何偏差的性质，给出了偏差极值最小条件下刀轴偏置点的确定方法，并采用最小二乘模型逼近这些散点以确定刀具轴迹面。刘红军等[8]在柱形刀三点偏置定位的基础上，采用密切法进一步优化刀轴以提高加工精度。针对锥形刀五轴侧铣加工，孔马斌等[9]通过对圆柱刀施以旋转确定圆锥刀的初始刀位，然后调整刀轴上的三点减小编程误差。阎长罡等[10]使用两点偏置法确定初始刀位序列，在此基础上提出了基于偏差补偿的刀具轴迹面拟合方法。然后，他们通过构造设计曲面的相伴曲面，建立了基于响应面法的圆锥刀侧铣路径优化模型[11]。因为刀轴与加工误差存在高度非线性的关联，部分学者研究了基于智能算法的侧铣刀路优化方法。Kuo C L等[12]提出了虑及插补误差的侧铣刀位优化模型，并使用粒子群（PSO）法、类电场（EM）法等智能算法寻求最优解。韩军[13]等使用模拟退火算法和粒子群算法（SA-PSO）的混合算法提升了单一智能算法在侧铣刀路优化中的求解效果。

由以上方法可以看出，基于偏差补偿策略的刀路优化方法仍是提高五轴侧铣加工精度的主流手段，但对于锥形铣刀初始定位，缺乏便捷的三点偏置模型；此外，最小二乘模型被广泛用于刀具轴迹面对理想偏置点的逼近，该模型的求解只关注数学意义上的偏差最小，并不能真实反映求解所得路径引起的误差变化。针对以上问题，首先建立解析的圆锥刀两点偏置模型，通过引入滑移区间，搜索得到其三点偏置刀位。在此基础上，分析刀轴偏置点的理想分布，并据此建立轴迹面拟合模型，通过奇异值分解（SVD）算法求解该模型，对比不同求解路径对应的加工误差，选择最小值得到最优加工路径。

1 直母线刀具的三点偏置方法

圆柱刀与圆锥刀均是直母线刀具，圆柱刀可视作圆锥刀锥角为零的特例，因而适用于圆锥刀的定位方法很容易拓展到圆柱刀，本节以圆锥刀为研究对象，提出了通用的刀具定位模型。

首先，非可展直纹面R(u,v)的表达形式如下：

式中：u为沿边界线方向的参数，B1(u)是下边界线，B2(u)是上边界线；v是沿曲面直母线方向的参数。锥形刀的底圆半径为r0，锥角为α，三点偏置条件下刀具与曲面的接触位置分别位于上、下边界线，以及曲面中间的u-曲线R(u,0.5)。假设刀具与曲面在下边界线的接触位置为R(u0,0)，根据锥刀的几何性质，可以计算R(u0,0)对应刀轴上的一点为

式中：Q1为 下边界线对应刀轴上的偏置点，n(u0,0)是R(u0,0)处曲面的单位法矢，曲面上任意一点的单位法矢可由下式计算：

其中：Ru和Rv分别是R(u,v)沿u向与v向的一阶切矢量。如果刀具与曲面的第二接触位置位于曲面上边界线的一点R(u1,1)，则R(u1,1)对 应刀轴上的一点应满足如下方程：

其中：r是R(u1,1)与Q2的距离，其与底圆半径的关系为

将r视作变量x，联立方程（2）、（4）、（5）可得：

其中：

式（6）是一元二次方程，一般存在两解，选大于r0的 正解作为最终解，代入方程（4）得到Q2，进而可以确定当前刀具的刀轴I为I=(Q1Q2)/∥Q1Q2∥，刀具底面圆的中心点O为O=Q1−Irtan(α)。

对于确定的两点偏置刀位，在Q1和Q2限定的区间内对刀轴进行均匀采样，采样点集为计算Pi向设计曲面的投影，如图1所示，所得投影点为Ri，PiRi与刀具靠近曲面一侧的交点为Mi，由此可得与Pi对应的曲面偏差为

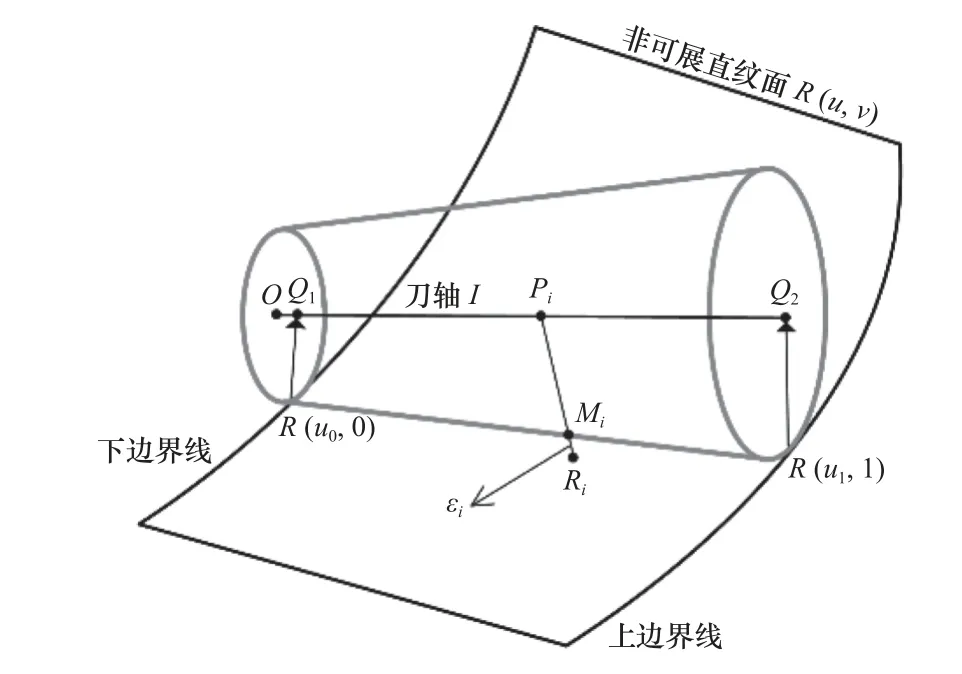
图1 刀具与曲面偏差计算示意图

如果 εi为正，则该偏差表示为欠切；如果εi为负，则该偏差表示为过切；否则，表明刀具与曲面在Ri接触。因此，找到R(u,0.5)在刀轴上的法向偏置点并计算其对应的偏差 εmid，可以判定二者的接触状态。

如果当前刀位下的 εmid不为零，则保持刀具与曲面下边界线的接触位置不变，通过更改上边界线的参数值重新指定刀具与上边界线的接触位置，并计算新刀位下的 εmid，直至搜索到 εmid=0的刀位。其中，改变上边界线参数值的过程类似于刀具沿着上边界线滑动。事实上，当锥角为零，即刀具变为圆柱刀时，所述三点偏置刀位的搜索过程与文献[7]中介绍的三点偏置方法类似，因此，可以应用二分法加速三点刀位的搜索过程。如果在指定滑移范围内，没有搜索到 εmid=0 的刀位，则返回 εmid最接近0时的偏置刀位。图2总结了锥形刀初始刀位的搜索流程，需要注意的是，上边界线的搜索范围[ui,s,ui,e]应保证刀具在ui,s和ui,e对应两 点偏置刀位的 εmid异号。

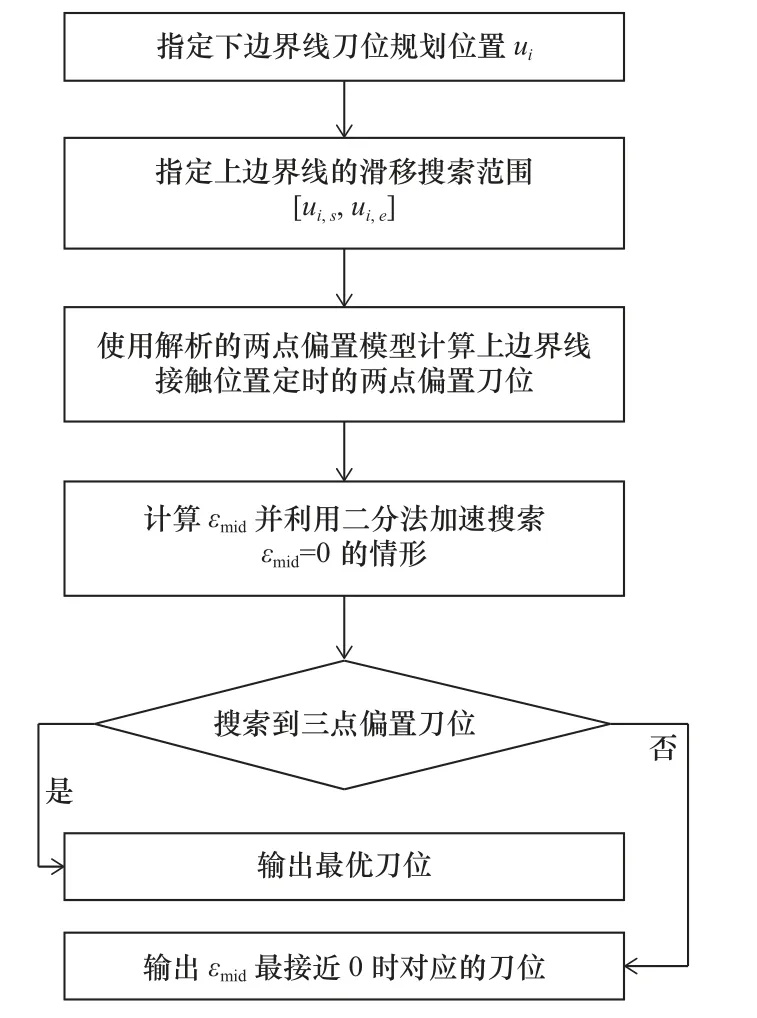
图2 初始刀位规划流程图

2 基于偏差补偿的刀路优化

2.1 加工偏差的近似计算

根据规划所得刀位序列，可构建刀具路径的描述方程。假设刀位个数为m，从规划刀位中获取两组点列，一组是刀具底面圆心另一组是曲面上边界线在刀轴上的法向偏置点使用三次B样条曲线对点列进行拟合，其中，样条曲线控制点的个数不超过规划刀位个数的一半，节点矢量可选用均匀节点矢量。由拟合而来的曲线分别记为Cb(t)和Ct(t)，其表达式如下

式 中：Nl,3(t)和Ns,3(t)是 3次B样条基函数，D1,i和D2,i是控制点，其个数分别为m1和m2。进一步，得到刀路的连续表达式，即

轴迹面方程：

式中：参数a、t分别表示沿刀轴方向和进给方向的参数，可见刀具轴迹面也是直纹面，每一个确定的t值都对应一个刀位。

虽然加工偏差被定义为刀具运动包络面与设计曲面之间的距离，但这种方式下定义的加工偏差计算较为复杂，而刀具与曲面之间的几何偏差亦可精准反映二者之间的贴合程度，因此采用刀具静态轮廓到曲面的距离近似表示真实的加工偏差。与第一节所述的单刀位偏差计算类似，首先对轴迹面沿其t向和a向分别均匀离散，离散个数为n1和n2，其中第i行第j列对应的离散点为D(ti,aj)；然后通过D(ti,aj)作垂直于设计曲面的法线，得到法线与刀具曲(面和) 设计曲面的交点，两交点之间的距离表示Dti,aj对应的法向偏差 εi,j。

2.2 偏差补偿模型

如图3所示，为减小D(ti,aj)对应的法向偏差εi,j，可以将D(ti,aj)沿 -εi,jni,j的方向作移动，其中ni,j表示设计曲面上指向外侧的单位法矢量。考虑到三点偏置定位下，刀具与曲面的偏差值属于微小量，因此，只需对刀具施以微小移动便可以补偿原始偏差。轴迹面上一点的微小移动可用下式描述：

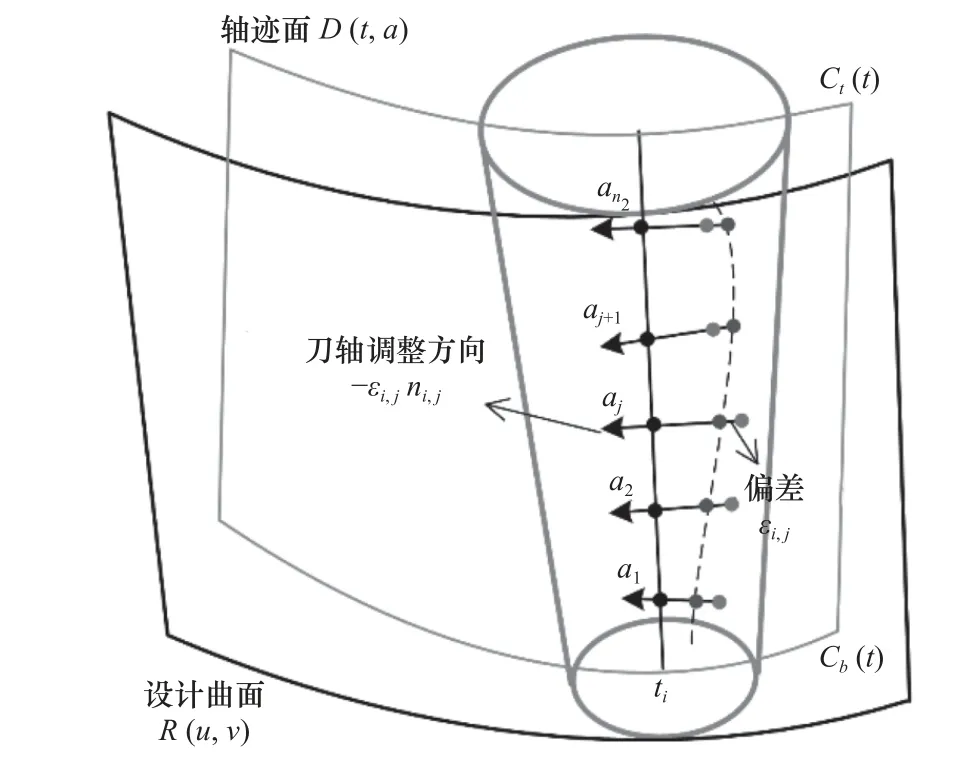
图3 加工偏差的补偿示意图

其中：∆D1,i与∆D2,i是控制点变化量，为未知量。D(ti,aj)微 小移动引起的偏差变化为 ∆D(ti,aj)·ni,j，位置更新后的D(ti,aj)对应的几何偏差值为

对轴迹面上的每一个采样点，均可构造形如式（11）的方程，而最优的刀具路径应保证所有采样点在位置更新后得到的偏差值平方和最小，所对应的优化模型为

其中：n1、n2分别是刀轴面两个方向采用点的总个数。

2.3 SVD求解

针对式（12）所述模型，其极值条件对应的超定线性方程组为

该方程组包含 3(m1+m2)个 方程，式中：A是系数矩阵，b是常值列向量，x是未知变量组成的向量。式（13）的构造方法在其他文献中已有诸多讨论，这里不再赘述。

式（13）的最小二乘解为 (ATA)−1(ATb)，当前该解被广泛视作最优解，但该解仅能从数学意义上表征线性系统Ax对常数向量b的最佳逼近，并不能证明其对应的精度提升效果最好。这里采用SVD对矩阵A进行分解，并据此得到不同的控制点调整量，通过对比这些结果对应的加工误差，筛选出加工精度最优的刀具路径。

为方便叙述，假定A是n3×m3型矩阵，A的奇异值分解结果为其中 ℶ的维度是n3×m3，其主对角线上的非零元素代表奇异值，并由大到小顺次排列。U和V分别是酉矩阵。ℶ中奇异值对应ATA中特征值的平方根。在多数情况下，奇异值随着所处维度的增加而快速衰减，因此可以用最大的k个奇异值和其对应的U、V矩阵部分来近似矩阵A，即通过改变k值，可以得到矩阵A不同的近似矩阵，在此基础上，计算这些矩阵最小二乘解得到的控制点偏移量并用于路径修正，校验路径对应的加工偏差，进而确定其中的最优解。

3 仿真与分析

仿真测试软件为Matlab 2020b，编程计算机的基本配置为：CPU：i5-1240P，RAM：8 GB。测试的非可展直纹面如图4所示。曲面来自于文献[12]中的Surf.5和Surf.6，为避免歧义，本文将这两张曲面记为曲面A和曲面B。曲面A和曲面B的上下边界线均为3次贝塞尔曲线，表1列出了边界线的控制点。因为所提方法的适用对象包括圆柱刀，为更好展示所提方法的优越性，采用半径为2 mm的圆柱刀加工测试曲面，并将加工结果与文献[12]的结果对比。其中，加工精度的表达方式为曲面上所有采样点加工偏差绝对值之和。曲面上采样点的分布与文献[12]保持一致，即对曲面u、v向分别均匀采样，采样个数为。用于路径优化的初始刀位设定为50个，轴迹面上下引导线控制点的个数设为10。表2列出了优化所得路径和文献[12]中方法在加工精度与生成路径所需时间的对比，可见所提方法无论在精度，还是计算速度方面，都显著优于文献[12]所提的基于智能算法的路径优化方法。

表1 测试曲面上下边界线的控制点

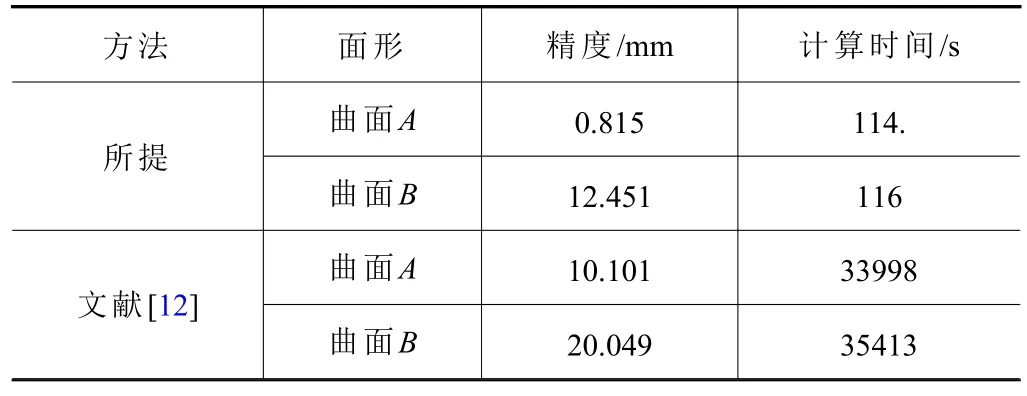
表2 所提方法与文献[12]方法的对比

图4 测试曲面图

图5展示了采用不同k值的SVD分解所对应路径的加工精度，可见最优的加工精度不一定对应原始矩阵A的最小二乘解，而通过对比不同k值下的路径精度，可以筛选得到加工精度提升效果最大的最优路径。

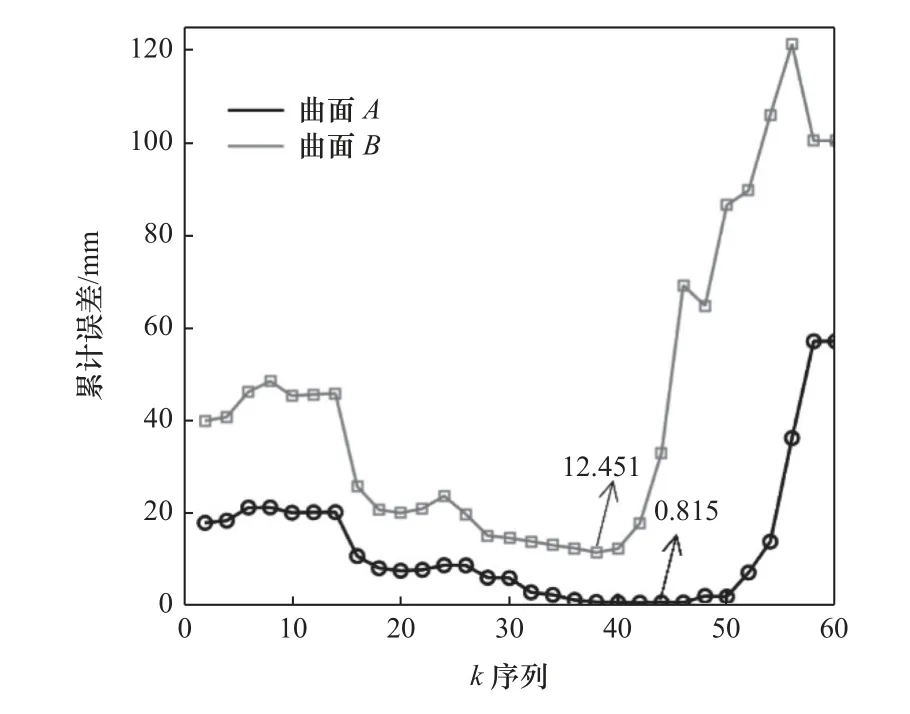
图5 曲面A和曲面B的加工路径在不同k值下的优化效果

同样以曲面A和曲面B为测试对象，当选用刀具为锥形刀时，所提方法依旧有效。在此仿真中，测试参数与圆柱刀的测试保持一致。选用刀具为锥角 α=5，底圆半径r0=1 mm的锥形刀，图6展示了使用三点偏置刀位产生的加工偏差分布，其累积偏差值分别为17.832 mm和30.015 mm；图7展示了在此基础上优化得到最优刀具路径产生的加工偏差分布，优化后的累积偏差为9.651 mm和15.802 mm，可见所提方法能够进一步提升非可展直纹面的加工精度。

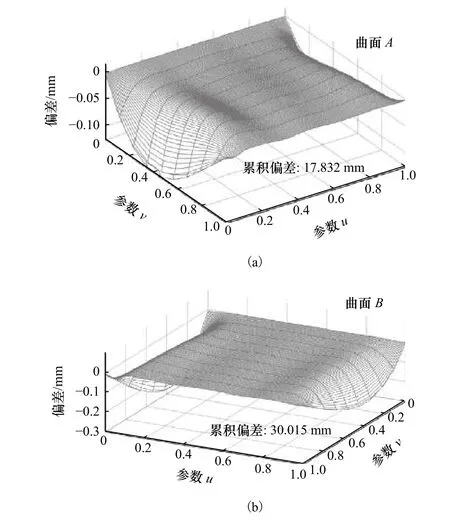
图6 初始刀位下曲面 A和曲面 B的偏差分布

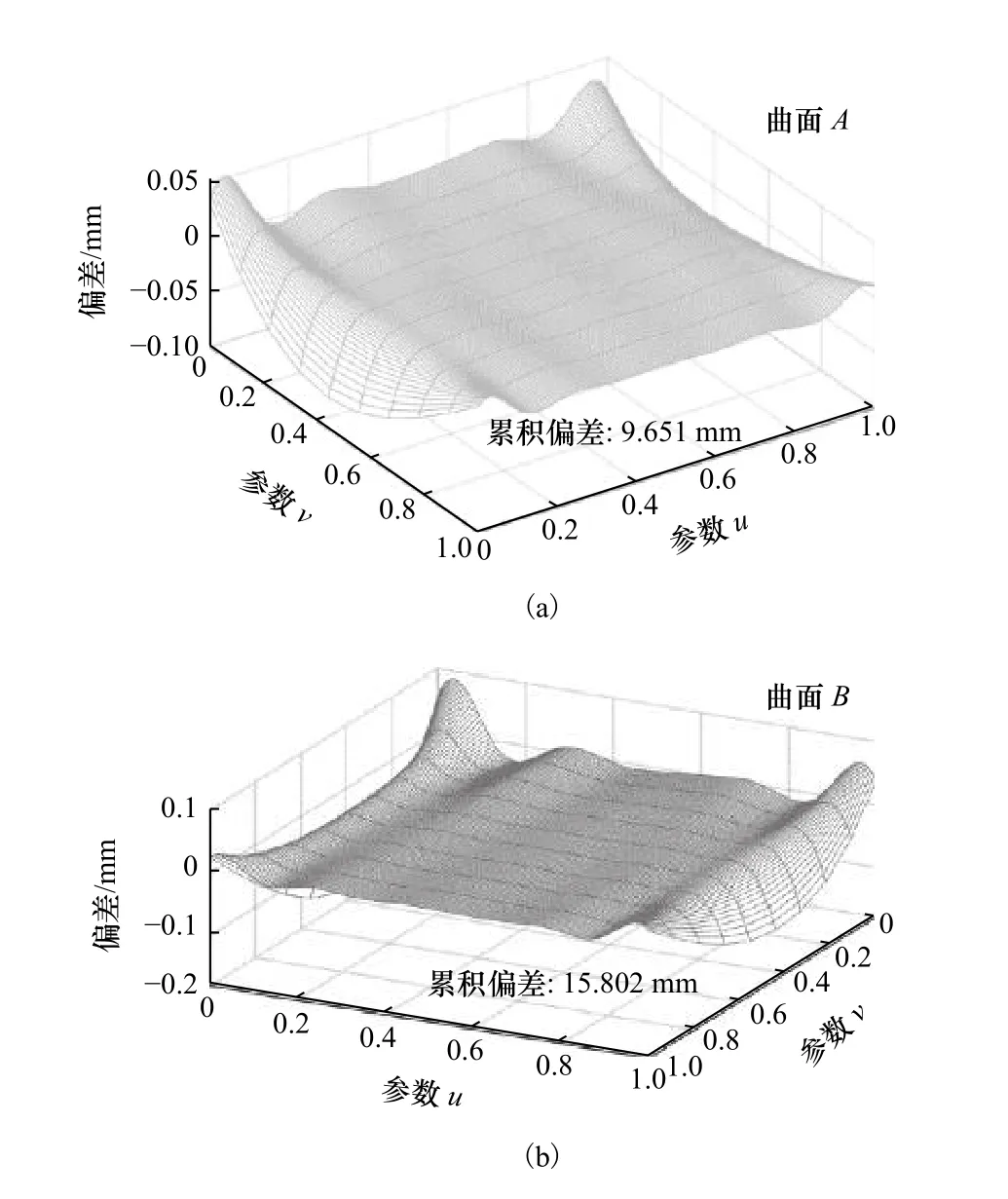
图7 最优路径下曲面 A和曲面 B的偏差分布

4 结语

（1）提出了锥形刀两点偏置定位的解析模型，通过二分法滑移寻优，得到了锥刀三点偏置刀位。所提方法计算效率高，结果准确，生成的三点偏置刀位有助于后续的路径优化。

（2）建立了基于偏差补偿思想的刀轴面优化模型，使用SVD筛选得到了加工偏差最小的刀具路径。在不同测试曲面上与基于智能算法的路径优化方法对比结果表明，所提方法的加工精度提升为38%和92%，并且所需计算时间也大幅减少。