公交拥挤度和通勤者个人特性对时间价值的影响

佘绍芬

（武汉轻工大学土木工程与建筑学院,湖北 武汉 430023）

0 引言

通勤者时间价值是通勤者出行行为分析的基础，对于合理预测通勤者出行选择行为，提高交通系统建设和管理的科学性具有十分重要的意义。以往的研究一般将通勤者的出行时间当作一个常量，随着研究深入，研究者发现通勤者在公共交通中，车厢内拥挤会增加出行者的压力和不满意度，从而影响出行体验和通勤者出行的时间价值[1]。

拥挤度对出行行为的影响，除Haywood等[2]以及Guerra等[3]的文章采用条件评估法外，大部分研究都利用SP（Stated Preference）方法获取数据，用Logit模型研究拥挤度的影响。在出行方式特征上，学者对舒适度对出行行为影响的关注度低，大量研究侧重出行时间的影响。在个体特征对时间价值的影响上，研究者考虑通勤者的收入水平对时间价值的影响，发现收入水平越高，出行的时间价值越高。但通过文献梳理，车厢拥挤会使人的心理状态及驱动性产生压力，进而给出行者带来焦虑、缺少隐私以及自由等心理状态的负面影响，从而影响人的感知[4]。

通过文献梳理该文认为有以下两方面存在不足：一方面，出行者的个人特征可能影响车厢内拥挤度的支付意愿。Kroes等[5]以及Batarce等[6]考虑出行者个体特征的影响，大部分研究成果考虑出行者心理因素的影响较少；另一方面，各国对拥挤度的感知并不一致，蒋盛川等[7]以及邵敏华等[8]等文章研究中国公交系统，其他研究多为发达国家的研究成果。由于生活水平、观念、公交系统服务质量的巨大差异，发达国家的研究成果并不适用于中国。基于以上研究背景，该文利用SP获取数据，研究公交车厢内拥挤度和出行者个人属性对通勤者时间价值的共同影响。

1 问卷设计及数据验证分析

1.1 问卷设计

该文采用SP方法调查数据，选择的影响因子包括车内时间（IVT）、步行至公交站的时间（WT）、车票价格（price）、车厢内拥挤度（density）。考虑到不同类型的公交车的座位数和空间的差异，负荷系数和无座的乘客数量、站立时间等并不能够很好地评价车内拥挤度。因此该文选用站立乘客的密度来表征车厢内拥挤度。

图1为该文的一个SP情景示例，要求出行者在两种公交系统中选择最合意的一种。共设置了16个情景，每个被调查者对4个情景中的选项作出选择。

图1 假定情景示例

根据Shen等[9]的研究，出行者心理因素对出行选择具有一定的影响，在进行Logit模型分析中加入舒适性（comfort）这一潜在变量。潜在变量无法直接观测，为此设置4个表征comfort的测量问题项，如表1所示。采用李克特五级量表进行调查，即1、2、3、4、5分别表示“完全不赞同”“有点不赞同”“不确定”“基本赞同”“完全赞同”。

表1 表征潜变量的测量项

1.2 数据描述性统计分析

调查在武汉市进行，调查时间为上班高峰期，收回问卷1 360份，剔除无效问卷，得到1 200份有效问卷，问卷有效率为88.24%。数据的描述性统计如表2所示。

表2 样本描述性统计分析

1.3 数据的信度和效度检验

为确保数据的可靠性，通过软件对数据进行效度和信度分析，结果如表3所示。问卷测量项信度的Cronbach’sα大于0.7，因子载荷大于0.6，KMO大于0.6，问卷的信度和效度较理想，可进一步分析。

表3 样本数据的信度及效度检验

2 模型分析

2.1 模型基本设定

离散选择模型基于随机效用理论，效用可以分为可观测部分Vin和随机误差项εin两部分。假定出行者n面临一个选择集中的多个出行方式选择i时，会选择集中效用最大的一个选项Uin。则效用函数的表达式为：

考虑出行者的个人属性及车厢内拥挤度等对通勤者时间价值的影响，由公式（1）可知，假定出行者i对于选择集c中第j个选择项的效用的可观测部分可表示为：

根据公式（2），当乘客有座时，Vijc=η·pricejc+λ·Wjc+α·IVTjc；当乘客无座的时候，Vijc=η·pricejc+λ·Wjc+[β0+β1(Zi)·densityjc]·IVTjc。

因此，乘客有座和无座的时候，每小时时间价值（单位：元/小时）可分别表示为：

从公式（3）中可以看出，有座乘客的时间价值为固定值，而无座乘客的时间价值是车内拥挤度的线性函数；当densityjc=0，无座乘客与有座乘客的时间价值不一定相同。

假定β1(Zi)为个人属性的线性函数，即β1(Zi)可表示为：

2.2 潜在变量comfort的确定

由于公式（3）中的comfort为潜在变量，由item1、item2、item3、item4四个显变量求取comfort。通过验证性因子分析得到模型的拟合度参数如表4所示。

表4 验证性因子分析模型拟合参数

2.3 Logit模型及价值分析

根据公式（4）利用Logit模型对数据进行分析，根据表4数据所示，在10%置信水平下，γ2、γ3不显著，即公式（4）中的gender、car对效用函数的影响不显著。删除不显著变量后，对模型进行重新估计，得到结果如表5中模型（2）。

表5 模型估计结果

根据表5数据及公式（3）、公式（4），出行者车内时间价值可表示为：

当通勤者有座时，时间价值为11.9元/小时；当通勤者无座时，时间价值为车内无座乘客密度的线性函数，车厢内无座乘客密度增加1人/平方米，无座乘客时间价值增加值Δ为：

公式（6）中marriage的系数为正，车厢内无座乘客密度增加1人/平方米，相对于未婚者，已婚者时间价值多增加0.96元；freq系数为负，车厢内无座乘客密度增加1人/平方米，相对于经常使用公交的通勤者，不经常使用公交的通勤者时间价值多增加1.12元；comfort的系数为正，车厢内无座乘客密度增加1人/平方米，通勤者时间价值增加0.87comfort，考虑到comfort的变化范围为-1.2～2，comfort的影响不可忽略。

将公式（5）无座情况下的时间价值除以有座情况下的时间价值，得到无座通勤者的相对时间价值（Time Multiplier,TM），如公式（7）所示：

根据公式（7），分析freq、comfort对TM的影响，分别取freq为0、1，comfort取值为0、2，得到相对时间价值TM的对比分析结果如图2所示。

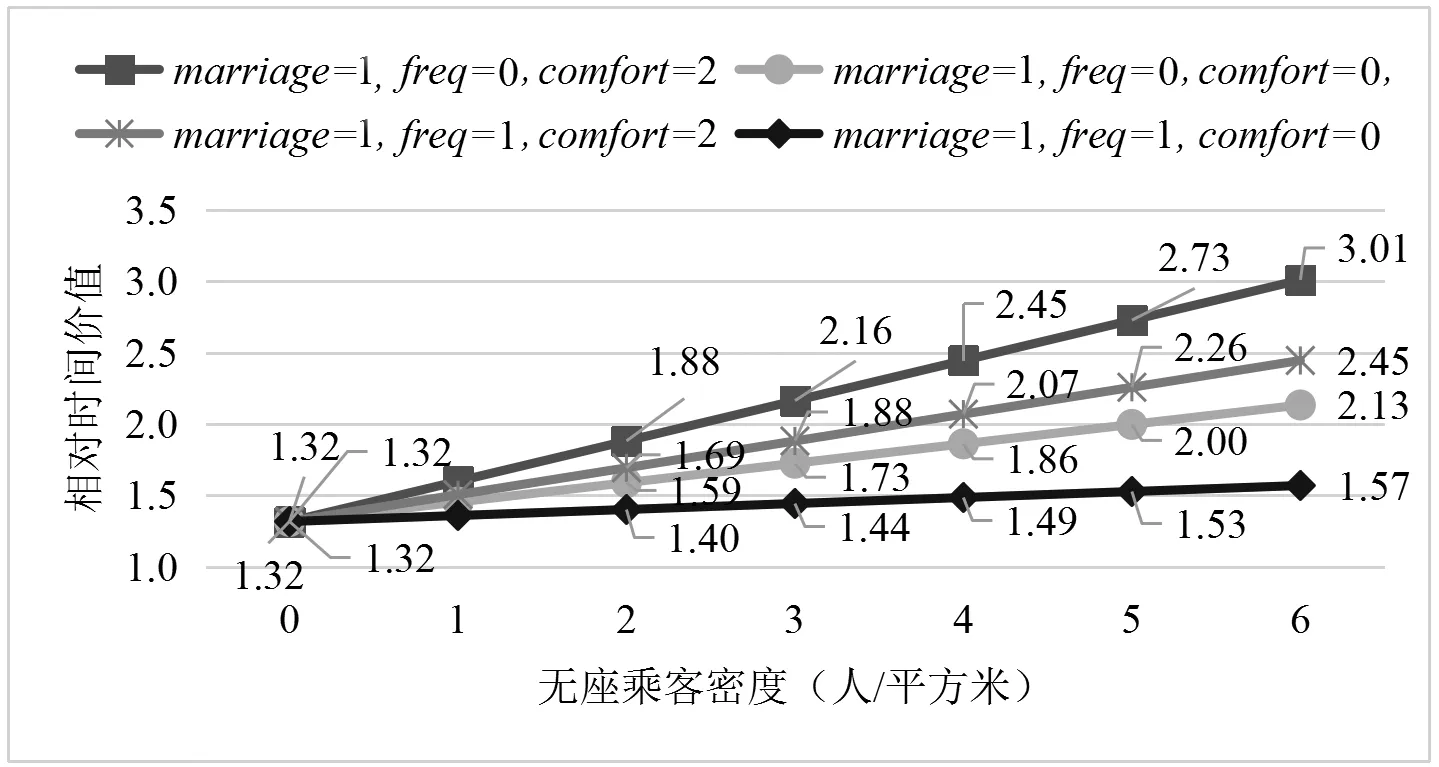
图2 不同密度情况下的相对时间价值

对于已婚、经常使用公交、对出行舒适性要求不高的通勤者，时间价值受拥挤度的影响不大。对于已婚、不经常使用公交、对出行舒适性要求高的通勤者，当无座乘客密度从0人/平方米增至6人/平方米时，相对时间价值从1.32增至3.01。

3 结论

通勤者对于舒适性的主观要求、通勤者的婚姻状况以及是否经常使用公交、公交车厢内的拥挤度等因素对通勤者的时间价值具有显著影响。当通勤者有座时，时间价值为11.9元/小时。当通勤者无座时，时间价值为车内无座乘客密度的线性函数，车厢内无座乘客的密度增加1人/平方米，无座乘客的时间价值增加值为Δ=0.65+0.96marriage-1.12freq+0.87comfort。当车厢内不拥挤时，站立乘客的时间价值是有座乘客时间价值的1.32倍。通勤者对车内舒适度要求越高的，相对时间价值越大。