基于变权理论和集对分析的岩质边坡稳定性评价

李伟华，孙红兵，王建平

(张家口市京新高速公路管理处，河北 张家口 076150)

公路边坡一旦发生失稳破坏，可能导致一些重要的基础设施被损坏以及危及人身安全，造成巨大的财产损失。因为边坡工程的地质较为复杂且与周围环境的相互作用性，使得边坡的稳定性评价成为了岩土工程中比较难攻克的难题[1]。边坡稳定性与地质、环境及工程条件等许多不确定因素的有关，因而，不确定性分析法不断被应用到边坡稳定性的评价中，例如神经网络评价法[2]、模糊综合评价法[3]、灰色系统评价法[4]等。但每种方法大多采用常权重进行边坡稳定性分析，都有一定局限性[5]。

本文以变权理论确定边坡稳定性评价指标权重，结合集对分析方法建立边坡评价的变权理论与集对分析耦合模型，以期对边坡稳定性评价得到更加客观的结果。

1 变权-集对分析耦合模型的建立

1.1 集对分析原理

集对分析方法[6]是我国学者赵克勤提出的一种关于确定-不确定系统同异反定量分析的系统分析方法。集对分析的核心主要是在一个不确定性系统的两个相关的集合之间建立集对，针对建立的集对特性做差异性、同一性、对立性分析，从而建立集对的同异反联系度。

设有联系的集合X和Y。X和Y都有n项表征其特性，即X=(x1，x2，…，xn)，Y=(y1，y2，…，yn)，X和Y构成集对H(X，Y)。定义H(X，Y)间关系的联系度定义为

(1)

式中：μ为集对(X，Y)的联系度；a、b、c为分别称为(X，Y)的同一度、差异度和对立度，a+b+c=1；S、F、P为分别为同一性、差异性和对立性个数，个。S+P+F=N；i差异度系数，i在[-1，1]区间内取值；j为对立度系数，一般取j=-1。

边坡工程是一个具有多种指标的庞杂的系统工程，建立边坡稳定性评价指标(X)与评价集合(Y)的集对(X，Y)。对标准集对分析理论进行改进优化，拓展得五元联系数[7]，表达式如下

μ=a+b1i1+b2i2+b3i3+cj

(2)

式中：a+b1+b2+b3+c=1；b1、b2、b3称为差异度分量，分别表示轻差异度、中差异度和重差异度。

(1)计算单指标联系度

在进行边坡稳定性评价时，要先计算单指标联系度，评价指标标准如表1所示。

表1 评价指标标准

越小越优型指标(反向指标)与评价等级的联系度为

(3)

越大越优型指标(正向指标)与评价等级的联系度为

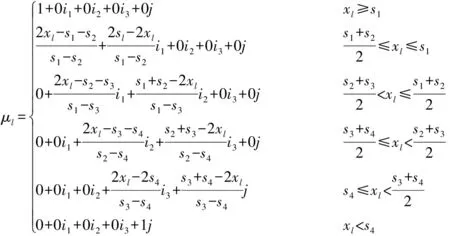
(4)

式中：xl为评价指标l的实测值，其单位随实测指标而定；s1～s5为评价指标l的分级标准，如表1所示。

(2)计算综合联系度

求出各指标的单指标联系度后，构建同异反矩阵向量模型，将各评价指标的权重向量、联系度分量矩阵R及同异反系数矩阵E相乘，即可得出集对H(X，Y)的综合联系度为

μ=W·R·ET

(5)

式中：W评价指标权重总矩阵；E为同异反系数矩阵，即E=(1，i1，i2，i3，…，j)。

根据集对分析理论，由公式(5)得出的综合联系度所对应的评价等级区间即为边坡稳定性等级。

1.2 变权法确定权重系数

指标权重主要通过变权理论确定，引入变权原理中的惩罚与激励机制，通过对惩罚影响较差的指标、激励决策较好的指标来弥补常权决策带来的偏差。

设一组n维变权向量W(X)=[w1(X)，…，Wn(X)]。n维惩罚型状态变权向量是指映射S:[0，1]n→[0，1]n，X→S(X)=[S1(X)，…，Sn(X)]，满足：

(1)xj≥xj→Si(X)≤Sj(X)；

(2)Sj(X对每个变元连续(j=1，…，n)；

(3)对任何常权向量W=(w1，…，wn)，公式(5)满足归一性、连续性和单调性：

(6)

式中：W·S(X)=[w1S1(X)，…，wnSn(X)]称为Hardarmard乘积。同理可定义激励型状态变权向量，即：xj≥xj→Si(X)≥Sj(X)。

状态变权向量是m维实函数的梯度向量，m维实函数是具有连续偏导数的平衡函数。状态变权向量的计算公式如下

(7)

再根据公式(6)即可求出状态变权向量W。

1.3 改进的AHP法

在传统层次分析法的实际应用中，由于判断的片面性，使两者相互比较的结果过于主观和武断，具有主观性和盲目性[8]。故本文采用3标度法，改进常规的层次分析法，通过相应两两方案指标比较，建立比较矩阵，计算最优传递矩阵，进而确定判断矩阵，该方法不需要进行一致性检验，具有良好的判断传递性与标度值得合理性，有利于决策者在两两比较判断过程中提高准确性。

(1)构造3标度的判断矩阵A

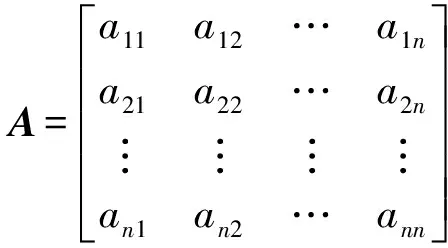
(8)

(2)计算比较可以得到矩阵A的最优传递矩阵R

(9)

(10)

式中：dik=exp(rik)。

(3)根据判断矩阵D，计算系数

计算出该层各元素关于上层次某元素的优先权重，D矩阵中最大特征值所对应的特征向量作为该层各元素的相对权重值，这里采用乘积方根法求解特征向量的值，即

(11)

式中：w=[w1，w2，…，wn]T为特征向量，作为该层次n个元素的权重向量。

2 实例分析

2.1 边坡稳定性评价指标体系

结合京(北京)—新(新疆)高速公路张家口段路基边坡实际，以地质地貌特征、地质环境、气象水文特征3个主要因素综合考虑影响边坡稳定性的11项指标。如表2所示。

表2 边坡稳定性评价指标体系

为了验证基于变权理论和集对分析耦合模型对于边坡稳定性评价的可靠性和合理性，以京新高速公路K23+500～K23+780段的公路边坡为例，进行本方法的实例应用。评价标准如表3所示。

表3 边坡稳定性评价标准及指标实测值

2.2 指标权重的计算

首先采用三标度层次分析法，根据公式(8)～(11)计算常权重，W=(0.192，0.045，0.160，0.134，0.031，0.077，0.065，0.037，0.111，0.093，0.054)。

同时，构造合适的状态变权向量S(Xi)=[S1(Xi)，S2(Xi)，…，Sn(Xi)]如下

(12)

式中：β为否定水平，0<β≤1。在第j项指标状态值xij不高于β时，通过实施变权来增加其权重，从而达到了对其惩罚的目的，本文取β=0.5。α为惩罚水平，无量纲，反映决策对因素均衡性要求的强弱，本文取惩罚水平α=0.7。

结合公式(6)和公式(12)以及常权向量W，可得变权向量

W=(0.183，0.048，0.154，0.161，0.030，0.078，0.062，0.035，0.109，0.089，0.051)。

2.3 边坡稳定性评价

本文根据均分原则法确定差异度系数i，得出i1=0.5，i2=0，i3=-0.5，j=-1。根据实例边坡数据，分别计算各评价指标的单指标联系度，并根据式(5)计算综合联系度。

μ=0+0.093i1+0.29i2+0.471i3+0.145j=-0.334

(13)

将[-1，1]区间进行5等分，(0.6，1)、(0.2，0.6)、(-0.2，0.2)、(-0.6，-0.2)、(-1，0.6)分别对应边坡稳定性评价的I(稳定)、II(较稳定)、III(基本稳定)、IV(不稳定)、V(极不稳定)5个等级。由于综合联系度μ值对应区间为(-0.6，-0.2)，即京新高速公路K23+500～K23+780段边坡稳定性评价属于IV(不稳定)级，稳定性偏向于III(基本稳定)级。与边坡实际情况吻合，说明了该方法的可靠性和合理性。

3 结 论

(1)本文引入集对分析方法，以3标度层分析法为基础结合变权理论确定边坡系统各指标的权重，建立岩质边坡稳定性评价的变权理论和集对分析耦合模型。

(2)以京新高速公路K23+500～K23+780段边坡为例，验证了该模型的正确性和适用性，结果表明运用变权—集对分析模型该边坡稳定性评价属于IV(不稳定)级，稳定性偏向于III(基本稳定)级。该方法计算简便，在对边坡工程稳定性评判方面提供了参考。