灰色系统理论GM(1,1)模型在青海省碘盐监测中的应用初探
王明君
(青海省地方病预防控制所地方病预防控制科,青海 西宁 810000)
碘缺乏病(iodine deficiency disorder,IDD)是由于膳食中或环境缺碘导致碘供应不足,从而导致血液中甲状腺激素水平较低,并对机体造成广泛危害的地球化学性疾病。IDD 一直是我国的重大公共卫生问题,20 世纪90 年代有超过7 亿人缺碘[1],但通过普遍食盐加碘(universal salt iodization,USI)控制碘缺乏病取得了巨大进展。据WHO 报道称,在过去20 年中,世界上已有115 个国家消除了碘缺乏病,缺碘国家的数量已降至25 个[2,3]。概率统计、模糊数学与灰色系统理论是最常用的3 种不确定系统研究方法,其中灰色系统理论通过对“部分”已知信息的生成,通过开发、挖掘蕴含在系统观测数据中的重要信息,实现对现实世界的正确描述和认识。GM 系列模型是灰色预测理论的基础模型,尤其是GM(1,1)模型,应用十分广泛[4]。GM(1,1)模型,即一阶一元灰色预测模型,其中“G”代表Grey,意为灰色,“M”代表Model,意为模型,两个“1”分别表示一阶和一个变量的微分方程模型[5]。从2004 年开始,青海省在全部43 个县(区、市)开展了碘盐监测。以该数据为依据,建立灰色系统理论GM(1,1)模型,并对2012年青海省碘盐监测指标进行预测,初步探讨灰色系统理论GM(1,1)模型在青海省碘盐监测及碘缺乏病防治中的应用效果和价值,旨在为调整防治策略,提高居民健康素养,提高补碘的意识提供理论依据。
1 资料与方法
1.1 资料来源 收集《中国碘盐监测》(1996-2011)青海省2004-2011 年碘盐监测工作总结,选取2005、2007、2008、2009 和2011 年非碘盐率、碘盐覆盖率、碘盐合格率、合格碘盐食用率数据,应用灰色理论与方法建立灰色预测GM(1,1)模型进行拟合检验并预测2012 年各指标变化情况,见表1。

表1 青海省碘盐监测结果(2005-2011 年)
1.2 方法 建立灰色系统理论GM(1,1)模型。其主要步骤包括:①确定原始序列;②累加生成1-AGO 序列;③应用GSTA V7.0 软件得到灰色模型发展系数a、灰色作用量b 和平均相对误差;④计算后验差比值C 和小误差概率P[6]。
1.3 统计学方法 数据整理和录入在EXCEL 中进行,灰色系统理论GM(1,1)模型相关数据计算在GSTA V7.0 软件中进行。
1.4 模拟结果的检验 根据灰色系统理论,模型精度等级分为4 级。一般规定C值越小,P值越大,则模型精度越好[3,6],见表2。
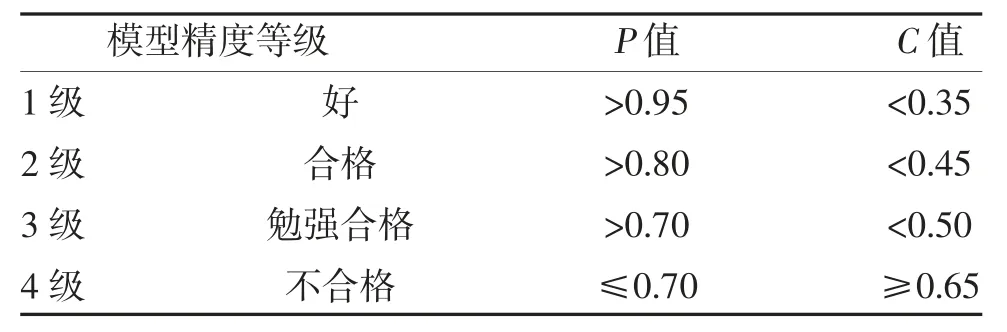
表2 模型精度检验
1.4.1 后验差比值(C)即预测值与实际值之差的集中程度,C 值越小,预测值与实际值之差集中程度越好。
1.4.2 小误差概率(P)即满足残差与残差均值之差小于0.647Sx的个数占总数的比。P值越大,差值越接近0.647Sx,表示模型拟合精度越高。
2 结果
2.1 非碘盐率 初始化建模原始序列为11.84,7.29,3.55,4.44,2.59;原始序列的1-AGO 生成序列为:11.84,19.13,22.68,27.12,29.71;1-AGO 生成序列的紧邻均值序列为:15.49,20.91,24.90,28.42;灰色模型发展系数a=0.32 和灰色作用量b=11.62,平均相对误差为16.47%,见表3。2012 年预测值:1.87%。数据图形模拟见图1。
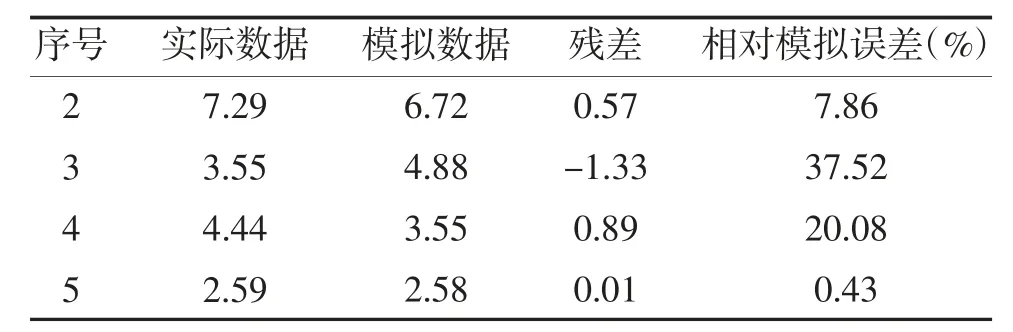
表3 非碘盐率模拟值与模拟误差
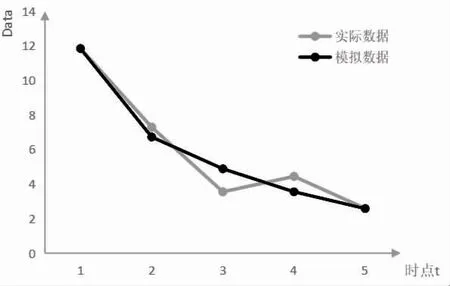
图1 非碘盐率数据图形模拟
2.2 碘盐覆盖率 初始化建模原始序列为:88.16,92.71,96.45,95.56,97.41;原始序列的1-AGO 生成序列为:88.16,180.87,277.32,372.88,470.29;1-AGO生成序列的紧邻均值序列为:134.52,229.10,325.10,421.59;灰色模型发展系数(a)和灰色作用量(b)分别为a=-0.01,b=91.71;平均模拟相对误差为0.83%,见表4;2012 年预测值:98.87%,数据图形模拟见图2。
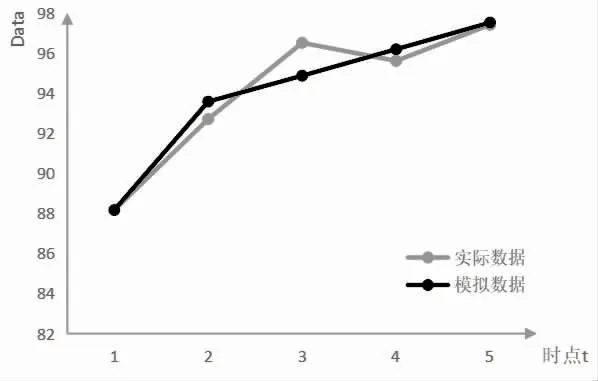
图2 碘盐覆盖率数据图形模拟
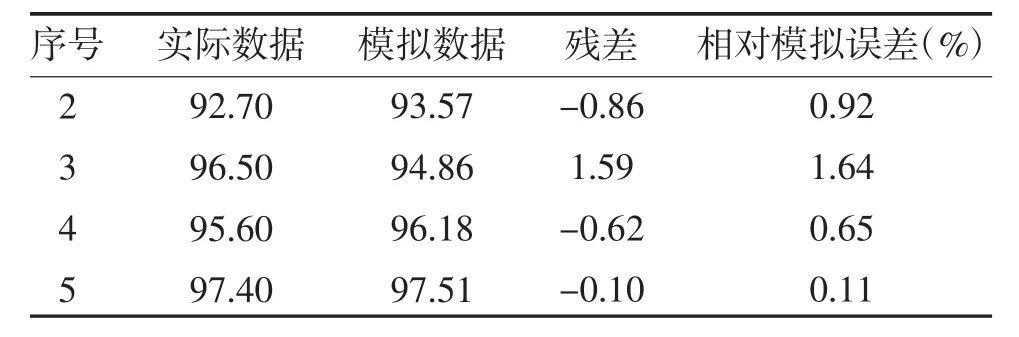
表4 碘盐覆盖率模拟值与模拟误差
2.3 碘盐合格率 初始化建模原始序列为:93.80,94.60,96.58,96.24,96.17;原始序列的1-AGO 序列为:93.80,188.40,284.98,381.22,477.39;1-AGO 生成序列的紧邻均值序列为:141.10,236.69,333.10,429.31;灰色模型发展系数(a)和灰色作用量(b)分别为:a=-0.01,b=94.60;平均模拟相对误差为0.54%,见表5。2012 年预测值:96.99%,数据图形模拟见图3。
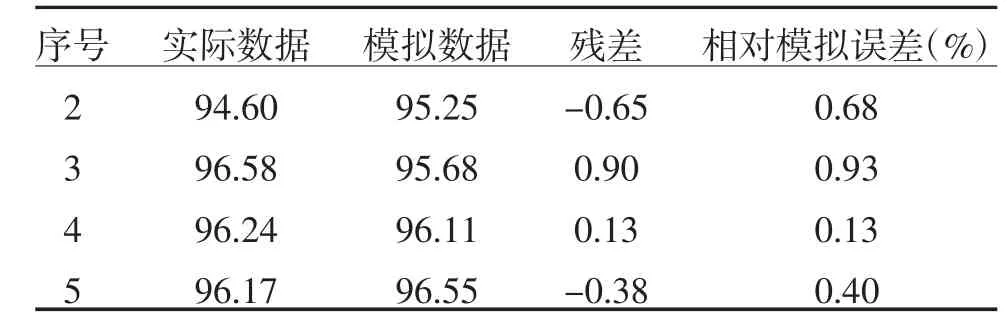
表5 碘盐合格率模拟值与模拟误差
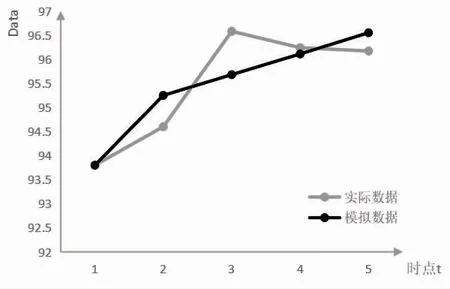
图3 碘盐合格率数据图形模拟
2.4 合格碘盐食用率 初始化建模原始序列为:83.82,87.80,93.19,92.09,93.88;原始序列的1-AGO序 列 为:83.82,171.62,264.81,356.90,450.78;1-AGO生成序列的紧邻均值序列为127.72,218.22,310.86,403.84;灰色模型发展系数(a)和灰色作用量(b)分别为:a=-0.02,b=86.83;平均模拟相对误差:1.27%,见表6。2012 年预测值:96.07%,数据图形模拟见图4
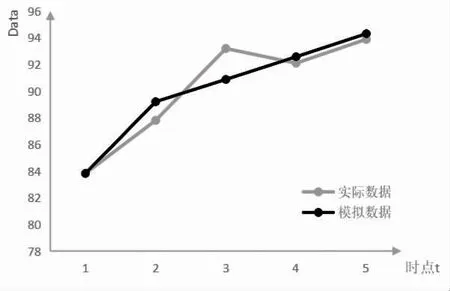
图4 合格碘盐食用率数据图形模拟
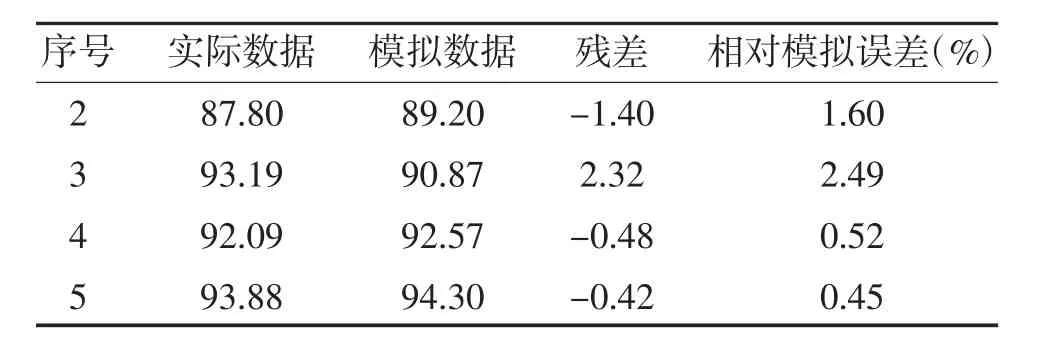
表6 合格碘盐食用率模拟值与模拟误差
2.5 各指标模拟效果评价 非碘盐率P值为0.835,C值为0.111,拟合效果为2 级合格;碘盐覆盖率P值为0.992,C值为0.009,拟合标准为1 级好;碘盐合格率P值为0.995,C值为0.006,拟合效果为1 级好;合格碘盐食用率P值为0.987,C值为0.014,拟合效果为1 级好,见表7。表明所建立的模型精度相对较好,均具有科学、准确的预测效果。
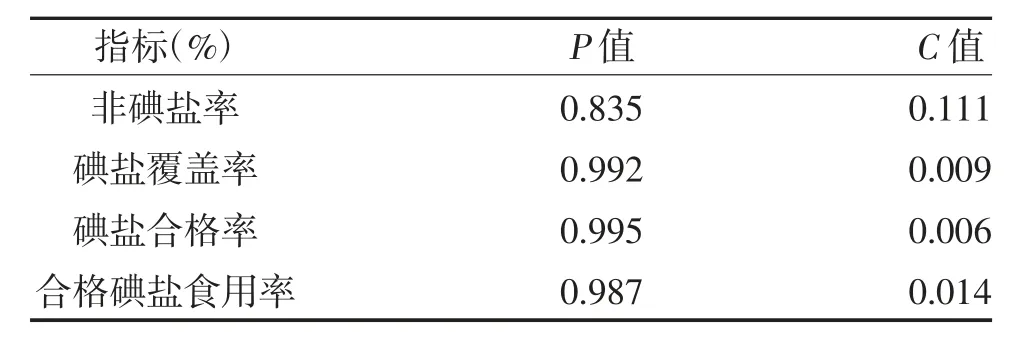
表7 灰色预测GM(1,1)模型拟合结果
3 讨论
在公共卫生领域,对疾病的监测和预警,发病和死亡预测的数学模型较多,主要有灰色系统理论GM(1,1)模型、ARIMA 时间序列模型、BP 神经网络模型等[7]。自灰色系统理论提出以来,GM(1,1)模型成为灰色预测模型的核心和基础理论[8,9]。
碘缺乏病是影响群众身体健康和人口素质的重点地方病,青海省是碘缺乏病流行较为严重的省份之一,在全省范围内均有流行。且因省内盐湖众多,有丰富的盐业资源,非碘盐易得。同时青海省作为少数民族聚居的省份,各族群众生活习惯差异较大,导致加碘盐普及困难,人群碘营养水平一直难以提高,这些都是青海省消除碘缺乏危害的重要阻碍[10]。普遍食盐加碘已被许多国家采用来解决碘缺乏问题。截止到2020 年,全球有124 个国家制定了强制性食盐加碘立法,其中21 个国家制定了允许自愿加碘的立法,普遍食盐加碘方案已被认为是预防碘缺乏有关疾病的最具成本效益的干预措施之一[11-14]。强制性食盐加碘后,多结节性毒性甲状腺肿、单发毒性腺瘤或Graves 病引起的甲状腺毒症减少50%[15]。1994 年以来,普遍食盐加碘在我国预防碘缺乏病中取得显著成效,碘缺乏病病情大幅降低,并得到有效控制。人群碘营养水平渐趋适宜,居民的碘摄入量达到充足状态,处于合理、安全的范围,因此坚持食盐加碘政策对于保护甲状腺的健康是必需的[13,16,17]。但随着盐业体制改革和群众生活水平的提高以及负面舆论的影响,群众对于食用加碘盐存在误解,自愿选择未加碘食盐的人数不断增多,盐业体制改革后食盐加碘防治碘缺乏病工作面临着新的挑战[18]。
根据《中国碘盐监测》(1996-2011)青海省2004-2011 年碘盐监测工作总结,利用2005、2007、2008、2009 和2011 年的数据(2006、2010 年玉树州所辖6 县未进行监测)分别建立非碘盐率、碘盐覆盖率、碘盐合格率及合格碘盐食用率灰色系统理论GM(1,1)模型,之后对上述各指标2012 年情况进行预测。2012 年非碘盐率预测值为1.87%;碘盐覆盖率预测值为98.87%;碘盐合格率预测值为96.99%;合格碘盐食用率预测值为96.07%。由预测值以及数据图形模拟得出非碘盐率理论预测值呈下降趋势,碘盐覆盖率、碘盐合格率以及合格碘盐食用率理论预测值呈上升趋势,说明加碘食盐的推广和普及得到稳步提升,碘盐覆盖面不断扩大,合格碘盐食用率不断增加。可以认为模型预测结果可靠,精度较好,具有科学、准确的预测效果。碘盐干预措施效果是保证人群碘营养水平的指标之一,要保证人群碘营养水平适宜,既要考虑不同人群的碘营养需求,也要参考当前人群的碘营养状况以及变化趋势[16]。如果将灰色系统理论与碘盐监测、人群碘营养监测指标相结合,应用到碘缺乏病预警预测中,充分利用各项监测指标,从理论上推测出碘盐和碘营养等指标的变化趋势,预测未来人群碘营养水平和病情变化,可以及时调整防治策略,指导落实防治措施,继续提高居民健康素养,增强居民合理补碘的意识[17],做到“因地制宜、分类指导、科学补碘”。
综上所述,非碘盐率理论预测值呈下降趋势,碘盐覆盖率、碘盐合格率以及合格碘盐食用率理论预测值呈上升趋势。通过建立灰色系统理论GM(1,1)模型可从理论上预测碘盐相关指标的升降及波动情况,从而及时采取相应措施,指导科学补碘。

