自适应控制中的Hartley块算法及实验*
柴 凯,刘树勇,高伟鹏,朱石坚
(1. 海军工程大学 舰船与海洋学院, 湖北 武汉 430033; 2. 海军工程大学 动力工程学院, 湖北 武汉 430033)
低频线谱直接影响潜艇的安全和制约战斗力的发挥,是潜艇水声隐身性能和战技术性能的主要危害[1]。旋转机械造成的低频线谱表现尤为突出,如何减小机械振动引起的低频辐射噪声是提高潜艇水声隐身性能的关键。目前,潜艇机械设备减振大多采用被动隔振方式,包括单层隔振、浮筏隔振、双层隔振和气囊隔振等,被动隔振对于低频线谱抑制效果并不理想,控制对象突变时可能导致控制失效,缺乏自适应性[2]。主动隔振是在被动隔振基础上引入次级振源,由执行机构产生控制力,控制器采集受控系统的振动特征信号进行滤波,并按照一定控制算法得到控制信号,将其输出至执行机构产生主动控制力抵消原始振动信号,达到减振降噪的目的[3]。相对于被动隔振,主动隔振可以根据受控对象实时响应,及时调整控制信号,对于外界干扰和系统不确定性具有很强的鲁棒性和适应性[4]。
自适应控制算法设计是振动主动控制研究的核心,其性能决定了整个控制系统性能,可分为前馈控制、自校正控制和模型参考控制等[5-6],国内外学者设计了针对不同隔振系统的自适应控制算法。王迎春等解决了自适应算法结构、理论推导、性能分析等问题,针对不同控制系统改进算法,得到了较好控制效果[7]。最小均方(least mean square,LMS)自适应算法,是由Widrow等提出的,以误差信号方差作为目标函数,使控制权系数沿着方差负梯度方向进行迭代,不断逼近最优解的递推算法[8]。Elliott等在研究有源噪声控制时,将LMS算法引入振动控制方面,取得了很好的效果[9]。随后,Burdisso将前馈式主动控制应用到振动控制领域,根据实际控制系统改进LMS算法,较好抑制了结构振动引起的辐射噪声[10]。张玉璘将分解重构LMS算法应用于主动控制系统,提高了算法收敛性和适应性[11]。张强等针对不确定非线性系统的跟踪控制问题,提出自组织小波小脑模型,并将其应用于近空间飞行器姿态控制仿真实验[12]。针对动态变化的离散非线性系统,张晓宇等采用小波包设计智能自适应滑模控制算法,控制系统有较强的鲁棒性[13]。高伟鹏等提出了一种小波包滤波最小均方(wavelet packet filtered-x least mean square,WP-FxLMS)算法,在多频波动激励下,线谱振动能量显著降低[14]。
但WP-FxLMS算法在频带划分后,子频带信号进行运算时包含大量卷积和相关运算,计算量大、收敛速度慢。为此,本文将Hartley块算法应用到WP-FxLMS算法中,提出了基于Hartley块的小波包滤波最小均方(wavelet packet based on Hartley block filtered-x least mean square,WPHB-FxLMS)算法,并通过仿真和实验验证算法的可行性和有效性。
1 子频带中的Hartley块算法
为进一步增大收敛速率,采用块滤波最小均方(block FxLMS,B-FxLMS)算法,使滤波器的自适应更新分块进行。而B-FxLMS算法的关键在于如何实现快速卷积和线性相关运算。Hartley变换为酉变换,仅在实数域内即可完成,且快速Hartley变换在频域内也能实现快速卷积和相关运算,故可采用Hartley变换来实现B-FxLMS算法。
1.1 离散Hartley变换及快速算法
长度为N的实数序列{x(0),x(1),…,x(N-1)}正交变换为Hartley域序列{X(0),X(1),…,X(N-1)}的过程称为离散Hartley变换(discrete Hartley transform,DHT),具体定义[15]为:
(1)
式中,cas(2πux)=cos(2πux)+sin(2πux)。
离散Hartley反变换(inverse discrete Hartley transform,IDHT)定义为:
(2)
同离散Fourier变换(discrete Fourier transform,DFT)性质相似,DHT同样具有快速算法,下面基于快速Fourier变换(fast Fourier transform,FFT)分裂基的思想,推导快速Hartley变换(fast Hartley transform,FHT)实现方式。
若{x(n)}长度N=2m,将信号按奇偶序号分解,然后对奇序号再进行分解得到1个N/2点的{x(2n)}和2个N/4点的{x(4n-1)}和{x(4n+1)}。令G(k)=BDHT[x(2n)],H1(k)=BDHT[x(4n+1)],H2(k)=BDHT[x(4n-1)]。则X(k)可表示为:
(3)
由上述分析可知,N点序列的DHT计算转化为1个N/2点和2个N/4点的DHT计算,附加相应的乘法和加法运算。1个N/2点DHT计算可转化为1个N/4点和2个N/8点的DHT计算,以此类推。16点分裂基的算法流程如图1所示。
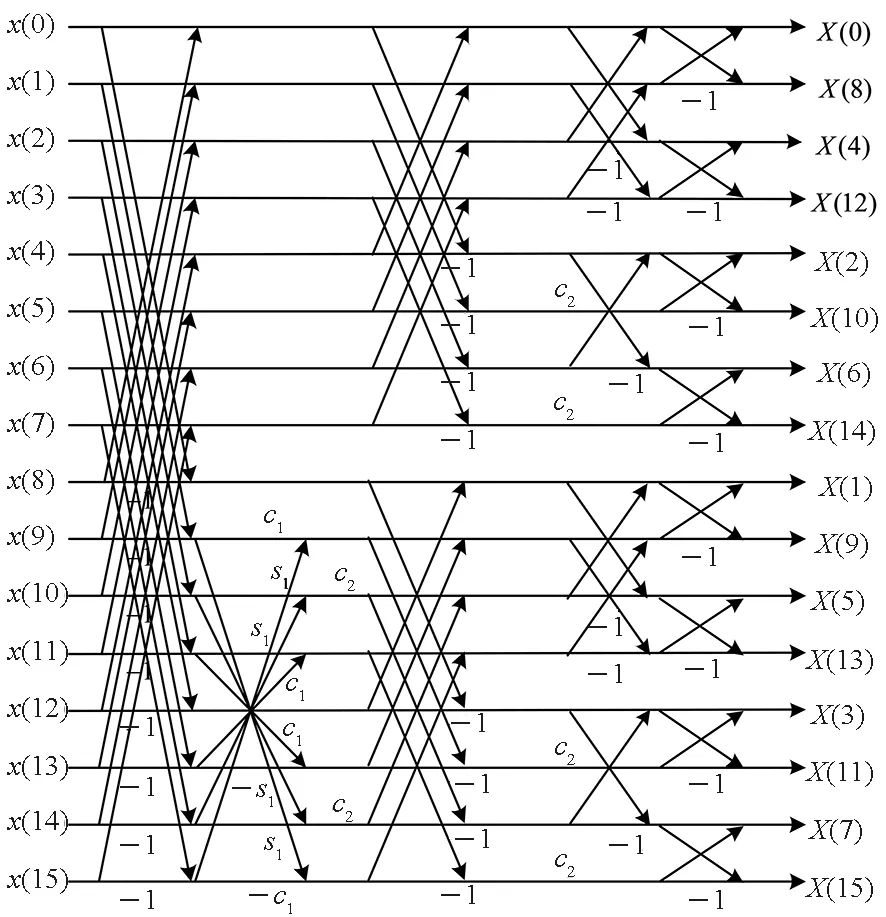
图1 16点分裂基的DHT流程Fig.1 DHT flow diagram of 16 point split-base
为简化计算量可将系数预先计算并存储,以16点分裂基为例,令c1=cos(π/8),s1=sin(π/8),c2=2cos(π/4),可得:
(4)
因此,式(3)可转化为:
(5)
式(5)计算量与D1(k)和D2(k)相关,根据正弦和余弦函数特性,D1(k)和D2(k)分段计算公式为:
(6)
假设cas(2kπ/N)与sin(2kπ/N)已知,通过G(k)、H1(k)、H2(k)求得式(5)所需乘法运算Mn和加法运算An分别为:
(7)
则N点FHT算法所需的乘法和加法总运算量为:
(8)
相比FFT,FHT所需的乘法和加法运算量明显减少,且不涉及复数运算,数值稳定、结构简单、易于工程实现。依据循环卷积定理,由FHT实现实数序列快速卷积运算,具体可表示为:
x1(n)*x2(n)⟺X1H(k)X2He(k)+X1H(N-k)X2Ho(k)
(9)
式中,X1H(k)、X2H(k)分别为实数序列x1(n)和x2(n)的DHT变换,且
(10)
同理,由FHT实现互相关运算,具体可表示为:
x1(n)x2(n)⟺X1H(k)X2Ho(k)+X1H(-k)X2He(k)
(11)
1.2 基于Hartley块的小波包滤波最小均方算法
FxLMS算法是将有限长单位冲激响应(finite impact respondence,FIR)滤波器作为控制器,使用LMS算法进行滤波器参数更新,并对参考信号经次级通道滤波,具体结构如图2所示。而B-FxLMS算法的基本思想如下:控制滤波器权系数更新时,输入数据被一次性加到横向滤波器中,每收集完成一块数据后,更新一次滤波器权系数,块数据输入期间,滤波器权系数保持不变。下面具体阐述基于Hartley块的小波包滤波最小均方算法。
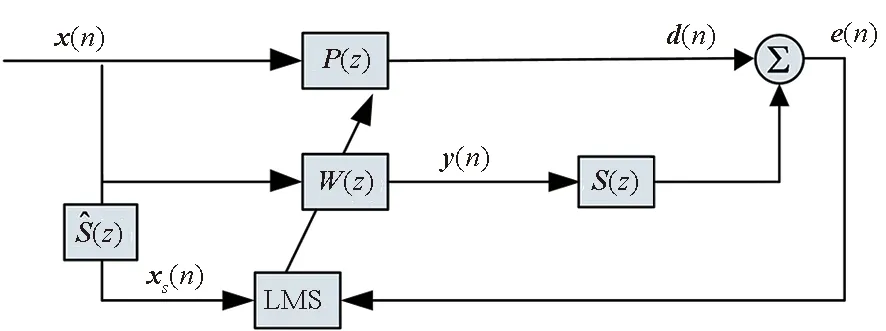
图2 FxLMS算法结构Fig.2 Algorithm structure of FxLMS
将小波包频带划分后的任一子频带分解信号f(n)作为输入数据,将其根据串-并变换器分成P点的块。原采样时刻n,对应第k块、长度为P的数据采样时刻关系为n=kP+i(i=0,1,…,P-1),此时,输入数据由向量变为矩阵:
(12)
数据块输入时,控制滤波器权系数W(k)保持不变。权系数更新只与数据块数k相关,可表示为W(k)=[w0(k),w1(k),…wL-1(k)]T,wj(j=0,1,…,L-1)为每一阶控制器权系数,共L阶。控制滤波器输出定义为:
y(kP+i)=fT(kP+i)W(k)
(13)
次级通道的存在,导致误差信号e(n)由期望信号与经过次级通道滤波的输出信号叠加而成。
e(kP+i)=d(kP+i)+S(z)y(kP+i)
(14)
根据梯度下降原理,采用该数据块所对应各瞬时梯度估计的无偏时间平均作为梯度估计向量,得到滤波器权系数随数据块数k更新的公式为:
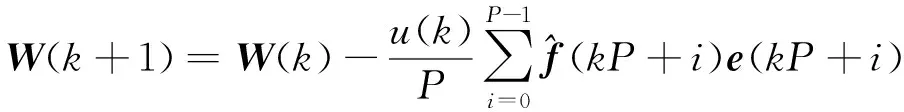
(15)
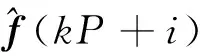
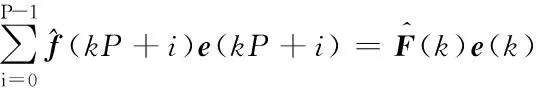
(16)
可见,WPHB-FxLMS算法与WP-FxLMS算法相比,数据输入类型与运算方式没发生根本变化,只是将输入参考信号进行批量处理,且在数据输入期间控制器保持不变,减小了权系数逼近最优解的计算次数,从而提高收敛速率。
对于块数据长度的选择,一般有三种情况:
1)P=L,块长度与滤波器长度保持一致,此时算法具备最简性;
2)P>L,块长度大于滤波器长度,此时梯度向量估计使用过多样本信息,导致冗余计算;
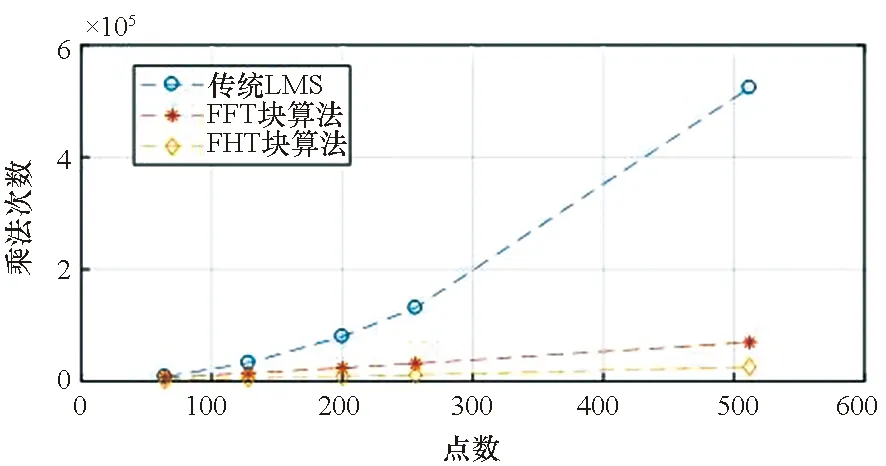
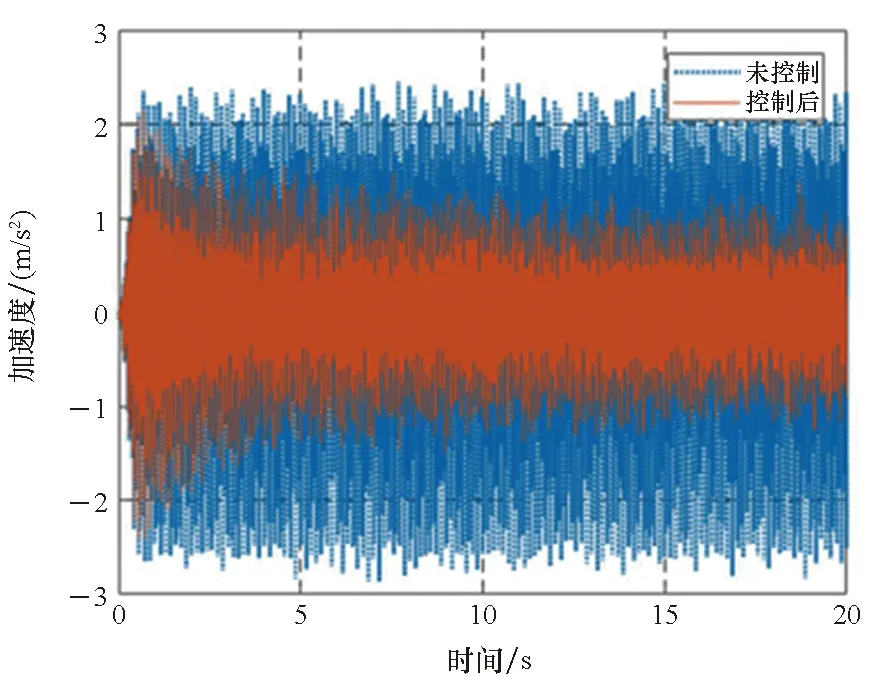
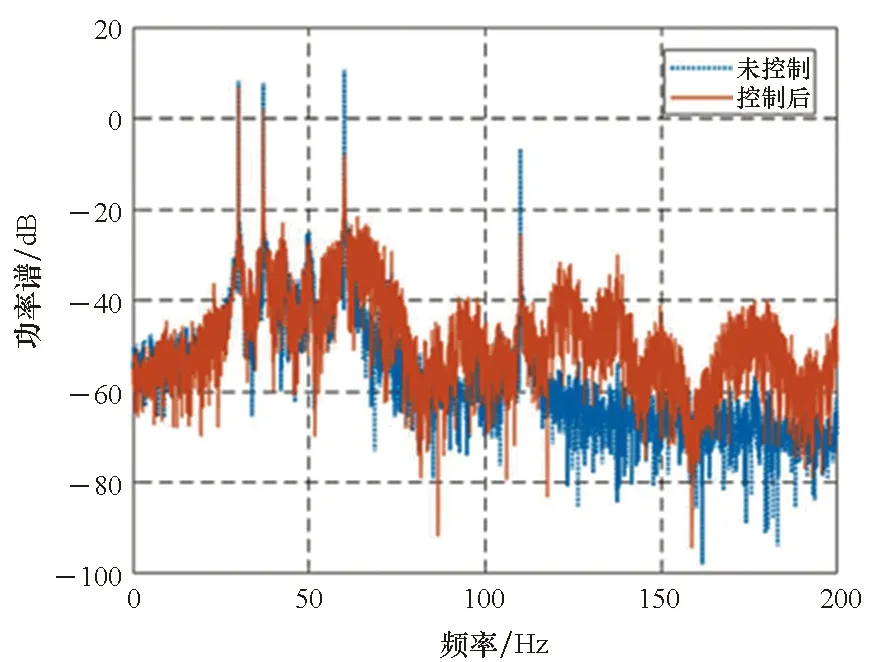
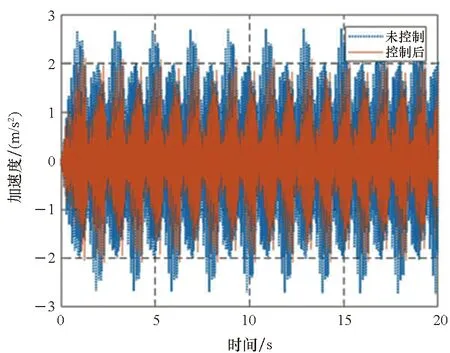
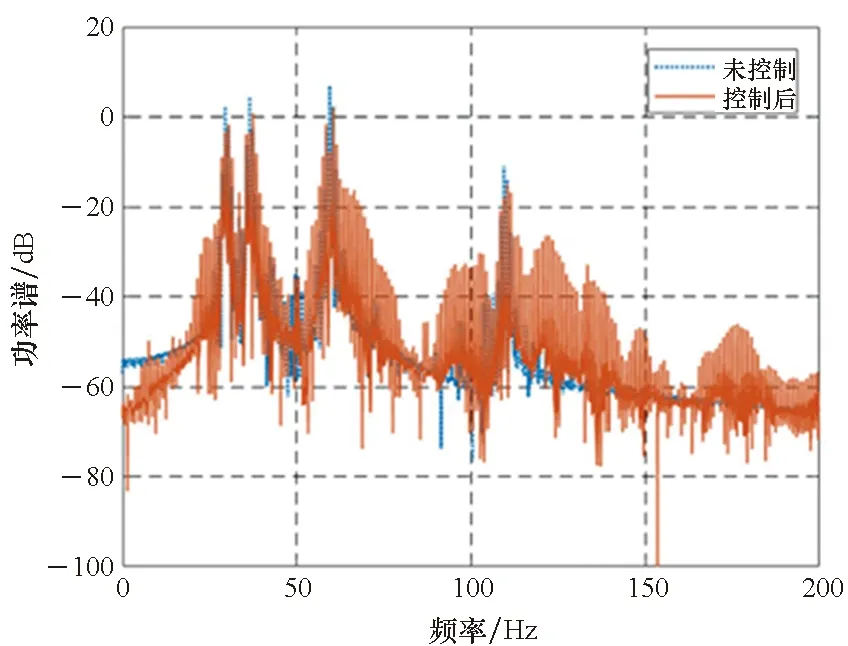
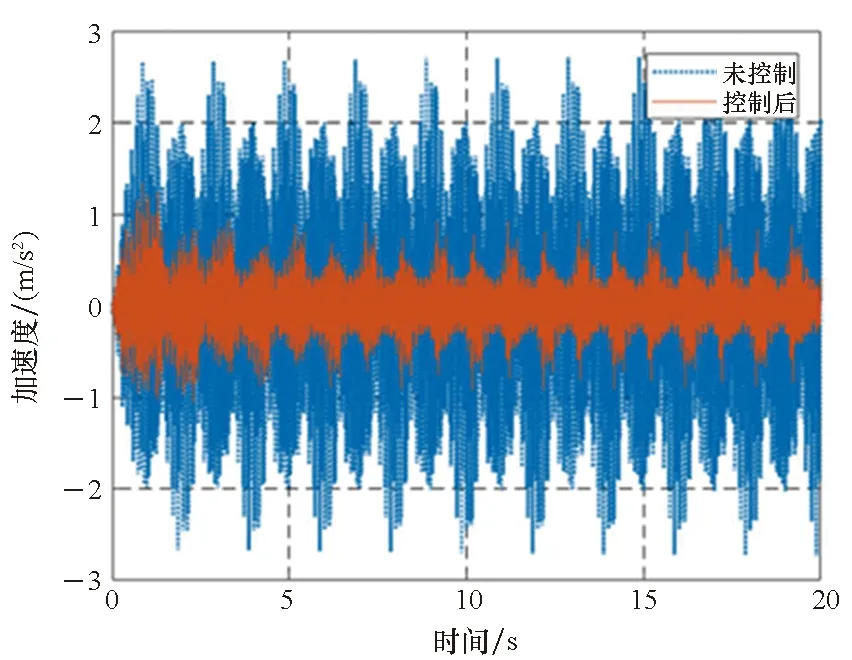
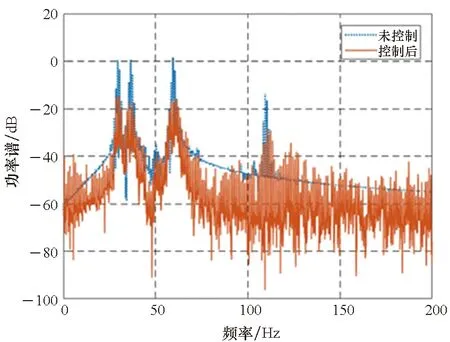
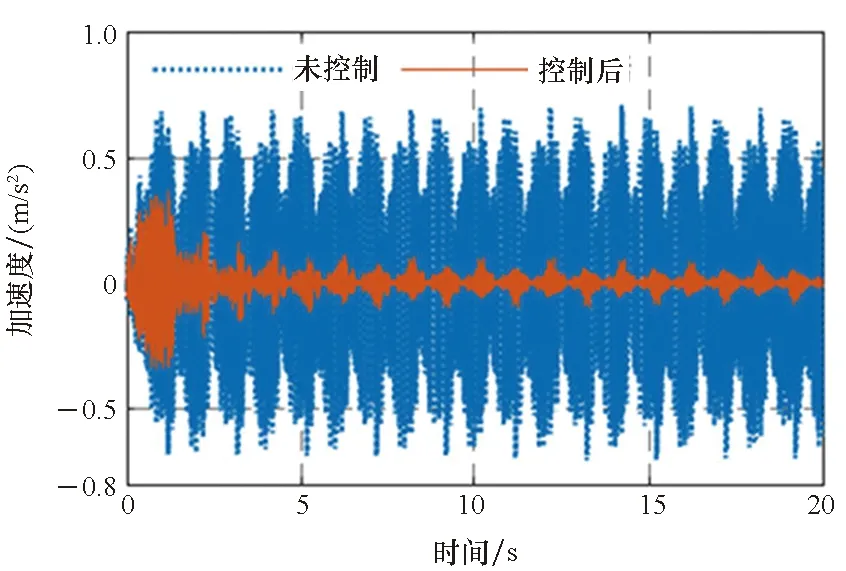
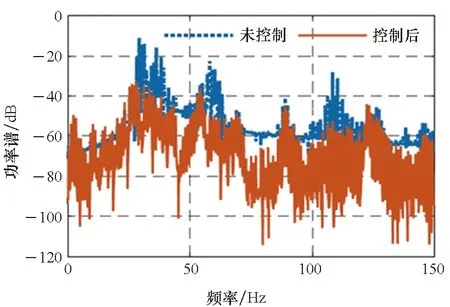
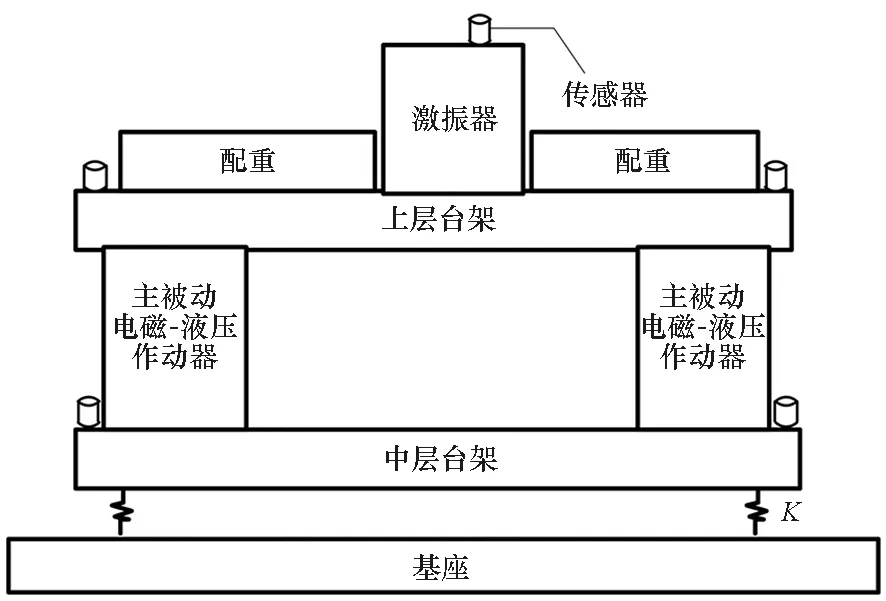
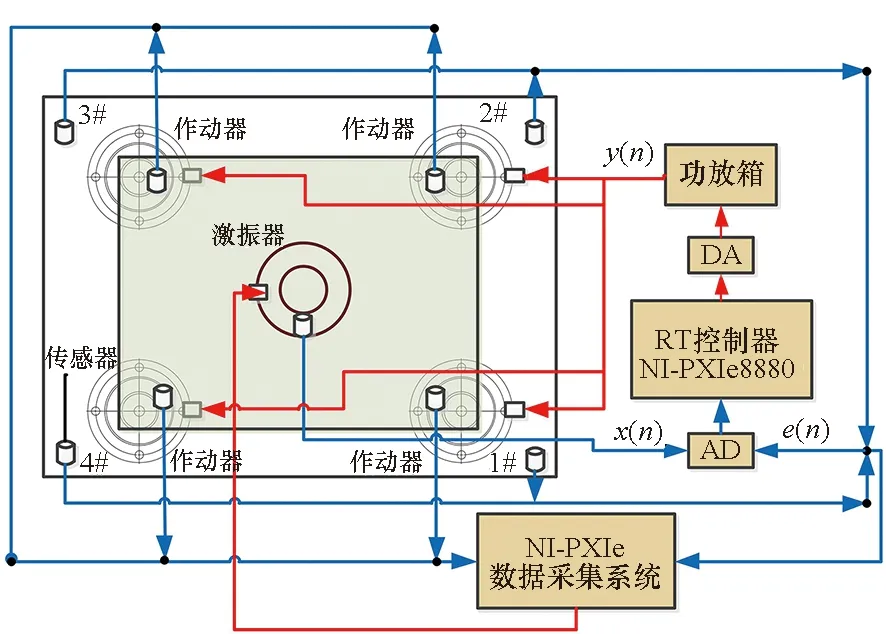
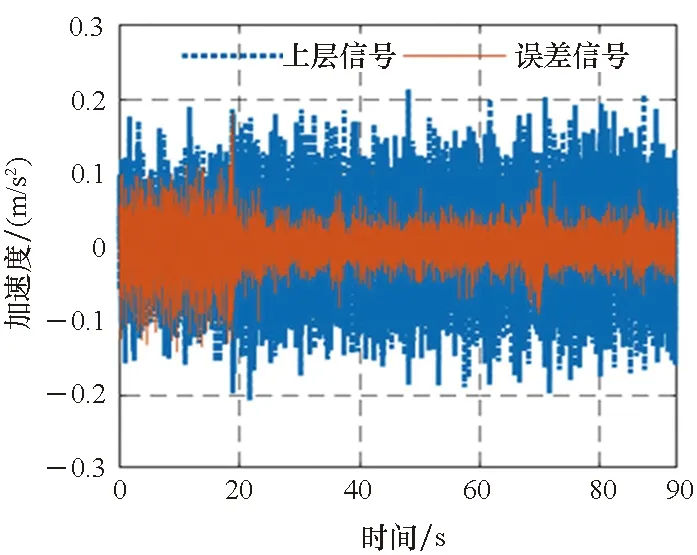
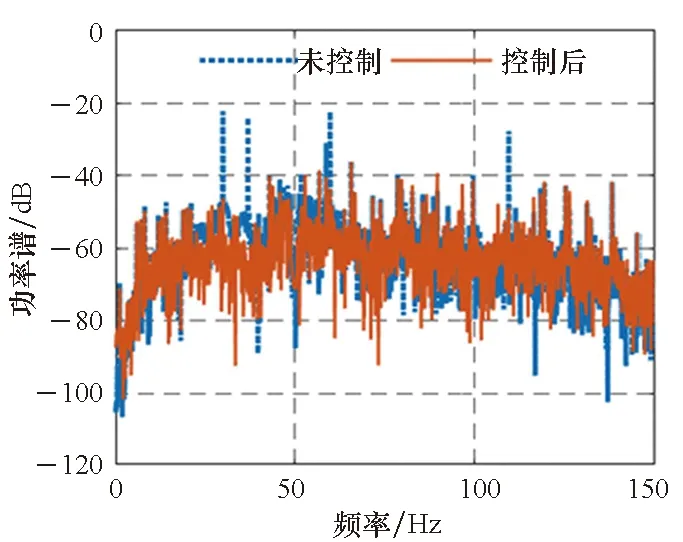
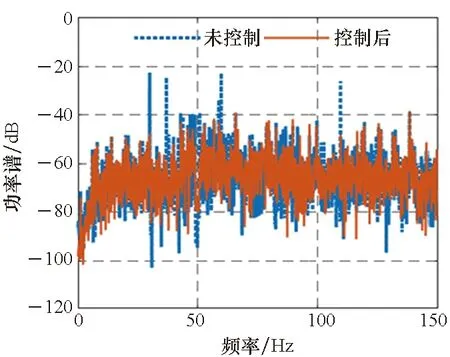
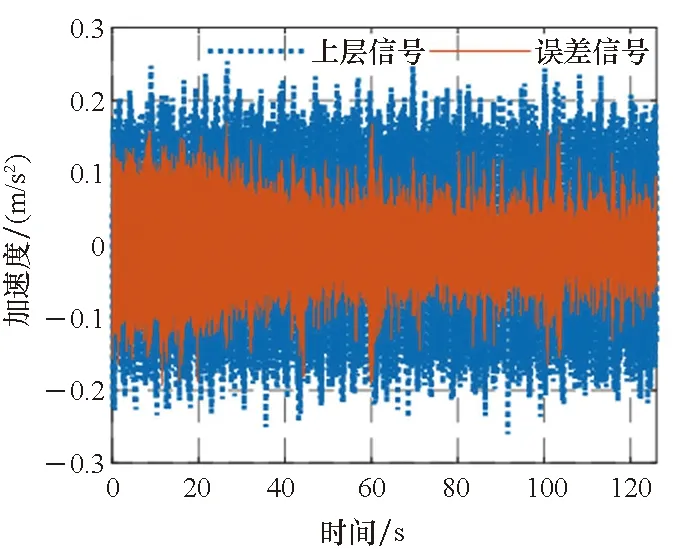
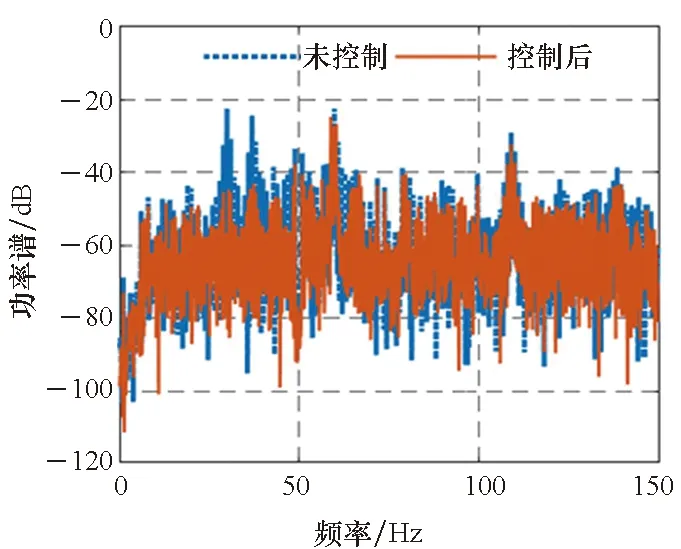
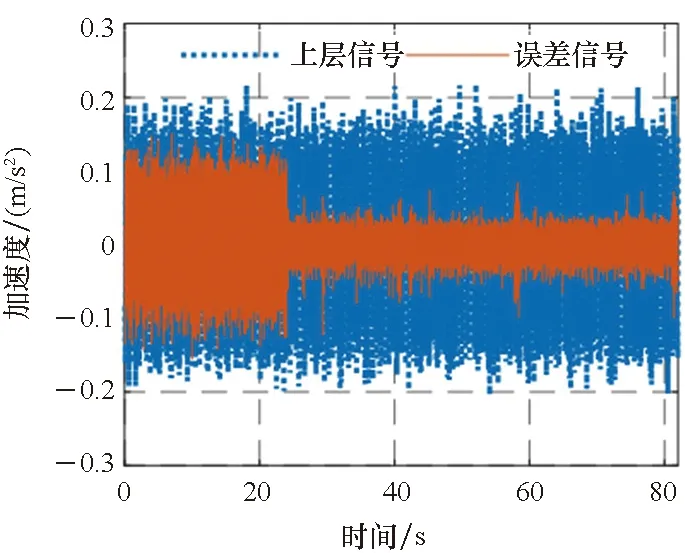
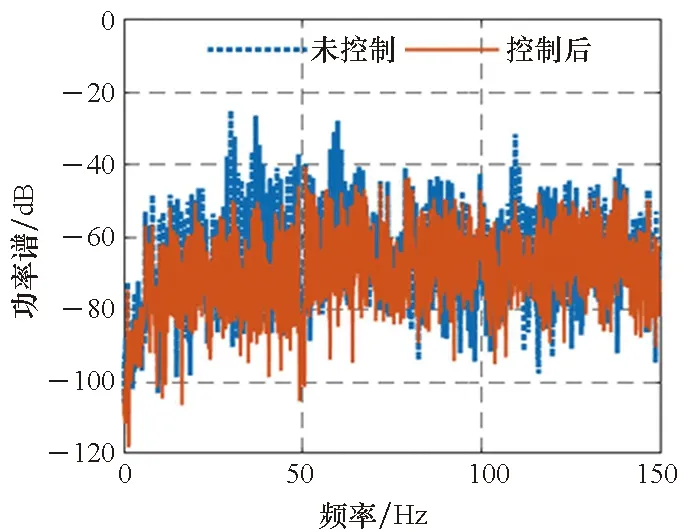
3)P 工程实际中,通常选择P=L分块处理的50%重叠保留法,再通过时滞补偿减小时延对控制系统的影响[16]。将滤波器L个抽头权值用等数的零来填补,并对其进行2L点的FHT变换: (17) 此时,输入数据为2个相继的子块,类型为2L×2L对角矩阵,对其进行FHT变换,得到: (18) 将重叠保留法应用于式(13)的线性卷积,由式(10)可得: (19) 对yH(k)进行逆变换,取后L个点作为第K块数据的输出信号,即y(n)=CIFHT[yH(k)]。 (20) 将重叠保留法应用于式(16)的线性卷积,由式(11)可得: (21) 取ΔW(k)前L个元素作为时域控制权系数的修正项。为与频域权向量长度保持一致,在时域修正项ΔW(k)后面补零,使其总长度为2L,并进行FHT变换,此时,权向量更新Hartley域表达式为: (22) 为便于表示,定义蝶形运算单元如图3所示。 图3 蝶形运算单元Fig.3 Butterfly processor WPHB-FxLMS算法结构如图4所示,细线表示时域内数据流,粗线表示Hartley域内数据流。FHe(k)、FHo(k)分别是由FH(k)构造的偶函数和奇函数。 图4 基于Hartley块的WP-FxLMS算法Fig.4 WP-FxLMS algorithm based on Hartley block 算法的具体数据流程归纳如下: 1)将通过小波包频带划分后的时域连续子频带信号f(n)进行块处理,长度为L,与控制滤波器阶数保持一致,然后级联两个数据块作2L点FHT变换,得到FH(k),分别构造偶函数FHe(k)和奇函数FHo(k),作为Hartley域滤波器输入信号; 2)偶函数FHe(k)和奇函数FHo(k)与频域控制权向量通过蝶形运算,得到频域输出信号yH(k),对其进行IFHT变换,取后L个点作为时域控制输出信号y(n); 3)时域控制信号y(n)经过物理次级通道与期望信号d(n)叠加后,产生误差信号e(n),对其进行块处理并补零,然后通过2L点的FHT变换,得到频域误差信号eH(k),用于更新权系数修正项; 5)对时域内修正项补零后进行2L点的FHT变换,完成Hartley域控制权系数更新。 WPHB-FxLMS算法与WP-FxLMS算法的根本差异在于迭代过程中梯度向量估计方法不同,WPHB-FXLMS算法使用无偏时间平均梯度向量,估计精度会随着数据块长度的增加而提高。假设WPHB-FxLMS算法收敛步长为uB,WP-FxLMS算法步长为u,对WPHB-FxLMS算法进行收敛性分析,得到收敛条件为0 (23) 因此,WPHB-FxLMS算法与WP-FxLMS算法收敛性能基本相同,但是有效步长增大了L倍。 下面,以算法中涉及的乘法运算为基础,对WPHB-FxLMS算法、基于频域块的小波包滤波最小均方(wavelet packet based on frequency-domain block filtered-x least mean square,WPFB-FxLMS)算法与WP-FxLMS算法的计算复杂程度进行对比分析。 假设滤波器长度设为L,对于WP-FxLMS算法而言,权向量更新和控制信号计算所需乘法次数为2L2;而对于WPFB-FxLMS算法,N=2L点的FFT及IFFT所需乘法次数大约为Nlog2N,如图4所示信号流程,需6次时频变换,卷积和相关运算均需4N次乘法,算法总乘法次数为: MFFT=6Nlog2N+8N=12Llog2L+28L (24) =6Llog2L-4L+12 (25) 将滤波器长度分别设为64、128、200、256、512阶,三种算法复杂度对比如图5所示。由图5可知,WPHB-FxLMS算法大大减小了算法复杂度,且长度越大优势越明显。WPHB-FxLMS算法不牵扯复数运算,在每个自适应周期的计算量均少于WPFB-FxLMS算法。L=256时,WPFB-FxLMS算法计算量为31 744,WPHB-FxLMS算法计算量为11 276,而时域内WP-FxLMS算法计算量为11 276。因此,WPHB-FxLMS算法计算量约为WPFB-FxLMS算法的1/3,约为WP-FxLMS算法的1/11,WPHB-FxLMS算法可大大降低计算复杂程度,能更好应用于工程实际。 图5 不同算法的乘法总次数Fig.5 Total multiplication times of different algorithms 初始激励信号为30 Hz、37 Hz、60 Hz、110 Hz四定频信号,叠加信噪比30 dB的零均值高斯白噪声,采样频率为1 kHz,控制器阶数为256。图6、图7和图8是不同控制算法的效果对比图。由图6可知,施加FxLMS算法控制后,控制效果不佳,时域内振动幅值降幅仅35%,控制后60 Hz和110 Hz线谱得到一定控制,而30 Hz和37 Hz线谱基本无控制效果。由图7可知,施加WP-FxLMS算法控制后,振幅降幅达到90%,时域控制效果较好,控制后功率谱衰减较大,线谱特征不再显著。由图8可知,施加WPHB-FxLMS算法控制后,误差信号快速衰减,振幅降幅可达95%,30 Hz、37 Hz、60 Hz、110 Hz线谱功率谱衰减分别为40 dB、42 dB、43 dB、45 dB,控制效果显著,且收敛时间从8 s缩短至2 s,大幅提高了收敛速度,进一步增加了控制精度。 (a) 误差信号时间历程(a) Time history of error signal (b) 误差信号功率谱(b) Power spectrum diagram of error signal图6 定频激励下FxLMS算法的仿真效果Fig.6 Simulative effect of FxLMS algorithms under fixed frequency excitation (a) 误差信号时间历程(a) Time history of error signal (b) 误差信号功率谱(b) Power spectrum diagram of error signal图7 定频激励下WP-FxLMS算法的仿真效果Fig.7 Simulative effect of WP-FxLMS algorithms under fixed frequency excitation (a) 误差信号时间历程(a) Time history of error signal (b) 误差信号功率谱(b) Power spectrum diagram of error signal图8 定频激励下WPHB-FxLMS算法的仿真效果Fig.8 Simulative effect of WPHB-FxLMS algorithms under fixed frequency excitation 初始激励信号为四扫频信号,扫频时间为1 s,频率范围分别为28~31 Hz、35~38 Hz、58~61 Hz、108~111 Hz,叠加信噪比为30 dB的零均值高斯白噪声,模拟机械设备振动频率小范围快速波动时的工况。图9、图10和图11是不同控制算法的效果对比。由图9可知,FxLMS算法控制后,振幅降幅仅为15%,四个扫频段内功率谱控制后几乎无衰减。由图10可知,施加WP-FxLMS算法控制后,扫频线谱得到较为快速而有效的控制,振幅降幅达到85%,功率谱能量衰减明显,线谱特征不再显著。由图11可知,施加WP-FxLMS算法控制后,振幅降幅达90%,28~31 Hz、35~38 Hz、58~61 Hz、108~111 Hz扫频段功率谱衰减分别为26 dB、28 dB、28 dB、25 dB,控制效果显著,而且收敛时间从9 s缩短至2 s,进一步提高了控制精度,证明了算法的有效性。 (a) 误差信号时间历程(a) Time history of error signal (b) 误差信号功率谱(b) Power spectrum diagram of error signal图9 扫频激励下FxLMS算法的仿真效果Fig.9 Simulative effect of FxLMS algorithms under fluctuant frequency excitation (a) 误差信号时间历程(a) Time history of error signal (b) 误差信号功率谱(b) Power spectrum diagram of error signal图10 扫频激励下WP-FxLMS算法的仿真效果Fig.10 Simulative effect of WP-FxLMS algorithms under fluctuant frequency excitation (a) 误差信号时间历程(a) Time history of error signal (b) 误差信号功率谱(b) Power spectrum diagram of error signal图11 扫频激励下WP-FxLMS算法的仿真效果Fig.11 Simulative effect of WP-FxLMS algorithms under fluctuant frequency excitation 以激振器作为隔振对象,模拟舰船机械设备振动状态并进行主动控制实验。将自主研制的电磁橡胶液压主被动混合隔振器作为执行结构,结合实时性好、计算能力强的NI-PXIe测控硬件搭建双层隔振实验系统,来验证WPHB-FxLMS算法的有效性。 双层隔振实验台架框图及各部分安装位置如图12所示。将激振器作为振源安装在台架上层,同时安装质量块作为配重增大隔振器总支承重量,将振源产生的加速度信号作为整个系统的参考信号。中层台架四角位置处各放置一个电磁橡胶液压主被动一体化隔振器,作为次级振源,与上下台架均通过螺栓连接,上下连接处附近位置安装加速度传感器,上层传感器作为监测信号,下层传感器作为误差信号,通过上下层加速度信号可直观得到隔振效果。中层台架通过弹性支架与基座连接,动力学特性可简化为弹簧阻尼结构。 图12 双层隔振台架框图及安装情况Fig.12 Block diagram of double-layer vibration isolation platform and installation 图13为控制系统示意图,蓝线为信号采集过程,红线代表信号输出过程。加速度传感器采集参考信号和误差信号,经输入板卡至实时(real-time,RT)控制器,通过控制算法得到四个控制信号,经输出板卡至功率放大器,驱动隔振器产生控制力,减小振动向基座传播,进行主动控制实验的同时,采用另一套NI-PXIe驱动上层激振器,同时采集上层台架和中层台架所有加速度信号,用于实时监测和后续数据处理。 图13 隔振实验台架控制系统Fig.13 Control system of vibration isolation test bench 将次级通道估计放入控制系统中,进行主动控制实验。为逼近柴油机运行状态下线谱频率成分,分两种工况进行实验:第一,将激振器激励信号设置为频率为30 Hz、37 Hz、60 Hz、110 Hz正弦线谱激励;第二,将参考信号设置为周期为1 s,频率变化范围为28~31 Hz、35~38 Hz、58~61 Hz、108~111 Hz四个扫频Chirp信号。叠加30~60 Hz幅值为0.1 A的白噪声,采样频率为1 kHz,四通道输出电压幅值|y|<9 V,控制器阶数为256,对所有采集信号使用3阶巴特沃思滤波进行200 Hz低通滤波。具体实验步骤如下: 1)将激励信号通过PXI-6733输出至功放,驱动激振器产生参考信号,待振动稳定后,开启数据采集系统,采集上层信号和误差信号,观察隔振效果; 2)设置各个控制回路初始迭代步长(根据经验公式修正),开启控制,待误差信号收敛稳定后,关闭控制系统和数据采集系统; 3)采集信号进行数据处理,将每个测点所对应的上层信号和误差信号放在同一时间历程图中,时域图上体现控制前被动隔振效果和控制后的收敛性能、控制精度等。对控制前后误差信号各取10 000个点进行功率谱分析,以误差信号控制前后功率谱衰减量作为隔振评价指标。 对参考信号和误差信号进行小波包分解,分解层数为5,基函数为“dmey”小波基,在小波包分解基础上,在子频带内使用Hartley域块控制策略。图14和图15表示定频激励下不同控制方法1#测点误差信号时间历程图和控制前后功率谱。由图14可知,采用WP-FxLMS算法,第19 s开启主动控制,误差信号衰减较快,最大降幅可达81%,在第32 s时控制基本稳定,收敛时间为13 s,四根线谱得到有效抑制,最大线谱衰减可达30 dB,且未激起其他线谱振动,控制效果良好。由图15可知,采用WPHB-FxLMS算法,第23 s开 (a) 误差信号时间历程(a) Time history of error signal (b) 误差信号功率谱(b) Power spectrum diagram of error signal图14 定频激励下WP-FxLMS算法的实验效果Fig.14 Experimental effect of WP-FxLMS algorithms under fixed frequency excitation (a) 误差信号时间历程(a) Time history of error signal (b) 误差信号功率谱(b) Power spectrum diagram of error signal图15 定频激励下WPHB-FxLMS算法的实验效果Fig.15 Experimental effect of WPHB-FxLMS algorithms under fixed frequency excitation 启主动控制,第25.5 s完成收敛,收敛速度大大提高,最大降幅可达85%,四根线谱得到有效抑制,控制之后线谱特征基本淹没于背景噪声之中,且未激起其他频率的振荡。 图16和图17表示扫频激励下不同控制方法1#测点误差信号时间历程图和控制前后功率谱。由图16可知,采用WP-FxLMS算法,第18 s开启主动控制,在第36 s时控制基本稳定,收敛时长为16 s。在每个测点处,四根线谱都得到有效抑制,线谱平均衰减达20 dB,且未激起其他线谱振动,控制效果良好。由图17可知,采用WPHB-FxLMS算法,第24 s开启主动控制,第25.5 s完成收敛,收敛速度极快,控制后误差信号降幅最高可达86%,四个测点处扫频线谱功率谱衰减明显,控制之后线谱信号基本淹没于背景噪声之中,且未激起其他频率振荡。 (a) 误差信号时间历程(a) Time history of error signal (b) 误差信号功率谱(b) Power spectrum diagram of error signal图16 扫频激励下WP-FxLMS算法的实验效果Fig.16 Experimental effect of WP-FxLMS algorithms under fluctuant frequency excitation (a) 误差信号时间历程(a) Time history of error signal (b) 误差信号功率谱(b) Power spectrum diagram of error signal图17 扫频激励下WPHB-FxLMS算法的实验效果Fig.17 Experimental effect of WPHB-FxLMS algorithms under fluctuant frequency excitation 本文针对时域算法收敛速度慢,控制信号计算包含大量卷积和相关运算等问题,使用Hartley块运算生成子频带控制信号,提出了WPHB-FxLMS算法。主要工作和结论总结如下: 1)将FHT变换引入块算法中,可实现频域内快速卷积和相关运算,在实数域内即可完成信号处理,大大减小了时频转换计算量; 2)基于WP-FXLMS算法基础,在子频带内引入Hartley域块算法,通过重叠保留法具体实现,提出了WPHB-FxLMS算法,可使收敛速度加快,计算复杂度显著降低,控制精度也得到了提高; 3)仿真和实验结果表明,WPHB-FxLMS算法对于多定频激励和扫频激励两种工况均有显著控制效果和快速收敛性。
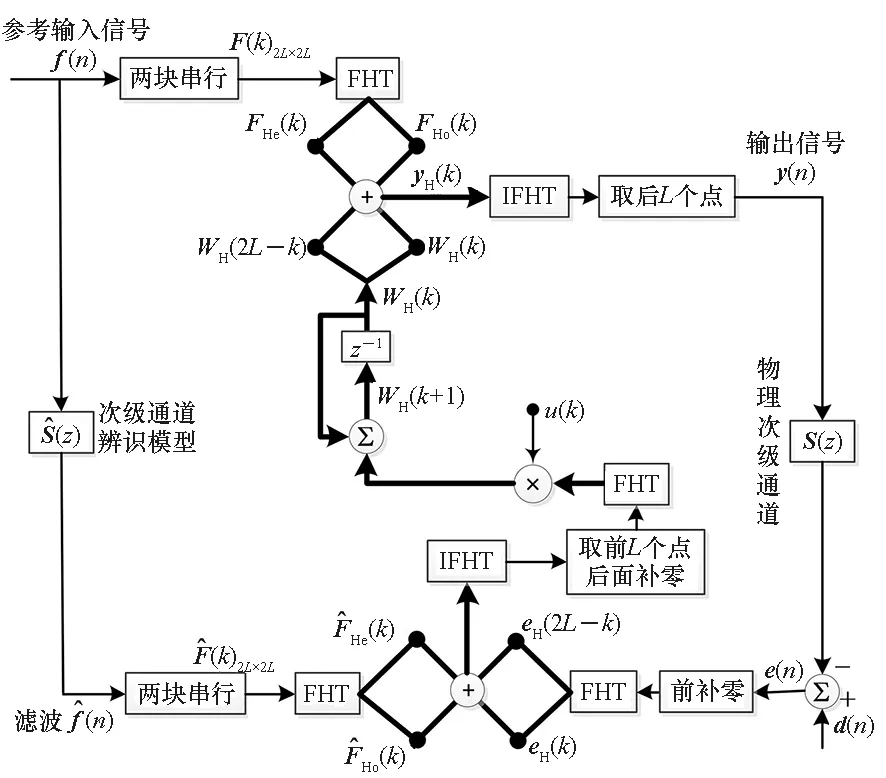
1.3 WPHB-FxLMS算法的特性分析
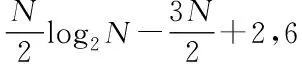
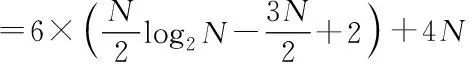
2 仿真研究
2.1 定频线谱控制
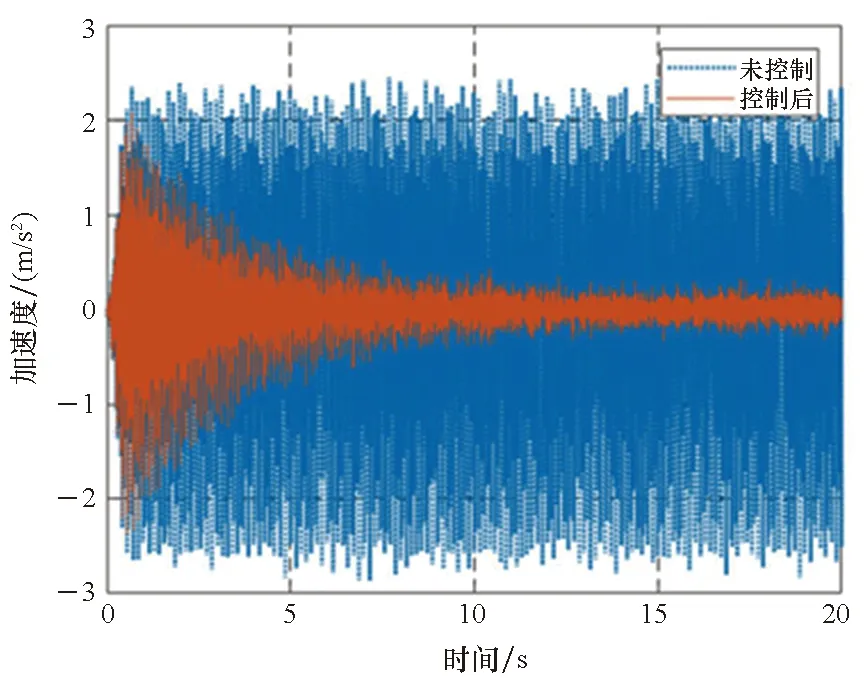
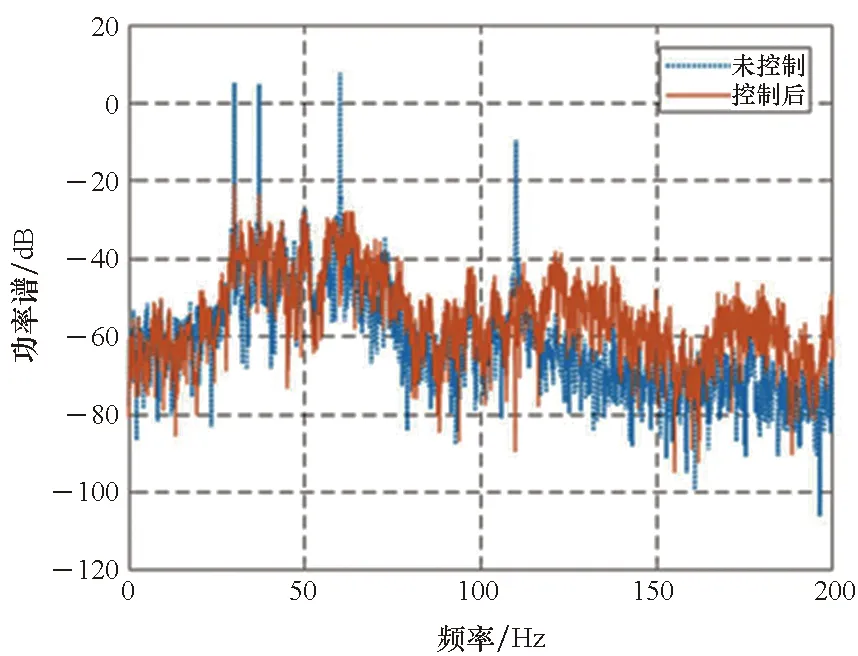
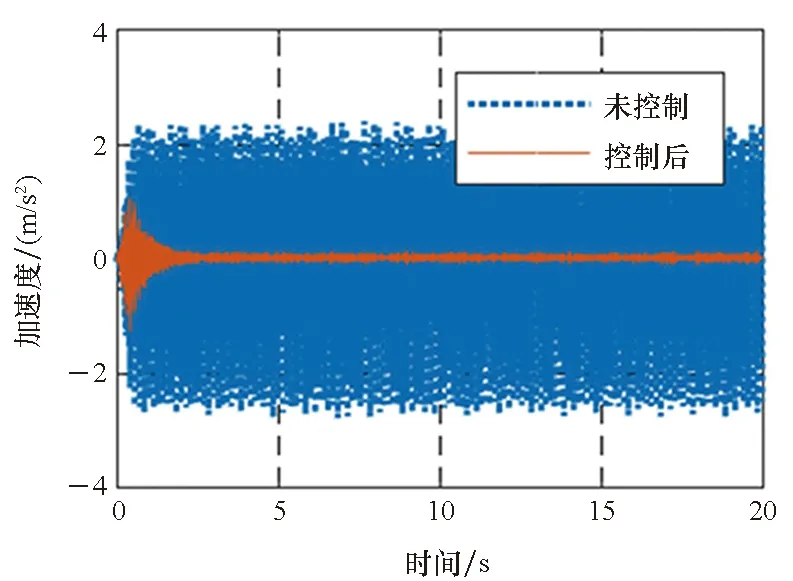
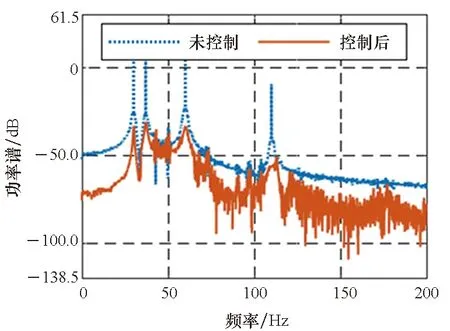
2.2 扫频线谱控制
3 实验研究
3.1 实验台架的搭建
3.2 实验步骤和结果分析

4 结论

