基于多目标模糊规划的海上要地防空动态火力分配

赵文飞, 刘孝磊, 马翠玲, 滕克难

(海军航空大学航空基础学院, 山东 烟台 264001)

0 引 言

随着信息化、网络化技术的快速发展,现代防空反导作战体系为多类型防空武器平台联合的“一体化协同作战模式”[1],各平台的预警系统、指挥控制系统、雷达火控系统等联成网络,实现战场态势一张图,统一协同防空反导作战。其中,多平台协同防空武器火力分配(weapon target assignment, WTA)是“一体化协同作战模式”的关键环节,其主要目的是将不同平台的防空火力作战单元科学合理地分配给不同的来袭目标,以提高整体的防空反导作战效能[2]。以海上要地防空为例,海上要地防御纵深大、区域广、战场环境复杂,主要作战样式为多方向、多梯次、多形式的饱和攻击,而防空反导作战机会稍纵即逝,因此如何快速、有效地实现远、中、近程不同类型的防空WTA是一个非常复杂而又重要的研究领域。鉴于此,本文研究多平台防空武器协同WTA问题。

WTA问题是反导指控系统的核心模块,属于非线性组合优化问题,也是典型的NP(non-deterministic polynomial)完全问题[3]。从作战时间角度出发,Manne[4]首次将WTA问题分为静态WTA(static WTA, SWTA)和动态WTA(dynamic WTA, DTWA)。SWTA是在所有武器同时分配给来袭目标的基础上建立的模型,该模型一直是文献研究的热点。DTWA在SWTA模型的基础上,注重考虑分配过程中可能发生的随机事件并及时处理,研究动态防御作战过程中武器目标的最优分配。自从Farina等[5-6]于2003年第一次提出动态多目标优化问题(dynamic multi-objective optimization problems, DMOPs)之后,有大量的学者投入该问题的研究。目前,关于DTWA的研究主要集中在DMOPs求解算法方面。Zou等[7]提出了基于动态进化环境模型的多目标进化算法。Pan等[8]提出了非合作博弈的对抗WTA模型,并利用分解协同进化算法进行求解。文献[9-10]分别提出了利用非支配排序遗传算法Ⅱ(non-dominated sorting genetic algorithm Ⅱ, NSGA Ⅱ)和NSGAⅢ求解DMOPs问题,实验数据表明了算法在求解该问题时收敛效果较好。

事实上,上述文献大多基于确定性的WTA模型,没有考虑战场环境下的不确定因素,如战场气候、来袭目标的威胁程度、武器系统的杀伤概率等,往往都是不确定的。因此,在实际战场环境中,研究带模糊约束的DWTA问题是一件很有意义的工作。文献[11]提出了静态模糊多目标规划WTA模型,研究了利用多目标粒子群优化算法求解该问题。文献[12]构建了基于模糊约束的双层规划WTA模型。Li等[13-14]分别利用基于自适应权重调整分解的多目标进化算法和ε-约束框架下基于分解的多目标进化算法求解了模糊多阶段多目标WTA模型,有效提高了该问题的收敛速度。由于海上要地防空反导面临诸多不确定因素,战场态势具有高度复杂性和动态性特征,防空武器WTA问题对优化算法的时间性能和收敛性能具有较高的要求。为此,在上述文献研究的基础之上,本文以海上要地防空反导为背景,构建模糊动态WTA(dynamic WTA, DWTA)模型,提出基于NSGA Ⅱ和多目标量子遗传算法(multi-objective quantum genetic algorithm, MOQGA)的多目标优化算法(简称为NS-MOQGA)。经仿真实验表明,NS-MOQGA具有较好的收敛效果。

1 不确定环境下DWTA模型

1.1 确定型DWTA

海上要地一般远离大陆,位置分散,自然环境恶劣,装备与后勤补给困难,且要地配置的防空兵力有限,缺乏地域防御纵深。因此,受地理条件和兵力限制,难以利用要地自身配备的防御系统和兵力构建纵深大的防御体系。为扩展海上要地防御纵深,本文考虑由岸基航空兵前置抗击、水面舰艇中/近程拦截、要地防御兵力末端防御、火炮抗击等形成的远中近、高中低多层次、多兵种海上要地防御体系,如图1所示。

图1 海上要地多层防御体系示意图Fig.1 Schematic diagram of multi-layer defense system in strategic location on the sea

实际上,战时整个海上要地远中近、高中低防御体系在作战过程中是相互交织的,杀伤区域有重叠的现象,很难刻画整个防御过程各个防空平台火力单元的分配问题。因此,为了有效构建海上要地火力分配模型,本文做出以下假设:

(1) 假设某海上要地面临多方向、多角度、多批次的饱和攻击;

(2) 假设某海上要地防御体系由K层防线构成,每层防线可由不同类型的防御武器构成;

(3) 假设我方采取的射击模式为“射击-观察-射击”模式;

(4) 海上要地防御作战过程为由远至近、由高到低梯次展开拦截;

(5) 假设海上要地各层防线武器平台火力控制数据链是通畅的,能够做到“战场态势一张图、指挥一张网”;

(6) 假设在t时刻,该要地防御体系内共有m个不同类型的防空反导武器参与作战,检测到n个来袭目标,其中第i个防空武器平台共有wi枚拦截弹。

通过以上描述,本文根据敌方来袭目标批次和我方多层防御体系以及射击模式,根据t时刻的战场态势,将t时刻之后的拦截过程按远中近、高中低作战防线分为K层防线,如图2所示。

图2 多层防线WTA决策过程Fig.2 Multi-stage WTA decision process

图2中,m(k),n(k)分别为第k层防线防空系统武器和来袭目标的数量。每层防线可视为SWTA。在第k层防线中,假设pij(k)表示第i个防空武器平台装配导弹对第j个来袭目标的杀伤概率,其中i=1,2,…,m(k);j=1,2,…,n(k);第j个目标对海上要地的威胁系数为vj(k);变量xij(k)表示第k层防线第i个武器平台防御第j个目标发射的导弹数量;cij(k)为第k层防线第i个武器平台射击第j个来袭目标的费效比,则第k层防线海上要地的防御效率和拦截损耗分别为

在海上要地动态防御作战过程中,指挥员可根据当前实时的拦截效率和损耗情况,以每层防御效率和拦截损耗的总和为目标函数,制定最优WTA方案。因此,以海上要地在整个防御作战过程中防御效率最大和拦截损耗最小为目标建立的WTA多目标优化模型如下:

(1)

(2)

式中:X=[xij(k)]为各层防线决策变量,确定性火力分配模型的约束条件如下。

C1:在第k层防线火力分配中,最多有wj(k)枚拦截弹用于拦截来袭目标j,即

C2:在第k层防线火力分配中,第i个武器平台拦截的来袭目标数量小于ni(k),即

C3:为每个来袭目标至少分配1个防空武器平台,即

C4:可行约束条件为:

i∈{1,2,…,m(k)};j∈{1,2,…,n(k)};k∈{1,2,…,K}

1.2 不确定型DWTA

海上要地防空反导作战方式本质上是多武器、多目标在复杂环境下的高速动态对抗行动,涉及到信息、决策、武器等多个分系统,具有空天地一体、信息与火力一体的突出特点,使得空袭战术具备较强的多变性和欺骗性,从而让防御指挥决策面临诸多复杂、不确定性因素的考验。不确定性可用随机、模糊数、粗糙集等[15]方式来刻画。本文主要利用模糊数来刻画WTA问题中的不确定性因素。主要包括以下两个方面。

(1) 模糊武器单发杀伤概率。防空武器单发杀伤概率是评估其防空作战能力的重要指标。在一般的WTA计算中,往往以一个确定的数值来刻画单发武器的杀伤概率,但现代防空武器系统杀伤空域较大,在不同的拦截点,其单发武器杀伤概率相差较大,并且在射击过程中还受传感器、装备故障等因素的影响,因此将杀伤概率视为一个确定的数值,显然不够合理。本文受文献[16]的启发,采用梯形模糊数来刻画武器单发杀伤概率:

式中:ξ为随机变量取值,与作战态势、天气条件等有关,取值时可利用不同环境中武器效率的历史观测值,或使用随机模拟数据、专家意见等方式获得,ξi(i=1,2,3,4)为初始值。

(2) 模糊威胁程度系数。不同来袭目标对防御方的威胁程度是不一样的,因此目标识别在威胁程度分析中至关重要,是拦截来袭目标的先决条件。来袭目标在突防过程中往往伴随着电子干扰、诱饵释放等突防技术手段,同时海上要地战场环境复杂,海杂波、气候等都会给来袭目标识别带来不同程度的影响,使得目标的威胁程度具有较强的不确定性。因此,本文将目标的威胁程度视为一个三角模糊数,记为

综上分析,可以给出不确定环境下,DWTA多目标优化模型如下:

s.t. C1, C2, C3, C4

(3)

1.3 确定性等价形式及线性化

第1.2节将不确定环境下的DWTA问题转化为一个模糊的多目标非线性规划问题,目标函数含有模糊数,且是非线性的,从而给式(3)的求解带来了一定困难。下面通过一定的数学方法将模糊数转化为确定性等价形式,把非线性转化为线性函数进行处理。

1.3.1 模糊数等价清晰化

将模糊规划问题转化为确定等价形式优化问题的方法主要包括可信性测度、置信水平、期望值法等[17]。文献[18-19]分别利用模糊运算和效用函数将模糊约束转化为清晰的等价形式进行处理。文献[20]利用隶属函数,给出了三角模糊数取值区间的期望值和取值的期望值。根据文献[20]提出的较为简洁、合理的方法,本文利用期望值法将模糊威胁程度系数等价刻画为确定型数值。

(4)

1.3.2 DWTA线性化

记zj(k)=-lnyj(k),则

从而,式(4)可转化为

(5)

式中:Z=[zj(k)]。

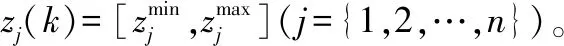
yj(k)=

(6)

从而将目标F1(Z)转化为一个线性函数。

2 算法设计与求解

通过前面的处理,将带模糊约束的非线性多目标优化问题转化为线性的确定性约束的多目标优化问题。针对该问题,本文提出NS-MOQGA,该算法利用量子位概率交叉、经变异保持种群多样性的同时,引入非支配排序、稳定值函数对个体进行优劣分级,采取精英保留策略保持种群的优劣性,提高算法的搜索效率,并与NSGA-Ⅱ算法、MOQGA算法进行比较[21-22],仿真结果表明本文算法的有效性。

2.1 量子比特与量子个体

量子比特是量子信息的基本存储单元,在量子计算中,用量子比特来表示信息,采用|0〉和|1〉表示微观粒子的两种基本状态。量子比特的状态除了|0〉和|1〉,还有叠加态,叠加态处于这两种基本状态之间的中间状态,即

|φ〉=α|0〉+β|1〉

式中:α和β是一对复数,表示量子态的概率幅,即量子态|φ〉以概率α2坍缩到|0〉,以概率β2坍缩到|1〉,且满足|α|2+|β|2=1。

在量子优化算法中,量子个体由量子比特组成串:

式中:量子个体Q由m个量子比特组成;[αi,βi]T为第i个量子的概率幅(|αi|2+|βi|2=1,i=1,2,…,m),一个长度为m的个体可以表示2m个不同的状态。

2.2 染色体编码

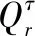
2.3 非支配排序

第1节构建的WTA模型包括防御效率最大和拦截损耗最小两个优化目标,每一个可行解都有两个评价指标,属于多目标优化问题。考虑到多目标的不可共度性,本文引入非支配排序和稳定值来区分解的优劣程度。

种群中每个个体x都设有两个参数xrank和xwd。其中,xrank为非支配排序,根据种群中每个个体的目标函数进行Pareto支配排序[23]。将个体分为0,1,2,…个等级,同一个等级非支配排序相等,非支配排序越低的个体越优秀。xwd为稳定值,表示将各层防线火力通道连续分配给同一目标的次数。由于在实际防空反导过程中,若采取“射击-观察-射击”的模式,在来袭目标没有被击毁的情况下,原则上分配给该目标的火力通道尽量不要改变,以增加射击的稳定性,从而xwd越高,个体越优秀。

2.4 染色体的更新

旋转门是更新染色体的关键环节,量子旋转门的公式如下:

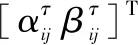
从而旋转角度为

2.5 量子交叉与变异

为了增加种群的多样性,提高算法的收敛速度,在量子进化过程中引入量子交叉与变异。具体过程为:在第τ代种群中,按照预设的交叉概率pc,随机选择若干个体,随机选择量子位相互交叉,产生第τ+1代个体;量子变异过程为在τ代种群中,按照预设的变异概率py,随机选择若干个体,随机选择一定数量的量子位,将这些位置的量子概率幅互换。

2.6 精英保留策略

种群中的个体可通过非支配排序和稳定值来进行排序,为了使每代种群中的优秀个体能够直接进入下一代,本文采用精英保留策略。具体操作为:将父代种群Qτ和子代种群Pτ组合成新的种群Rτ,Rτ=Qτ∪Pτ。计算Rτ中每个个体的非支配排序和稳定值,进行非劣前沿分级,选择满足种群个数的最优个体作为第τ+1代父代种群Qτ+1。

2.7 算法流程图

完整的算法流程如图3所示。

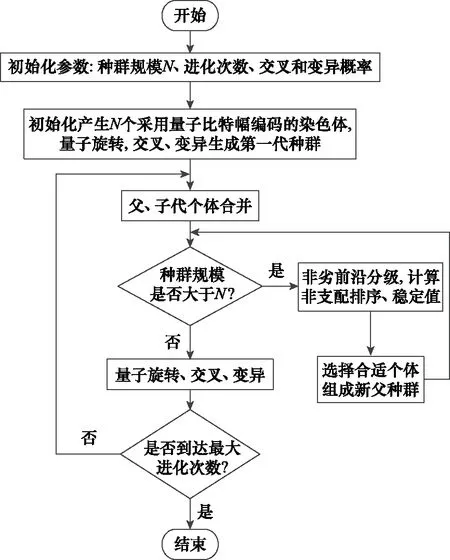
图3 算法流程图Fig.3 Algorithm flow chart

3 实例仿真

3.1 仿真设定

本文以海上要地防空反导为仿真实例,参考文献[10-14]给出的仿真数据,利用随机模拟的方法给出相关参数。假设某海上要地防空分为远、中、近程3层防线,拦截同类型的来袭目标,每层防线防空火力通道数、来袭目标数及相关武器装备参数如表1所示。表1中的拦截概率为梯度模糊数,毁伤效能系数为三角模糊数,其中拦截费效比为给定值附近的随机数,算法中的其他相关参数如表2所示。

表1 某海上要地防空反导相关参数

表2 算法相关参数

根据以上实验数据,利用本文提出的NS-MOQGA算法,与NSGAⅡ算法和MOQGA算法进行仿真对比,仿真环境为CPU:i7-6500U,8.0GB RAM, 2.50 GHz, 操作系统为Windows7,仿真实验工具为MatlabR2018a。

3.2 仿真结果分析

针对NS-MOQGA算法、NSGAⅡ算法和MOQGA算法,本文独立进行了4组随机模拟实验,每组实验进行50次取均值,实验数据如表3和表4所示。表3是在重复实验结果中择优选择的一组分配方案,对照表3,每类武器都被合理地分配了相应的来袭目标,没有出现超出武器数量的约束;每个来袭目标均被拦截了2次,增大了拦截概率;每个目标的防御效率f1和作战资源损耗f2如表3所示,各算法仿真结果对比如表4所示。

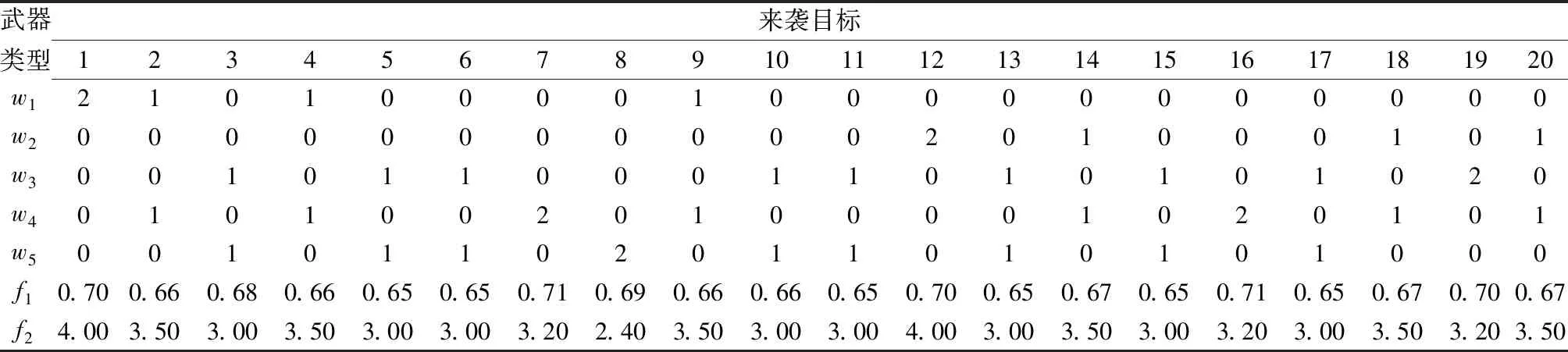
表3 WTA结果

从表4可以看出,在第2组和第4组实验中,NS-MOQGA算法与MOQGA算法的仿真结果接近,在第1组和第3组实验中,NS-MOQGA算法结果优于MOQGA算法,但是总体而言,这两种算法的实验结果都优于NSGAⅡ算法,而在射击稳定方面,NSGAⅡ算法在这4组实验中均有一定的优势。

第1组仿真实验优化目标的收敛速度如图4所示。从图4不难发现,NSGAⅡ算法收敛速度较快,且容易陷入局部最优,NS-MOQGA算法结合MOQGA算法的量子旋转和NSGAⅡ算法非支配排序精英保留策略的思想,收敛结果较好。

在防空反导过程中,作战时机稍纵即逝,留给WTA的考虑时间很短暂。因此,算法收敛速度是衡量算法的重要指标。针对上述4组实验,每组实验采用相同数据重复50次,每次迭代500次,3种算法消耗时间的平均值如图5所示。

图4 目标函数收敛曲线 Fig.4 Convergence curve of objective function

图5 各算法时间消耗对比图 Fig.5 Comparison chart of time consumption of each algorithm

其中,NSGAⅡ算法消耗时间最少,平均为67.211s左右,NS-MOQGA算法消耗时间最长,为81.215s左右。由于NS-MOQGA算法结合了MOQGA算法与NSGAⅡ算法的核心步骤,因此计算时间较长,这种情况是正常的。但实际上,在仿真实验时,由于NS-MOQGA算法收敛速度较快,因此其不需要迭代500次。通过仿真观察，该算法只需迭代100次,基本上就可达到稳定状态,消耗时间为15s左右。因此,总体而言,NS-MOQGA算法无论是在结果或是收敛速度方面,相比其他两种算法均具有一定优势。

4 结束语

针对海上要地防空反导面临的诸多不确定因素,战场态势具有高度不确定性、复杂性和动态性,本文研究了模糊动态环境下的WTA问题,构建了模糊多目标DWTA模型,在MOQGA算法和NSGAII算法的基础上,提出了NS-MOQGA算法。仿真实验结果表明,所提算法具有较好的收敛性能,所构建的DWTA模型和求解算法可为作战指挥员在决策WTA时提供辅助决策和数据支撑。后续还将对多海上要地联合防空反导时的WTA问题进行更加深入的研究。