多局部节点异步航迹快速关联算法

国佳恩, 周 正, 曾 睿

(1. 海军航空大学, 山东 烟台 264001； 2. 中国人民解放军91422部队, 山东 烟台 264001; 3. 中国人民解放军92325部队， 山西 大同 037001)

0 引 言

分布式多传感器融合系统依赖精准的航迹关联结果，以实现目标航迹的融合及多目标跟踪[1-2]。航迹关联是航迹融合的基础,其核心在于寻找可以度量多源航迹的相似性测度,并通过代价函数反映航迹的接近程度,以此实现航迹的同源匹配[3]。

在航迹的相似性度量上,文献[4]对航迹点坐标进行灰关联分析,通过灰关联度刻画不同航迹组合的相似性。文献[5]在灰关联度的基础上进行了进一步改进,应用虚实混合航迹序列解决航迹异步问题。文献[6]基于灰色关联度提出一种两级实时航迹关联算法,可有效应对航迹交叉及施放干扰等情形。拓扑理论同样可应用于航迹间的相似性描述,文献[7]参考拓扑特征描述航迹相似性,对传感器误差具有较强的不敏特性。文献[8]同样基于拓扑关系,通过构建拓扑三角形并采用最大系数原则实现了海上目标的航迹关联,并具有抗差效果。文献[9]提出基于相干点漂移的概率方法，解决了误差条件下的关联-跟踪问题。针对传统方法无法有效度量多源异步航迹时空相似性的问题,文献[10]提出了一种适用于多源异步航迹的相似性度量模型,借助近似时空特征匹配点的思想确定航迹的最优匹配结果。同样基于航迹的时空相似性,文献[11]定义了区间序列与区间点的K近邻区间距离度量,实现了异步航迹的抗差关联。文献[12-13]进一步摆脱前人将距离作为航迹相似性度量的固有范式,从航迹数据离散度的角度切入,分别定义区间离散度及概率区间离散度,以刻画航迹的离散程度,其关联效果优于当前最优算法,为航迹关联问题的解决提供了崭新的思路。

在融合系统中,传感器数目的增加为获取准确的目标位置提供了基础,但如何应对多传感器背景下的高维航迹数据是当前的一个难题[14]。现有算法多是基于两局部节点,应用场景较为单一,将其直接应用到多传感器时关联效果不佳。针对该问题,文献[15]将两局部节点中的二维分配方法扩展为多维分配,并应用灰关联分析求解关联结果,首次实现了多节点条件下的航迹准确关联。文献[16]提出了一种基于最大似然的残差估计配准方法和基于目标密度的序列最佳航迹关联算法,有效解决了由多个传感器测量的目标数量不一致时的关联问题。文献[17]则采用本地联合概率数据关联滤波器,将检测幅度及聚类相结合,完成多传感器航迹关联。

在从双节点到多节点的迁移上,现有算法[18-20]多是采用多维分配的关联判定方法,而其巨大的运算量使得该类算法在关联实时性上存在不足。文献[21]提出的算法具备一定的实时关联优势,但其应用范围较窄,所定义的多普勒频差加权因数仅在双基地高频地波雷达跟踪系统中具备应用价值,可迁移性不强。因此,目前亟需一种可应用于多节点的且能广泛移植的航迹快速关联算法,能以较低的运算量实现密集目标环境下的航迹实时关联。

为解决航迹异步和多局部节点等复杂环境下航迹关联困难且关联效率低下的问题,本文提出了一种基于多维次序匹配的多局部节点异步航迹快速关联算法。首先,以离散度作为航迹相关性度量指标解决航迹的异步关联问题,然后在其基础上进行改进,设计了基于虚实混合序列的时序离散度(temporal discrete degree, TDD)用于刻画航迹状态,并采用本文提出的多维次序匹配算法进行关联判定,从航迹相似性计算及关联判定两个阶段减少运算量,可实现多节点条件下的航迹快速关联。同时，设计了用于辨别航迹交叉等误关联情形的TDD线性趋势系数(TDD-linear trend coefficient, TDD-LTC)检验,有效提升了正确关联率。

本文内容安排如下:第1节介绍了基于虚拟航迹重构的虚实混合航迹序列及TDD概念;第2节对多局部节点的航迹快速关联算法进行了介绍,包括多维次序匹配原理及二次检验步骤的具体实现;第3节则对本文提出的算法从正确关联率及关联速度的角度进行了仿真检验。

1 虚实混合航迹序列的TDD

定义 1虚实混合航迹序列

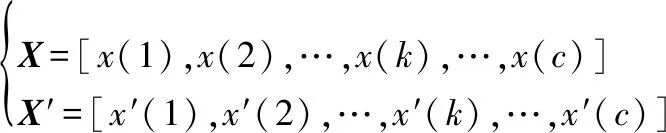
(1)

假设X,X′分别是某一节点采集的某航迹的状态估计及该节点的虚拟航迹,其中k=1,2,…,c代表航迹长度,虚拟航迹的设置满足如下条件:

(1) 每一局部节点对应一个虚拟节点,虚拟航迹由虚拟节点生成,各节点虚拟航迹有且只有一条;

(2) 虚拟节点与对应局部节点的采样频率一致但存在固定采样时延,同一融合周期内虚拟航迹点数与本节点最长航迹点数一致;

(3) 不同局部节点对应的虚拟节点与虚拟航迹均不同;

(4) 虚拟航迹的取值单独定义。

则由某一节点采集的量测航迹及该节点对应的虚拟航迹所构造的虚实混合航迹序列Z定义为

Z=[Z(1),Z(2),…,Z(k),…,Z(c)]

(2)

由于初始采样时延的存在,虚实混合航迹序列为虚拟航迹点与真实航迹点按时序交叉排布的航迹序列,Z(k)为真实航迹点与虚拟航迹点构成的二元虚实混合向量,Z(k)=(x(k),x′(k))。

定义 2TDD

虚实混合航迹序列为一组由二元虚实混合向量依照航迹点上报至融合中心的次序进行排布的序列,其TDD定义为

(3)

式中:

式中:A(k),V(k)是采用递推方式得到的虚实混合航迹序列中前k个元素的均值及方差。初值满足:

与离散度不同的是,当前时刻TDD的计算仅需依靠当前的航迹数据及上一时刻的TDD数据,无需对所有数据进行重复运算,大大提升了运算效率。

此时,虚实混合航迹序列Z对应的TDD序列G为

G=[G(1),G(2),…,G(c)]

(4)

2 多局部节点异步航迹快速关联算法

2.1 基于TDD的航迹状态描述

假设各局部节点的公共观测区域一致,不存在独立观测区域,则对m个异地配置的局部节点H1,H2,…,Hm,其获取的目标航迹数一致。记各节点观测的航迹集合为

(5)

(6)

以位移分量x为例,假设观测区域内共有n个目标,则局部节点i在一个融合周期内获取的航迹状态矩阵为

(7)

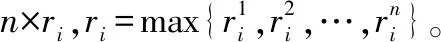
依照定义1给出的虚拟航迹构造原则,对融合系统中的所有节点构造虚拟航迹,得到虚拟航迹组:

(8)

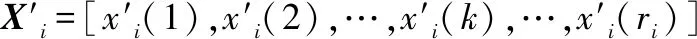
结合虚拟航迹对原航迹状态矩阵进行插值重构,得到局部节点i获取的基于虚实混合航迹序列的状态矩阵:

(9)

式中:

基于虚实混合航迹序列的状态矩阵维度与原状态矩阵维度一致,矩阵元素为虚拟航迹点与真实航迹点构成的二元虚实混合向量,即

(10)

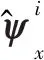
(11)

2.2 基于多维次序匹配的航迹关联判定

在以往的多局部节点航迹关联研究中,无论是利用几何距离或是离散度作为航迹的相似性度量,关联判定阶段都需应用多维分配算法进行同源航迹的匹配运算,虽然该算法可以求得给定条件下的全局最优解,但是约束条件使得其求解过程过于复杂,拉格朗日松弛算法的引入解决了多维分配算法中的组合优化难题,其最优解的逼近过程也十分耗时,在实际应用中关联速度较慢,亟需快速关联算法的提出,以实现航迹的实时关联。

表1随机模拟了具有相同采样周期的3个局部节点采集的小批量航迹数据及虚拟航迹(各节点虚拟航迹相同)。按照定义1的方式构造虚拟航迹并对原航迹进行插值重构,可得到9组虚实混合航迹序列,分别求解各航迹序列的离散度并按离散度大小在节点内进行排序(降序),排序结果如表1所示。

表1 航迹数据及离散度排序结果

由表1可以看出,对应同一目标的同源航迹在分别与虚拟航迹构造虚实混合航迹序列后,其离散度在对应节点内的排序结果相同。这是因为离散度衡量的是数据偏离中心的程度,而同一目标在不同节点上的量测数据相差不大,在与同一虚拟航迹进行混合后,其混合航迹序列离散度差异小于非同源航迹,因此可根据离散度的次序进行航迹关联,将各节点中离散度次序相同的航迹作为对应同一目标的同源航迹。

仿真实验是对混合航迹序列的全局离散度进行的单维次序匹配,下面结合TDD给出基于多维次序匹配的航迹关联判定方法。

首先给出虚拟航迹的构造方法。由于不同节点的采样周期存在差异,依据定义1给出的虚拟航迹构造原则分别构造虚拟航迹。对于不同节点,在各扫描周期内选取坐标最大的位移分量构造虚拟航迹点,并按时序排布构造虚拟航迹,虚拟航迹在位移分量x上的状态向量为

(12)

(13)

当目标数及节点数较多时,对大批量航迹数据进行单维次序匹配的错误关联率较高,难以满足实际任务需要。为获取更为可靠的关联结果,除利用x,y两组位移分量进行双重检验,还可从Gi中抽取多组TDD序列进行多维次序匹配,将航迹起始阶段的离散度信息纳入航迹关联判定,以实现航迹的精准关联。

多维次序匹配的维数即进行次序匹配的次数,维数的确定依赖于航迹长度、航迹数目及节点数。一般而言，航迹越长、航迹数或节点数越多,就需要进行更多的次序匹配,以保证关联效果。在维数确定后,需要抽取不同维度的TDD序列,TDD序列的维度指其在TDD矩阵中的列号。为获得较高的正确关联率,给出多维次序匹配的TDD序列抽取原则:

(1) 确保从各TDD矩阵抽取相同维数及相同TDD序列,进行次序匹配;

(2) 尽可能保证各维度间隔相同;

(3) 匹配维数应大于1,同时尽量避免各抽取维度间隔过近;

(4) 原则优先级为(1)>(2)>(3)。

依照TDD序列的抽取原则可避免由单维次序匹配导致的关联正确率过低,同时避免由匹配次数过多导致的运算量增加。

假定抽取了S组TDD序列进行S维次序匹配,则结合x,y两组位移分量可得到2×S组关联航迹组合:

(14)

对S维次序匹配2S组关联结果,定义关联判定函数:

(15)

由此,基于多维次序匹配的关联判定算法步骤可描述如下:

步骤 1根据航迹长度、航迹数目及节点数目,确定多维次序匹配的维数;

步骤 2根据匹配维数抽取TDD序列,进行排序;

步骤 3依据排序结果进行多维次序匹配,确定关联航迹组合;

步骤 4根据关联判定函数确定最终关联结果。

区别于两局部节点正确关联率的单一性,多局部节点对应同一目标的观测航迹有多种关联结果,需要对多节点情况下的正确关联率进行分级,以更全面地表征算法关联效果。

定义 3多局部节点p元正确关联率

若将每一个目标设定为一个类别,则关联判定即是将所有航迹针对目标类别进行分类的过程。对于m个局部节点,n个目标,经过关联判定后每个目标类别内都有m条航迹,假定以节点1的航迹号作为目标类别号,则对于目标类别j,其类内正确分类数为

(16)

式中:

多局部节点p元正确关联率即各目标类别中类内正确分类数大于等于p的概率,即

(17)

其中，

表示类内p元正确关联数。

2.3 TDD-LTC检验

图1(a)模拟了航迹的合并(分叉、交叉)现象，其中蓝色航迹分别表示节点2中与节点1某航迹对应的同源航迹及合并(分叉、交叉)航迹。在仿真实验中,航迹起始阶段横坐标相同,为纵向合并、分叉及交叉。分别计算3种特殊情况下混合航迹序列TDD的变化趋势,计算结果如图1(b)和图1(c)所示。

图1 航迹合并、分叉、交叉及时序离散度变化情况Fig.1 Track merge, fork, cross and temporal discrete degree change trend

由图1可以看出,无论在位移分量x或y,同源混合航迹序列与合并(分叉、交叉)混合航迹TDD在航迹终点相差不大。这是由于航迹合并(分叉、交叉)时同源航迹与合并(分叉、交叉)航迹的几何中心存在重叠,导致TDD差异不明显。若不进行二次检验,无法有效区分同源与合并(分叉、交叉)航迹,容易造成误关联。

由于航迹起始阶段的横坐标相同,因此同源混合航迹序列与合并(分叉、交叉)混合航迹TDD在x位移分量上相差不大,且均保持了较为平滑的递增趋势,而在y位移分量上则显现出了差异。由此,根据TDD随航迹获取过程的趋势差异,引入TDD-LTC检验来进行航迹合并(分叉、交叉)辨别。

定义 4TDD-LTC

定义虚实混合航迹序列前k个元素的TDD-LTC为

(18)

式中:

同源航迹TDD是缓慢递增的,因此其混合航迹序列TDD-LTC趋近于1;而TDD在航迹合并(分叉、交叉)时具有反向趋势,因此合并(分叉、交叉)混合航迹序列的TDD-LTC较小。实际判别过程可以以0.9为界,若TDD-LTC大于0.9,则表明混合航迹序列TDD递增趋势较强,可视为同源航迹;若TDD-LTC小于等于0.9,表明混合航迹序列TDD趋势存在波动,认为关联到合并(分叉、交叉)航迹,不予关联。图2是本文算法的流程图。

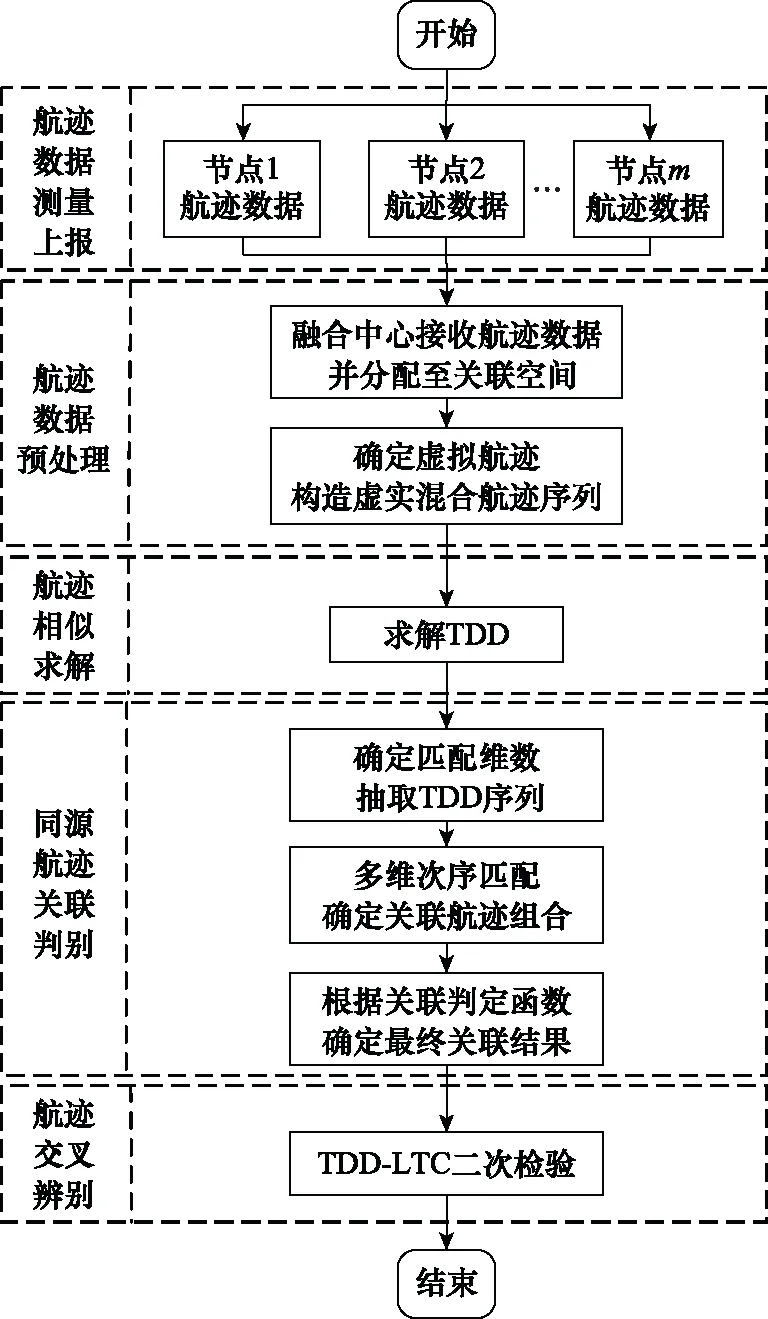
图2 本文算法流程图Fig.2 Flowchart of the proposed algorithm

3 仿真分析与检验

3.1 仿真环境

假设由6个局部节点构成对200 km×200 km目标空域的监视跟踪系统,各节点位置及技术参数如表2所示。仿真实验共模拟60批次目标,各目标初始位置随机,初始航向不定,设定目标做匀速直线运动,速度范围为[200 m/s,600 m/s]。

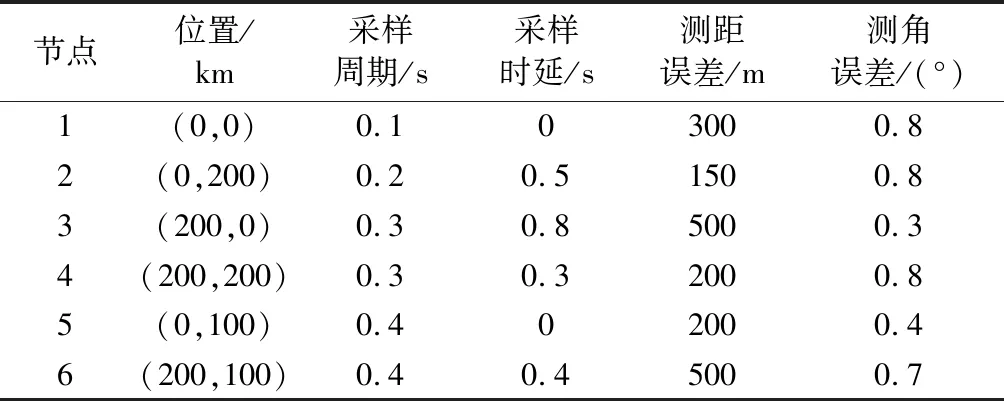
表2 各节点位置及技术参数

采用分级正确关联率对各算法进行性能评价,并采用箱线图形式对其进行表示,如图3所示。

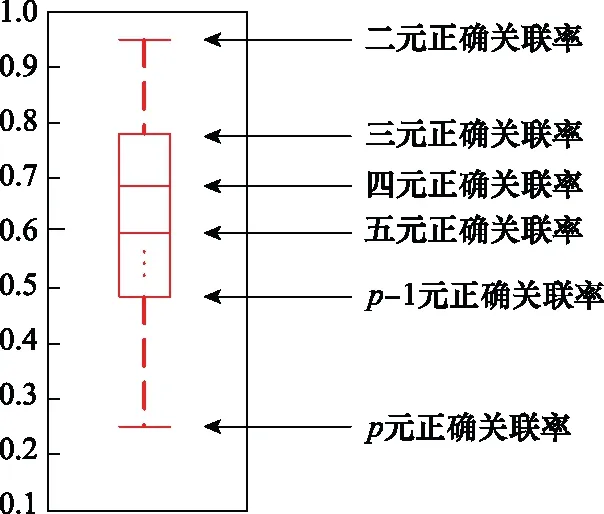
图3 分级正确关联率图形表示Fig.3 Graphical representation of hierarchical correct correlation rate

3.2 算法关联精度分析

图4是本文算法及文献[5]和文献[13]所述异步关联算法随仿真步长的分级正确关联率对比。由于文献[5]和文献[13]所述算法无法直接被应用于多局部节点,因此将其分别与多维分配算法进行组合,来检验其关联精度。

图4 分级正确关联率随时间步长的变化情况Fig.4 Change of hierarchical correct correlation rate with time step

从图4可以看出,本文算法关联精度随仿真时长变化不明显,而文献[13]算法呈现出了较明显的下降趋势。这是由于航迹数据量随仿真时长的增加不断增大,而数据规模越大,不同航迹的离散度可辨别性越差,不同航迹间离散度的相似性导致错误关联率增大。而本文算法采用的多维次序匹配方式克服了传统算法仅进行单次关联判别带来的偶然性,多维TDD序列的匹配将航迹起始阶段的信息也纳入到了关联判定中,因此对不同规模的量测数据具备不敏特性。由文献[5]算法得到的各级正确关联率均低于上述两种算法,关联效果不佳。模拟不同数量的目标,观测算法的关联效果如图5所示。

图5 分级正确关联率随目标数的变化情况Fig.5 Change of hierarchical correct correlation rate with target number

由图5可以看出,多节点情况下随目标数目的增多,三类算法的关联质量均有所下降。本文算法采用的多维次序匹配方法在进行单维匹配时的TDD序列元素个数与目标数一致,因此在进行次序匹配时增大了误匹配率,导致整体正确关联率出现下降,但由于采用了多维次序匹配,匹配次数的增加在一定程度上抵消了误关联概率,使得相同条件下本文算法的关联效果略逊于多维分配算法,但相差不大。

不同节点数各算法的平均正确关联率如表3所示。

表3 平均正确关联率随节点数的变化情况

从表3可以看出,节点数的增多同样增大了关联的难度。在进行多维次序匹配时,TDD次序相同,则其对应的航迹被认为是同源航迹,节点数越多,同源航迹组内的元素个数越多,多节点航迹全部正确关联的难度就越大。对于具有m个节点的融合跟踪系统,其m元正确关联率也就越低。采用多维度的次序匹配同样在一定程度上抵消了由节点数增加带来的误关联,使得相同条件下本文算法与多维分配算法关联效果相差不大。

图6是对不同算法的异步关联效果的检验结果。本文算法是在离散度基础上进行的改进,仅运算方式存在差别,因此适用于异步航迹的直接关联,且关联效果与文献[13]提出的方法基本相同,验证了TDD在进行异步关联时的有效性。

图6 分级正确关联率随采样率的变化情况Fig.6 Change of hierarchical correct correlation rate with sampling rate

3.3 算法快速关联效果分析

由于本文算法采用多种方法提升多节点条件下的航迹关联速度,在航迹相似性计算及关联判定阶段都进行了算法创新,因此采用组合的方式对算法的快速关联效果进行检验。

图7是对目标空域观测时间不同时系统的关联耗时情况。

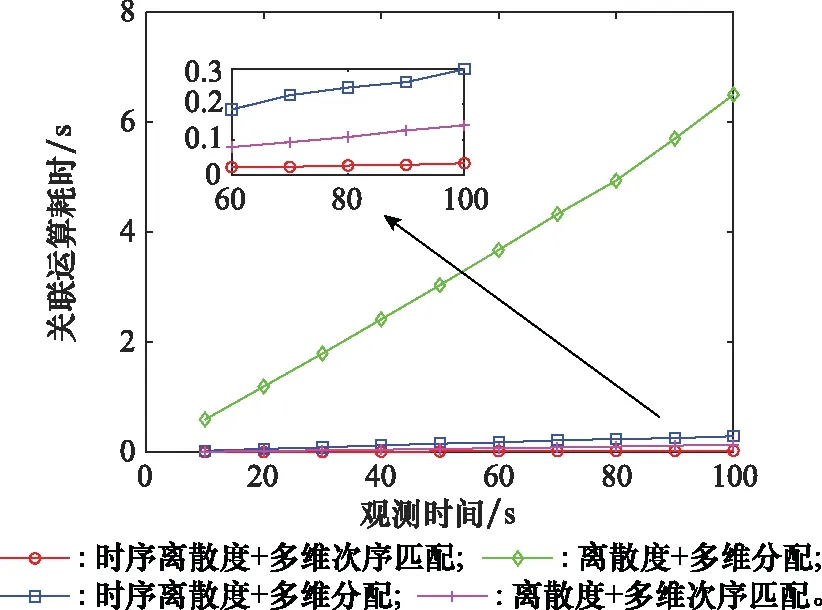
图7 关联运算耗时随观测时间的变化情况Fig.7 Change of correlation operation time with observation time

一般而言,观测时间越长,航迹数据规模越大,关联解算所需的时间也就越长。可以看出,本文算法在关联速度上最具优势,将TDD及多维次序匹配算法分别与传统算法进行组合后,系统关联运算耗时亦有所下降。而文献[5]方法需要对原始航迹数据进行虚实混合序列变换,该步骤及后续灰关联度的求解均十分耗时,导致算法运算效率较低。

同样,以m个节点及n个目标为例,假设航迹点数为r,不同组合算法的运算量比较如表4所示,其中①、②、③、④分别代表TDD、离散度、多维次序匹配、多维分配。

多维次序匹配的实现依赖于多维度的TDD序列,若采用文献[13]的离散度计算方式,则会不可避免地导致数据的重复运算;而本文设计的TDD仅依赖上一时刻运算得到的离散度与当前上报的航迹数据,即可递推得到当前的离散度,将文献[13]中离散度的整体运算分散到航迹上报的各个时刻,在获取不同维度离散度数据的同时降低了运算量,有效提升了关联速度。

表4 不同组合算法的运算量比较

多维次序匹配则克服了传统多维分配算法的速度缺陷,巧妙地利用离散度在衡量数据离散程度上的固有特性,用次序匹配替代全局运算,经一次排序便可完成对所有航迹的关联解算,使算法复杂度大大降低。图8是不同目标数目下的系统运算耗时。由图8可以看出,本文算法在不同目标数下均取得了最佳关联速度,较低的运算耗时也使得融合中心可以一边接收各节点上报的航迹,一边进行实时的关联解算。

图8 关联运算耗时随目标数目的变化情况Fig.8 Change of correlation operation time with the number of targets

继续改变局部节点数目,检验本文算法的快速关联效果,结果如表5所示。

表5 关联运算耗时随节点数变化情况

结合表5及图4～图8可以看出,本文提出的TDD及多维次序匹配算法均能有效提升关联速度,相比传统算法优势明显,在不损失关联精度的同时实现了航迹的快速关联。

3.4 对航迹合并、分叉及交叉的辨别

现代战场空情复杂多变,战场形势的要求及飞行器机动性能的提升使得航迹的合并、分叉及交叉等现象愈发普遍。图9是不同的航迹合并、分叉及交叉比例下各算法的关联效果。

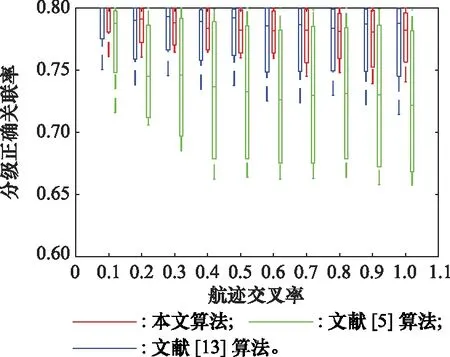
图9 分级正确关联率随航迹交叉比的变化情况Fig.9 Change of hierarchical correct correlation rate with track crossing ratio

由于增加了TDD-LTC二次检验环节,本文算法在不同的空情复杂度下均实现了较高的正确关联率,对于航迹合并、分叉及交叉的辨别要优于文献[5]和文献[13]。文献[5]采用虚实混合序列的方式进行关联,并没有针对航迹交叉等情形提出解决方法,因此当航迹交叉率较高时,其关联效果较差。文献[13]针对航迹交叉前、后离散度的变化对航迹序列进行分段,并提出采用分段航迹序列离散度对由航迹交叉导致的关联困难问题进行解决。但是,从关联效果来看,文献[13]所提算法不及本文算法,这是由于分段数目的不同对正确关联率有很大影响,针对不同场景需要采用恰当的分段数,才能取得较好的关联效果。

4 结束语

为实现多局部节点条件下的航迹快速关联,本文采用TDD及多维次序匹配的组合方法降低运算量,采用递推方式克服了传统离散度运算方法的冗余性,而多维次序匹配则避免了由传统多维分配方法的全局运算带来的运算量爆炸,同时多维度的TDD序列综合利用了航迹的整体信息,在不损失关联精度的同时实现了航迹的快速关联,具有良好的应用前景。下一步,将结合实测数据进行算法检验,不断完善算法,使其具备适应不同战场环境的鲁棒性。