基于分布式支持向量机的电网错误数据注入检测法

徐 超，孙金莉，杨 郡，刘颖彤，李韬睿

(1.国网湖北超高压公司，湖北 武汉 430050； 2.国网湖北电力科学研究院，湖北 武汉 430050)

电力系统中拓扑误差，由材料问题导致的通信线路缺陷、仪器故障、恶意攻击等造成的测量数据不良将会影响电网状态估计的准确性[1-2]。例如，许多通信线路供应商为获取巨额利润，有意忽视对通信线的质量保障，采用劣质材料制造通信线；当此类由劣质材料制造的通信线被用作电力系统的通信线路时，可能成为电力系统的安全薄弱点，成为错误数据注入的主要攻击点。不准确的状态估计会误导电网控制决策和引入电力系统控制平台的数据流软错误[3-4]，造成灾难性后果。因此，为了检测电网中的错误数据注入，基于测量残差统计检验的技术得到了广泛的应用[5]。

为保证错误数据注入检测的准确性，提出了大量的错误数据注入检测方法[6-8]。现有错误数据注入检测方法多以残差最小作为检测目标，而错误数据注入是一种具有隐蔽性的恶意攻击，可以绕过传统的基于残差的统计检验方法。为解决该问题并进一步对具有非线性分布特性的电力网络错误数据注入检测的准确性和更好地平衡计算复杂度与检测准确性之间的关系，提出基于分布式支持向量机的电力网络错误数据注入检测新方法。

1 状态估计指标

将电力网络建模为一组非线性方程，表达式[9]:

Z=h(X)+e

(1)

式中：Z∈Rm为测量向量；X∈RN为状态变量向量；h为系统状态变量X∈RN与Z之间关系的函数，h可实现X∈RN→Z∈Rm；e∈Rm为测量平均值为0的测量误差向量，其标准差为σ，且服从高斯概率分布；N=2n-1为待估计的未知状态变量个数(2n为电力系统的总线数)。

(2)

ΔZ=HΔX+e

(3)

式中：H=∂h/∂x是h在X*处的雅可比矩阵；ΔZ=Z-h(X*)=Z-Z*为对测量向量的修正向量；ΔX=X-X*为对状态向量的修正向量。

如果式(3)表示的系统是可观测的，则测量值的向量空间Rm可分解为2个向量子空间的直接和，即：

Rm=R(H)⊕[R(H)]⊥

(4)

式中：由R(H)给出的H的范围空间是一个满足R(H)⊂Rm的N维向量子空；[R(H)]⊥为R(H)的正交补集，即如果u∈R(H)且v∈R(H)，则〈u,v〉=uTR-1v=0。

(5)

求解该方程，可以得到：

(6)

P=H(HTR-1H)-1HTR-1

(7)

因此，在几何上，基于最小二乘法的经典状态估计器可以解释为一个投影矩阵P作用于测量向量ΔZ的校正，校正通过残差实现。另一种可视化状态估计的方法是观察测量误差的几何位置与雅可比矩阵范围空间R(H)的关系。然后，将测量值的向量空间分解为R(H)和[R(H)]⊥的直接和，就有可能将测量误差向量e分解为2个分量——不可检测(eU∈[R(H)]⊥)成分和可检测(eD∈R(H))成分：

e=eD+eU,eD=(I-P)e,eU=Pe

(8)

故，

(9)

式中：前2个分量的区别在于它们属于不同的空间，第1个分量属于R(H)，另一个分量属于[R(H)]⊥，具有不同的性质。

由于残差eD和另一个误差分量eU相互正交，可以组成第i次测量的测量误差向量：

(10)

这个误差矢量称为组合测量误差(CME)。为了找到测量的总误差，使用文献[10]所提出的创新指数Π：

(11)

创新指数Π反映的测量误差的很大一部分没有反映在基于最小二乘法的经典状态估计器的估计残差中，能够更好的识别错误数据注入。已知向量空间R(H)和[R(H)]⊥是正交的，那么就有可能估计第i次测量的组合误差。因此，式(10)将变成：

(12)

(13)

式中：ri为第i次测量的残差；Πi为第i次测量的创新指数。一旦选择了初始状态，这2个量都是已知的。如果使用归一化残差，则得到组合归一化误差(CNE)：

(14)

(15)

式中：σi是第i次测量的标准差。

2 基于分布式支持向量机的电力网络错误数据注入检测方法

所提方法通过蒙特卡罗模拟生成测量计划，该测量计划模拟多种类型的错误数据注入的粗差[11]；基于创新指标概念的2个指标Π和CME将作为所提出检测技术的输入参数。为提高计算效率和避免不必要的资料浪费，使用主成分分析方法简化数据库。

2.1 数据模型

测量计划包括两组测量：标准测量组(变电站现场测量)(SMS)和概率测量组(PMS)(蒙特卡罗模拟定义的测量)[12]。每个案例考虑400个蒙特卡罗样本，它们被用来随机确定一个测量计划。

每个测量平均值的±3 dB内的相关噪声不被视为错误数据注入。为了建立数据库，生成了3 000个具有以下特征的蒙特卡罗样本：

(1)1 000个样本考虑多个测量误差 (数据输入1)。考虑的粗差的测量集在3～20个测量值之间，集合及其大小随机选择，没有临界测量或临界组的存在；

(2)1 000个样本考虑参数误差(数据输入2)，传输线的串联阻抗在4～14 Ω变化。粗差直接添加到行串行参数的大小中；

(3)考虑拓扑排除误差 (数据输入3)的1 000个样本，例如，排除一条线路；其中，被排除的输电线路是随机选择的。

2.2 输入参数

为通过Π和CME作为输入参数识别发生的错误数据输入，考虑Π和CME的平均值、最大和最小标准差；Π和CME的数据是通过具有2个测量平均值的蒙特卡洛模拟获得。

所考虑的一个包含122个测量值的第1组完整测量计划，测量结果如表1所示。其中，14个有功功率注入，14个无功功率注入，40个有功电流注入，40个无功电流注入和14个电压值注入。

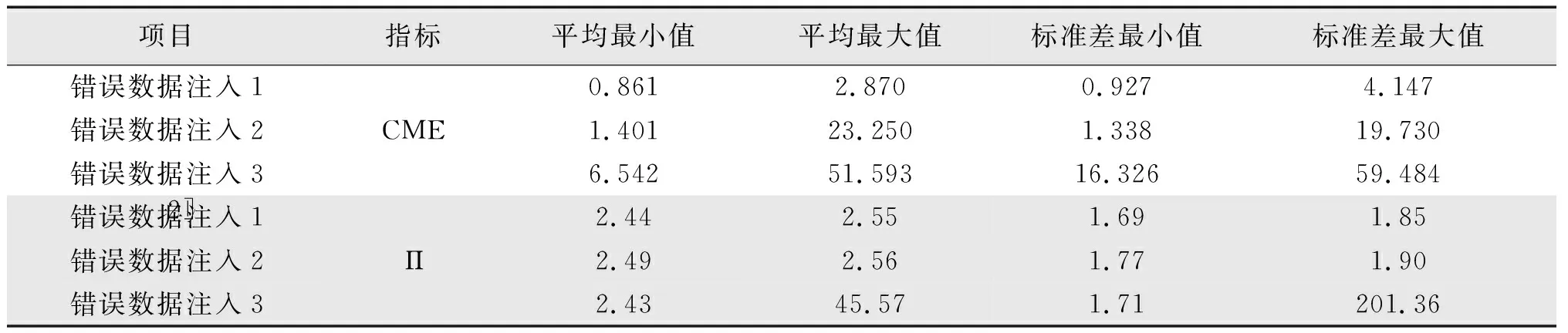
表1 所考虑的一个包含122个测量值的第1组完整测量计划Tab.1 Analysis results of Group 1 measurement plan with 122 measurements

所考虑的一个包含81个测量值的第2组完整测量计划，测量结果如表2所示。SMS为有功功率和无功功率的注入，以及节点1的电压大小改变；PMS为由蒙特卡罗模拟定义的78个测量值，考虑有功和无功功率注入和功率流的正态分布函数。

表2 所考虑的一个包含81个测量值的第2组完整测量计划Tab.2 Analysis results of group 2 measurement plan with 81 measurements

由表1、表2可知，其结果表明，Π和CME有潜力作为变量来检测哪个数据输入导致了粗差。因为最大值和最小值的平均值和标准差在2个测量平面上显示出一定的模式。

2.3 主成分分析

为进行主成分分析，可在方阵的情况下使用特征向量分解(EDC)[13]，在矩形矩阵的情况下使用奇异值分解(SVDC)[14]。

通过SVDC对复数值数据矩阵进行分解时，主成分分析中常用概念：

(1)组织数据集：定义一个维度为n×p的X矩阵，每列代表变量p的单个分组观测；

(2)计算与平均值(B)的偏差：中心X减去列的平均值；

(3)求B的奇异值分解：[U,S,V]=SVDC(B)产生一个对角线矩阵S，其维数与B相同，具有按降序排列的非负对角线元素；通过单位矩阵U和V，使B=USVT；

(4)将COEFF=V定义为主分量的系数，将SCORE =US定义为主要分量分数，即X在主分量空间中的表示。SCORE行对应于观测，列对应于主成分；

(5)通过Xnew=SCORE(:,1:z)×COEFF(:,1:z)T+mean(X)获得近似重构的向量。

2.4 识别方法：分布式支持向量机

分布式支持向量机是一套监督机器学习方法，可用于数据模式分析和数据分类[15-16]。所使用的布式多分类支持向量机方法：

(1)一对一编码设计，定义k(k-1)/2个支持向量机，其中k是唯一类标签的数量；

(2)纠错输出码模型，可减少3类或以上二进制分类器的分类问题。为此，定义一个编码矩阵M∈{-1,0,1}，其中零值表示类尚未对特定分类器的训练进行分类，这就产生了不同的决策边界，从而提高了多类问题分类的准确性；

(3)二进制丢失函数的解码方案。使用Hinge损失函数，它确定了二进制分类器的预测是如何聚合的[17]，也就是说，将新的观测结果分配给类C(控制裕度和训练误差之间转换的参数)，从而最大程度地减少所有k(k-1)/2支持向量机二进制的丢失聚合。

3 仿真研究与分析

采用IEEE 57节点系统进行所提错误数据注入检测方法的仿真实验，并将所提方法对错误数据注入检测效果与中基于矩阵分解算法的错误数据注入检测方法(MST-FDJD)[18-20]进行了对比。

随机误差被添加到所有测量中。生成 3 000 个样本用作训练集(每种错误数据注入由1 000 个样本组成)。生成150 000个样本以测试训练网络 (每种错误数据注入由50 000个样本组成)。

采用创新指标时，对IEEE 57节点系统错误数据注入的检测准确率如表3所示。对IEEE 57节点网络训练，考虑具有339次测量的测量计划(SMS为节点1、2、3的有功和无功能量注入及电压幅度；PMS为由蒙特卡罗模拟定义的330次测量值，考虑有功、无功功率注入和能量流的正态分布函数以及功率流量和电压幅度)。

由表3可知，不考虑网络拓扑变化时所提方法对IEEE 57节点系统的错误数据检测的最大偏差为2.13%，MST-FDJD对IEEE-57节点系统的错误数据注入检测的最大偏差为3.0%；所提方法对所有错误数据注入的检测准确率均高于MST-FDJD对该EG错误数据注入的检测准确率。

表3 不考虑网络拓扑变化时对IEEE 57节点系统的错误数据注入的检测准确率Tab.3 Detection accuracy of false data injection for IEEE 57-bus system without considering network topology changes

为验证电力网络拓扑变化时所提方法对电力网络错误数据注入的识别准确率，考虑了线路拓扑的小重构(在节点之间转移分支或通过隔离器隔离分支)。采用创新指标时，考虑网络拓扑变化时所提方法和MST-FDJD对IEEE 57节点系统的错误数据注入的检测准确率结果，具体如表4所示。

由表4可知，考虑网络拓扑变化时所提方法对IEEE 57节点系统的错误数据注入检测的最大偏差为6.65%，MST-FDJD对IEEE-57节点系统的错误数据注入的最大偏差为37.30%；所提方法对所有EG错误数据注入的检测准确率均高于MST-FDJD对该EG错误数据注入的检测准确率。

表4 考虑网络拓扑变化时对IEEE 57节点系统的错误数据注入的检测准确率Tab.4 Detection accuracy of false data injection for IEEE 57-bus system considering network topology changes

采用创新指标或归一化残差指标时，对IEEE 57节点系统的错误数据注入的检测准确率结果，具体如表5所示。

表5 对IEEE 57节点系统的错误数据 注入的综合检测准确率Tab.5 Table Comprehensive detection accuracy of false data injection for IEEE 57-bus system

由表5可知，所提方法对IEEE 57节点系统的错误数据注入的检测准确率均超过99%，对IEEE 57节点系统的错误数据注入的检测准确率均高于MST-FDJD，且使用创新指标时所提方法与MST-FDJD的对比效果更明显。

以上对比结果表明，所提方法能够准确检测电力网络的错误数据注入，且具有较好的泛化能力和较好的非线性数据分类能力。

4 结语

提出基于分布式支持向量机的电力网络错误数据注入检测新方法。为验证所提错误数据注入检测方法的有效性，在IEEE 57节点系统上进行了错误数据注入检测测试，并将检测效果与基于矩阵分解算法的错误数据注入检测方法进行了对比。结果表明，与已有方法相比，所提方法能够更加准确地检测电力网络的错误数据注入，且具有较好的泛化能力和非线性数据分类能力。