基于优化的灰色关联分析-极限学习机食用油污染物风险评价模型研究

于家斌，范依云，王小艺,3, *，赵峙尧，金学波，白玉廷，王 立，陈慧敏

（1.北京工商大学人工智能学院，北京 100048；2.北京工商大学 中国轻工业工业互联网与大数据重点实验室，北京 100048；3.北京服装学院文理学院，北京 100029）

粮油食品安全问题不仅影响着公众健康，还关系到社会稳定和经济发展等问题。近些年来，粮油食品安全事件屡见不鲜，如“镉大米”[1]、“地沟油”[2]等，这些事件严重危害了公众健康，影响了社会稳定。我国在2015年新修订实施了《中华人民共和国食品安全法》，其中第二章食品安全风险监测与评价的第十七条规定了国家应构建食品安全风险评价体系[3]。而食用油是粮油食品的重要组成部分，是人们日常饮食的重要一环。因此，对食用油中各类污染物进行风险评价具有重要意义。

目前，国内外风险评价方法主要分为定性评价、定量评价以及定性-定量结合评价3 种。定性评价是依据专家经验、调查问卷等方式对风险进行分析判断得出结果，代表性的方法包括德尔菲法、决策树、危害分析临界控制点法[4-6]等，主要应用于食品监管、参与者对食品风险态度以及参与者食品安全意识分析等，定性评价过于依赖评估者的主观判断，无法基于大量高维的检测数据进行风险评价。定量评价方法主要包括两类，一类是通过检测方法获取风险因子数据直接描述风险水平，如气相色谱法、光学传感器法等[7]。另一类是通过数据驱动算法挖掘大量检测数据中的风险规律，从而得到风险程度量化值，如熵权系数法、蒙特卡洛仿真法、支持向量机法、人工神经网络、深度学习等[8-11]，但这类定量评价过于依赖数据，数据中存在噪声会影响评价结果。定性-定量结合方法中具有代表性的方法有层次分析法，其主要是通过建立层次结构模型并结合专家意见构建风险判断矩阵[12]，此外还有如云模型[13]、模糊综合评价法[14]等方法依据隶属度理论将定量风险值以及区间转化为定性语言集，定性-定量结合评价法常用于属性约简[15]、风险分级[16]。综上，现有风险评价方法在实际应用时仍存在一定局限性，如食用油检测数据具有高维性、非线性、离散性的特征，导致传统数据驱动方法评价效率和精度不高；其次，对于数据中的噪声，现有方法并没有针对性的处理，一般只是对数据进行简单地清洗；另外，在利用数据驱动算法建模时，需设置多个参数，例如高亚男等[17]在采用LightGBM模型预测风险值时，需调整叶子节点个数、最大深度和学习率等参数，现有方法一般是利用人工试凑法来进行参数调优，这样凭借经验进行参数的试错，是主观且繁琐的。

鉴于现有风险评价方法存在的问题，国内外专家学者进行了大量研究。针对数据中的噪声问题，有学者利用基于小波理论的小波阈值法进行了滤波处理研究，例如Chen Jian等[18]利用小波软阈值法对电力系统中低频振荡信号产生的噪声进行滤波处理并取得良好效果。在针对食用油检测数据这类以高维性、非线性、离散性为基础的数据进行评价模型构建时，灰色关联分析（grey relational analysis，GRA）能够从大量复杂和非线性数据中分析不同指标之间的灰色关联系数从而制定指标的权重，如Han Yongming等[19]通过对乳制品9 类指标的GRA确定了指标权重。极限学习机（extreme learning machine，ELM）作为一种单隐层前馈神经网络，其随机产生输入层权值和隐层偏置的特性[20]，使其对数据中的噪声有一定抑制能力，并且相比于传统基于梯度下降的数据驱动评价算法具有更好的泛化能力和更快的速度，例如Zaher等[21]采用ELM预测泡沫混凝土的抗压强度，效果优于支持向量机回归等传统数据驱动模型。针对模型参数设置主观性强的问题，贝叶斯优化算法常用于超参数调整，是解决模型拟合问题的理想选择，例如Acerbi等[22]提出一种混合贝叶斯优化算法并进行了模型拟合实验，结果表明该算法要优于其他常见的优化算法。

综上，针对食用油检测数据的特点以及传统风险评价方法中存在的问题，本实验首先在风险评价模型前端加入基于小波阈值法的数据滤波模块；接着结合GRA和ELM的优势，对滤波后数据进行GRA得到每种风险指标权重并融合为多指标综合风险值作为风险值标签，利用ELM网络训练并输出综合风险值；在上述过程中利用实用贝叶斯优化（practical Bayesian optimization，PBO）算法分别优化滤波模块和ELM网络参数；最后对综合风险值进行模糊综合分析得到风险等级划分结果。

1 材料与方法

1.1 数据特点以及预处理

本实验收集整理了国内某食用油主要产出省2017—2019年共11 345 行、150 组花生油检测数据，数据主要呈现以下特点[23]：1）高维性：每个食用油样品的抽检信息由不同属性组成，如抽样编号、产地信息、产品信息、生产日期、检验项目、检验结果、关键限值等。这些属性相互独立，并且很多属性如抽样编号等对于风险程度的判断是冗余的，需要滤除掉。2）离散性：一个食用油样品大约有几十种检测指标，一个指标维度与另一个指标维度不同，而各项指标的国家标准也不同。这意味着这些指标具有不同的离散域，检测结果在离散域中也是无序的。因此，需要从这些指标中筛选出影响风险程度的关键指标。3）非线性：每个检查信息包括数值信息和描述信息。数值信息包含大量空值，描述信息也包含了一些离散值。在完整的检验信息中，不同属性之间的信息分布是不对称和不平衡的，增加了风险分析难度。因此，需要进行指标筛选以及数据预处理工作。

首先进行指标筛选，食用油检测指标种类繁多，包括酸值超标检测、过氧化值检测、溶剂残留量检测、金属污染检测、化学污染检测和生物毒素检测等。但并不是上述所有的检测项都能作为食用油的风险评价指标，需要从其中筛选出对食用油风险程度影响较大的指标。本实验分析各项指标的检出情况，参考文献[24]，选取酸值、过氧化值、砷含量、铅含量、黄曲霉毒素B1含量和苯并[a]芘含量这6 项指标作为关键的风险评价指标。食用油的酸值和过氧化值是食用油的基础类风险指标，砷、铅是食用油中常见的重金属类污染物，黄曲霉毒素B1则是食用油中常见的真菌毒素类污染物，苯并[a]芘是食用油中主要的化学类污染物，这6 项指标能够代表相应类别的污染物，同时相对于其他风险指标更容易被检出，因此通过这6 项指标能够基本判断食用油的风险程度。

其次进行数据预处理，步骤如下：1）删除无用信息。每个样本都有许多描述性字符，有必要简化这些信息以强调影响风险程度的特性，剔除与食品安全关系不大的食品感官类指标，如口感、颜色、形状等。2）删除多余符号。例如某个食用油样品总砷的检测结果为“＜0.01 mg/kg”，总砷的限值不高于0.25 mg/kg，该样品总砷的检测结果并未超过限值，则去掉结果中的“＜”符号，将检验值记录为“0.01 mg/kg”。3）使用极小值替代未检出指标数据。本实验对未检出指标数据的处理参考文献[15]，具体方法为针对检测结果为未检出的指标数据，利用极小的数字“0.001”代替“未检出”，而不是用“0”代替。这是为了保证得到的输入矩阵能够被评价模型识别并且是正定的。至此指标的筛选以及数据预处理工作完成。

由于篇幅限值，仅列举了部分原始检测数据，如表1所示，对其进行预处理之后的数据如表2所示。

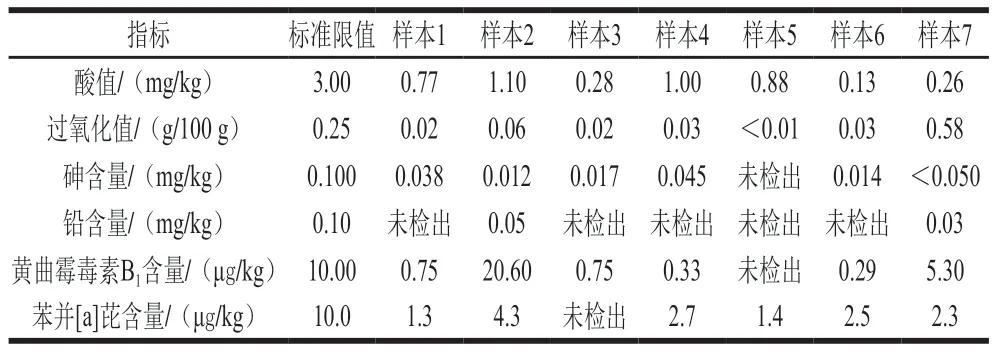
表1 食用油部分原始检测数据Table 1 Selected raw chemical data of edible oil samples

表2 预处理后的食用油数据Table 2 Preprocessed chemical data of edible oil samples

1.2 风险评价模型

如图1所示，本实验提出的风险评价模型主要分为基于小波阈值法的数据滤波模块和基于GRA-ELM的评价模块，PBO算法则负责优化滤波模块和ELM网络中的重要参数，ELM网络输出的综合风险值通过模糊综合分析得到食用油样品所属风险等级。

图1 风险评价模型整体算法流程图Fig.1 Overall algorithm flow chart of risk assessment models

1.2.1 基于小波阈值的滤波模块

食用油检测数据可能会含有噪声，这些噪声会影响最终评价结果。Huber[25]对模型鲁棒性进行了3 个层面的解释：1）模型具有较高的精度或有效性；2）对于模型假设出现的较小偏差（如噪声），只能对模型产生较小的影响；3）对于模型假设出现的较大偏差（如突变点），不会对模型性能产生较大的影响。实际进行风险因子含量检测时，传感器可能会产生散粒噪声、热噪声、低频噪声等，其中散粒噪声和热噪声影响较大，这两种噪声都是白噪声。因此，为了充分验证模型的鲁棒性并尽可能模拟实际情况会产生的噪声干扰，本研究对原始食用油检测数据的噪声方差进行了修改，如式（1）所示。

将上述得到的数据输入到滤波模块进行滤波处理，滤波模块主体是小波阈值法，小波阈值法主要原理为设置一个临界阈值，经小波变换后，所得小于阈值的小波系数主要是由噪声引起，这部分系数需要被滤除掉，反之大于阈值的系数则是由信号引起，该部分系数需要被保留，最后通过小波重构得到滤波处理后的信号。本研究小波阈值法去噪分为3 个步骤：1）使用离散化小波变换将信号转变到小波域；2）对各尺度上的小波系数做阈值量化处理；3）小波重构得到滤波后信号。

具体地，小波阈值去噪过程首先需进行离散小波变换（discrete wavelet transform，DWT）过程，DWT实际上是一个分解过程，分解则需选取小波分解层数和母小波函数类型，这个过程由贝叶斯优化算法自适应选取。在分解完成后会得到对应层数的高频和低频分量，这时需要选择合适的阈值σ进行噪声的平滑处理，经小波变换转到小波域之后，白噪声仍然呈现出较强的随机性，因此小波域中更容易区分噪声与信号，小波变换后各个分量中原始数据的有效信号对应较大的系数，而此时原始数据中的噪声对应较小的系数。假设在小波域中噪声的方差为σ，依据高斯分布特性，99.9%的噪声系数都在[－υ，υ]范围内，接着设定合适的阈值，通过比较信号绝对值和阈值的大小，将小于阈值的点重置为零，大于或等于阈值的点重置为该点信号与阈值的差，即实现了噪声的平滑处理，上述过程如式（2）所示。

式中：Di,t表示第i层分解结果的高频子序列索引为t的数据；λi是间接调节阈值的比例系数，其取值范围为λi∈（0,1），i＝1,...,N；σ为噪声估计方差；median表示被平滑序列的中位数；Di为分解后索引为i的高频子序列；0.674 5为高斯噪声标准方差调整系数；T为被去噪序列长度；γ为根据估计的噪声方差所计算的每个子序列噪声的估计阈值；而最终的阈值υ是通过比例系数λ的值调整估计阈值γ得到的；由于各个子序列中的噪声含量不同，因此在平滑处理每个分量时对应的λ均不同，而每个λ则是通过PBO算法自适应选取的，这样可以对不同数据中的噪声进行平滑处理。具体PBO算法会在1.2.3节详细介绍。优化最后对每层高频分量滤波处理后，通过小波重构得到估计真值，如式（3）所示。

1.2.2 基于GRA-ELM的风险评价模块

1.2.2.1 灰色关联分析

GRA是一种多因素分析方法，它通过比较统计集合之间的几何关系来划分复杂系统中多因素之间的关系[26]。GRA主要包括以下步骤：1）利用GRA对指标进行赋权；2）计算综合风险值。

首先需要获取参考向量和比较向量，设参考向量为x1＝{x1(1),x1(2),...,x1(n)}，n为食用油样本个数。比较向量为xj＝{xj(1),xj(2),...,xj(n)}，j＝1,2,...,m，m为风险指标个数。对m组指标进行归一化处理，消除量纲的影响，如公式（4）所示。

然后计算关联系数，k时刻的fj（k）和f1（k）的灰色关联系数如公式（5）所示。

式中：ξj（k）为灰色关联系数；ρ为调节参数，可以使各个系数的差异性增强，ρ∈（0，1）。序列f1和序列fj间的关联系数见公式（6）。

为了保证结果的准确性，用每个风险指标各充当一次参考序列，则可得到所有风险指标的相关系数矩阵，见公式（7）。

本研究指标间关联系数矩阵计算结果如表3所示，例如酸值对于自身灰色关联系数为1，与过氧化值、砷含量、铅含量、黄曲霉毒素B1含量和苯并[a]芘含量的灰色关联系数分别为0.688 1、0.820 6、0.770 0、0.966 1和0.722 3。

表3 风险指标灰色关联系数矩阵Table 3 Gray correlation coefficient matrix of risk indicators

根据表2可得权重向量，如公式（8）所示。

式中：m为风险指标个数；γij为表3中第i行指标与第j列指标之间的灰色关联系数。

则权重向量W＝[0.173 980 203，0.150 610 512，0.172 256 898，0.168 421 495，0.174 607 178，0.160 123 714]。

接下来需要计算综合风险评价值，首先需要进行无量纲化处理，具体为用风险因子的实际检测值与指标关键限值α的比值表示相对风险值，如公式（9）所示。

式中：Pij为第j类风险因子的第i条检测含量结果xij经无量纲化处理后得到的相对风险值，其中i＝1,2,...,n，j＝1,2,...,m；aj为第j类风险因子的指标关键限值。将公式（8）所得权重向量W与公式（9）中得到的各指标相对风险矩阵相乘，即得到公式（10）。

式中：Y＝[y1,y2,...,ym]T为综合风险评价序列；P为相对风险矩阵；W＝[w1,w2,...,wm]T为权重向量。至此模型的期望输出标签计算完成。

1.2.2.2 极限学习机网络

由Huang Guangbin等[27]提出的ELM是一种新型神经网络学习算法，ELM的网络结构与单隐层前馈神经网络一样，分为输入层、隐含层和输出层，但ELM的训练阶段不再是传统神经网络中基于梯度的算法（后向传播），而是随机生成输入层权值和隐藏层偏置，输出层权重则是通过最小化由训练误差项和输出层权重范数的正则项构成的损失函数，并依据Moore-Penrose的广义逆矩阵理论计算求出，得到所有节点的权值和偏差后即完成了ELM的训练过程，测试数据利用求得的输出层权重即可计算出网络的预测输出。

由于随机生成输入层权值和隐藏层偏置，ELM网络不需要像传统神经网络那样通过一次次迭代得到最终的解，因此ELM网络的计算复杂度低，可调参数非常少，一般为隐层节点数，并且ELM网络在保证精度的同时，学习速度更快、泛化能力更强。图2为ELM的结构。

图2 ELM网络结构图Fig.2 Network structure diagram of ELM

假设有N个任意样本（xi,ti），其中Xi＝[xi1,xi2,...,xin]T∈Rn，ti＝[ti1,ti2,...,tin]T∈Rm，对于一个有L个隐层节点的单隐层神经网络可以按公式（11）表示。

式中：g(x)为激活函数；Wi＝[wi1,wi,2,...,wi,n]T为输入权重；βi为输出权重；bi是第i个隐层节点偏置；Wi×Xj表示Wi和Xj的内积。

ELM学习的目标是使得输出的误差损失最小，可按式（12）表示。

式中：oj表示网络输出；tj表示目标输出。

矩阵表示为式（13）。

式中：H是隐层节点的输出；β是输出权重；T是目标输出。

这等价于最小化式（15）所示的损失函数。

在ELM中，输入权重Wi和隐层偏置bi随机生成后，隐层的输出矩阵H就被唯一确定，ELM的训练过程可以转化为求解Hβ＝T，输出权重β可以被确定，如式（16）所示。

式中：H†是矩阵H的Moore-Penrose广义逆。在本研究中，原始的食用油安全检测数据作为ELM的输入，由公式（8）～（10）所得到的综合风险评价数据作为期望输出，对ELM进行训练，对ELM隐层节点数的参数优化是由PBO算法完成的。

1.2.3 实用贝叶斯优化算法

由1.2.1节可知，小波阈值法中母小波函数、小波分解层数和每层小波高频分量阈值是滤波模块中的重要参数，由1.2.2.2节可知，ELM的隐层节点数目也是重要的参数[28]，这些参数会对模型最终的预测性能产生极大的影响，由于人工选取效率低且存在主观性过强的问题，本研究利用PBO算法，对建模过程中的参数进行优化，该方法将网格自适应直接搜索（mesh adaptive direct search，MADS）与通过局部高斯过程（Gaussian process，GP）执行的BO搜索相结合，主要分为搜索和轮询两个阶段。简而言之，PBO是在一系列快速的、局部的BO步骤（MADS的搜索阶段）和系统的网格探索（轮询阶段）之间交替进行，当搜索阶段失败时，意味着GP模型没有成功优化参数，这时会切换到轮询阶段，轮询阶段执行的是无模型优化，在这个阶段会收集优化目标的信息，以便下次在搜索阶段构建更好的GP模型，直到达到优化目标。

在使用贝叶斯优化时，首先需定义目标函数，但由于ELM的训练过程实际上是一个黑盒过程，因此本实验中使用网络的均方根误差（root mean square error，RMSE）作为PBO算法的目标函数，具体如式（17）所示。

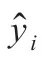
PBO算法伪代码如表4所示。

表4 PBO算法伪代码Table 4 PBO algorithm pseudocode

1.2.4 模糊综合分析

由1.2.2节中评价模型所得的综合风险评价值是对风险的定量评价，但为了给相关监管部门提供更直观的参考依据，定性分析同样重要[29]。模糊综合分析来源于模糊数学中的隶属度理论[30]，它能将待评价对象进行定性和定量分析间的相互转换，在风险评价领域有极大的实用价值。对于本研究，模糊综合分析主要分为两步：1）构建模糊评语集；2）构建隶属度函数。

食品风险因子的关键限值是由国家制定的用来判定食品质量是否满足上市要求的统一标准，但单一的限量标准无法对食品质量的潜在风险进行评判，也无法进行多指标的综合评价，例如，某个花生油样品所选取的6 类风险因子均未超标，这并不能说明该样品完全没有风险。因此本研究依据5标度模式[31]，以国家标准为基础设定5 个等级安全风险评语集，即低风险、中风险、警报风险、高风险和极高风险，每个风险等级对应的量化值分别为0.25a、0.5a、0.75a、a和2a，其中a代表国家限量标准，同时也是高风险对应的量化值，对于前4 个风险等级，以等距法设定对应量化值，为突出极高风险的危害性，将其对应量化值设为2 倍的国家限量标准。设立警报风险是由于模糊综合分析的对象是多指标的综合风险评价值，当达到警报风险时说明样品的多个风险因子都十分接近国家限量标准，应该予以重视。

本实验所检测食用油的6 类风险因子均属于负效应类指标，即指标检测值需小于关键限值，适用于降半梯形隶属度函数，对于1.3节中所得第i条综合风险值yi，其隶属度hiq如式（19）～（21）所示。

当q＝1时，

当q＝2,3,4时，

当q＝5时，

式中：Zq表示5标度评价等级所对应的量化值除以国家限量标准后的无量纲值，即{Z1,Z2,Z3,Z4,Z5}＝{0.25,0.5,0.75,1,2}，分别与模糊评语级低风险、中风险、警报风险、高风险和极高风险相对应，计算出第i条综合风险值yi所对应5 个风险等级的隶属度hiq后，根据最大隶属度原则即可判断出食用油所属的风险等级。

2 结果与分析

实验所用计算机为Windows10 64位操作系统，处理器为Intel(R) Core(TM) i5-10400 CPU @ 2.90 GHz，运行内存为32 GB，显卡为NVIDIA RTX 2060（80 W），实验基于Matlab R2015b软件。为了验证本实验提出的基于优化的GRA-ELM风险评价模型的优越性和有效性，将经修改噪声方差后的150 个花生油样本风险指标数据作为模型输入数据，将由式（8）～（10）得到的综合风险评价值作为模型期望输出数据，其中70%作为训练集，30%作为测试集，首先将ELM网络与传统神经网络模型（误差反向传播（error back propagation，BP）、径向基函数（radial basis function，RBF））进行对比以证明ELM网络的泛化能力和鲁棒性，再分别测试滤波模块和PBO算法的有效性。

2.1 不同情况性能对比

2.1.1 不同神经网络性能对比

为了验证ELM网络的泛化能力和鲁棒性，将修改噪声方差后的原始检测数据输入RBF和BP网络模型进行对比实验，统一去掉滤波模块，ELM网络的输入层、隐含层和输出层的节点数分别设为6、20和1，单层BP网络学习率设为0.1，动量因子为0.9，迭代次数为500，激励函数为Sigmoid函数，隐含层节点设为20。RBF网络的学习率设为0.1，迭代次数为500。评判指标为模型预测值与期望值的决定系数（coefficient of determination，R2）和RMSE，分别如式（22）、（23）所示。

GRA-ELM、GRA-RBF和GRA-BP模型回归曲线如图3所示，模型绝对误差曲线如图4所示，GRA-ELM、GRA-RBF和GRA-BP模型性能对比结果如表5所示，图3中期望值曲线是利用式（8）～（10）对测试集样本计算得到的。

表5 GRA-ELM、GRA-RBF和GRA-BP性能对比结果Table 5 Comparative performance of GRA-ELM,GRA-RBF and GRA-BP models

图3 GRA-ELM、GRA-RBF和GRA-BP泛化情况对比Fig.3 Comparison of the generalization results of GRA-ELM,GRARBF and GRA-BP models

图4 GRA-ELM、GRA-RBF和GRA-BP模型绝对误差曲线Fig.4 Absolute error curves of GRA-ELM,GRA-RBF and GRA-BP models

从图3可直观观察到，3 种模型都受到了噪声的干扰，其中BP网络受到的干扰最严重，无法准确地预测风险值。而表5的结果中RBF网络的效果虽略优于BP网络，但从图3中可以看出，RBF的综合风险值中由于噪声的干扰出现了多个负值，是明显的错误值。相比于BP和RBF网络，没有滤波模块的ELM网络虽在一定程度上会受到噪声影响，但其预测值依然能与期望值保持较小的差距，由表5可知，ELM的RMSE以及R2分别为0.132 0、0.796 4，而BP、RBF的RMSE以及R2分别为0.193 8、0.373 8和0.172 0、0.576 2，图4中不同模型绝对误差曲线的对比更进一步说明ELM网络在鲁棒性和泛化能力上的优势。分析其原因，传统神经网络如BP和RBF等会在一次次迭代训练中对数据中存在的噪声进行学习，得到的模型会因为过分学习训练数据中的噪声引起过拟合问题，而ELM网络的输入权值和隐层偏置是随机生成的，与训练数据无关，噪声的影响会低很多。

2.1.2 滤波模块和实用贝叶斯优化算法的有效性

为了验证滤波模块和PBO算法的有效性，对不加滤波模块的模型（GRA-ELM）、加上滤波模块的模型（WT-GRA-ELM）以及再经过PBO后的模型（WT-PBO-GRA-ELM）进行对比实验，以经验法确定的参数与PBO后参数对比如表6所示，模型对比结果如表7所示，模型回归曲线如图5所示，图5中期望值曲线是利用式（8）～（10）对测试集样本计算得到的。

表6 PBO前后的参数对比Table 6 Comparison of parameters before and after PBO

表7 WT-PBO-GRA-ELM、WT-GRA-ELM和GRA-ELM性能对比结果Table 7 Comparative performance of WT-PBO-GRA-ELM,WT-GRA-ELM and GRA-ELM models

图5 WT-PBO-GRA-ELM、WT-GRA-ELM和GRA-ELM泛化情况对比Fig.5 Comparison of the generalization results of WT-PBO-GRAELM,WT-GRA-ELM and GRA-ELM models

由表7可知，加上滤波模块后RMSE达到了0.094 5，相比无滤波时降低了28.41%，R2提升了12.04%，效果明显。从图5中也可看出，加上滤波模块后ELM的拟合度更高，这充分说明滤波模块对于最终风险评价结果准确率的重要性。而经过PBO后，总体性能得到进一步提升，RMSE和R2分别达到了0.056 3和0.946 1。由表6可知，经过PBO算法的参数优化，小波分解后每层高频分量的阈值是不同的，这能够更精确地滤除数据中的噪声。从图5可看出，WT-PBO-GRA-ELM模型对期望值曲线的拟合效果最好，从而说明了PBO算法的有效性。

2.2 风险等级划分结果

针对表1中的食用油原始检测数据，采用式（19）～（21）对本实验所建立WT-PBO-GRA-ELM评价模型输出的综合风险值进行模糊综合分析后，得到的风险隶属度矩阵如表8所示，根据最大隶属度原则可以得出各个样本的风险等级：样本1、3、4、5和6为低风险，样本7为中风险，样本2为极高风险。

表8 风险隶属度矩阵Table 8 Risk membership matrix

以花生油样本2为例，分别对GRA-ELM、WT-GRAELM模型输出的综合风险值进行模糊综合分析，所得风险隶属度如图6所示，GRA-ELM、WT-GRA-ELM模型的风险分级结果都为高风险。而表1中样本2的黄曲霉毒素B1检测结果为20.60 μg/kg，是黄曲霉毒素B1标准限值的2 倍以上，由1.2.4节中国家限量标准倍数对应的风险语言集可知，2 倍标准限值对应的风险语言集为极高风险，同时，样本2其他风险指标检测结果也较为接近标准限值，因此样本2的真实风险等级为极高风险，只有WT-PBOGRA-ELM模型判定结果与真实情况一致，说明本实验所构建的风险评价模能准确识别出食用油风险程度以及优先次序，可以为监管部门制定有针对性的防护策略，并为确立优先监管领域和合理分配风险管理措施资源提供科学依据。

图6 GRA-ELM、WT-GRA-ELM和WT-PBO-GRA-ELM隶属度结果对比Fig.6 Comparison of the membership results of GRA-ELM,WT-GRA-ELM and WT-PBO-GRA-ELM models

3 结论

食用油检测数据具有高维性、复杂性、非线性和离散性的特征，同时，在测定食用油各风险指标含量时可能会出现噪声。本研究在分析国内某食用油主要产出省2017—2019年11 345 行花生油安全日常检测数据及其相关信息的基础上，建立了基于优化的GRA-ELM风险评价模型。首先对指标进行筛选，得到6 类风险指标，再对数据进行预处理，得到150 组样本的花生油检测数据。将预处理后数据输入到小波阈值滤波模块中，对滤波后数据进行GRA，得到指标的权重，并与指标相对风险值结合得到综合风险评价期望值，接着输入到ELM网络中训练，再利用PBO算法进行参数优化。最后对评价模型输出的综合风险值进行模糊综合分析，实现对花生油样品风险程度分级。在不同模型对比实验中，首先通过与BP、RBF网络模型的对比，ELM网络的R2和RMSE分别为0.132 0和0.796 4，性能优于BP网络和RBF网络，证明ELM网络拥有更好的泛化能力和鲁棒性；其次通过对比有无滤波模块以及有无PBO参数优化情况下的结果，最终得出加上滤波模块且进行PBO参数优化后的WT-PBOGRA-ELM模型R2和RMSE分别为0.056 3和0.946 1，证明了滤波模块和PBO算法的有效性；最后通过对比模型评价花生油样本2的结果，得出只有WT-PBO-GRA-ELM模型得到的风险等级结果为极高风险，与该样本真实风险等级一致，证明了本研究风险评价模型的有效性。

未来本研究还可以在以下几个方面更加深入，首先在数据方面，可以将地理因素、时序因素加入模型从而提取出相关风险规律。其次在指标赋权方面，可以将专家打分等主观赋权与危害物本身的毒理学特性和基于数据的客观赋权有机地结合在一起形成更加综合合理的风险因子权重体系。此外，还可以进一步研究对于整条食用油加工链的风险评价。