引信步进应力加速寿命试验无失效数据情况贮存寿命评估
郭华,祝逢春,豆仁福,翟树峰,李敬玉
引信步进应力加速寿命试验无失效数据情况贮存寿命评估
郭华,祝逢春,豆仁福,翟树峰,李敬玉
(北京航空工程技术研究中心,南京 210028)
针对某引信加速寿命试验出现无失效数据情况无评估方法问题,开展贮存寿命评估研究。根据某引信特点和样品条件,选取采用步进应力加速寿命试验。因本次样品量过少,不能进行摸底试验来确定合理的应力和步长,加速寿命试验只能采用其预估值,因而试验结果出现了无失效情况。为此提出先对无失效数据按贝叶斯统计方法将零失效比率(失效数/样本数)数据转换为非降序失效比率的失效数据,再按有失效数据的处理方法评估贮存寿命。以此方法编制计算程序,对某引信无失效试验数据进行处理,评估其贮存寿命为20.1 a。采用贝叶斯统计规律处理无失效数据的方法有效可行,解决了引信步进应力加速寿命试验无失效数据情况下的贮存寿命评估难题。
引信;步进应力;加速寿命试验;无失效数据;不可靠度;贮存寿命;寿命评估
引信贮存寿命评估有基于自然贮存样品试验数据统计评估法和加速寿命试验数据评估法。对于新产品和生产批次少的产品,通常只能采用加速寿命试验来进行评估。加速寿命试验是用以研究产品可靠贮存寿命的一种有效方法。按应力施加方式不同,加速寿命试验可以分为恒定应力加速寿命试验、步进(阶梯)应力加速寿命试验和序进应力加速寿命试验[1],其中步进应力加速寿命试验(简称步加试验)是一种常用方法。在正式进行加速试验前,往往需要进行科学合理的试验设计,以便获得理想的试验数据,取得好的试验效果。良好的试验设计要求每个测试阶段都有产品失效,为达到产品出现失效的要求,最有效的方法是进行摸底试验。对于样品不足的产品,又无条件进行摸底试验,只能靠理论分析或凭借研究经验来确定。这给试验设计带来一定盲目性,因而很可能出现无失效或过多失效现象。在进行某引信步加试验时,由于样品量的不足,无法进行摸底试验来确定合适的加速应力和步长,因而采用预估的应力水平和步长加速,结果出现了无失效或零失效现象。针对这种无失效数据情况的贮存寿命评估,查找了大量的加速寿命试验数据处理方法文献,最相关的有文献[2-19],但这些文献均不涉及利用无失效试验数据评估贮存寿命的方法。为此,本文引入贝叶斯统计方法,优选先验分布密度模型,有效地利用无失效数据评估了某引信的贮存寿命。该贮存寿命评估结果被某研究项目采纳,后经验证符合工程实际。
1 步加试验数据处理方法
正常的步加试验数据的处理或贮存寿命评估方法[20-21]较为成熟。本文方法所不同的是针对无失效数据情况的数据进行处理。本文采用贝叶斯方法,优选先验分布密度模型,将无失效数据情况转换为有失效数据情况,从而按正常数据处理方法来处理数据,评估贮存寿命。
1.1 寿命分布假设
有关数据处理研究表明,引信、弹药贮存寿命符合威布尔分布[20-21]。假设在温度应力T下,产品的贮存寿命服从二参数威布尔分布,即:

式中:m为形状参数;η为特征寿命(真尺度参数)。
在不同温度应力水平T下,存在不同的特征寿命η,η与T之间符合阿仑尼斯模型,即:

式中:和为待定参数。
1.2 时间折算



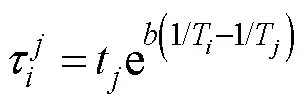
累计得出应力T下产品的实际试验时间为:

1.3 似然方程组

1)似然函数:

式中:为测试子样序数,=1,2,…,;n为每一测试点处样本量;r为每一测试点处的失效数;为威布尔分布形状参数;τ为每一测试点的等效试验时间;η为特征寿命。式中η和τ分别由式(2)、(5)确定。
2)对数似然函数。对式(6)两边取对数,则:

3)似然方程组。对式(7)取偏微分,得似然方程组:

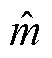
1.4 无失效数据的处理
采用贝叶斯统计方法处理无失效数据,对每个检测点失效比率(不可靠度点估计)作非零非降序处理。对于试验数据,记为:

式中:n、r和c(c=n‒r)分别为t时刻的样本数、失效数和成功数;为检测点总数。
当r=0(=1,2,…,)时,可令:S=n+…+1,(1=1),并令不可靠度1的先验密度[22]为:




式中:S、R和C分别为处理后的样本数、失效数和成功数。
1.5 贮存寿命评估
通过式(2)得出温度应力0时的特征寿命0的估计为:


水源热泵项目取用地下水水资源论证技术要点分析……………………………………………… 江 剑,董殿伟(3.50)
参照式(1),正常贮存条件下的寿命分布函数[23]为:

对于给定置信度=1‒和可靠贮存下限L,则对贮存寿命进行区间估计为:

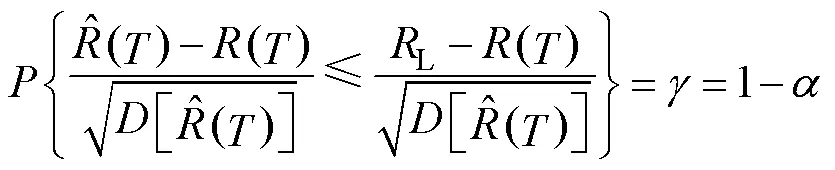
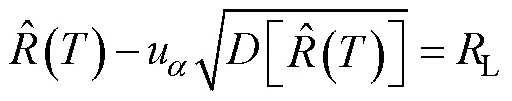
其中:

式中:μ为的下侧分位点;为n或S中的最小者。
2 引信的贮存寿命评估
2.1 试验数据
为评估某引信贮存寿命,笔者进行了引信步进应力加速寿命试验。由于样品严重不足,无法进行摸底试验来确定合理的加速应力和步长,因此通过分析进行了试验设计。在333 K的预估温度应力下,按5 K预估温度步长进行了步加寿命试验,获得某引信步加寿命试验数据,见表1。从表1看出,每个时间测试点失效数均为0(称“零失效”或无失效),即未出现1发失效数据。
表1 引信步加试验数据

Tab.1 Fuze step-stress accelerated life test data
2.2 试验数据预处理
因该引信产品的可靠性较高,预估的加速应力和步长不够合理,加速试验出现了无失效数据情况,因而在正式进行数据处理前,必须对现有无失效数据作预处理。由于作预处理计算时需要起始不可靠度数据,故由某批104枚样本试验零失效的数据按二项分布求出不可靠度上限为0.022(置信水平0.9)。采用1.4节无失效数据情况的数据处理方法,得出无失效数据的预处理结果,见表2。从表2看出,经过预处理的数据变为失效比率非降序的正常数据。
表2 无失效数据预处理结果

Tab.2 Processing results of zero-failure data
2.3 解非线性方程组

2.4 可靠贮存寿命评估
可靠贮存寿命是指一定可靠度下的寿命,因而评估可靠贮存寿命时,首先需要给定可靠度下限,然后再计算此可靠度下限条件下的可靠贮存寿命下限。根据引信的重要性、产品相关要求及用户意见,确定引信可靠度下限L为0.975。根据1.5节的方法,编制Matlab程序,结合式(15)、(19),求解方程(18),对于给定可靠度下限L,计算得出可靠贮存寿命下限L=20.1 a。
3 结语
通过上述数据处理方法和某引信可靠贮存寿命评估实例研究,可得出如下结论:
1)采用贝叶斯方法对无失效数据进行预处理,推断出相应的有失效数据,再按有失效数据的处理方法进行处理,得出可靠度函数,从而可推断出正常应力环境下产品的可靠度及其可靠贮存寿命下限,有效地解决了加速试验无失效数据情况的数据处理难题。
2)采用上述无失效数据情况的数据处理方法,评估某引信可靠度下限为0.975时的可靠贮存寿命下限为20.1 a。这既满足当时引信延寿研究项目的要求,经验证后,又符合工程实际。
贮存寿命结论推断的可信性依赖于试验数据的准确性和加速失效机理的不变性,同时加速模型和失效分布模型正确与否也影响推断结果。因此,在进行加速试验时,施加应力要适度,不能过大而改变失效机理,也不宜过小使试验时间太长或出现无失效情况。本文的数据处理方法只是一种补救方法,有条件要尽量避免无失效数据的情况。在进行数据处理时,也要尽量选定合适的加速模型和失效分布模型。
本文采用的步进应力加速寿命试验,施加应力较小,以至于无一发失效,故不存在改变机理问题。采用的加速模型和失效分布模型是弹药引信常用的,无失效数据处理中采用的先验分布密度模型[25]也是经过验证有效的。因此,可以认为本文的评估方法正确,评估的结果风险有限,结论可信。
[1] 刘松. 武器系统可靠性工程手册[M]. 北京: 国防工业出版社, 1992.
LIU Song. Weapon System Reliability Engineering Manual[M]. Beijing: National Defense Industry Press, 1992.
[2] 胡恩平, 罗兴柏, 艾志利. 三参数威布尔分布条件下的无线电引信步进应力加速寿命试验与数据处理[J]. 探测与控制学报, 2000, 22(2): 37-40.
HU En-ping, LUO Xing-bai, AI Zhi-li. The Step Stress ALT and Data Processing of the Radio Fuze under the Condition of Three-Parameter Weibull Distribution[J]. Journal of Detection & Control, 2000, 22(2): 37-40.
[3] 周虎儿, 张湘平, 徐琰. 基于Powell方法的引信步进应力加速寿命试验数据处理[J]. 探测与控制学报, 2007, 29(2): 27-29.
ZHOU Hu-er, ZHANG Xiang-ping, XU Yan. Data Processing in Fuze Step-Stress Accelerated Life Test Based on Powell Method[J]. Journal of Detection & Control, 2007, 29(2): 27-29.
[4] 赵河明, 张亚, 董少峰. 无线电引信电子头部件长贮加速寿命试验数据处理方法探讨[J]. 探测与控制学报, 1999, 21(4): 33-36.
ZHAO He-ming, ZHANG Ya, DONG Shao-feng. The Study on the Data Processing Method for a Long Term Storage Accelerated Life Test of the Electronic Head Assembly of a Radio Fuze[J]. Journal of Detection & Control, 1999, 21(4): 33-36.
[5] 李道清, 王德元. 某无线电引信加速寿命试验研究[J]. 探测与控制学报, 2000, 22(4): 57-61.
LI Dao-qing, WANG De-yuan. Study on the Long Term Storage Stepping Stress Accelerated Life Test of a Radio Fuze[J]. Journal of Detection & Control, 2000, 22(4): 57-61.
[6] 张生鹏, 李宏民, 赵朋飞. 导弹装备贮存寿命加速试验技术体系探讨[J]. 装备环境工程, 2018, 15(2): 92-96.
ZHANG Sheng-peng, LI Hong-min, ZHAO Peng-fei. Accelerated Testing Technology System for Storage Life of Missile Equipment[J]. Equipment Environmental Engineering, 2018, 15(2): 92-96.
[7] 李敏伟, 傅耘, 王丽, 等. 加速贮存寿命试验设计方法研究[J]. 装备环境工程, 2014, 11(4): 58-64.
LI Min-wei, FU Yun, WANG Li, et al. Study of the Design Method of the Accelerated Storage Life Testing[J]. Equipment Environmental Engineering, 2014, 11(4): 58-64.
[8] 赵方超, 罗天元, 李超, 等. 某型固体云爆剂加速老化试验与贮存寿命预测研究[J]. 装备环境工程, 2011, 8(6): 34-37.
ZHAO Fang-chao, LUO Tian-yuan, LI Chao, et al. Study on the Accelerated Aging Test and Storage Life Prediction of SE-FAE[J]. Equipment Environmental Engineering, 2011, 8(6): 34-37.
[9] 祝逢春, 胡瑜, 游培寒, 等. 基于实际储存使用信息的制导弹药可靠贮存寿命预测[J]. 弹箭与制导学报, 2013, 33(6): 197-199.
ZHU Feng-chun, HU Yu, YOU Pei-han, et al. A Reliable Storage Life Estimation of Guided Munitions Based on Storage and Application Information[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2013, 33(6): 197-199.
[10] 张清爽, 胡双启. X弹头B部件装药贮存寿命研究[J]. 火工品, 2003(1): 26-28.
ZHANG Qing-shuang, HU Shuang-qi. Study on the Storage Life of Explosive Part B in X Warhead[J]. Initiators & Pyrotechnics, 2003(1): 26-28.
[11] 张仕念, 易当详, 宋亚男, 等. 固体推进剂多失效模式相关的贮存可靠性评估[J]. 固体火箭技术, 2007, 30(6): 525-528.
ZHANG Shi-nian, YI Dang-xiang, SONG Ya-nan, et al. Evaluation on Storage Reliability of Solid Propellant Based on Correlative Failure Modes[J]. Journal of Solid Rocket Technology, 2007, 30(6): 525-528.
[12] 李田科, 李建华, 刘炜, 等. 一种基于测试数据的单枚导弹贮存寿命评估方法[J]. 装备环境工程, 2013, 10(6): 88-92.
LI Tian-ke, LI Jian-hua, LIU Wei, et al. A Test Data Based Analysis Method for Single Missile Storage Life Evaluation[J]. Equipment Environmental Engineering, 2013, 10(6): 88-92.
[13] 张福光, 崔旭涛, 洪亮. 导弹火工品贮存寿命的影响因素分析[J]. 装备环境工程, 2011, 8(6): 24-27.
ZHANG Fu-guang, CUI Xu-tao, HONG Liang. Influencing Factor Analysis of Storage Life of Missile Initiating Explosive Devices[J]. Equipment Environmental Engineering, 2011, 8(6): 24-27.
[14] 赵东华, 张怀智, 郭胜强, 等. 基于灰色模型的某型末制导弹药贮存寿命预测[J]. 装备环境工程, 2011, 8(6): 28-30.
ZHAO Dong-hua, ZHANG Huai-zhi, GUO Sheng-qiang, et al. Prediction of Terminal Guided Projectile Storage Life Based on Gray Model[J]. Equipment Environmental Engineering, 2011, 8(6): 28-30.
[15] 黄强, 廉振国, 方延平. 预测弹药装药寿命常用方法的分析[J]. 弹箭与制导学报, 1997, 17(2): 60-62.
HUANG Qiang, LIAN Zhen-guo, FANG Yan-ping. Analysis of Common Methods for Predicting Ammunition Charge Life[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 1997, 17(2): 60-62.
[16] 卢明章, 左英英, 刘所恩. 某型导弹弹射发动机装药的安全贮存寿命预估[J]. 火炸药学报, 2008, 31(1): 72-74.
LU Ming-zhang, ZUO Ying-ying, LIU Suo-en. Safe Storage Life Estimation of a Certain Catapult Missile Motor Charge[J]. Chinese Journal of Explosives & Propellants, 2008, 31(1): 72-74.
[17] 任国周. 固体火箭发动机装药寿命预示方法试验研究[J]. 推进技术, 1996, 17(2): 23-26.
REN Guo-zhou. The Research of Forecast Method for Grain Life in Sold Rocket Motors[J]. Journal of Propulsion Technology, 1996, 17(2): 23-26.
[18] 祝逢春, 刘恒春, 游培寒, 等. TNT基炸药储存寿命评估研究[J]. 爆破器材, 2016, 45(3): 36-41.
ZHU Feng-chun, LIU Heng-chun, YOU Pei-han, et al. Study on Storage Life Assessment of a Composite Explosive Based on TNT[J]. Explosive Materials, 2016, 45(3): 36-41.
[19] 余文力, 董三强, 朱满林, 等. 导弹战斗部炸药装药的贮存可靠性研究[J]. 空军工程大学学报(自然科学版), 2005, 6(2): 43-45.
YU Wen-li, DONG San-qiang, ZHU Man-lin, et al. Research on Storage Reliability of Missile Warhead Explosive Charge[J]. Journal of Air Force Engineering University (Natural Science Edition), 2005, 6(2): 43-45.
[20] GJB 5103—2004, 弹药元件加速寿命试验方法[S].
GJB 5103—2004, Accelerated Life Test Method of Ammunition Components[S].
[21] 卢秋红, 董少峰, 张亚. 弹药步进应力加速寿命试验数据处理方法探讨[J]. 探测与控制学报, 2000, 22(1): 47-50.
LU Qiu-hong, DONG Shao-feng, ZHANG Ya. The Study on the Data-Processing Method of Ammunition Stepstress Accelerated Life Tests[J]. Journal of Detection & Control, 2000, 22(1): 47-50.
[22] 徐振相, 秦士嘉. 火工品可靠性技术: 基础与管理[M]. 北京: 兵器工业出版社, 1996.
XU Zhen-xiang, QIN Shi-jia. Reliability Technology of Initiating Explosive Device: Foundation and Management[M]. Beijing: The Publishing House of Ordnance Industry, 1996.
[23] 李明伦, 李东阳, 郑波. 弹药储存可靠性[M]. 北京: 国防工业出版社, 1997.
LI Ming-lun, LI Dong-yang, ZHENG Bo. Ammunition Storage Reliability[M]. Beijing: National Defense Industry Press, 1997.
[24] 郑波, 葛广平. 基于步进应力加速寿命试验的引信贮存寿命评估[J]. 北京理工大学学报, 2003, 23(5): 545-547.
ZHENG Bo, GE Guang-ping. Estimation of Fuze Storage Life Based on Stepped Stress Accelerated Life Testing[J]. Journal of Beijing Institute of Technology, 2003, 23(5): 545-547.
[25] 祝逢春, 王晓鸣, 崔大伟, 等. 弹药可靠性试验逆序数据的统计修正[J]. 弹箭与制导学报, 2006, 26(3): 135-136.
ZHU Feng-chun, WANG Xiao-ming, CUI Da-wei, et al. Statistic Amendable Method of Reverse Order Data of Ammunition Reliability Test[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2006, 26(3): 135-136.
Evaluation of Storage Life of Fuze via Step-stress Accelerated Life Test with Zero-failure Data
GUO Hua, ZHU Feng-chun, DOU Ren-fu, ZHAI Shu-feng, LI Jing-yu
(Beijing Aeronautical Technology Research Center, Nanjing 210028, China)
The work aims to study the storage life evaluation to solve problem of zero-failure data and no evaluation method in accelerated life test of a fuze. According to the characteristics and sample conditions of a certain fuze, step-stress accelerated life test was performed. Because the sample size was too small, it was impossible to carry out a fundamental test to determine the rational stress and step length, and the accelerated life test can only use its estimated value, so the test result showed zero-failure. In order to solve this problem, the data zero-failure ratio (number of failures/number of samples) was converted into failure data of non-descending failure ratio according to the Bayesian statistics method. Then the storage life was evaluated according to the processing method with failure data. The calculation program was compiled with this method to process the zero-failure test data of a fuze, and the estimated storage life was 20.1 years. The results of a fuze storage life evaluation show that the method of using Bayesian statistical law to deal with zero-failure data is effective and feasible, and solves the problem of the fuze storage life evaluation under the condition of zero-failure data in step-stress accelerated life test.
fuze; step-stress; accelerated life test; zero-failure data; unreliability; storage life; life evaluation
2020-01-22;
2022-05-05
GUO Hua (1978-), Female, Doctor.
TJ410.6
A
1672-9242(2023)02-0026-06
10.7643/ issn.1672-9242.2023.02.004
2022–01–22;
2022–05–05
郭华(1978—),女,博士。
祝逢春(1964—),男,博士。
Corresponding author:ZHU Feng-chun (1964-), Male, Doctor.
郭华, 祝逢春, 豆仁福, 等. 引信步进应力加速寿命试验无失效数据情况贮存寿命评估[J]. 装备环境工程, 2023, 20(2): 026-031.
GUO Hua, ZHU Feng-chun, DOU Ren-fu, et al.Evaluation of Storage Life of Fuze via Step-stress Accelerated Life Test with Zero-failure Data[J]. Equipment Environmental Engineering, 2023, 20(2): 026-031.
责任编辑:刘世忠

