考虑退货影响的概率销售下的库存问题研究

吴茜茜, 赵慧慧, 郝晶晶

(1.合肥工业大学 数学学院,安徽 合肥 230601; 2.合肥工业大学 经济学院,安徽 合肥 230601)

0 引 言

对于销售商来说,随着市场竞争越来越激烈,采取正确的销售策略十分重要,其中概率销售这一策略已逐渐得到大家的认可。文献[1]首次提出概率销售的概念,它是指销售商利用现有的产品进行包装组合以创造出一种概率产品,并将它作为另一种购买选择;而这类产品的特点是消费者收到产品时才能获得其所有的信息。例如,由多种产品组成的“盲袋”可看作是概率产品,顾客购买时只有拆开“盲袋”才知道产品的款式、颜色等具体信息。现在越来越多的研究开始关注概率销售在零售市场的应用,寻找影响其库存决定和期望利润的因素,比如产品上架的时间、产品间的需求相关性和需求不确定大小等[2-3]。文献[4]通过数值结果说明,与只在实体渠道销售传统产品的传统销售相比,概率销售同时在实体渠道销售传统产品和网络渠道销售概率产品的收益更高。通过将概率销售视为一种库存管理工具,文献[5]发现,当产品的差异越大以及顾客的敏感度水平越高,卖家采用概率销售策略后更有优势;文献[6]讨论了卖家采用概率销售时可以通过适当的折扣进行有效的库存管理。

在产品的销售过程中,顾客退货这一行为是很常见的,考虑退货对销售商的销售决策具有实际意义。文献[7]利用销售商和制造商共同构建的供应链模型,讨论了产品的最优退货价格、订购量和利润等有关情况;文献[8]假设退货量与市场需求成比例,认为在竞争激烈的市场中,退货这一行为必定会影响产品的订货策略,以及控制退货率是有利于提高企业的利润收入的。目前,绝大多数文献都是针对传统销售模式研究产品的退货情况以及探讨其对库存管理的影响。而在无理由退货政策的支持下,通过建立Hotelling模型,文献[9]探讨了概率销售策略中概率产品和传统产品的组合方式以及消费者满意度对利润的影响。

在面对库存管理问题时,卖家一直都在致力于化解订购量与需求量之间的矛盾。为能更好地降低损失以及实现更加有效的库存管理,除了采用概率销售策略外,还可以通过引入贝叶斯信息更新方法预测产品订购量,从而降低产品需求的不确定性,改善销售商的利润收入[10-13]。贝叶斯信息更新如今已被广泛运用于零售策略中。文献[14]通过研究多种产品投放方式的库存问题,发现零售商根据市场观察结果,运用贝叶斯方法修正需求分配的现有信息,并根据动态规划得到最佳的订货策略;文献[15]利用贝叶斯信息更新下的报童模型获得最优库存方式,并分析购买成本和市场需求信息对库存决策的影响。

在考虑商品退货的政策下,本文结合贝叶斯信息更新,探讨概率销售模式下产品的最优库存量和期望利润。首先介绍退货函数以及贝叶斯信息更新过程;然后得到基于贝叶斯信息更新的最佳库存和期望利润的函数;最后通过数值模拟分析不同情况下顾客的退货率以及概率产品的转换率对库存水平的影响。

1 假 设

在概率销售中,考虑卖家销售产品(i,j,k)(其中产品k为概率产品,由传统产品i和j组合而成)。假设产品i和j的销售价均为p,产品k的价格为pk(pk=(1-r)p,r为折扣率),成本均为c,清仓价均为s。在传统销售中,考虑产品i和j的市场需求量是随机的,设为(di,dj)。由于概率产品k是由产品i和j组合而成,在概率销售过程中,该产品的需求量随着产品i和j相应地发生变化。假设有ai(aj)(转换率)的顾客是原先欲购买产品i(j)而转移去购买了概率产品k,则最终概率销售下产品(i,j,k)的需求量(Di,Dj,Dk)满足:

Di=(1-ai)di,Dj=(1-aj)dj,

Dk=aidi+ajdj

(1)

卖家一方面要面对需求不确定的问题,另一方面还要考虑产品退货带来的影响。假设产品的退货量与市场需求量成比例,记为R=αD,其中α称为退货率。由于市场需求量D是随机的,根据产品库存量Q,有

(2)

2 模 型

2.1 贝叶斯信息更新

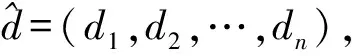
(3)

根据贝叶斯定理

(4)

并且在共轭分布的支持下,最终得到更新后的后验:

(5)

在具体的销售过程中,通过对产品i的需求量分布进行贝叶斯信息更新,最终获得产品j的需求量dj分布为:

dj～N(μ1(n),d1(n)+σ)

(6)

(7)

(8)

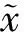
2.2 库存决定

对于产品i和j,若顾客在不满意的情况下退货(而由于概率产品的特殊性质,规定产品k不能进行退货),卖家在收到退货产品后,将以清仓价进行处理。假设产品i和j退货数量为Ri(Rj),可得到关于库存量(Qi,Qj,Qk)的期望利润函数:

π(Qi,Qj,Qk)=

pRi+sRi-cQi+

pmin(Dj,Qj)+s(Qj-Dj)+-

pRj+sRj-cQj+

(9)

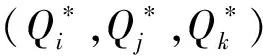
(10)

因此有:

(11)

而对产品j和k,同样可以得到最佳库存量为:

(12)

(13)

其中:φ(x)为标准正态分布;

(14)

(15)

为计算简单,假设μ1(n)=μ0。将(11)～(13)式分别代入(9)式,进一步获得最佳期望利润为:

(αp-αs-rp)(ai+aj)μ0-

[(1-r)p-c]φ[φ-1(γ)]}

(16)

其中,φ(x)=φ′(x)。产品组合(i,j,k)的最佳库存总量为:

(17)

因此,在考虑产品退货问题的情况下,可以根据(16)、(17)式获得贝叶斯信息更新下概率销售的最佳库存量及其对应的期望利润。接下来,将通过数值模拟,具体分析退货率α以及产品间转换率a的取值对于库存决定的影响。

3 数值模拟

本节基于贝叶斯信息更新过程,首先对比产品退货率对不同销售模式下库存决策影响的差异,然后研究概率销售中退货率α以及产品转换率a不同时,最佳库存量和期望利润的变化情况。设p=100,c=60,s=50,r=0.001,μ0=100,σ=50,d0=20,ai=aj=a=0.1。

3.1 退货率的影响

根据2.2节销售方式的库存决策函数,假设信息更新过程中的样本信息量为n=50,最佳库存量和期望利润的变化趋势如图1所示,图1展示了退货率对传统销售和概率销售2类销售策略的影响。

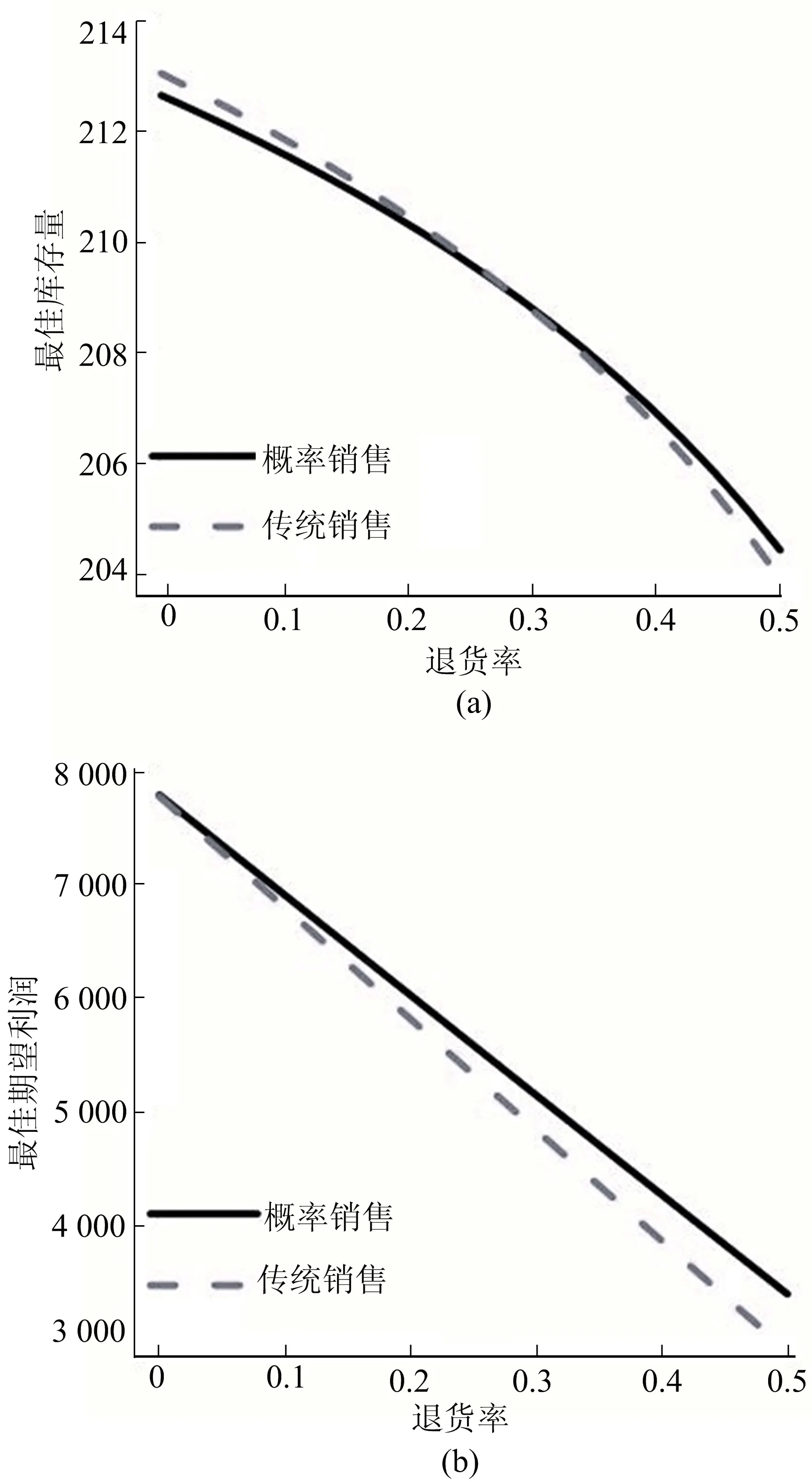
图1 贝叶斯更新下概率销售和传统销售的库存决定比较

由图1可知,引入贝叶斯信息更新后,不论是采用概率销售还是传统销售,卖家的最理想情况是顾客没有退货(α=0),此时利润最大。而随着α的增大,2类销售策略下的最佳库存量和期望利润均在减小。另外,由图1b可知,不论α取值多少,概率销售策略下的最佳期望利润始终高于传统销售情况下的利润,并且它们之间的差距随着α的增大而增大。

结合图1a可以看出,当退货率较低时(如α<0.2),相较于传统销售,概率销售可以用更低的最佳库存量获得更高的最佳期望利润;但随着α逐渐增大(如α>0.4),传统销售的最佳库存量更低,但其最佳期望利润也更低。

总的来说,从图1可以看出,在面对常见的退货问题时,销售商可以通过采用概率销售策略减少损失,这一结论也适用于信息量n取其他任意值的情况。

下面将重点围绕概率销售这一策略下的库存管理问题进行分析和讨论。首先,观察在不同信息量(n=0、5、30、50、100)的情况下,退货率对最佳库存量和期望利润的影响如图2所示。

在进行最佳库存量比较时,从图2a和图2c可以看出,引入贝叶斯信息更新过程的概率销售所获得的最佳库存量更低。但从图2b可以看出,在不同n值下最佳期望利润几乎吻合，说明贝叶斯信息更新方法的引入且拥有较多信息量时,可以以较低的库存量达到同等预期的收益。

图2d进一步说明了对应的利润差距,α越大,利润差越小。另外,从图2c和2d可以看出,随着样本信息量的增加,最佳库存量和期望利润的差距均在增加;但当信息量达到n=30后,更多的信息量都无法明显地影响库存量决定以及期望利润。

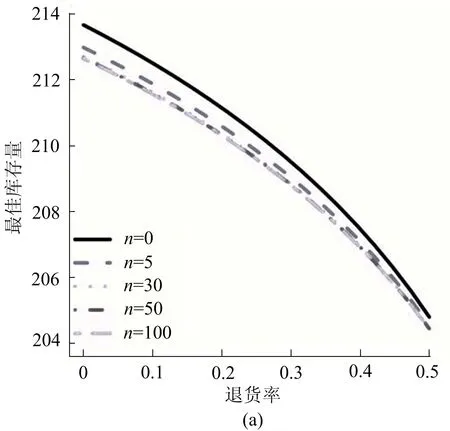
图2 不同n值下概率销售的库存决定比较

3.2 概率产品转换率的影响

本文已通过数值模拟研究贝叶斯信息更新过程中退货率这一单因素对不同销售策略中库存管理水平的影响,而在概率销售中,概率产品的转换率(假设ai=aj=a)也会影响库存决定。退货率和转换率共同作用后对概率销售的最佳库存量和期望利润的影响如图3所示。由图3可知,针对较低的产品退货率(如α<0.1),当转换率增大时,最佳库存量和利润都会降低，顾客对概率产品需求量大而使得正价产品需求降低,导致商家的利益受到损失;反之,当产品的退货率较高(如α>0.4),随着转换率的上升,最佳库存和期望收益也会升高。由图3b可知,当产品的退货率较高时,概率产品的出现可以帮助卖家降低退货带来的损失;而较大的需求量则需要更多的库存量来支持,从图3a可以看出,当退货率逐渐增大时,库存量随着概率产品需求的提高而增大。

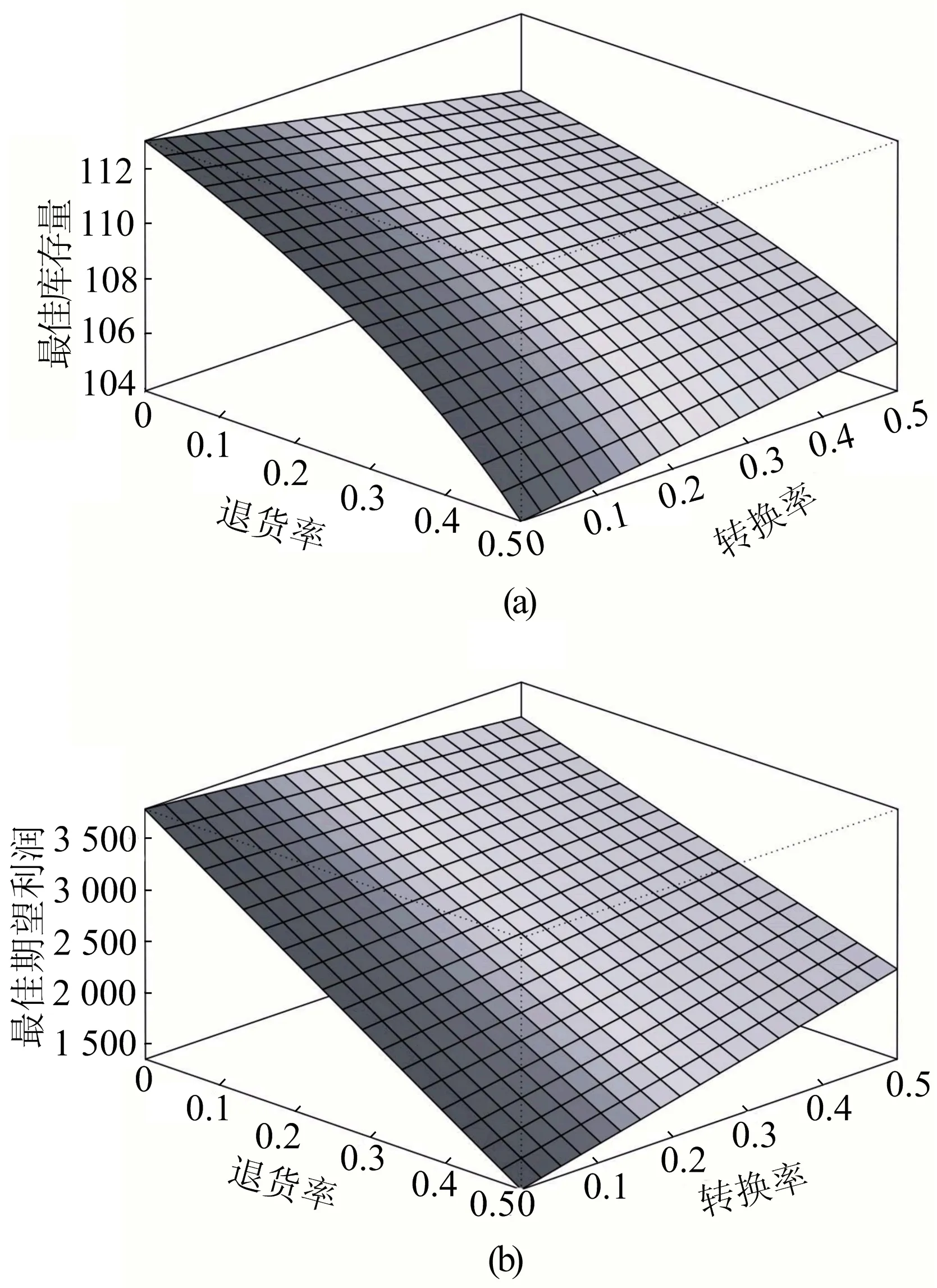
图3 贝叶斯信息更新下退货率和转换率对概率销售的影响

4 结 论

面对竞争激烈的销售市场,卖家不仅需要对产品的库存管理进行决策,还要面对顾客退货带来的压力。本文将贝叶斯理论与概率销售相结合,研究退货问题对贝叶斯信息更新下的概率销售的库存管理的影响。研究结果表明,在退货问题的影响下,相较于传统销售,概率销售的库存管理更有优势。另外,采用贝叶斯信息更新下的概率销售的库存管理水平更佳,即贝叶斯信息更新可以降低退货带来的损失。与此同时,产品信息量的增加可以在一定范围内帮助提高收益,并且随着产品退货率的升高,概率产品的需求量越高,退货造成的损失也会降低。本文主要从销售商的角度出发,计算其期望收益;未来在考虑概率销售的退货问题时,还可以从顾客的角度出发,例如退货后顾客对产品的价值估计变化以及支付退货运费等对其利益的影响,然后通过对比买、卖双方的利益变化,做出最优库存决策。