大跨度体育馆风效应的大涡模拟及风洞试验的对比研究

郅伦海, 程 磊, 孟 磊, 刘毛方

(1.合肥工业大学 土木与水利工程学院,安徽 合肥 230009; 2.安徽省金田建筑设计咨询有限责任公司,安徽 合肥 231600)

因为大跨度屋盖结构的自重轻、阻尼小、柔度大,自振周期与风速的卓越周期接近[1],通常位于大气边界层中风速变化大、湍流度高的近地区域,主要受到气流的分离和再附流作用[2],所以大跨度屋盖结构对风荷载极其敏感。大跨度屋盖结构的风荷载特性不仅与结构造型有关,还与所处的建筑环境有关。周边群体建筑分布愈加密集,大跨度屋盖结构受到的遮挡效应和狭缝效应会愈加显著[3]。现场实测和风洞试验数据显示,在大跨度屋盖迎风前端,气流分离现象严重,脉动风压极值会达到平均风压的3.5倍以上[4],其影响十分严重。因此有必要开展群体布局下大跨度屋盖结构平均风压及脉动风压的研究。

本文以合肥某大跨度体育馆为工程背景,利用计算流体动力学软件Fluent,采用大涡模拟(large eddy simulation,LES)湍流模型,基于随机湍流生成法得到入口脉动风速,对体育馆主副两馆进行风荷载模拟,计算并分析主馆表面的平均风压系数及脉动风压系数分布特性,并将计算结果与风洞动态测压试验进行对比。结果表明数值模拟较好地反映了群体布局下主馆表面风压分布特性,得到的风压系数与风洞试验数据有较好的吻合。本文方法和研究结果对于确定群体布局下,复杂体型的大跨屋盖结构屋面的风荷载具有一定的工程意义和科学价值。

1 工程概况

该大跨体育馆由主馆和副馆组成,如图1所示。副馆南北方向跨度为52.0 m,东西方向跨度为103.5 m,屋盖侧立面由四边形与三角形构成,屋面由倾斜的四边形屋面板拼接而成,相邻屋面板空隙处由三角形屋面板封闭,屋面最高点标高为29.0 m,最低点标高为23.5 m;主馆南北方向跨度为130.5 m,东西方向跨度为103.5 m,屋盖构造与副馆相同,屋面标高为35.0 m。主馆与副馆之间水平最短距离为10.0 m。体育馆东面无遮挡,北面、西面、南面存在较多高低层建筑,其中最高建筑高达75.0 m。合肥市50 a重现期基本风速为 27.1 m/s,按 C类地貌考虑。

图1 建筑效果图

2 大涡模拟数值风洞计算

2.1 控制方程

大涡模拟采用空间过滤方法,分离湍流流场中的大尺度涡和小尺度涡;对大尺度涡,采用直接模拟直接计算;对小尺度涡,采用亚格子模型来模拟其对流场的影响。过滤后的连续性方程和Navier-Stokes方程式如下:

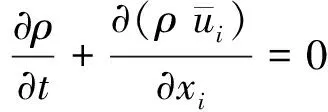
(1)

(2)

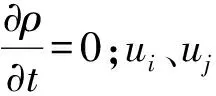
2.2 计算模型及网格划分

数值风洞计算几何建模时按1∶1实际尺寸建模,考虑周围900 m内建筑群,建立体育馆群体模型,几何模型如图2所示。文献[5]表明,当计算域阻塞率小于3%时,可以忽略计算域边界对建筑表面风压分布的影响,阻塞率ω计算公式为:

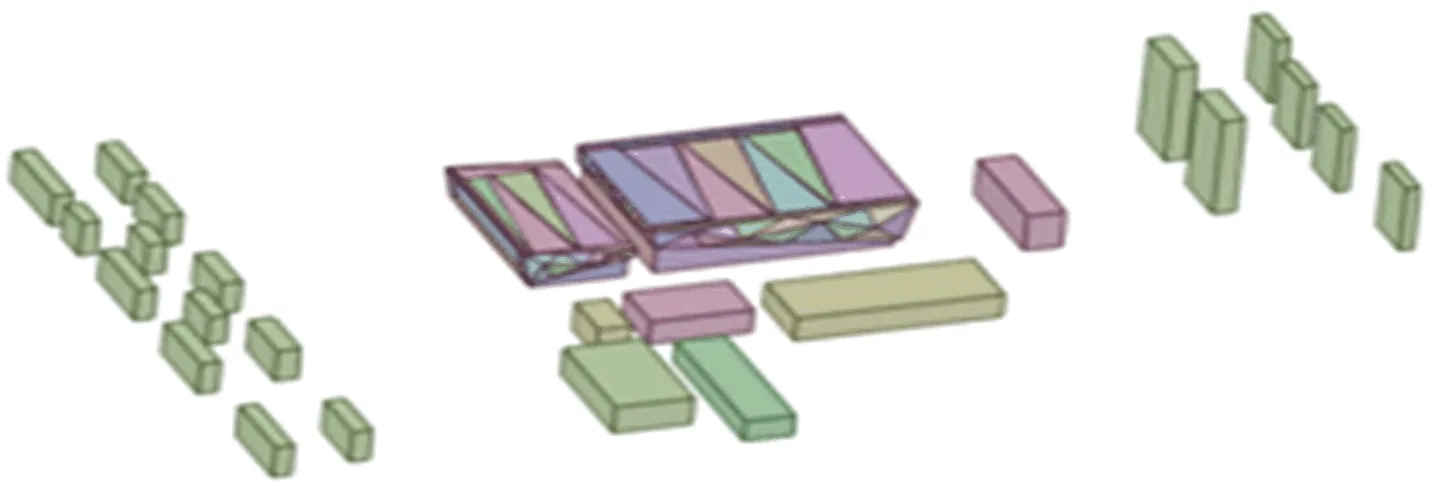
图2 体育馆群体模型

ω=(A0/A1)×100%

(3)

其中:A0为建筑物最大的迎风面积;A1为计算域界面的面积。

基于以上要求,并考虑数值模拟准确性和模拟计算成本,经多次试算后,确定计算域尺寸为x×y×z=2 000 m×3 500 m×300 m,经过计算,最大阻塞率为0.6%,满足要求。为提高计算效率,将整个计算域分成2个部分:一部分为外围区域,其形状规整;另一部分为核心区域,包含体育馆模型及周边建筑,如图3所示(单位为m)。模拟不同风向角来风工况时,将外围区域旋转相应角度,即可建立该工况下数值模型。针对不同风向角工况,分别进行网格划分。

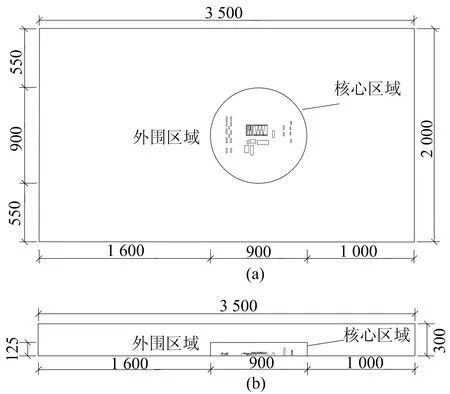
图3 计算域示意图

由于该大跨度体育馆造型复杂,特别是屋面凸起部分存在尖角,难以在计算域中生成高质量六面体结构化网格。为正确模拟大气边界层的风场特性,获得气流撞击复杂造型屋盖后的流动现象;划分高质量网格,提高计算效率;故在Fluent Meshing中,采用多面体网格对整个计算域进行网格划分。在网格划分前,先在建模软件Space Claim中将核心区域与外围区域的交界面、交界线共享拓扑,使2个计算域的交界面、交界线在网格划分时共节点,提高数据传递效率和计算收敛性,交界面在Fluent中自动识别为internal。外围区域形状规整,采用较大尺度网格进行划分,面网格尺寸为1～20 m;核心区域形状复杂,采用较小尺度网格进行划分,裙房面网格为1～5 m,各风向下,体育馆表面网格最小尺寸为0.05 m,最大尺寸为0.30 m。总体网格数量为6×106左右。在体育馆表面生成3层贴体棱柱体网格,第1层壁面网格高度取0.001 m,网格尺寸增长率为1.2,最大网格歪斜度为0.75。文献[6]证明了高雷诺数瑞流下LES壁面函数对近壁面处理的正确性。本文体育馆近壁面y+值为3.5～95.0，在对数率区域内,使用壁面函数对近壁面进行处理,使近壁面满足LES湍流模型的要求,保证模拟结果的准确性。

2.3 边界条件

入口边界采用速度入口(velocity-inlet)。根据文献[7],大气边界层内风速随高度变化规律采用指数律风剖面来描述,即

vz=v0(z/z0)α

(4)

其中:vz为任意高度z处的平均风速;v0为标准高度处的平均风速;z为建筑物计算位置离地面的高度;z0为标准高度,取10 m;α为地面粗糙度指数,在C类地貌条件下,取值为0.22。

通过湍动能k和湍流耗散率ε来确定入口处湍流边界条件,由等效边界层假设[1]给出表达式,即

k(z)=1.2[I(z)vz]2

(5)

(6)

其中:Cμ为模型常数,取值为0.09;K为卡门常数,取值为0.4;I、Lu分别为湍流强度和湍流积分尺度。参考文献[8],I、Lu的计算公式分别为:

(7)

Lu=100(z/30)0.5

(8)

其中:zb=5 m;zB=350 m。

入口湍流通过Spectral Synthesizer[9-10]方法生成,由于计算域出口距离建筑物足够远,可认为出口处尾流已充分发展,出口边界采用自由出流边界(outflow),流场变量散度为0;计算域的顶面和侧面采用对称边界(symmetry),在Fluent中对称边界即无壁面剪应力的自由滑移壁面;地面和建筑物表面采用壁面条件(wall),为无滑移光滑壁面。

2.4 求解参数设置

在数值求解中,认为空气是不可压缩流体。采用WMLES亚格子模型对N-S方程进行求解,计算离散方程组采用分离式解法中的SIMPLEC算法来求解。为保证数值离散精度,动量方程中的对流项采用数值耗散低的二阶中心差分格式,时间项采用二阶隐式格式。为加快数值模拟计算收敛,在进行非定常大涡模拟计算前,先采用RANS模型进行定常计算,并把计算结果瞬态化处理,作为LES的初始流场。LES计算的时间步长取0.05 s,相当于20 Hz的采样频率,能正确反映实际脉动风压特性,共进行10 000步的LES非定常计算。

3 数值模拟结果分析

大跨度体育馆为封闭结构,结构表面某i点的风压系数计算公式为:

(9)

结构表面点i处的平均风压系数的计算公式为:

(10)

同时由(9)式、(10)式可得,结构表面点i的脉动风压系数均方根为:

(11)

其中:Cpi(t)为试验模型上第i个测压孔所在位置的风压系数;pi(t)为该位置上测得的表面风压值;p0、p∞分别为参考点处测得的平均总压和平均静压,参考点高度取45 m处;tm为某一时刻;N为时域点数。

模拟时将正北方向定义为0°风向,逆时针旋转,每隔15°为一个试验工况,共24个试验工况，如图4所示。限于篇幅,本文仅给出0°风向角工况下数值模拟结果。

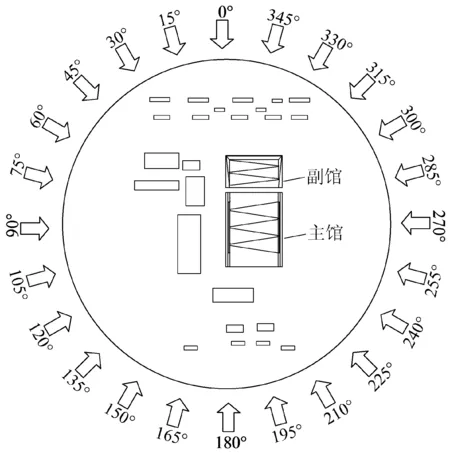
图4 风向角示意图

3.1 平均风压系数

主馆表面平均风压系数分布如图5所示。经仔细研究0°风向角工况下主馆表面数值模拟结果,可以得到如下结论:

(1)主馆北立面(迎风面)由屋盖部分和主体部分组成。屋盖部分以正压为主,主要受压力影响。屋盖形状对风压影响较大,当来流遇到棱角部位,会发生流动分离,形成离散的漩涡,使局部的压力增大。由于屋盖形状不对称,屋盖下部东侧倾斜率大于西侧,流动分离现象更严重,导致屋盖东侧平均压力系数大于西侧。屋盖部分表面最大平均风压系数为0.3,位置出现在屋盖东侧上部。由于副馆的存在,对主馆起到遮挡作用,且气流经过副馆会发生流动分离,在主馆、副馆之间形成漩涡致使北立面主体部分平均风压系数呈上下对称分布,中部以负压为主,平均风压系数达到-0.1。

(2)主馆整体造型大致对称,东西立面形状相同,平均风压系数分布规律相同,均为负值。气流在东西立面前端发生分离,平均风压系数沿立面方向递减,最大负压系数发生在立面前端,值为-0.5。平均风压系数等值线基本垂直于气流流动方向,立面前端等值线密集,平均风压系数变化梯度较大;沿立面方向,平均风压等值线逐渐稀疏,变化梯度逐渐减小。

对比东西立面平均风压系数分布云图可以发现,由于主馆西侧存在建筑群,气流流经时会发生绕流,对主馆西面风压产生影响,致使西面平均风压系数绝对值略大于主馆东面。

(3)主馆南立面(背风面)的风压以负压为主。虽然主馆造型大致对称,但由于西面建筑群的存在及气流的绕流作用,南立面风压系数并不是对称分布。平均风压系数绝对值由西至东逐渐减小,由负变正。最大负平均风压系数出现在凹进部分西侧,值为-0.4;最大正平均风压系数出现在凹进部分东侧,值为0.05。

(4)主馆顶面的风压以负压为主,整体上平均风压系数绝对值沿来流方向递减,等值线逐渐变稀疏,变化梯度逐渐减小。最大负平均风压系数出现在屋盖顶面前缘,值为-0.55。由于屋面上存在凸起部分,当气流流经时,会发生明显的流动分离及回流现象。流动分离会使凸起部分后方形成较大的负压区,最大负压系数为-0.5;回流会使屋面凸起部分前方压力系数由负变正,最大正压系数为0.05。

(5)由规范类同体型的体型系数反推得到主馆表面平均风压系数,迎风面为0.625,侧风面为-0.547,背风面为-0.390,屋面为-0.469;模拟结果整体上略小于规范值,在屋盖前端及凸起部位气流分离严重,数值模拟结果大于规范值。

3.2 脉动风压系数

脉动风压系数反映体育馆表面湍流特性,其大小及分布特征受到来流湍流特性和漩涡脱落特性等因素影响。主馆表面的脉动风压系数分布云图如图6所示。

从图6可以看出:

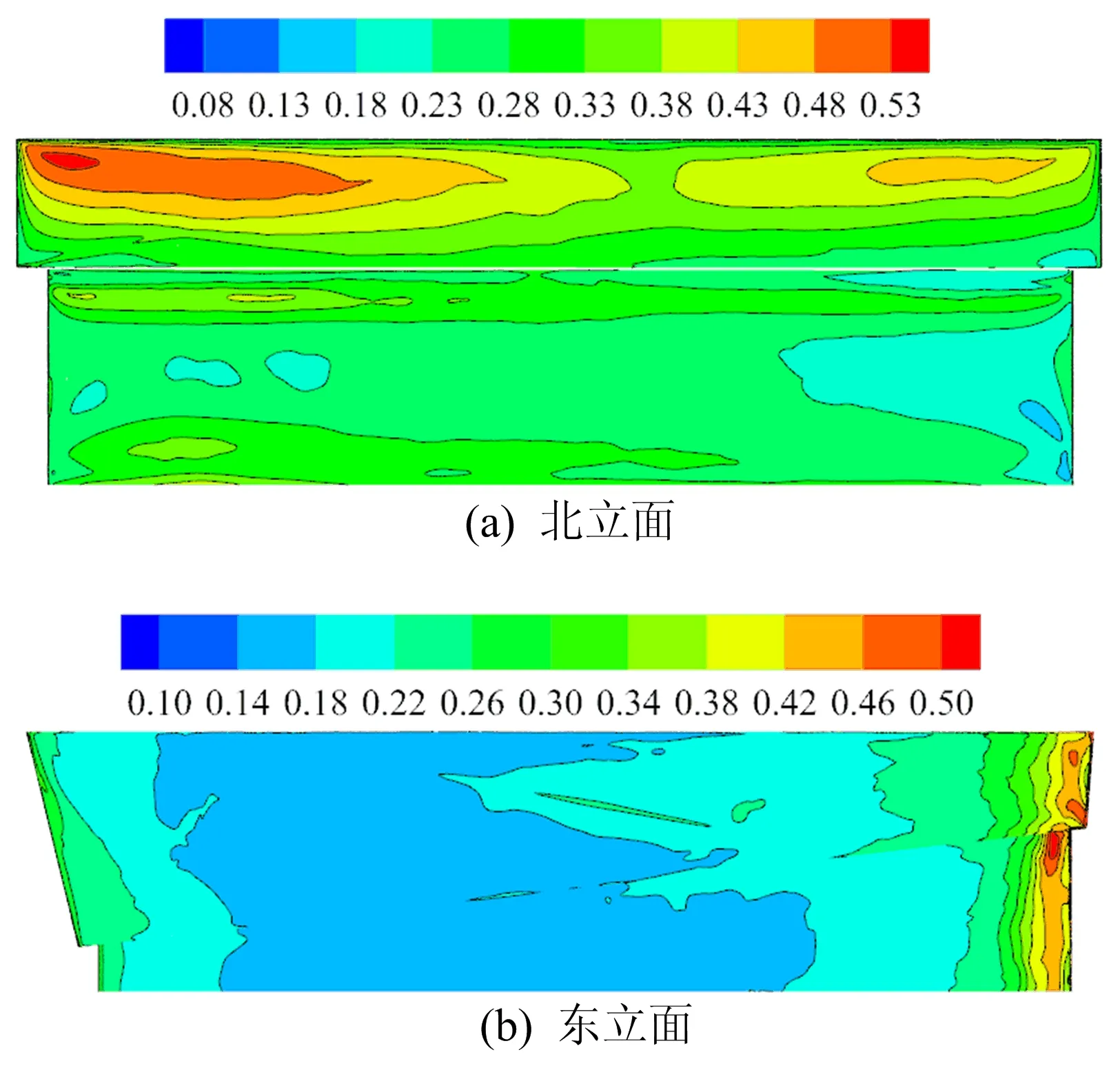
图6 主馆表面的脉动风压系数分布云图

(1)主馆北、东、西立面的脉动风压系数分布规律与平均风压系数分布规律相似,但脉动风压系数等值线分布更加复杂,这是受到来流中的湍流成分影响造成的。

(2)来流在顶面前端迎风边缘发生分离、附着现象,因此整体上顶面前端脉动风压系数大于顶面后端,前端的脉动风压系数的变化梯度大于后端;在屋面凸起部分,气流流动分离现象严重,因此顶面凸起部位脉动风压系数急剧增大。

(3)因为主馆造型整体上对称,所以南立面脉动风压系数分布大致对称;因为体育馆西侧、西南侧建筑群的干扰作用,所以南立面西侧脉动风压系数略大于东侧。

4 数值模拟与风洞试验对比

4.1 风洞试验

该大跨度体育馆项目的风洞试验在湖南大学进行,采用HD-3直流式矩形截面边界层风洞进行高速试验。体育馆模型是由ABS板制成的刚体模型,模型缩尺比为1∶150,高度为23.3 cm,如图7所示。为了测得体育馆主馆表面的风压分布,在模型4个立面及顶面布置了309个测点,如图8所示。试验工况与数值模拟一致,以北面来风定义为0°风向,逆时针旋转,每隔15°为一个工况,共24个工况,风向角示意图见图4。

图7 风洞试验模型

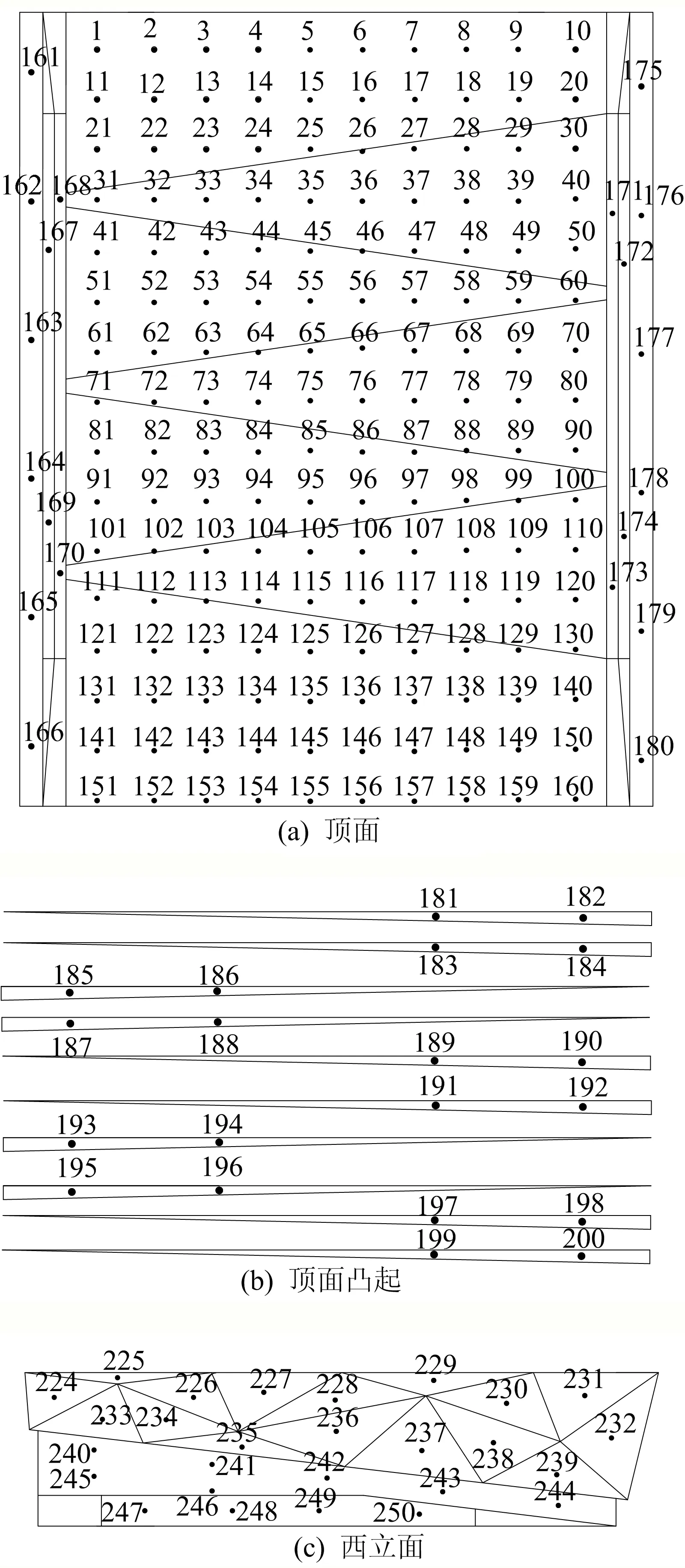
图8 各测点布置

该体育馆周边建筑密集,为C类地貌[7],即α=0.22。为模拟C 类地貌的大气边界层流场,在建筑模型前方设置尖塔阵和粗糙元。在测压模型风洞试验中,为保证试验的准确性,应准确模拟平均风速、风的湍流强度及其积分尺度等,风洞试验的风速剖面及湍流度剖面如图9所示。

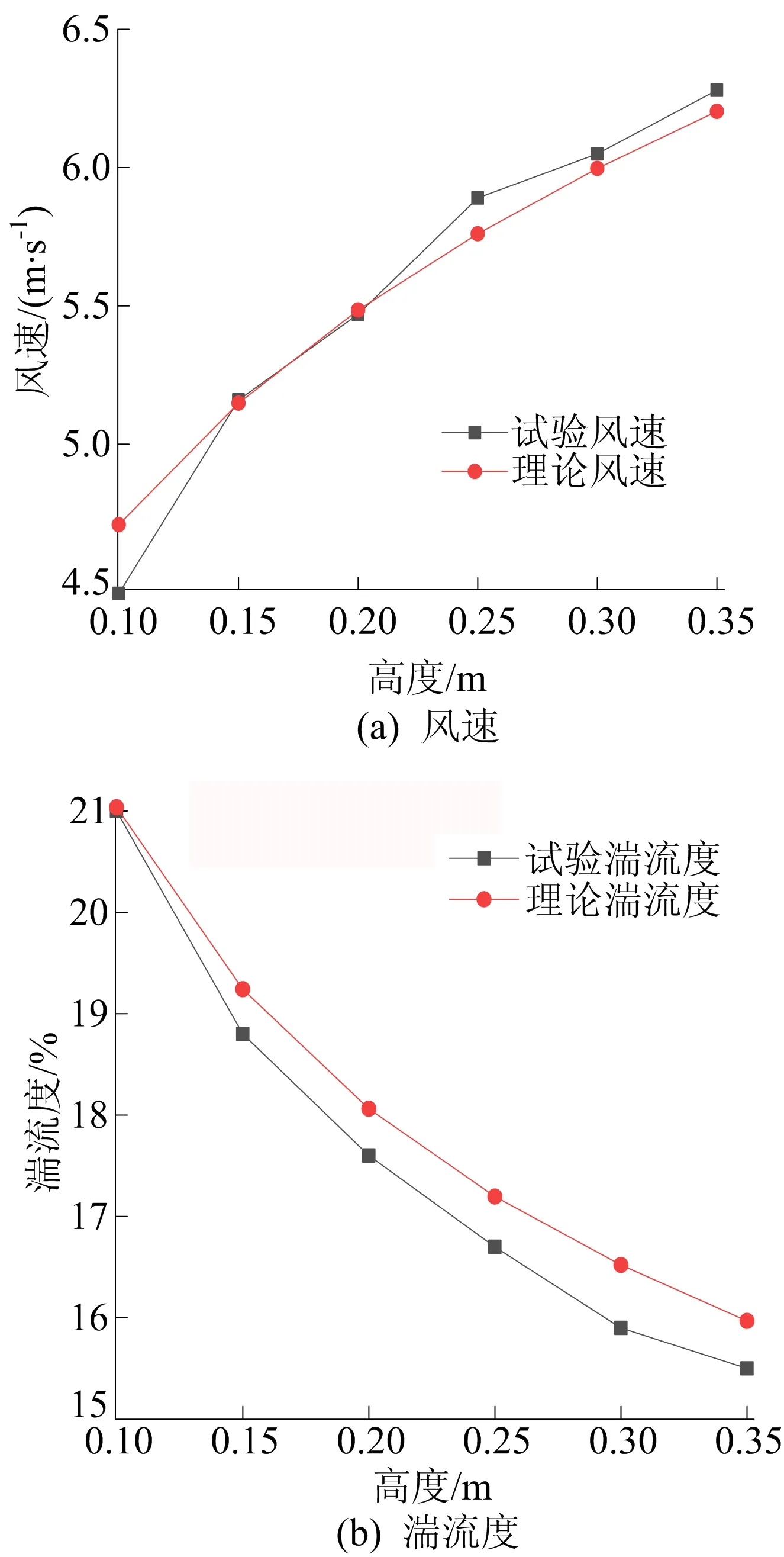
图9 风洞试验的风速剖面及湍流度剖面

在大气边界层中,平均风速剖面符合指数分布律,其中参考高度zref=0.3 m的风速vref=10 m/s,湍流强度自下而上逐渐衰减,在近地面达到最大值。

4.2 平均风压系数对比

在体育馆主馆迎风面、背风面各选取4个典型测点,2个侧风面各选取4个典型测点,顶面选取8个典型测点,共计24个测点进行分析,并与风洞试验结果进行对比,各测点平均风压系数对比如图10所示。

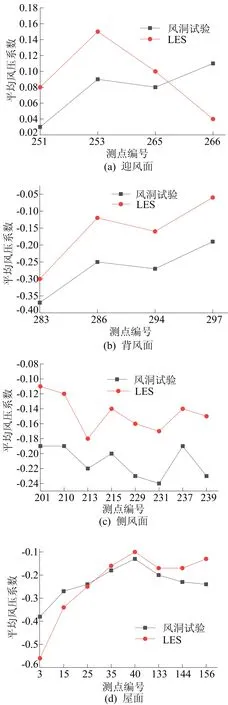
图10 平均风压系数对比

从图10可以看出,LES结果迎风面、背风面、侧风面、屋面平均风压系数分布趋势与风洞试验结果一致,迎风面风压LES结果整体上大于风洞试验结果,背风面、侧风面及屋面风压LES结果整体上小于风洞试验结果。考虑到风洞试验场地大小的限制及试验缩尺比对试验精度的影响,风洞试验仅考虑体育馆周边100 m内建筑,未考虑体育馆北侧、南侧建筑群,LES模拟考虑了体育馆周边900 m内所有建筑,来流风流经体育馆北侧建筑群发生流动分离,在建筑群后方形成涡旋,使得体育馆迎风面风压增大,背风面、侧风面、屋面的风压减小;因为气流流经体育馆南侧建筑群时,受到南侧建筑群的阻碍作用会发生回流现象,使体育馆背风面的风压进一步减小,所以背风面LES结果大小与风洞试验结果差距最大。

4.3 脉动风压系数对比

体育馆主馆迎风面、背风面、侧风面及屋面典型测点脉动风压系数LES模拟结果与风洞试验对比如图11所示。

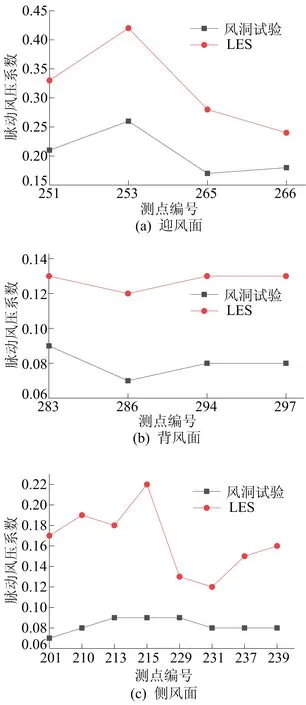
图11 脉动风压系数对比

从图11可以看出,LES结果迎风面、背风面、侧风面、屋面典型测点脉动风压系数分布趋势与风洞试验结果吻合,数值上大于风洞试验结果。流场的脉动风压受到气流的湍流强度、涡旋脱落等影响。

因为LES结果考虑了体育馆北侧建筑群,当气流流经建筑群时,气流会发生严重的流动分离,在建筑群后方形成许多涡旋,使流场气流的流动情况更加复杂,所以迎风面、侧风面、背风面、屋面的脉动风压系数均大于风洞试验结果。因为体育馆后方西侧建筑的存在,气流会发生回流现象,所以东侧风面的脉动风压大于西侧风面。

5 结 论

本文以合肥某大跨度体育馆为研究对象,采用LES方法模拟其表面风荷载,分析了0°风向角下体育馆主馆表面平均风压系数及脉动风压系数分布特征,并与风洞试验结果进行比较,得出以下结论:

(1)数值模拟得到的表面平均风压系数整体上小于规范值,但在屋盖迎风前端及屋面凸起部位,气流流动分离严重,数值模拟结果大于规范值。

(2)主馆东、西立面及顶面表面的风荷载以风吸力为主,气流在前端产生流动分离,风压梯度变化剧烈。主馆顶面凸起部位流动分离现象严重,产生极大的负风压。南立面表面风荷载也以风吸力为主,由于主馆西侧建筑的干扰,南立面平均风压系数不是对称分布,而是西侧大于东侧。主馆北立面为迎风面,以正压为主,但由于副馆的遮挡,在北立面下侧出现负压,且对称分布。

(3)主馆北、东、西立面及顶面的脉动分压分布趋势与平均风压分布相同,分布特性比平均风压复杂。南立面脉动风压分布大致对称,西侧略大于东侧。

(4)LES模型模拟结果与风洞试验相近, LES模型为研究建筑物表面的风压分布规律提供了一种低成本、简便的方法,其结果可为建筑物的抗风设计提供参考。