无人机晃动下基于相位的视觉振动检测

周 勇, 杨学志, 臧宗迪, 王金诚, 吴克伟

(1.合肥工业大学 计算机与信息学院,安徽 合肥 230601; 2.工业安全与应急技术安徽省重点实验室,安徽 合肥 230601; 3.合肥工业大学 软件学院,安徽 合肥 230601)

0 引 言

物体的振动特征能够反映该物体的某些本质属性。比如,桥梁等大型建筑的振动特征反映其结构健康状况[1-2],螺栓等连接件的振动参数反映出工厂设备的运行状态[3],人体呼吸的振动特征反映了人类的情绪和健康状况[4]。基于视觉的振动检测方法具有便捷与低成本的优势,且能够避免接触式传感器对目标振动产生的干扰,受到国内外学者的广泛关注[5]。

视觉振动检测系统利用相机捕捉目标振动视频,将三维图像信号转换为振动信号,进而获取振动频率等参数。固定相机能够完成小范围、地面位置的目标振动测量,然而对于桥梁等大型基础设施的振动检测,固定位置的视觉测量系统则难以实现。这种情况下,通常需要使用多个相机布置测点,相机的部署位置、测量视角等都需要精确计算;此外,实际环境中某些位置并不适合架设相机。

无人机技术的发展为这一问题提供了可能的解决方案,通过无人机搭载相机进行拍摄,能够克服相机部署位置的局限性。然而,无人机在飞行过程中受到气流的影响会产生随机晃动,造成所拍画面不稳定,无人机平台的视觉振动检测系统需要克服这一问题。

对于结构的振动变化,近年来有研究将欧拉视角下的相位分析法应用于振动检测。文献[6-7]将基于相位的运动分析法与欧拉视角相结合,实现了全场运动估计。图像的相位信息相对于亮度信息,对环境光照变化和图像噪声表现出更高的鲁棒性。文献[8-9]使用基于相位的振动提取方法,通过高速摄像机测量悬臂梁、金属杆以及民用基础设施的微小振动,并开展大量的实验验证了该方法的可行性;文献[10]采用基于相位的振动信号提取算法测量了金属杆等材料的模态频率;文献[11]使用基于相位的运动估计和放大方法测量了风力机叶片的谐振频率;文献[12]在基于相位的运动处理框架上实现目标的振动模态分解,并在实验室搭建的小型建筑结构上进行了验证;文献[13]对原有的相位振动检测方法进行了改进,简化了振动波形的提取过程。然而,上述研究所提出的算法只适用于稳定的相机,当应用于无人机平台时,会因气流所引发的相机晃动而失效。

对于无人机平台的振动检测,有学者使用特征点追踪的方式实现。文献[14-15]利用无人机搭载相机拍摄实验室桥梁模型,检测图像特征点并求解运动矩阵,进而测量目标的振动时程、频率等参数。这两项研究均假设图像背景区域的运动信号反映无人机晃动,并通过手动选取背景特征点提取干扰信号,完成运动校正,从而准确测量目标振动。

但是,特征点追踪的运动分析方法本质上基于亮度信号,对光照变化和图像噪声较为敏感;并且这两项研究中,背景特征点依赖于手工选取,引入了很大的工作量。文献[16]使用无人机捕捉地面人体的呼吸振动信号,首先对无人机所拍摄的视频进行稳像处理后,然后通过基于相位的运动信号提取方式完成呼吸振动检测。然而,稳像算法可能会抑制目标振动信号本身,从而影响检测结果的准确性。

本文提出一种抗无人机晃动的视觉振动检测算法。该算法基于局部相位的信号提取方式,利用晃动信号的全局性和目标振动信号的局部性对信号进行分离。首先根据像素点亮度变化剧烈程度实现目标振动区域与背景区域的分离;其次对图像的背景区域进行特征点提取,并求解背景区域的运动矩阵;然后对目标区域进行运动矫正,去除其包含的背景信号分量,即晃动信号分量;然后提取目标振动区域的局部相位序列,构建振动信号,并检测其振动频率。实验结果表明,该算法能够有效去除无人机晃动干扰,实现无人机在晃动情况下的振动检测。

1 本文算法

本文提出的无人机晃动下的视觉振动检测算法以局部相位提取振动信号为基础,以相位的运动信号提取方式处理振动信号,根据振动区域亮度变化更为剧烈这一特征,定位出振动区域;然后对图像背景区域进行特征点提取,得出背景点的运动矩阵,即无人机在气流等影响下产生的晃动信号的运动矩阵,通过这个运动矩阵对目标区域进行矫正,消除无人机晃动的影响;最后提取目标区域的局部相位序列,构建振动信号并检测目标区域的振动频率。

本文所提算法的流程框图如图1所示,包括3个主要步骤:

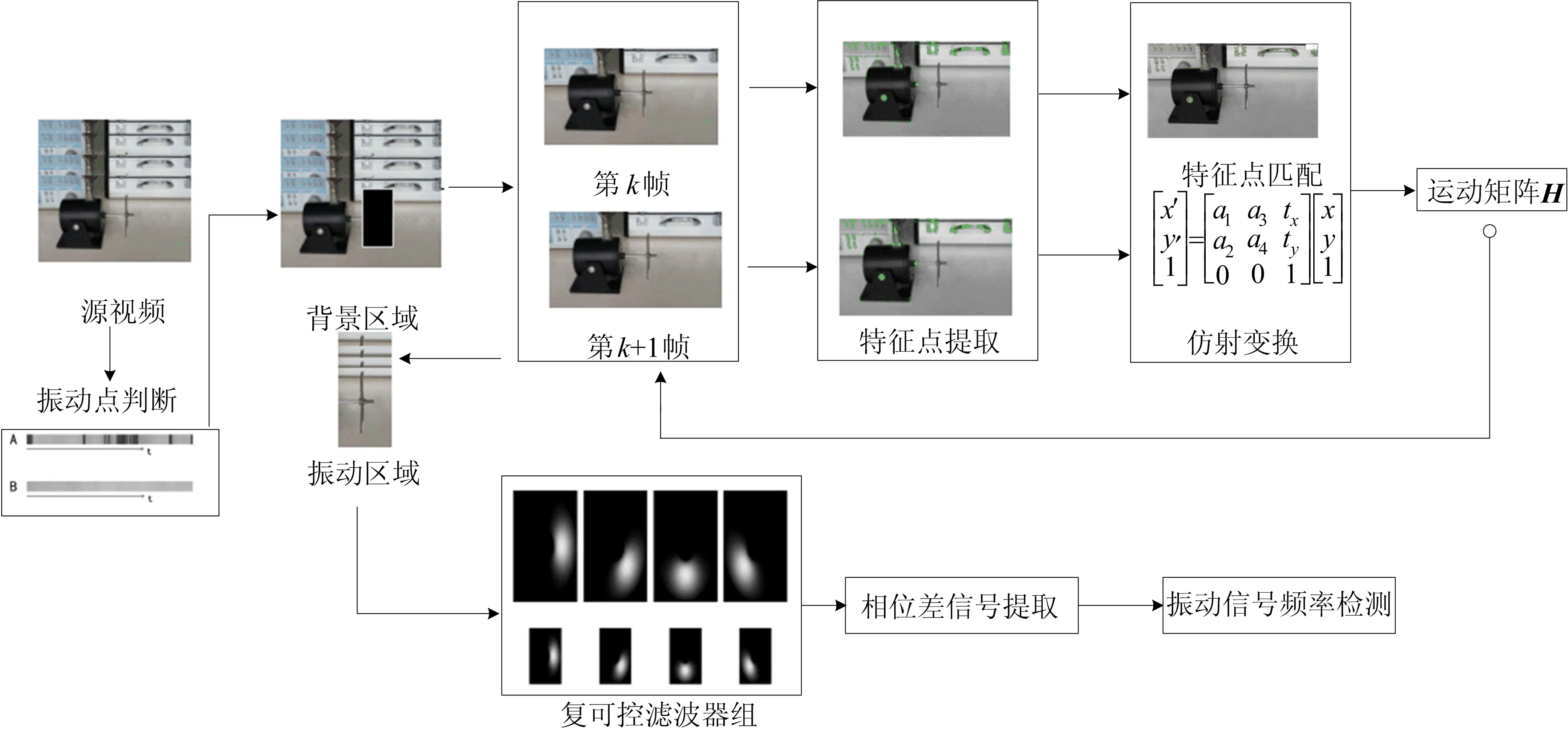
图1 本文算法流程

(1)振动目标定位与分离;

(2)无人机晃动信号矫正;

(3)基于相位的振动信号提取。

1.1 振动目标定位与分离

分离目标区域与背景区域,一方面是为了增强所提取振动信号的纯净度,另一方面是为了利用背景特征点对无人机晃动信号建模。像素点的位置变化可以与其亮度变化相对应,即图像的运动信息可以由其亮度信息来表示,因此本文根据像素点亮度变化特征识别目标点与背景点。目标像素点的运动由目标自身振动引起,而背景像素点的运动则对应无人机的晃动。本文做以下2个假设:① 无人机自身的晃动信号,相比较于振动信号,在时间域上是线性的;② 振动信号包含高阶运动分量,不具备线性变化特征。

1.1.1 二阶差分滤波

使用二阶差分滤波的方式可实现振动点与背景点的分离。I表示视频的第1帧图像;(x,y)为图像任意一点坐标；i(x,y,k)为视频第k帧图像(x,y)点所对应的亮度信号,1≤k≤N,N为视频总帧数,则滤波后信号if(x,y,k)可表示为:

if(x,y,k)=i(x,y,k+2)-

2i(x,y,k+1)+i(x,y,k)

(1)

目标点的亮度-时间序列通过该滤波器后,仍有较大的能量剩余;背景点的亮度-时间序列经过二阶差分滤波后则大幅衰减。

实验时选取的不同位置如图2所示,图2中:A点代表振动区域的点；B、C点代表非振动区域的点。A、B、C3点的亮度序列(intensity sequence,IS)及其滤波后信号的亮度序列(IS-Filtered)如图3所示。由图3a、图3b可知，A点在滤波前由振动信号与无人机晃动信号的叠加,在亮度上变化比较明显,亮度-时间序列变化比较剧烈，在经过二阶差分滤波后还存在大量的能量残余。由图3c、图3d可知，B点只有无人机晃动信号,因此B点属于平坦区域,B点的亮度-时间序列趋于一个常量,并且变化并不明显，经过二阶差分滤波之后可以看出几乎没有能量残余。由图3e、图3f可知，C点处于导线边缘,在只有无人机晃动的信号下才会有亮度变化的较大波动。

图2 振动区域与非振动区域

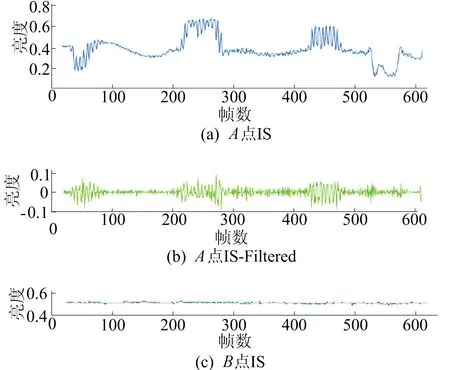
图3 3点滤波前后亮度序列

从图3e、图3f还可以看出，通过二阶差分滤波器的亮度-序列趋于0,由此可知,二阶差分滤波对于滤除线性运动,找寻有振动的区域是有效的。

1.1.2 基于能量的目标分离

在对图像进行二阶差分滤波后,用ef(x,y)表示某一位置(x,y)处滤波后亮度信号的能量大小,则有:

(2)

根据整幅图像滤波之后的能量大小,构造振动能量矩阵E:

(3)

矩阵E表示图像中每个位置所含振动信号的强弱,然后以σ为阈值实现ef(x,y)的二值化:

EBW(x,y)=f(ef(x,y))=

(4)

通过(4)式实现矩阵E的二值化EBW=f(E)。σ的选取依赖于经验,一般取σ=0.2 max(ef(x,y)。

完成以上操作后,二值图像中可能包含振动信号的点会被置1,背景点则会被置0。采用图像形态学操作,去除EBW中面积过小的连通区域,得到修饰后的振动能量矩阵EBW′。一方面由于在视频画面存在晃动时,振动目标通常会扫过一块较大的面积,另一方面为了便于后续处理,将EBW′的非零区域扩展为小矩形块,从而得到表征振动目标的模板矩阵M。将模板矩阵M与视频的每帧图像I相乘即可分离出目标振动区域与背景区域。具体如图4所示。

图4 振动目标定位

1.2 目标区域晃动信号校正

无人机晃动引发图像背景产生整体运动。对图像背景区域进行运动特征的分析则能够实现对无人机晃动信号的估计,处理过程使用角点检测算法(features from accelerated segment test,FAST)[17]与特征点提取算法(fast retina keypoint,FREAK)[18]算法实现背景区域特征点的检测和匹配,通过采样一致估计(m-estimate sample consensus,MSAC)[19]剔除误匹配点。完成全局运动模型的建立并构建得到仿射变换矩阵,然后对目标区域进行矫正。具体实现方法如下。

1.2.1 特征点提取

根据目标点与周围点的灰度差来确定特征点,FAST算法步骤如下:① 从图片中选取一个目标像素点p,设其像素值为Ip;② 设定一个合适的阈值t;③ 选取16个以目标像素点p为中心,半径为3的像素点,像素值分别记为Ij,j=1,2,…,16;④ 满足判决函数有连续的9个像素点的那个像素点即为角点。判决函数为:

S=|I-Ij|>t

(5)

1.2.2 特征描述与匹配

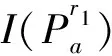
(6)

(7)

在特征描述中,得到了512 bit的二进制描述符,该描述符的列是方差由高到低的排列,高方差表征模糊信息,低方差表征细节信息。因此,选取前128 bit(即16字节)进行匹配,若2个待匹配的特征点前16字节距离小于设定的阈值,则再用剩余的比特位进行匹配。最终得到视频任意两帧图像之间的匹配点集。

1.2.3 矫正目标区域

完成背景区域的特征点检测和匹配后,使用MSAC算法[19]完成全局运动模型的建立。MSAC可以自动判断出正确的匹配点对(内点),剔除误匹配(外点),并且计算出第1幅图像的所有特征点映射到第2幅图像的运动模型。该模型由如下一个3×3的矩阵描述,即

(8)

其中:(tx,ty)为平移量;am(m=1,2,3,4)为控制图像的旋转和缩放。为了简化计算,使用以下只有1个参数的变换矩阵来代替仿射变换矩阵:

(9)

对Hi求逆,可以消除两帧图像之间背景区域的整体运动。用Gk表示第1帧图像背景区域和第k帧图像背景区域之间的映射关系,则Gk可以由上述帧与帧之间的变换矩阵Hi累积表示如下:

(10)

所求Gk描述了背景区域的运动,即实现了无人机晃动信号的估计。Gk可用来对目标振动区域进行校正,去除其包含的无人机晃动分量,保留振动分量。设Ok表示第k帧目标振动区域,(xk,yk)为其任意一点,(xk,yk)∈Ok,T表示校正变换,则有:

(11)

其中，(xk′,yk′)为校正后的点坐标。将目标区域的所有点完成校正,得到Ok′=T(Ok)。

1.3 基于相位的振动信号提取

完成对目标区域晃动信号矫正后,需要提取振动信号,提取流程如图1所示。首先在空间上,使用复数可控滤波器组对视频的每一帧进行不同尺度、不同方向的子带分解,获取到相位变化序列;然后在时域上滤除相位序列的直流分量,滤波后的相位序列即为目标振动信号;对振动信号进行傅里叶变换,检测其幅频响应函数峰值,即可得到振动频率，算法原理如下。

傅里叶变换获取到的空间全局相位与图像的整体运动相关,与之类似,空间局部相位可以用来计算局部运动。复可控金字塔(complex steerable pyramid,CSP)可以实现空间局部相位的提取。本文以一维全局傅里叶基为例说明振动与相位之间的关系，用f(x)表示位置x处的图像亮度,进行傅里叶级数展开,ω表示每个子带的空间频率，则有:

(12)

用v(t)表示振动引发的位置变化,则有：

(13)

其中每个子带可以表示为：

Sω(x,t)=Aωeiω(x+v(t))

(14)

由于每个子带都是复指数函数,相位ω(x+v(t))含有运动信息。滤除其直流分量,得到相位变化信号Vω(x,t)=ωv(t)，Vω(x,t)为位置x处的振动信号。

复可控金字塔可以将视频的每一帧亮度信号分解为不同尺度、不同方向的局部相位,这些处理后的局部相位信号可提取出视频中的目标振动。用Cλ,θ表示某一空间尺度λ、某一方向θ的复可控滤波器,则有：

A(x,y,k)eiφ(x,y,k)=Cλ,θ(x,y)⊗T(Ok(x,y))

(15)

其中:A(x,y,k)为复可控滤波得到的局部幅值;φ(x,y,k)为复可控滤波得到的局部相位。滤除φ(x,y,k)的直流分量,即可得到振动信号V(x,y,k)。经傅里叶处理后,可得峰值振动频率f为:

f=maxA(f)FFTk(V(x,y,k))

(16)

其中:A(f)为变换后得到的幅度求最大值;FFTk表示对变量k(即时间)做傅里叶变换。

2 实验结果与分析

2.1 实验设备及数据

实验系统由1台DJI Mavic Air 2无人机、1台SA-SG030扫频信号发生器和1台SA-JZ002模态激振器组成。使用信号发生器模拟真实场景中电机等设备的不同振动频率,使用无人机在不同晃动幅度下拍摄激振器视频,测量激振器顶端杆的振动频率。无人机所拍视频的分辨率为1 080 像素×1 920 像素,帧率为60 帧/s。通过手动操纵遥控杆可使无人机产生3种不同幅度(小幅、中幅、大幅)的晃动，其中小幅晃动由无人机静止拍摄产生。

使用无人机拍摄激振器振动视频,拍摄时长为10 s。计算多个特征点在不同帧的坐标间的欧式距离,选择最大距离作为无人机晃动幅度的估计。按照无人机晃动程度的不同将实验视频分为3组:组别1(晃动幅度0～30 像素)、组别2(晃动幅度30～60 像素)、组别3(晃动幅度60～90 像素)。激振器的振动频率可通过信号发生器调节,将激振器频率分别设置为5.2、10.2、15.2 Hz,每个频率点拍摄10段视频,一共采90段视频作为实验数据集。实验场景如图5所示。

图5 实验场景

2.2 评价标准

(1)平均绝对误差Me,用来反映所测频率与真实频率的绝对误差平均值，计算公式为:

(17)

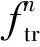
(2)均方误差RMSE,用来反映在多次测量结果中,检测频率偏离真实频率的程度,计算公式为:

(18)

2.3 实验结果

2.3.1 验证实验

本文使用对真实频率为10.2 Hz的激振器进行频率检测,从不同晃动幅度的3组视频中各选取1段视频进行处理,生成的频谱图如图6所示。

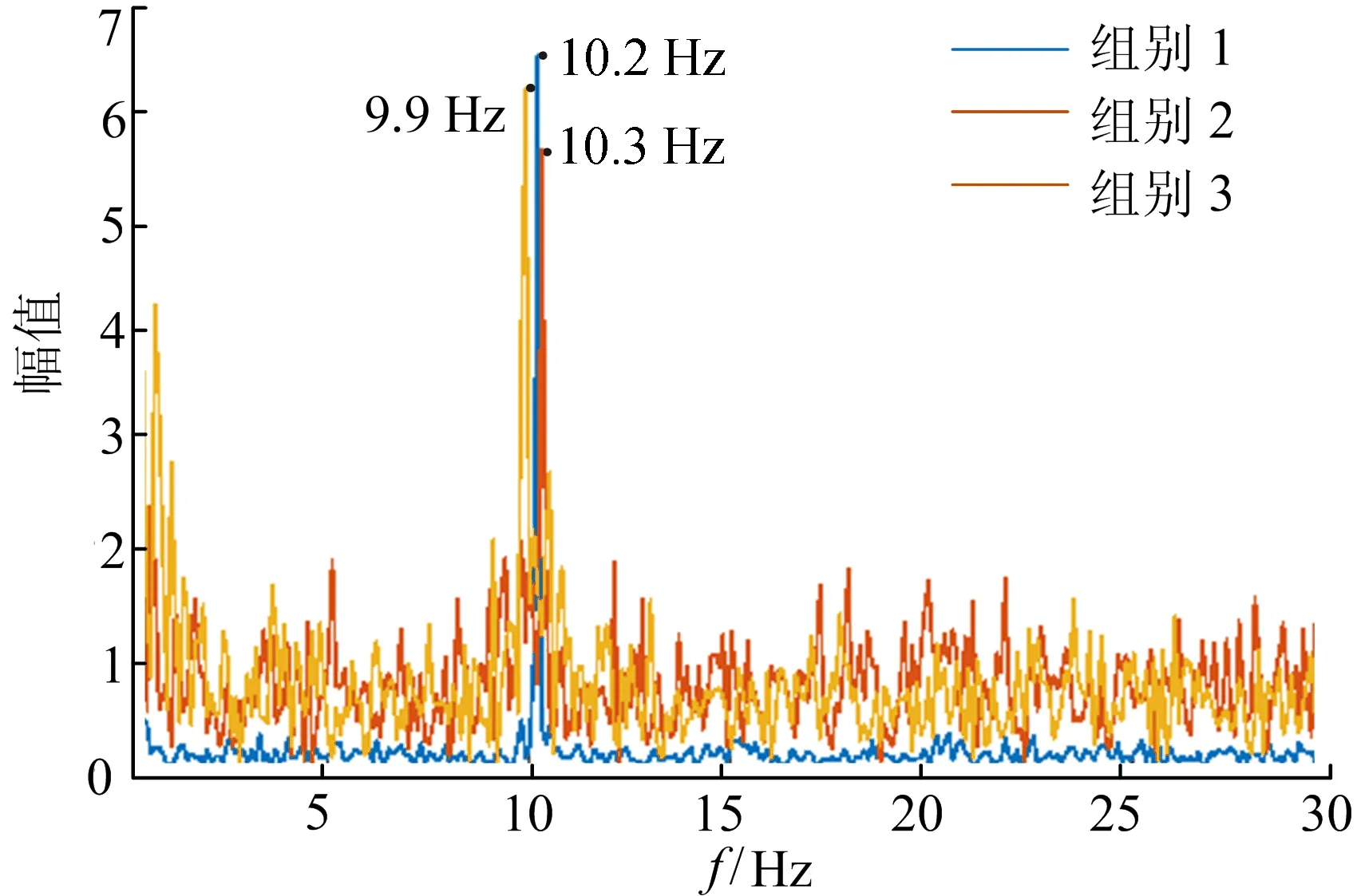
图6 不同晃动幅度检测频谱对比

从图6可以看出，组别1测得的峰值频率为10.2 Hz,组别2为10.3 Hz,组别3为9.9 Hz。结果表明,本文算法在不同晃动幅度下均能准确测得振动信号，当晃动幅度增大时,误差相应增大。为了进一步验证本文算法的检测效果,计算3种晃动幅度、3种振动频率下的平均绝对误差和均方误差,对采集的全部90段视频进行频率检测,结果见表1所列。

表1 本文算法检测结果

由表1可知本文算法的平均绝对误差控制在0.2 Hz以内,均方误差不超过0.22 Hz。

2.3.2 对比实验

将本文算法与文献[13]使用的相位检测算法、文献[15]使用的特征点追踪算法、文献[16]使用的稳像后相位提取算法进行频率检测对比。组别1中振动频率为10.2 Hz的视频在各方法下的频率检测结果如图7所示。从图7可以看出，文献[13]、文献[15]、文献[16]算法的峰值频率分别对应0.3、10.6、8.9 Hz,而本文算法检测结果为10.2 Hz。相比于本文算法,其他3种算法都存在较大误差。由该组实验可以看出,本文算法能够有效去除无人机晃动干扰,准确提取出视频中的振动信号,相比于其他算法的检测结果，本文算法的误差更小。为了进一步对比上述算法的检测效果,对采集的全部90段视频进行频率检测,检测结果见表2～表4所列。

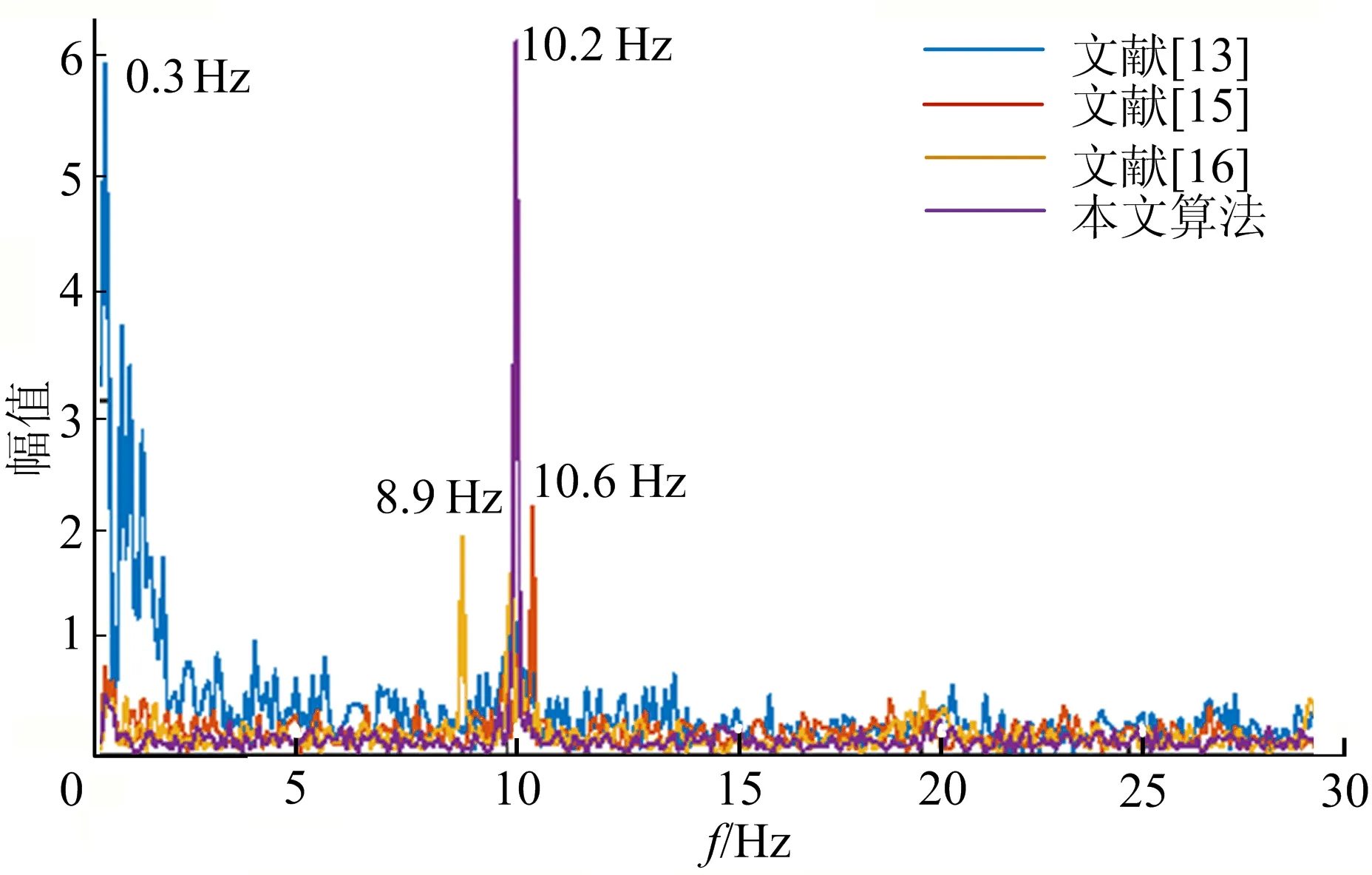
图7 10.2 Hz下不同算法频率检测对比

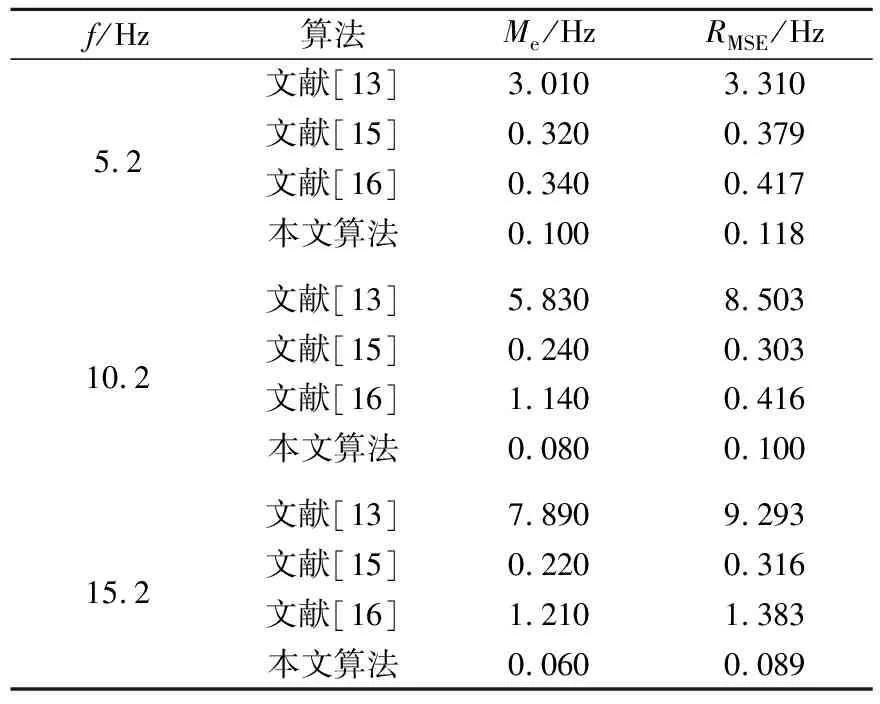
表2 0～30像素晃动下检测结果

表3 30～60 像素晃动下检测结果

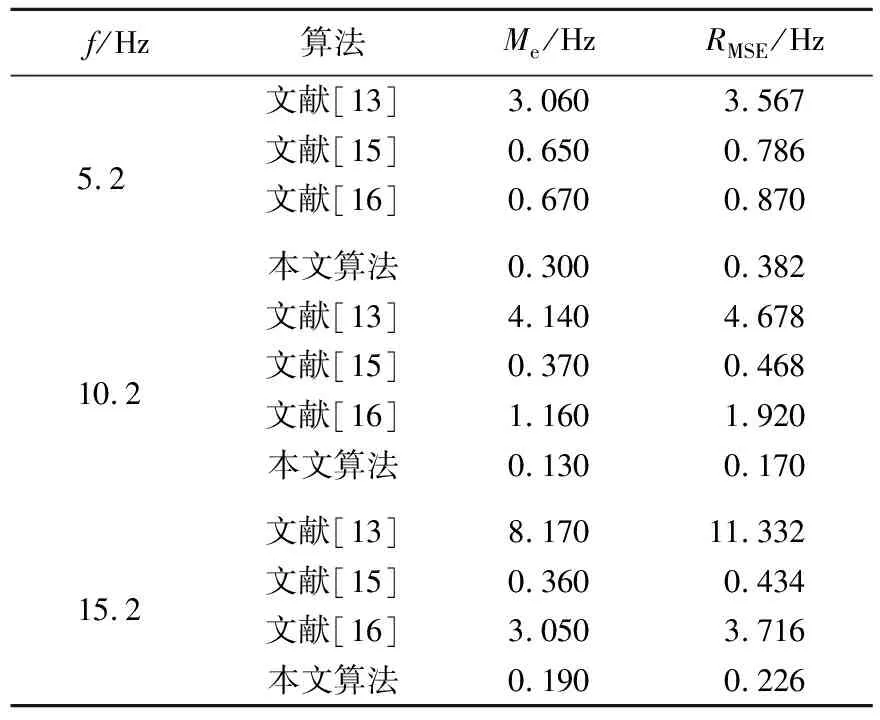
表4 60～90像素晃动下检测结果

从表2～表4可以看出,对比文献[13]、文献[15]、文献[16]算法,分别在5.2、10.2、15.2 Hz下对应3个不同幅度无人机晃动的检测结果,发现本文算法均优于另外3种算法。

2.3.3 实验分析

本实验对本文算法与文献[13]、文献[15]、文献[16]3种算法进行准确性分析,结果见表5所列。

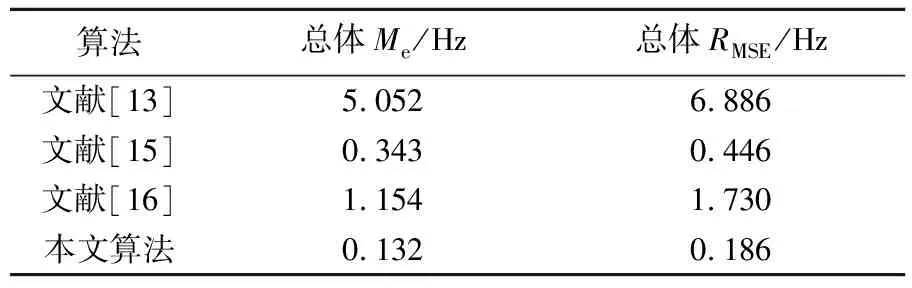
表5 准确性分析

从表5可以看出,本文算法取得了最佳的检测效果,分组平均绝对误差和均方误差均保持在0.2 Hz的范围内,总体平均绝对误差为0.132;文献[15]算法检测性能次之,总体平均绝对误差0.343;文献[16]算法整体检测性能欠佳,总体平均绝对误差超过了1;而文献[13]算法整体误差过大,超过了可接受的范围,因此可判定该算法对于无人机晃动下的振动检测失效。

原因在于：文献[13]不加区分地将全场运动信号转化为相位信息,未处理相机晃动,引入了大量低频干扰,导致目标振动信号被湮没;文献[15]算法通过手动选定背景特征点实现运动矫正,保留了振动信号,但由于其采用基于亮度特征的振动提取方式,因而其振动检测准确性上低于本文的相位检测法；文献[16]算法虽然针对无人机引发的相机晃动进行了稳像处理,但是由于其未区分目标振动信号和晃动信号,从而导致振动信号产生了畸变。

本文算法实现了振动和背景区域的分离,以背景区域的特征点完成对无人机运动矩阵的求解,从而去除振动区域的晃动干扰,准确提取出了目标振动视频中的待测振动信号。

在不同晃动幅度下将本文算法与其他3种算法的平均绝对误差进行对比,见表6所列。从表6可以看出:对于文献[15]、文献[16]以及本文算法,随着无人机晃动幅度的增大,3种算法的频率检测误差均明显增大；文献[15]采用特征点追踪框架,当晃动增大时,其特征点匹配错误的可能性增加,造成性能下降；文献[16]使用稳像算法对视频进行处理后,再进行基于相位的振动检测，由于视频稳像依赖特征点匹配,因而晃动幅度增加会影响其稳像预处理的性能,进而降低频率检测准确率。

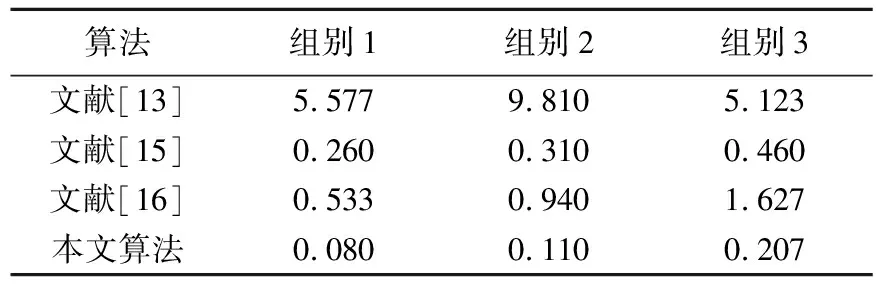
表6 3种晃动幅度下平均绝对误差分析 单位:Hz

对于本文算法,由于无人机运动矩阵的求解同样依赖特征点匹配,检测准确率必然随着晃动幅度的增大而降低。

在不同频率下将本文算法与其他3种算法的平均绝对误差进行对比，结果见表7所列。

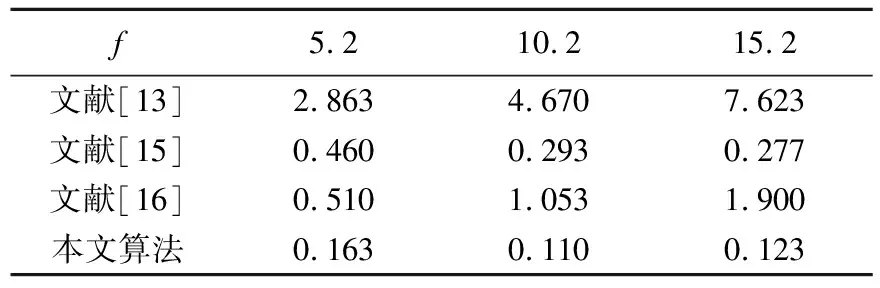
表7 不同振动频率下平均绝对误差分析 单位:Hz

由表7可知，由于文献[13]算法在实验场景下已基本失效,因此不做进一步分析；文献[15]算法和本文算法在不同振动频率下的检测性能无明显差别；而文献[16]算法则在测量高频信号时,准确率明显降低。原因在于：文献[16]算法基于视频的全局稳像,稳像过程会去除剧烈变化信号,保留图像序列的平滑运动，如果目标的振动频率较高,那么算法可能会对目标本身的振动产生抑制效果,进而影响频率检测的准确性；文献[15]算法通过人工选择背景特征点实现晃动信号的估计；本文算法则在自动分离背景区域和振动区域的基础上,使用背景区域的特征点求解无人机运动矩阵。因此这2种算法均不会对目标本身的振动产生影响。

2.3.4 算法时间复杂度分析

将本文算法时间复杂度与文献[13]、文献[15]、文献[16]算法时间复杂度进行对比分析,结果见表8所列,视频每帧分辨率为1 080像素×1 920 像素,每个视频总共为600帧,使用5个不同的视频进行实验。

从表8可以看出，本文算法的时间复杂度优于文献[13]、文献[16],但比文献[15]更耗时。这是由于文献[13]使用的是全局相位检测算法,由于对视频每帧整体进行计算,本文算法在矫正分离后只对振动区域进行相位检测算法,只计算每一帧部分位置，因而本文算法耗时更少。

表8 不同算法时间性能分析 单位：s

对比文献[15]采用特征点追踪算法,在算法的时间复杂度上比本文算法更优。文献[16]采用全局稳像再使用相位检测算法,首先稳像是针对全局进行,而本文算法的矫正只针对目标区域,在这一阶段本文的算法就会耗时更少。而且文献[16]在使用稳像算法之后再进行全局的相位检测算法,整体来看，本文算法的时间复杂度明显优于文献[16]。

3 结 论

本文提出了一种抗无人机晃动的视觉振动检测算法,该算法利用目标物体的振动特征,从视频中分离出振动目标和背景区域,利用背景区域计算出无人机在气流扰动下晃动的运动矩阵,利用得到的运动矩阵实现对目标区域里叠加的无人机晃动信号进行矫正,得到较为纯净的振动信号,然后通过复可控滤波器提取振动信号的相位序列,检测其振动频率。

在真实使用场景中,振动目标不一定总能够保持在拍摄画面内,当无人机晃动幅度过大时,目标可能会短暂的丢失在视频帧中,这会影响到本文算法的准确性。

在未来的工作中,将针对更大幅度的无人机晃动以及更为复杂的无人机测量场景开展研究,以拓宽本文算法的应用范围。