基于机器学习模型的汽车定位的自动优化

夏文艺

福特汽车工程研究南京有限公司，江苏南京 211100

0 引言

为了满足整车尺寸技术规范(dimensional technical specification,DTS)的要求，减少尺寸链的影响，汽车零件的定位设计必须满足对关键测量点敏感度不能大于一定规范值，即装配时来自基准的偏差而导致零件测点的偏差被放大的系数不能超过规范要求。基于VSA或者3DCS两款分析软件都能实现定位敏感度的计算，但都没有优化功能，若结果不满足要求，需要人为反复调整尝试，而且无法确定最优解的位置。

本文利用开源框架PyTorch搭建机器学习模型，通过反向计算梯度，实现GD&T基准较于测点的敏感度的梯度下降，完成GD&T基准的自动优化。

1 自动优化模型的搭建

定位敏感度的计算通过模拟将零件3-2-1对齐虚拟工装,之后分别在虚拟工装基准赋单位偏差计算测点处的变化量即敏感度。以敏感度误差结果作为损失函数反向计算定位基准的梯度，以创建优化模型。

1.1 定位敏感度的计算

虚拟工装上基准的坐标值分别赋单位偏差，以下虚拟工装的坐标值和零件的坐标值将分别记为实际值和目标值。对齐原理为3-2-1，那么实际值和目标值分别为对应形状6×3的矩阵。3-2-1对齐得到的旋转正交矩阵为R，偏移矩阵为B。测点为M，测点方向为V。敏感度S的计算公式为：

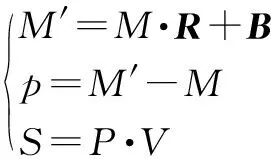
(1)

图1为VSA计算的敏感度与模型所计算敏感度的差值对照，表明模型计算结果一致。

图1 VSA计算的敏感度与模型所计算敏感度的差值对照

1.2 过程能力模拟

假设实际基准偏差为±0.5，则实际基准的分布均值为0，3σ为0.5的正态分布。1 000次采样对齐之后某一测点的分布如图2所示[1],与VSA-DVA结果一致。

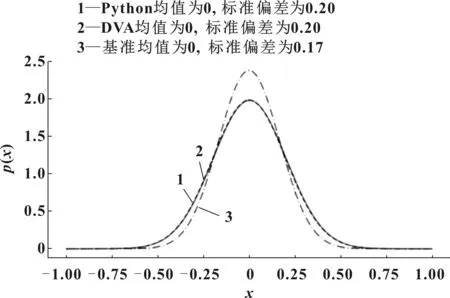
图2 某一测点的分布

1.3 定义损失函数和优化器

损失函数L为：

L=S2/2

(2)

反向梯度的计算公式依据链式法则：

(3)

优化器的更新原理依据泰勒的一阶展开式，φ为学习率。

(4)

由于PyTorch支持自动微分和生成计算图，所以微分方程不需要手动计算。

2 模型的对比分析

2.1 实际零件的定位数据和测点位置数据

参照汽车的尾灯零件定位，其定位数据见表1。

表1 零件的定位数据

零件的测点位置数据见表2。

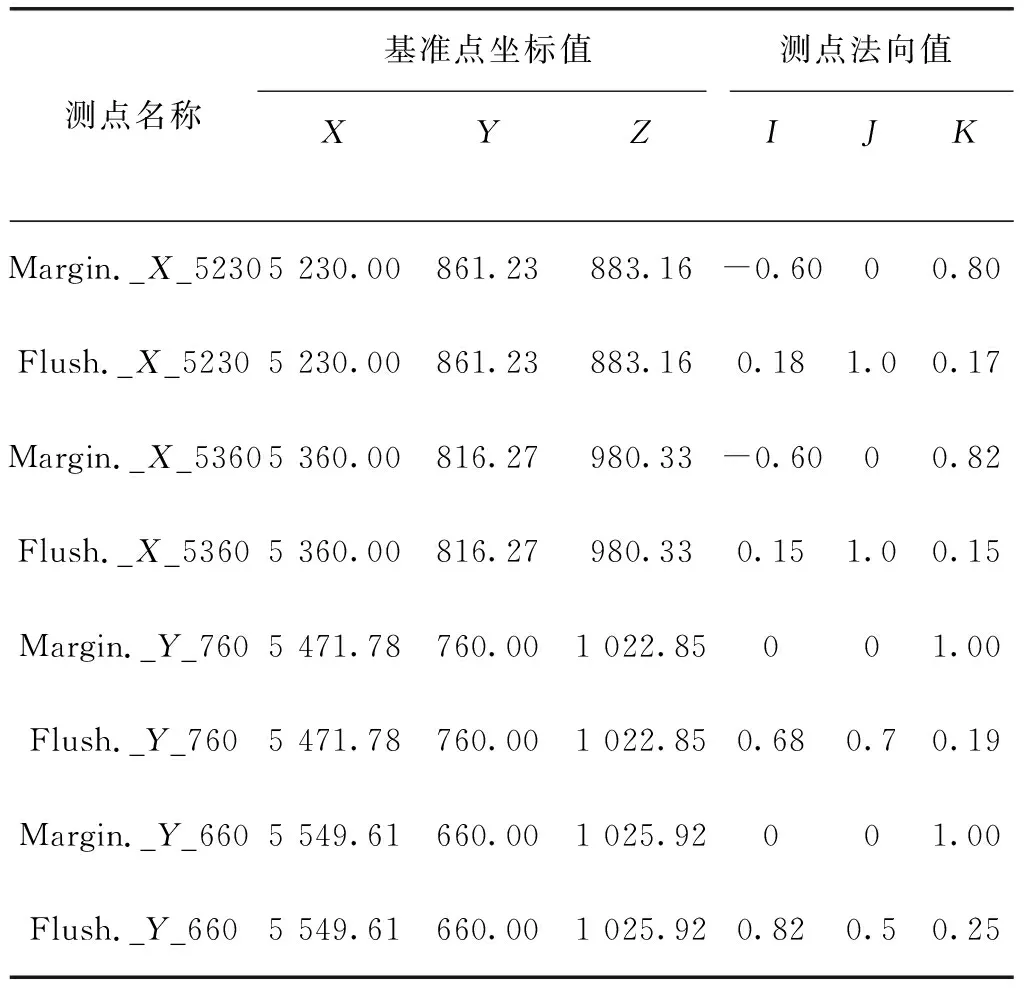
表2 零件的测点位置数据

2.2 局部定位的自动优化

图3为模型计算出的基准敏感度。

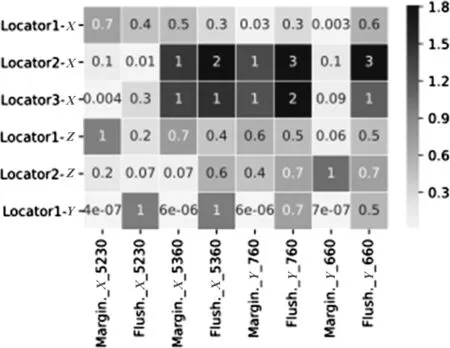
图3 模型计算出的基准敏感度

由图3可以看出 ，定位名为Locator2-X的偏差有几处测点放大达到3倍，已经不能很好地保证零件的稳定性。

首先利用模型单独对Locator2-X定位点进行自动优化，可以看到随着每个迭代周期，Locator2-X的坐标值全部进行更新，更新过程中损失值在不断下降[2]，迭代过程如图4所示。

图4 迭代过程

图5为自动优化后定位的敏感度，即更新完成500次迭代以后新坐标下基准的敏感度。

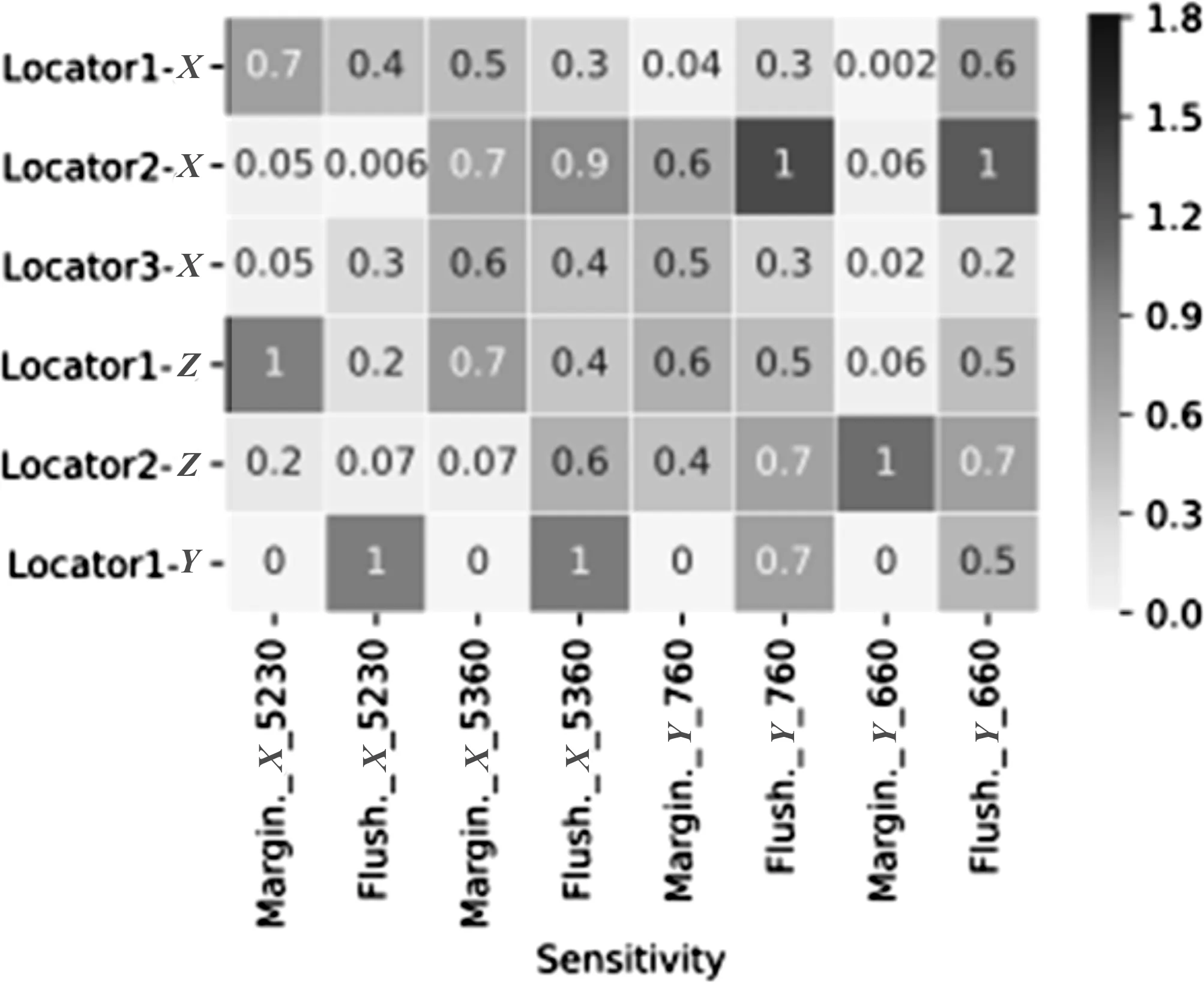
图5 自动优化后定位的敏感度

由图5可以看出，自动优化后敏感度降低明显，利用CATIA等作图软件可以绘制基准的优化轨迹。Locator2-X优化轨迹3D显示如图6所示。由图可以看出，随着迭代次数的增加定位位置不断得到优化。

图6 Locator2-X优化轨迹3D显示

2.3 全局优化及在范围内寻找最优解

根据零件的尺寸范围及边缘为迭代增加边界检查函数，超出边界即选取边界值。同时对所有定位进行迭代优化，这里迭代800个周期。图7为所有基准同时优化收敛曲线。由图可以看出，损失值不断下降，同时所有基准的坐标不断更新。

图7 所有基准同时优化收敛曲线

由于增加了边界检查函数，所以损失值收敛的曲线会出现急剧变化的部分[3]。增加了轮廓周围的更多测点，计算优化后的定位敏感度。优化前轮廓测点敏感度如图8所示，优化后轮廓测点敏感度如图9所示，通过对比图8和图9，发现全局定位敏感度降低明显。

图8 优化前轮廓测点敏感度

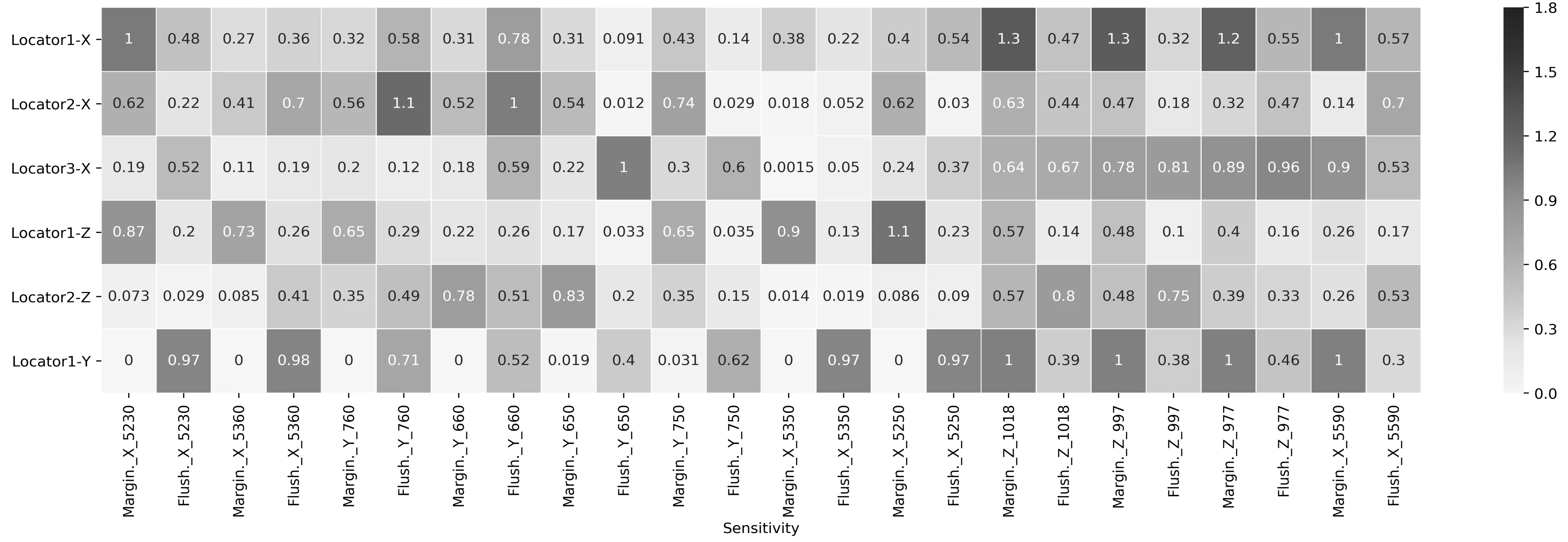
图9 优化后轮廓测点敏感度

利用CATIA绘制3D显示优化前后基准位置的变化，如图10所示。

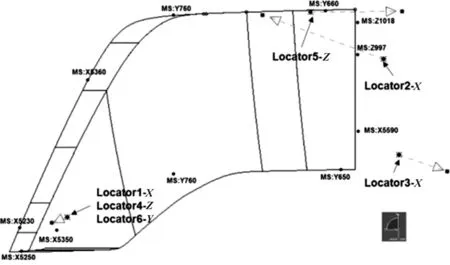
图10 全局定位优化3D显示

由图10可以看出，模型在优化过程中每个定位点都会自动在梯度方向进行优化，超出边界范围后会在允许的范围继续寻找最优解，实现自动优化功能。

3 结论

利用机器学习可以实现车身零件定位系统的自动优化，给定敏感度目标得到最优解，同时加入边界限制元素，在一定区域内寻找定位优化的理想状态。

综上可见，机器学习可以在解决尺寸链问题时，基于测点的位置及要求，提供自动优化定位设计方案，避免盲目反复手动试错来调整。