有限时间收敛的引信滚转角控制方法

张雨薇，李 冰，祁克玉，2

(1.西安机电信息技术研究所,陕西 西安 710065；2.机电动态控制重点实验室，陕西 西安 710065)

0 引言

新的战场环境要求下，武器弹药高速发展，不断升级，炮弹的精确打击能力，毁伤效率越来越受到重视[1]。二维弹道修正组件不仅提高了传统“笨弹”的射击精度，同时未对原本弹体外形和发射装置进行额外改动，可消耗原有库存，效费比良好。目前国内的二维弹道修正引信多采用精准制导组件(PGK，precision guided kit)方案。

PGK方案采用轴承连接二维弹道修正引信头部与弹体，修正弹飞行过程中差动安装的导转翼面使头部与弹体发生相对旋转运动；弹上根据实时预测落点给出修正翼面静止的目标角度，电机根据控制算法提供控制力矩使引信相对地面静止，控制同向安装的修正翼面停在期望滚转角，产生不同方向的修正力和力矩[2]。

文献[2]提出了一种基于模糊控制的滚转角控制方法；但是该方法对系统模型的精确度依赖较高，工程应用性较差。文献[3]基于传统PID控制提出了采用双闭环的滚转角控制算法，可以做到在1 s内完成滚转角的控制，误差均值为3°左右；但是真实外弹道环境比较复杂，算法在实际使用上存在困难。文献[4]通过偏差信号对PID参数自整定，研究了基于PID控制的专家系统控制算法，大大提高了响应速度；但是滚转角响应时超调量太大，不利于滚转角控制系统的稳定和可靠性。

本文针对滚转角控制系统响应要求的快速性和准确性，基于滑模控制的理论选取合适的趋近律，设计一种有限时间收敛的滚转角控制方法。

1 滚转角运动数学模型及有限收敛概念

1.1 滚转角数学模型

对于二维弹道修正引信的PGK方案来说，轴承连接修正引信和弹体。发射后，弹体从弹尾看高速右旋，启控前修正翼面在导转力矩的作用下右旋；启控后，翼面在电机控制力矩的作用下相对地面静止在期望的滚转角。整个飞行过程中，二维弹道修正引信会受滚转力矩、轴承摩擦力矩，滚转阻尼力矩等的影响[5]。

因此，二维弹道修正引信滚转角的数学微分方程组[5]如下所示：

(1)

式(1)中，Jx为引信部分极转动惯量，ωx为引信部分滚转角速率，γx为引信滚转角，Me为电机的控制力矩，Mf为连接处的轴承摩擦力矩，MFx为导转翼面产生的导转力矩，MFxz为引信滚转阻尼力矩。

1.2 有限时间收敛定义

针对滚转角控制系统设计一定时间内收敛的控制算法时，首要明确对于非线性系统有限时间稳定[6]的相关定义。

定义 考虑系统如下：

(2)

式(2)中，定义f(x,t)满足f:U0×R→Rn于U0×R段连续，U0这里定义为原点的一个开邻域。

如果系统在x=0(局部)时满足有限时间收敛，是指考虑任意选取的t0当作初始状态，都一定能找到一个依赖于x0的停息时间T≥0，让系统拥有一个有定义的以x0为初始状态的解x(t0)=φ(t:t0,x0)(不一定是唯一解)，并且

(3)

在此情况下当t∈[t0,T(x0)]时，满足φ(t:t0，x0)∈U/{0}。

同时，对于系统的平衡点x=0(局部)满足有限时间稳定，指的是它首先是满足李雅普诺夫稳定的，同时在原点的一个邻域U∈U0里是满足有限时间收敛的[7]。若同时邻域满足U=Rn，那么原点就是满足全局有限时间稳定的平衡点[6]。同时存在如下引理。

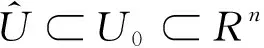
系统停息时间的大小取决于初始值x(0)=x0，其上界为

(4)

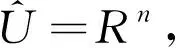
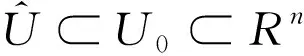
引理3 如果存在一个系统同时满足全局渐进稳定和局部有限时间收敛，那么这个系统是满足全局有限时间稳定的[7]。

2 有限时间收敛的滚转角控制算法

对于采用PGK方案的滚转角控制系统来说，控制的核心是对落点预测给出的期望滚转角进行迅速响应并且翼面滚转角速度尽快为0，保持翼面与地面的相对静止，因此对整个滚转角控制系统的可靠性和快速性提出要求。

目前工程应用中考虑可靠性多采用PID经典控制算法，但是传统PID参数固定，对建模精确性要求高，不能很好适应变化情况不固定的滚转角指令，同时抗干扰能力较差。因此目前多采用专家系统、模糊控制等算法进行优化[8]。

基于滑模变结构的理论和有限时间收敛的定义，设计一种二维弹道修正引信的滚转角控制算法，同时结合引理对设计的有限时间收敛的滚转角控制方法进行证明。

2.1 变结构算法

假设期望的翼面滚转角为γf，设置状态变量为x=ωx,期望设计的算法同时满足对滚转角的精确控制和滚转角速度的快速响应，因此考虑构造如下的方程当作滑模面：

S=c1|γ-γf|c2sgn(γ-γf)+x，

(5)

式(5)中，00，对式(5)进行求导后，可得

(6)

(7)

联立式(6)和式(7)得

(8)

由滚转角的微分方程组可以得到

(9)

因此，将式(9)代入式(8)，经过整理可得，PGK方案所需要的电机控制力矩大小为

(10)

对式(10)在进行仿真的时候，还可以进行适当的变换与化简，r=r1-V(t-t1)。为了降低抖动，可以将符号函数sgn换成S/|S|+δ的形式来平滑，δ取一个很小的正数。

2.2 有限时间收敛分析

需要从趋近滑模面的运动和沿着滑模面的运动两个方面来证明所设计的滚转角控制算法满足有限时间内收敛的定义。

首先证明所设计的控制算法能够在一定时间内到达所设计的滑模面。

选取李雅普诺夫函数V=S2，进行求导后，可以得到

(11)

从李雅普诺夫函数的相关定理，可以判断所设计的滚转角控制系统是符合渐进稳定的相关定义，也就是有限收敛的。通过整理设计的李雅普诺夫函数可得

(12)

根据上述条件，可得对于下降段的任意t>0时，

(13)

通过引理1可以得到，所设计的滚转角控制系统是可以在有限时间内到达所设计的滑模面，考虑具体的时间上界

(14)

接下来证明当二维弹道修正引信的滚转角控制系统到达滑模面以后，沿着滑模面的运动阶段是否能满足有限时间收敛。因为此时滚转角控制系统已经位于S面上，因此有

S=c1|γ-γf|c2sgn(γ-γf)+x=0。

(15)

代入滚转角系统微分方程，整理可得

(γ-γf)′=-c1|γ-γf|c2sgn(γ-γf)。

(16)

对式(16)，选取Lyapunov函数V1=(γ-γf)2。

对函数求导后有

(17)

可以得到

V1=-2c1V′0.5(c2+1)≤0。

(18)

所设计的二维弹道修正引信的滚转角控制系统满足引理1的条件，因此系统是渐进稳定的。即当t→∞的时候，这个系统的状态变量x→0，即二维弹道修正引信部分的滚转角速率收敛为0，修正引信的滚转角会无限接近于所设置的期望滚转角。

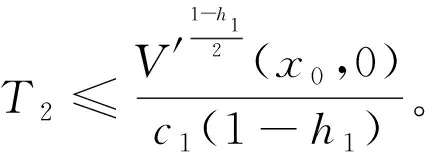
通过对两个方面的证明推理，根据引理3可知，设计的有限时间收敛的滑模滚转角控制方法是全局有限时间稳定的。最后收敛总共用时T≤T1+T2(估计)。

通过对算法的有限时间稳定性分析表明，所设计的滚转角控制算法能够在有限时间内保证滚转角速率快速收敛到0，并收敛到期望的滚转角，系统具有一定的鲁棒性。

3 仿真验证

对所提出的滚转角控制方法进行仿真验证。仿真时考虑摩擦力矩估计误差、滚转角测量误差、滚转角速度测量误差等误差源，如表1所示。

表1 滚转角控制算法仿真误差源Tab.1 Simulation error resources of roll angle control system

假设引信滚转角初始位置为0°，设计引信目标滚转信号分别为90°，180°，仿真步长0.001 s，分别用传统PID滚转角控制和所设计的滚转角控制算法进行仿真，仿真结果如图1—图4所示。

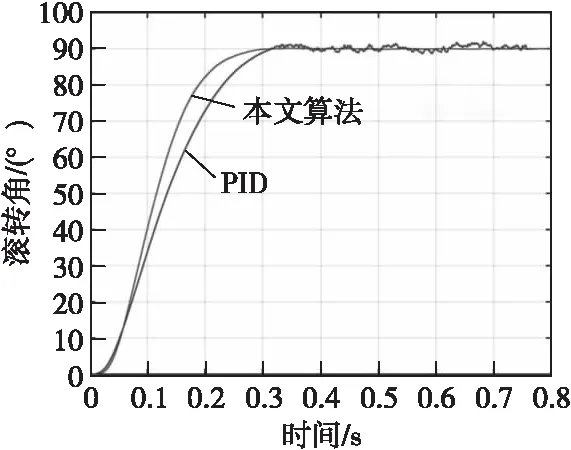
图1 2种算法90°滚转角控制效果对比图Fig.1 two algorithmic control effect with Step response of 90°roll angle

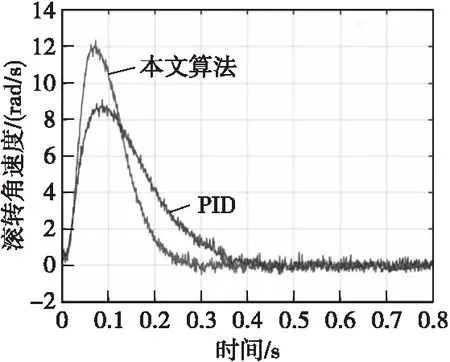
图2 2种算法90°滚转角速度对比图Fig.2 two algorithmic control effect with Step response of 90°roll angle velocity

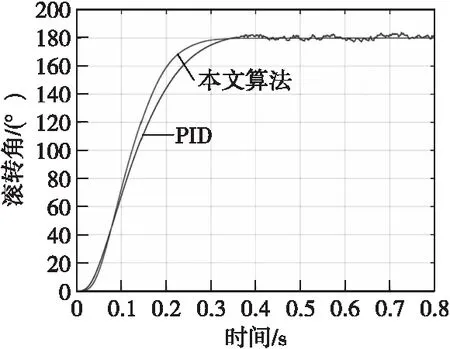
图3 2种算法180°滚转角控制效果对比图Fig.3 two algorithmic control effect with Step response of 180°roll angle

图4 2种算法180°滚转角速度对比图Fig.4 two algorithmic control effect with Step response of 180°roll angle velocity

由图1—图4可知，单纯采用PID控制的方案滚转角误差均值为4.21°，误差均方差为0.94°；采用本文所设计的控制律进行仿真后，滚转角误差均值为0.68°，误差均方差为0.43°，控制精度明显提高。引信的滚转角速度能够0.3 s内迅速静止且制动到目标位置，满足估计时间上界，与不进行参数优化的PID方法比较，在对滚转角的响应速度、控制精度以及对建模精准度的要求上都具有优势。

因此，本文设计的二维弹道修正引信的滚转角控制系统对干扰具有强鲁棒性，且响应更迅速，控制精度更高。

4 结论

本文针对滚转角控制系统响应要求的快速性和准确性，基于滑模变结构的理论，利用系统有限时间收敛的概念，设计了一种用于二维弹道修正引信的有限时间收敛滚转角控制算法，对传统PID控制系统进行了优化。仿真验证表明，所设计的滚转角控制系统能够在短时间内定位滚转角，提高控制精度，并且系统具有一定的鲁棒性。