多跳频信号参数估计时频分析算法

张 玮，王 平

(1. 海军工程大学，湖北 武汉 430000；2. 解放军92038部队，山东 青岛 266041)

0 引言

跳频[1-2](frequency hopping, FH)通信是常用的扩频通信方式之一，信号载波频率随时间进行伪随机跳变，具有较高的抗截获、抗干扰、抗多径能力，在军事领域有广泛应用。在通信对抗过程中，获取准确的跳频信号参数是实施有效的通信干扰的前提，但是在复杂电磁环境下，获取准确的跳频参数也变得十分困难，因此跳频信号参数估计也成为了通信对抗领域的一个热点问题。

目前用于跳频信号参数估计的方法主要有时频分析法[3]和非时频分析法[4]，而时频分析法是当前主要的跳频信号分析方法。时频分析法是通过时间和频率两个维度来描述能量密度变化的方法。文献[5]提出一种基于同步压缩变换的跳频信号参数估计方法，通过提取时频脊线对跳变时刻和跳变频率进行估计；文献[6]提出一种基于时频脊线的参数估计算法的改进算法，在存在较强干扰的情况下仍能进行正确的参数估计；文献[7] 提出一种基于时频能量对消的定频干扰消除算法，并通过最小二乘法完成参数估计；文献[8]通过采取时频图谱修正和二次估计的方法获得更精确的参数估计值。但是上述算法均无法分选多跳频信号，只能完成对单跳频信号的参数估计。文献[9]提出一种改进能量对消的信号检测算法，但是存在抗噪声性能较差的问题；文献[10]提出一种基于内曼-皮尔森检验的快速调频信号检测算法，但是该算法仅能在背景噪声中进行信号检测，在含有其他干扰信号时算法无法正常运行；文献[11]提出一种基于平滑伪魏格纳分布的时域参数估计方法，具有稳定性和实时性好的特点，并且精度较高，但是存在交叉干扰的问题。

为解决上述问题，本文提出一种多跳频信号参数估计时频分析算法。通过短时傅里叶变换得到时频图像，利用能量对消、自适应阈值法和形态学滤波进行跳频信号提取，消除各类噪声影响。通过区域联通标记算法标记各个跳频簇，利用跳频簇时长对跳频信号进行分选，改进PAM聚类算法，完成调频频率和跳频周期的估计。

1 多跳频信号模型

跳频信号的频率可随时间伪随机跳变[12]，在观测时间T内共发送L个跳频信号，第l个跳频信号的数学模型可进行如下定义：

(1)

接收端接收的信号r(t)中，除了L个跳频信号外还包括复杂的干扰信号J(t)，干扰信号中存在定频信号、扫频信号、高斯白噪声、部分频带干扰等，采集到的信号可表示为

(2)

2 多跳频信号参数估计算法

本文算法具体步骤如下：

1)采用短时傅里叶变换对信号进行图像化处理，得到时频矩阵；

2)采用能量对消的方法消除定频信号干扰；

3)通过自适应阈值法处理时频图像，得到二值化图像；

4)采用形态学滤波的方法去除各类干扰信号，获得高清晰度的时频图像，完成跳频信号提取；

5)对时频图像进行区域联通标记，通过各跳频簇时长对多跳频信号进行分选；

6)通过聚类算法，完成跳频信号跳频周期和频率集的估计。

2.1 时频变换

时频变换采用短时傅里叶变换(STFT)[13]的方式，即

(3)

式(3)中，r(t)表示要处理的信号，h(t)表示窗函数，h*(t)表示窗函数的共轭函数。

为方便计算，通常可以将信号离散化处理：

(4)

图1为对接收信号进行短时傅里叶变换后的图像。

2.2 跳频信号提取

2.2.1能量对消

能量对消的方法可以有效去除定频信号干扰[7]，而当定频信号与跳频信号发生频率碰撞时，应先进行能量对消再进行二值化处理，这样可以在去除定频干扰的同时有效保留跳频信号。

对时频矩阵图像F(n,k)各频率分量求均值:

(5)

将时频矩阵图像与频率分量均值相减，可以得到对消图像：

(6)

在接收信号时间段内，定频信号强度不变并始终存在，其时频能量特征随时间变化不大；跳频信号的频率随时间进行跳变，每一频率在观测时间内存在时间非常短，其对应频率上的均值远小于跳频信号的能量值，因此采用能量对消的方法可以有效去除定频干扰保留跳频信号。

2.2.2二值化处理

为获得清晰的时频图像，可采用阈值法对图像进行二值化处理。对大于阈值的像素点赋值为1，对小于等于阈值的像素点赋值为0，便可以获得二值化图像。

(7)

常见的阈值法二值化处理主要可分为全局阈值法和局部阈值法[14]，全局阈值法是根据完整图像求取阈值，从而实现二值化处理的方法，但是当跳频信号受到部分频带干扰时，全局阈值法的效能会有部分降低，此时应采用局部自适应阈值法，示意图如图2所示。

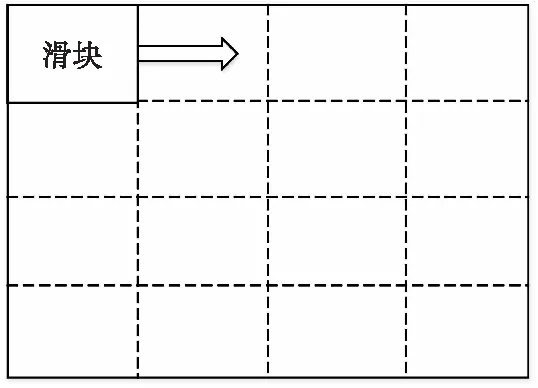
图2 局部自适应阈值法示意图Fig.2 Schematic diagram of local adaptive threshold method

本文的局部自适应阈值法，首先根据时频图像尺寸设置一个大小为m×n的移动滑块，在滑块范围内采用otsu阈值算法，计算滑块范围内的阈值，通过移动滑块遍历整个时频图像，进而求取完整的阈值，根据阈值对时频图像进行二值化处理，得到二值化图像。

2.2.3形态学滤波

通过形态学滤波，可以有效去除扫频信号、突发信号以及未清除干净的噪声点等干扰信号，也可以修复裂缝、填补空洞，达到平滑图像的效果。形态学滤波的运算主要包括开运算、闭运算以及构成开闭运算的腐蚀运算和膨胀运算，通过设定结构元素消除噪声和填补空洞[15]。开运算定义为

F2=F1(n,k)·s=(F1(n,k)⊕s)⊙s)。

(8)

闭运算定义为

F2=F1(n,k)·s=(F1(n,k)⊙s)⊕s)，

(9)

其中，·表示开运算，·表示闭运算，⊙表示膨胀运算，⊕表示腐蚀运算，s表示结构元素。

在运算过程中结构元素起到重要作用，需要保留的图形要大于结构元素，需要消除的图像要小于结构元素。因此本阶段算法首先构造矩形结构元素，采用闭运算完成弥合裂缝、填充空洞、平滑图像，然后构造线型结构元素，采用开运算消除扫频和突发信号的干扰，完成形态学滤波，并完成跳频信号提取，提取后的时频图像如图3所示。

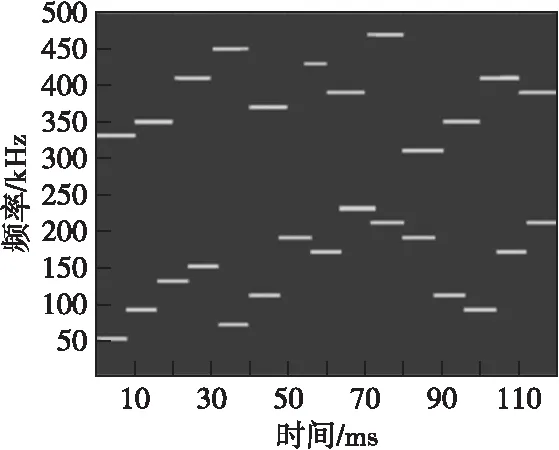
图3 跳频提取后的时频图像Fig.3 Time-frequency image after frequency hopping extraction

2.3 跳频信号参数估计

经过跳频信号提取后的时频图像中，已经消除了大部分噪声及干扰，只存在跳频信号。本文采用改进的PAM算法[16]对多跳频信号进行分选，并估计各跳频信号的跳频周期和跳频频率。

2.3.1多跳频信号分选

对提取后的跳频矩阵采用八联通标记法[17]，对跳频信号每一信号簇进行标记编号，将各跳频簇的幅值标记为编号数字，时频图像会由不同颜色表示。标记后的图像如图4所示。

图4 区域标记时频图像Fig.4 Time-frequency image of area marking

跳频信号簇H(i)以编号为索引，计算每一簇的跳频信号的长度Li，通过信号长度进行分选。

Li=max(xH(i))-min(xH(i))。

(10)

设定长度阈值，在已知只有2个跳频信号时，阈值可定为平均值，在跳频信号数量多于2个时，可以通过长度统计直方图进行多次筛选。将筛选的结果编号记录进不同的数组，以编号为索引进行后面的参数估计。以2个跳频信号为例，分选流程如图5所示：

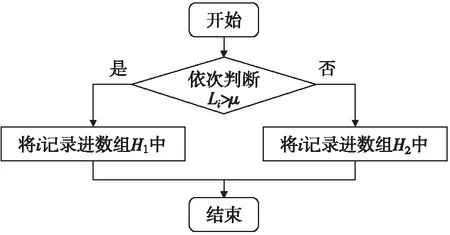
图5 信号分选流程图Fig.5 Flow chart of signal sorting

通过信号分选过程，可以将多跳频信号分为两类，以跳频簇编号为索引，通过表1的分选结果，分别对各跳频信号实施参数估计。

表1 信号分选结果Tab.1 Estimation results of real signal parameters

2.3.2改进的PAM算法

PAM算法[16]是K-means聚类算法的改进算法，随机从数据中选择K个聚类中心，聚类中心是数据对象，通过计算其余数据对象与聚类中心的距离将数据对象归于相应的簇内，再通过迭代运算得到正确的划分，并得到聚类中心。

本文算法通过区域联通标记完成各数据点的聚类，以各跳频簇为聚类计算聚类中心，减少迭代次数，有效减少复杂度。

算法描述：

1) 对单跳频簇内选取一点为初始聚类中心；

2) 计算其余各点与聚类中心欧氏距离之和，保存至数组S中；

3) 重复步骤1)和步骤2)，直至遍历跳频簇内所有数据点，设定S值最小的点为聚类中心，记录其坐标[t(i),f(i)]；

4) 遍历各跳频簇，重复步骤1)—3)，输出各聚类中心的频率坐标f={f1,f2,f3,f4，…，fn}为跳频频率估计值。输出各聚类中心时间坐标t={t1,t2,t3,t4，…，tn}，计算其一阶差分方程，求取尾切平均数，其结果作为调频周期估计值，则改进的PAM算法完成，同时完成跳频信号参数估计。

以运算次数作为算法时间复杂度对比改进的PAM算法和PAM算法，如表2所示。

表2中，N为采样点数，k为跳频簇数。改进的PAM算法的运算次数明显小于PAM算法，可见改进算法复杂度有较大的降低。

表2 算法复杂度对比Tab.2 Algorithm complexity comparison

3 仿真实验

为分析算法的抗噪声性能，对测量误差进行如下规定：

(11)

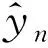
以下实验中的曲线均是在各个信噪比下100次蒙特卡洛实验结果的平均。

1) 实验一

分析在高斯噪声背景下本文算法与文献[6]和文献[8]算法的性能对比。由于文献[6]和文献[8]算法为单跳频信号参数估计算法，因此实验设置为单跳频信号的参数估计。设置采样率为1 000 kHz，跳频信号频率集为[330、350、410、450、370、430、390、470、310、350、410、390] kHz，跳频周期为10 ms，信号长度为120 000点，仿真时长120 ms。

3种算法对跳频周期和调频频率的估计误差曲线如图6和图7所示。由图可知，本文算法具有更高的估计精度，相较于对比算法有数量级上的优势，具体数据对比如表3所示。

图6 跳频周期的估计误差Fig.6 Estimation error of FH period

图7 跳频频率的估计误差Fig.7 Estimation error of FH frequency

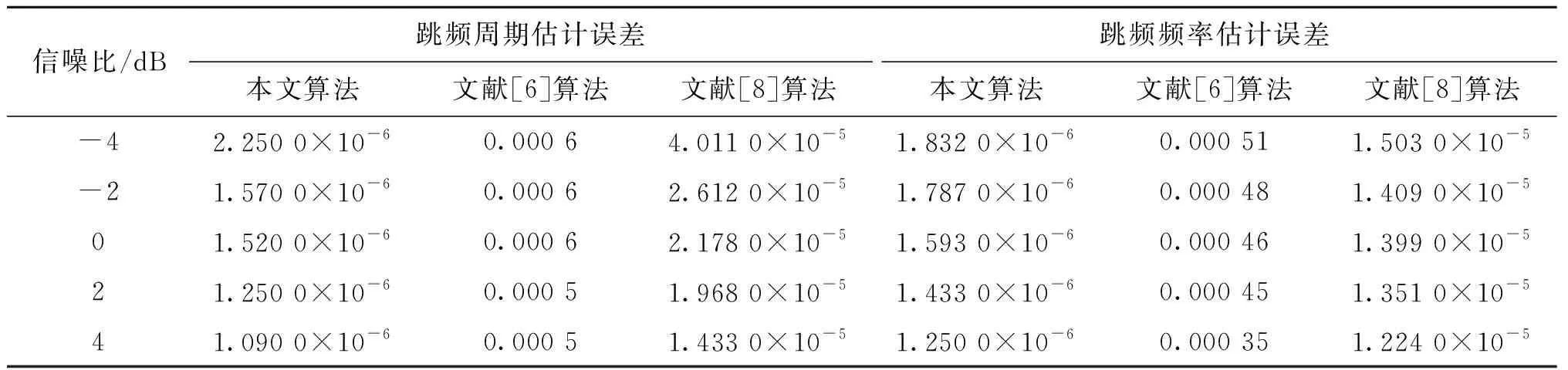
表3 参数估计误差对比Tab.3 Comparison of parameter estimation errors

2) 实验二

验证算法在不同强度和干扰下本文算法与文献[18]对多跳频信号的参数估计性能对比。设置采样率为1 000 kHz，跳频信号1频率集为[330、350、410、450、370、430、390、470、310、350、410、390] kHz，跳频周期为10 ms， 跳频信号2频率集为[50、90、130、150、70、110、190、170、230、210、190、110、90、170、210] kHz，跳频周期为8 ms，信号长度为120 000点，仿真时长120 ms。干扰信号包括3个定频信号，频率分别为150、250、350 kHz，1个扫频信号，扫频范围为260～300 kHz，扫频周期为17 ms，1个部分频带干扰，干扰频带为425～475 kHz，背景噪声为高斯白噪声。其中150、350 kHz定频干扰信号与跳频信号的两个频点发生频率碰撞。通过改变各干扰信号功率之和，在不同干信比条件下，验证算法的参数估计精度。跳频周期估计精度如图8所示，数据对比如表4所示，跳频频率估计精度如图9所示，数据对比如表5所示。

仿真结果表明，本文算法优于对比算法，估计误差总体比对比算法低一个数量级，同时，干扰越强估计精度越低，并且随着信噪比的增加，估计误差也在减小。但是在干信比从1～3 dB时，误差的数量级不变，因此可以判断各类干扰对本文算法影响较小。

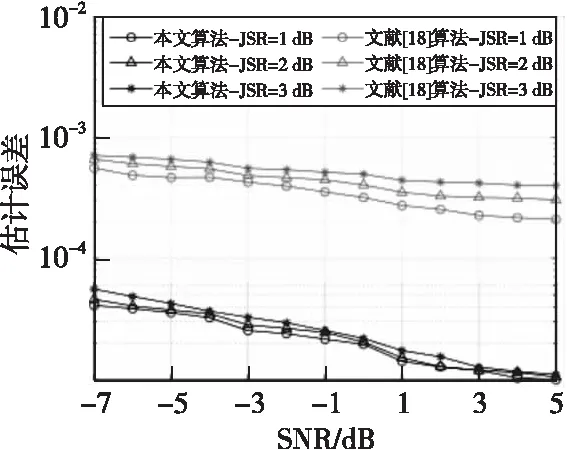
图8 不同干扰强度下的跳频周期估计误差Fig.8 Estimation error of frequency hopping period under different interference intensity

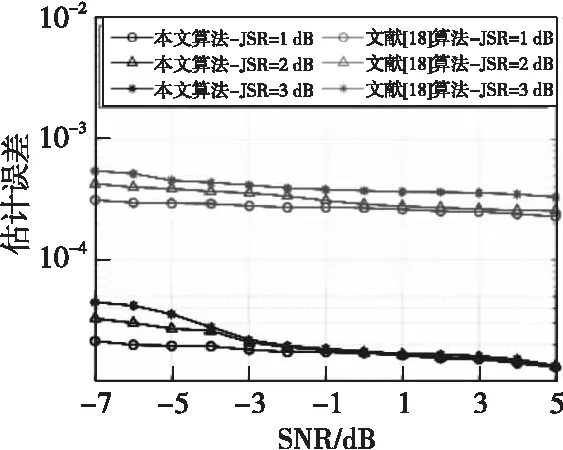
图9 不同干扰强度下的跳频频率估计误差Fig.9 Estimation error of frequency hopping frequency under different interference intensity

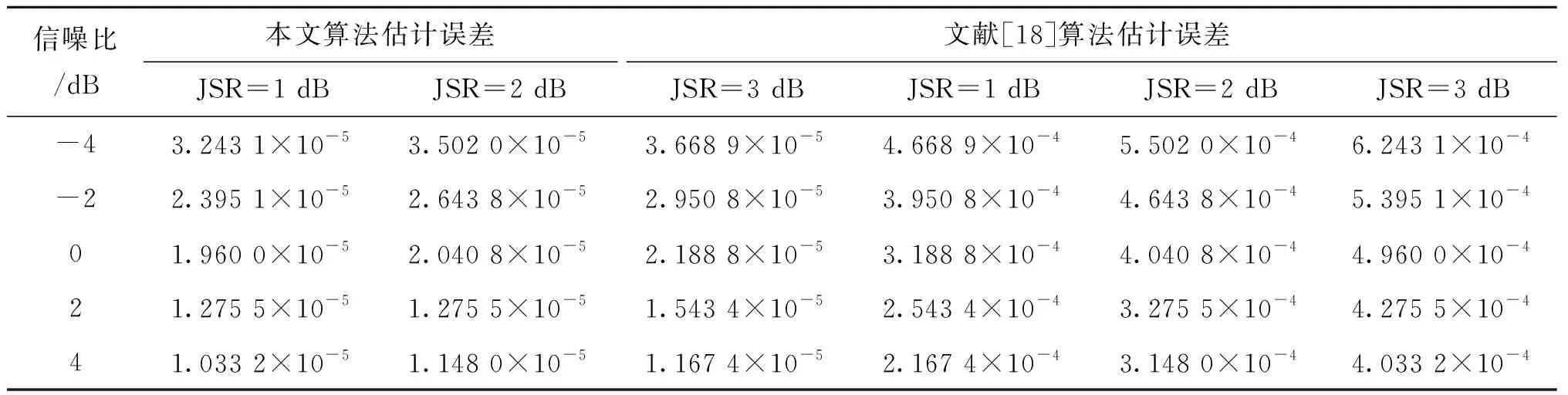
表4 跳频周期估计误差对比Tab.4 Comparison of frequency hopping period estimation error

表5 跳频频率估计误差对比Tab.5 Comparison of frequency hopping frequency estimation error

4 结论

本文提出一种多跳频信号参数估计时频分析算法，对算法的性能和影响算法精度的因素进行了仿真实验。通过对信号时频变换得到时频图像，通过能量对消、自适应阈值化处理、形态学滤波去除噪声影响，提取跳频信号；通过区域联通标记算法对各跳频簇进行标记，并通过时长对信号实施分选，改进PAM算法，完成跳频周期和跳频频率估计。仿真实验结果表明，与通过提取时频脊线的方式进行参数估计的算法相比，该算法具有更高的估计精度，同时能够准确分选出多跳频信号，在各类干扰影响下，仍具有较高的估计精度。