基于高斯伪谱法的枪榴弹制导算法

许一蒙，霍鹏飞,2，王 超，雷泷杰

(1.西安机电信息技术研究所，陕西 西安 710065；2.机电动态控制重点实验室，陕西 西安 710065)

0 引言

近年来，随着局部地区的冲突加剧，维稳和反恐行动的需求不断增加，采用低成本弹药对地面人员精确打击的需求日益增长。枪榴弹尺寸小、重量轻、成本低，特别适用于低成本精确打击人员目标[1]；但传统枪榴弹无制导，精度低，无法满足精确打击的使用需求，因此推动了枪榴弹智能化的发展。通过制导提高枪榴弹的命中精度是枪榴弹智能化设计中的重要环节。

文献[2]采用极大值原理求解弹道修正引信弹道控制中以能量消耗最小为目标的弹道控制优化模型，得到最优法向过载值；但控制优化模型的求解时间比较长，难以直接应用到枪榴弹制导中。文献[3]通过综合协同制导控制和高斯伪谱法弹道规划，实现多弹以最优路径攻击目标；但需要实时测量目标的角度偏差和弹目距离，成本过高。文献[4]以射程最大为指标，利用高斯伪谱法实现弹道的合理优化，并比较了标准位置跟踪和标准过载跟踪两种实现方法；但由比例导引得到制导指令所需过载较大，枪榴弹难以满足。文献[5]将标准弹道的某点作为目标点进行轨道计算及最优入轨控制，无需进行虚拟目标点的修正；但对制导方程进行了简化，带来了不小的误差，需要对精度进一步优化。因此，有必要结合枪榴弹的自身和任务特性，研究一种能够满足枪榴弹打击精度，且消耗能量小，解算速度快的制导算法。本文针对上述问题，提出基于高斯伪谱法的枪榴弹制导算法。

1 高斯伪谱法

高斯伪谱法无需对微分方程求解，收敛半径大，收敛速率快且精度较高，适用于需要快速解算的枪榴弹弹道。

高斯伪谱法的本质就是同时离散控制变量和状态变量的直接法，也被称作配点法或直接配点非线性规划DCNLP(direct collocation with nonlinear programming)。高斯伪谱法的解算步骤：首先在一系列的LG(Legendre-Gauss)点上将状态变量和控制变量进行离散；然后通过离散点为节点，采用全局多项式插值，对控制变量和状态变量进行近似逼近，从而将系统从微分约束转化为代数约束；最后以节点处的状态变量和控制变量作为优化变量，将最优控制问题转化为非线性规划问题而求解。

弹道优化问题是复杂的多约束动态优化问题，可将其看作一般的最优控制问题，一般最优控制问题的Bolza形式描述如下：

minJ=Φ[x(t0),t0,x(tf),tf]+

(1)

式(1)中，u(t)∈Rm为控制变量，x(t)∈Rn为状态变量，t0和tf为时间的初始值和终端值。

系统满足的动力学约束、边界条件约束和路径约束分别为

(2)

求解优化问题应对优化问题参数化，具体流程如下。

1)一般非线性系统的动力学方程

由式(2)可知，非线性系统的动力学方程的一般形式为

(3)

2)时域变换

由于最优控制问题的时间变量t∈[t0,tf]，而高斯伪谱法的时间变量τ∈[-1,1]，因此，将t离散到τ：

(4)

3)近似状态变量与控制变量

高斯伪谱法的离散点个数为K+1个，其中包括K个LG点和τ0=-1点，从而构成K+1个Lagrange插值多项式Li(τ)(i=0,1，…,k)，以此为基函数，进行状态变量的近似：

(5)

其中，

(6)

(7)

其中，

(8)

以上问题中对于状态变量是在[-1，1)的时间区间内近似的，未对终端状态τf=1进行定义，终端状态满足动力学方程约束：

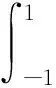
(9)

对终端状态约束条件进行离散并以高斯积分来近似，得到

(10)

4)动力学方程约束转为代数约束

对式(5)求导可得状态变量的导数，将动力学方程约束转换为代数约束：

(11)

从而可得状态变量在节点处需满足的代数方程约束：

(12)

5)近似性能指标函数

将Bolza形式的性能指标函数中的积分项用高斯积分近似，可得到用于高斯伪谱法中的近似性能指标函数：

(13)

经过上述步骤，高斯伪谱法将连续最优控制问题转换为一般非线性规划问题[6-8]。

2 基于高斯伪谱法的枪榴弹制导算法

2.1 制导策略

基于高斯伪谱法的枪榴弹制导算法的基本策略：采用指令制导方式，发射前一次性规划，发射后持续修正。发射前，根据目标位置，采用高斯伪谱法规划出一条需用能量最小的最优标准弹道。制导过程中，在发射点处实时测量并解算出实际弹道相对于发射点的高低角qy和方位角qz与标准弹道的高低角偏差Δqy和方位角偏差Δqz，形成制导指令，导引弹丸飞向目标。制导策略的示意图如图1所示。

图1 基于高斯伪谱法的枪榴弹制导策略Fig.1 Guidance strategy of grenade based on Gaussian pseudo-spectral method

2.2 弹道模型建立

本文采用三自由度(3D)质点弹道模型，将枪榴弹视为理想质点，不考虑弹体绕质心转动的影响，假定攻角为零，空气动力只计阻力。建立描述枪榴弹质心运动的方程组如下：

(14)

2.3 优化模型建立

由于能量的大小和过载大小正相关，由式(14)可以看出，过载矢量大小的主要影响因素是速度V、弹道倾角θ和弹道偏角ψv，因此建立优化问题如下[10-12]：

1)性能指标：本文以枪榴弹所需修正能量最小为指标，可得

(15)

2)状态约束：为式(14)运动方程组。

3)边界条件：满足以下边界条件

(16)

4)过载约束：由于枪榴弹所能提供的修正过载有限，因此对其进行约束：

(17)

优化问题求解流程如图2所示。

图2 弹道优化流程Fig.2 Trajectory optimization process

2.4 制导指令计算

定义模拟产生发射点处实时测量和解算的高低角和方位角的偏差为

(18)

式(18)中，qyt、qzt为实时弹道高低角和方位角；qyc、qzc为标准弹道高低角和方位角。

根据测量得到的高低角和方位角偏差计算制导指令：

(19)

式(19)中，K1,K2为比例系数。

3 仿真验证

本文以40 mm枪榴弹为例，使用Matlab/Simulink软件进行弹道优化和制导仿真。

3.1 弹道优化仿真

假设枪榴弹发射点坐标(0，0，0)m，目标点坐标(2 000，2，0)m，发射初速v0=230 m/s，修正过载区间(-0.5,0.5)，以所需修正能量最小为指标，选取插值点数为30，利用Matlab中GPOPS-ii工具箱进行基于高斯伪谱法的弹道优化，优化后的弹道如图3所示。

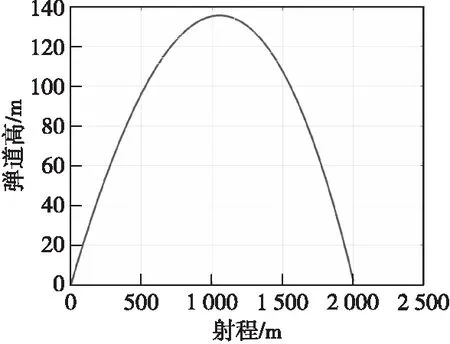
图3 优化后的标准弹道Fig.3 Optimized standard trajectory

同时，可以得到最优弹道的初始射角为13.724 8°，初始偏角为0°。

3.2 制导仿真

3.2.1理想情况仿真

不考虑射击诸元误差、气象误差、角度测量误差等，以3.1节中经过高斯伪谱法优化的最优弹道为标准弹道，采用2.4节中制导指令的计算方法，以初速度v0=230 m/s，目标点坐标(2 000，2，0)m，初始射角14°，初始偏角0.5°为初始条件，以射程x=2 000 m为停止条件进行制导仿真，以实际弹道和标准弹道进行对比，仿真结果如图4所示。

图4 实际弹道与标准弹道对比Fig.4 Comparison between actual trajectory and standard trajectory

仿真末端位置数据如表1所示。

表1 制导仿真末端数据Tab.1 Terminal data of guidance simulation

以上理想情况下制导仿真数据表明，末端弹道高y，横向偏移z方向误差小于0.1 m，末端高低角qy,方位角qz角度误差小于0.01 rad，该制导方法实现了对优化后标准弹道的跟踪。

3.2.2真实情况仿真

考虑到枪榴弹射程小、弹道低，忽略气象对弹道的影响，针对初速误差和角度测量误差分析制导精度。取名义初速度v0=230 m/s，初速散布误差均方差取1‰v0，初始射角均值13.7°，方差1°，初始偏角均值0°，方差1°，目标点坐标(2 000，2，0)m，考虑诸多误差因素，随机生成100组数据进行打靶仿真试验，仿真结果如图5所示。

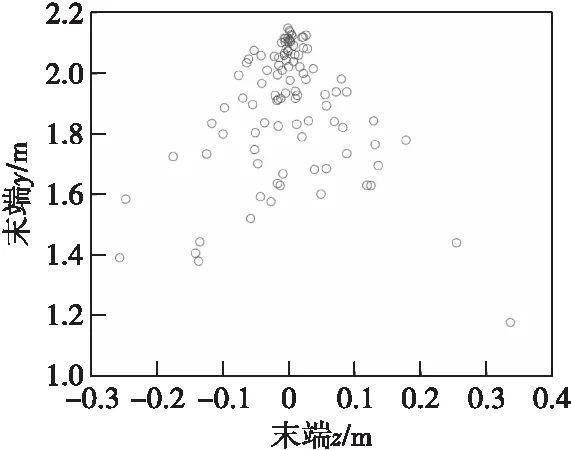
图5 100组打靶仿真试验结果Fig.5 100 groups of shooting simulation tests

为评估该制导方法的精度，用以上100组打靶仿真试验数据进行RCEP(圆概率误差)计算，公式如下：

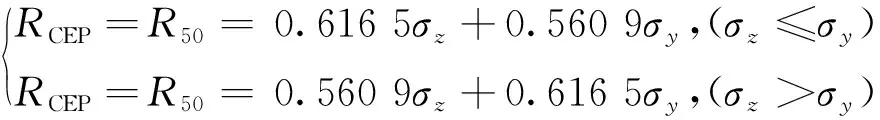
(20)

式(20)中，σ为末端位置均方差。

代入以上生成的100组打靶仿真试验数据，解得该制导方法的RCEP=0.17 m。

3.3 与其他制导方法对比

本文以最小修正能量为性能指标，依据由高斯伪谱法优化后的最优弹道为标准弹道进行制导，仿真对比该制导方法、传统比例导引法和落点预测制导法的修正结果，仿真中初速度v0=230 m/s，目标点坐标(2 000，2，0)m，初始射角14°,初始偏角0.5°，枪榴弹重0.5 kg，图6为三种制导方法过载对比。

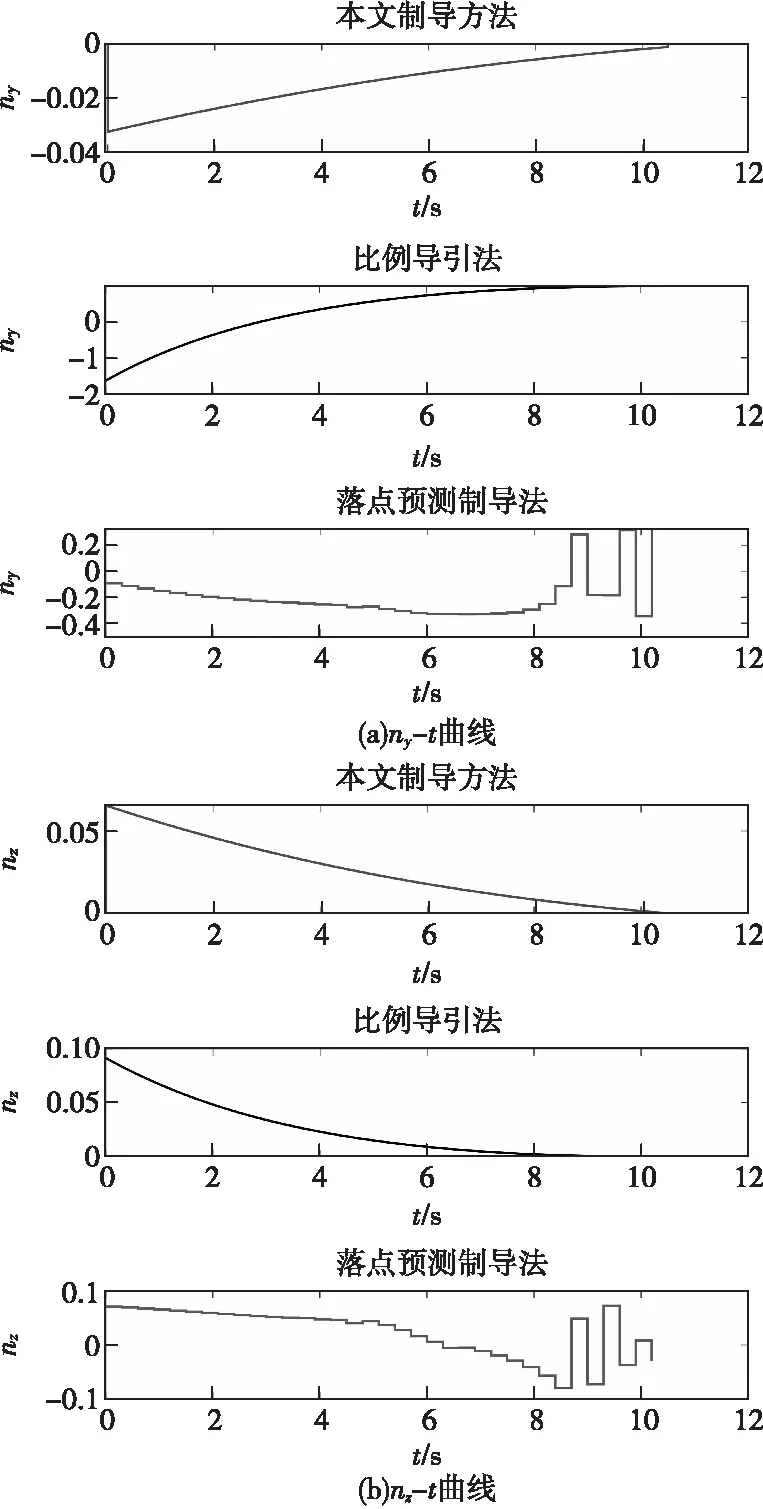
图6 基于高斯伪谱法的制导制算法、比例导引法与落点预测制导法的修正过载对比Fig.6 Comparison of modified overload between guidance algorithm based on Gaussian pseudo-spectrum method, proportional guidance method and impact prediction guidance method

由图6可知，比例导引法所需修正过载较大，约为本文制导算法的50倍；落点预测制导法虽然修正过载较小，但末端过载出现了明显震荡，不利于末端的修正；本文所述制导方法修正过载小且末端无震荡，具有明显优势。

依据修正过载计算上述三种制导方法所需的修正能量，再对其余两种制导方法进行同3.2.2节所示的100组打靶仿真试验，计算RCEP，结果见表2。

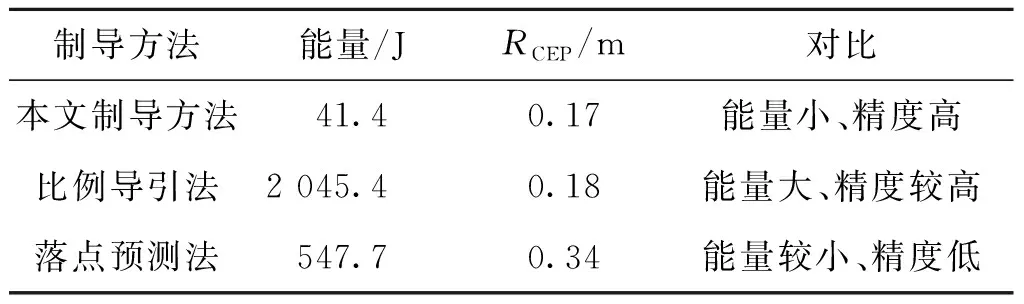
表2 三种制导方法对比Tab.2 Comparison of three guidance methods

由表2可以看出，本文制导方法所需的能量约为比例导引法的2%，约为落点预测制导法的8%；本文制导方法的RCEP约为落点预测制导法的50%，与比例导引法RCEP大致相同，但从能量角度考虑，比例导引法所需能量更大，对于尺寸小、成本低的枪榴弹要提供比例导引法所需能量的难度更大，成本过高。综上所述，本文所述制导方法的修正能量明显小于比例导引法和落点预测制导法的修正能量，且RCEP优于比例导引法和落点预测制导法。

4 结论

本文提出基于高斯伪谱法的枪榴弹制导算法，该算法以最小修正能量为性能指标，利用高斯伪谱法优化出一条最优弹道作为标准弹道，依据实时弹道和标准弹道的偏差生成制导指令。以40 mm枪榴弹为例，与比例导引法和落点预测制导法进行制导性能对比，仿真结果表明，本文制导方法所需修正能量最小，仅为比例导引法的2%，是落点预测制导法的8%；本文制导方法的RCEP小，约为比例导引法的94%，约为落点预测制导法的50%。因此基于高斯伪谱法的枪榴弹制导算法具有修正能量小，制导精度高的特点，易于在枪榴弹上实现与应用。