基于移动节点辅助定位的UWB室内定位方法

徐建华，张雨霖，韩勇强

（北京理工大学 自动化学院，北京 100081）

超宽带（Ultra Wide-band,UWB）技术是一种无线载波通信技术，它不采用正弦载波，而是利用纳秒级的非正弦波窄脉冲传输数据，具有数据传输速率高、抗多径干扰强、功耗低等特点[1]。视距条件下，其理论定位精度可达厘米级，近年来成为室内定位的研究热点[2]。采用UWB 技术定位，是通过UWB 设备之间的通信来获取相对位置信息，从而可以解算出待定位设备的位置信息。常用的UWB 定位方法包括到达时间法（Time of Arrival,TOA）、到达时间差法（Time Difference of Arrival,TDOA）、到达角度法（Angle of Arrival,AOA）、接收信号强度指示（Received Signal Strength Indication,RSSI）等[3]。其中TOA 和TDOA是基于测距的定位方法，具有稳定、易实现的特点，得到了大量应用。目前基于测距的方法大致分为三个步骤：获取各节点间距离，使用位置解算方法得到坐标初值，对坐标初值做滤波处理实现定位功能。从上述任一环节对定位过程进行优化，都能提升最终的定位效果。

UWB 设备通过检测信号传输时间计算节点间距离，传输时间测量越准确，测距精度越高。从硬件上提高UWB 设备的性能，是优化定位结果最直观的方法[4]。然而，UWB 设备的技术更新受限于通信原理的发展速度，使得大量UWB 定位研究着重于优化位置解算方法。常用的解算方法包括基于TOA 的最小二乘法、基于TDOA 的Chan 算法和Fang 算法等[5]，以及使用状态估计的各类概率模型方法，如卡尔曼滤波、粒子滤波等[6,7]。此外，为减小室内环境带来的误差，一些研究也针对不同环境提出了不同的方案。文献[8]通过理论分析误差带，使用最大绝对定位误差分析拓扑结构对定位结果精度的影响，提出了对拓扑结构的优化原则，能够根据环境特点，得出节点分布的最优拓扑结构。文献[9]使用误差图表示一个静态空间的分布定位误差，提高了室内定位精度。此外，行人的室内活动也对UWB 定位精度存在影响[10]。实际应用中，将UWB 与惯性测量单元（Inertial Measurement Unit，IMU）组合使用可以提高定位精度[11,12]，但是存在数据融合以及成本增加的问题。文献[13]在无线传感网的定位过程中运用了相似的辅助节点定位方法，文献[14]着重于解决辅助节点移动时的路径规划问题。

本文通过对传统解析方法的研究，针对具有基站-移动节点方式部署的场景，通过对低速及静止节点的判断，引入“退化节点”作为新基站，增加视距条件下基站数，提高UWB室内定位精度。确定可使用基站个数之后，通过设置增量队列筛选测距值，使用最小二乘法求解定位初值，然后使用扩展卡尔曼滤波器（Extended Kalman Filter,EKF）进行状态估计，得到较为准确的定位结果。

1 基于移动节点辅助定位的方法

基于移动节点辅助定位的方法分为判断可使用基站数、定位初值解算和使用EKF 进行状态估计三个阶段。首先在系统中设置分布节点标志位，当移动节点在分布式节点网络中被判断为静止（或速度很低）时，将该节点标志位置位，其当前坐标可作为辅助基站使用。将该移动节点加入到定位解算过程中，实现辅助定位的效果。分布式节点网络中，动态节点不断地加入和退出节点网络，参与定位的节点数目呈现动态变化。固定基站节点的坐标保持不变，该节点始终可用。在解算定位初值时，首先对待定位节点到各基站的测距值进行筛选，建立一个增量队列去除误差较大的测距值，然后使用最小二乘法解算出定位初值，将该定位初值作为EKF 的观测值。在EKF 算法中，建立合适的状态方程和观测方程，最后输出待定位节点的优化定位结果。

2 UWB 定位过程

2.1 测距值增量队列

本文设置一个增量队列来剔除测距值增量过大的异常点，从而提高定位精度。由于采样周期很短，节点低速移动时，理论上获取的相邻采样值的增量较小。如果其增量过大，则视作误差较大的异常点。基站为参与定位解算的各个固定节点，设Xi(i= 0,1…N)为移动节点到各个基站的距离，ΔXi(i= 0,1…N)为移动节点在一个采样周期内沿其与各个基站连线方向的位移增量分量，即移动节点到各个基站距离的增量：

其中，v为速度，Δt为采样周期。当采样频率为20 Hz时，Δt=0.05s。由于室内移动节点速度常低于2 m/s，一个采样周期内其移动距离小于0.1 m。相较于室内定位UWB 设备测距误差可达亚米级误差，可忽略一个采样周期内室内移动节点移动造成的定位误差。

设Xi(t)、Xi(t-1)(i= 0,1…N)分别表示移动节点到各个基站当前时刻t及上一时刻t- 1的距离，则：

记ΔX(t+1)为最新计算的增量矩阵，即：

计算增量矩阵时，前n个时刻增量队列形式如图2所示，设置增量队列长度为n=5，将其作为循环队列使用，队列中始终存储最近5 次的增量数据。每次采样结束后，求出ΔX(t+1)。

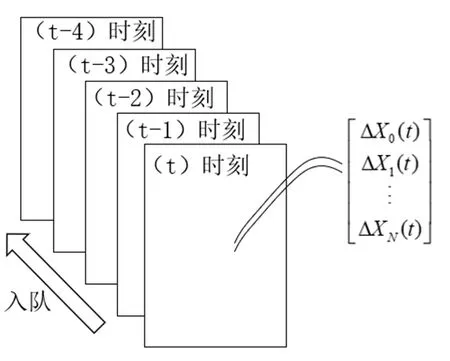
图2 增量队列示意图Fig.2 Diagram of the increment queue

记Y为增量判断矩阵：

其中，ζ为比例系数，用于控制接受增量的范围。得到增量判断矩阵Y之后，如果Y中所有元素均大于0，即：

式(5)表示使用当前采样测距值所计算的增量符合条件，这时将该增量放入队列，同时该增量将覆盖(t-4) 时刻的增量数据。系统接受该组测距值，并将其用于定位解算。

2.2 定位初值解算

使用解析方法求解式(6)所示的非线性方程组得到坐标值，通常的做法是将非线性方程组改写成线性方程组再进行计算。由于存在测距值误差、基站数冗余等原因，一般需要求解线性回归方程。多元线性回归方程的求解可以使用最小二乘法、梯度下降法、稳健回归等，其中最小二乘法由于不需要迭代求解且计算量小，是最常见的求解方法。

使用最小二乘法求解定位结果，记各个基站坐标为(xi,yi)，移动节点坐标为(x,y)，其到各基站的距离为di，可以得到：

将式(6)中各式两端平方，并用第一式减去后N式。对含有x、y项进行合并，将得到的结果写成矩阵形式：

并记作AX = B，用最小二乘法解式(7)：

2.3 扩展卡尔曼滤波器

卡尔曼滤波是线性高斯系统应用贝叶斯滤波方程而得到的显式解，将其应用在非线性系统时可能会出现结果不收敛的情况。EKF 的基本思想是利用泰勒级数展开将非线性系统线性化，然后使用卡尔曼滤波框架对信号进行滤波，其应用分为预测（predict）和校正（correct）两个步骤。

将室内移动节点运动模型近似为恒定转速和速度模型（ConstantTurnRateandVelocity,CTRV），并使用2.2节中计算得到的结果作为观测量，状态变量为待定位节点的坐标、速度、转向角、角速度。考虑以下离散时间非线性系统：

其中，第一行的状态方程为非线性，第二行的观测方程为线性，观测矩阵为系统噪声、为量测噪声。令：

离散时间步骤k与连续时间值t相关，可以得到当前时刻状态估计值，即：

计算式(11)积分的结果，可以得到非线性状态方程的表达式：

那么预测过程可表示为：

然后进行状态校正，首先计算卡尔曼增益：

其中，R为测量噪声协方差矩阵；Kk为卡尔曼增益。

其次求状态校正量，即：

最后更新误差矩阵：

输出校正后的状态量xk中的T[x′y′]，即为最终定位结果。

3 移动节点辅助定位算法

当一个移动节点处于静止或低速状态时，其定位精度高。将该节点解算得到的坐标加入到节点网络中，可以补充待定位节点的可利用基站个数。当视距范围内基站数量少时，对移动节点连续定位结果进行分析，在几个连续采样周期内，其二维坐标的离散度小，如图3所示。

图3 单节点连续采样坐标图Fig.3 Single node continuous sampling coordinate diagram

由于UWB 设备定位误差不呈正态分布[6]，对坐标两个维度分别进行分析，从而判断其是否可以被认定为“退化节点”，即其定位结果能否被其他节点当作基站坐标使用。同样地，定义一个长度为m的队列，存储m个连续采样坐标(xj,yj),j=0,1…m-1，得到x、y方向的均值μx、μy：

于是，可以得到x、y方向的方差：

当方差满足式(22)的条件时，接受该均值坐标(μx,μy)，并将其作为节点坐标。

其中，ηx、ηy为阈值，根据实验环境及精度要求确定。

本文所采用的UWB 定位系统并不从硬件上区分基站和标签，分布式节点网络可以得到任何其他节点到本节点的距离。任何节点在进行上述状态判断之后，都将坐标和标志位更新，并发布到节点网络上。为了避免重复计算，连续采样应该具有一段时间间隔。

单个节点定位流程如图4所示。系统启动之后，首先判断可使用的基站个数，解算得到节点定位结果。只有当系统处于连续采样周期内时，才进行移动节点的位置判断，观察其是否可以作为基站使用。当连续采样计算得到的坐标值个数达到队列长度，判断队列中的数据在两个方向上的方差是否小于阈值，若满足条件则将标志位置位，并将其发布到节点网络上。

图4 单节点一个定位周期的流程图Fig.4 Flow chart of a positioning cycle for a single node

4 实验验证

4.1 实验环境

在室内环境中选取大小约为3 m×9 m 的长方形区域，布置三个固定节点作为基站，其坐标分别为（0，0）、（0，8.28）、（1.6，8.28），单位：m。设置两个移动节点，一个节点放在实验者身上，通过该节点的USB端口输出数据到电脑端。另一个节点放在小车平台上，移动速度较低，作为辅助节点使用。

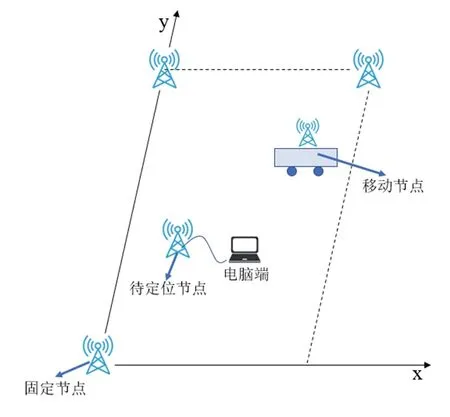
图5 节点分布示意图Fig.5 Node distribution diagram

实验 UWB 设备采用 Nooploop 公司设计的LinkTrack S 模块，该模块数据帧输出频率可达50 Hz。实验过程中，使用模块的分布式节点网络模式进行系统搭建，使网络中的每个节点都可以输出它到任何其他节点的距离值。

图6 移动节点Fig.6 Mobile nodes

4.2 测距值对定位结果的影响

基于测距的定位方法对于节点间测距值十分敏感，很小的单个测距误差也可能导致定位结果的较大偏差。考虑到该UWB 设备测距误差可达亚米级，对测距值加以随机误差进行仿真实验，由3σ原则取σ=0.33。随机取一个定位点，进行100 次定位计算，得到结果如图7所示。由于定位结果随测距值变化很大，对测距值的筛选是很有必要的。

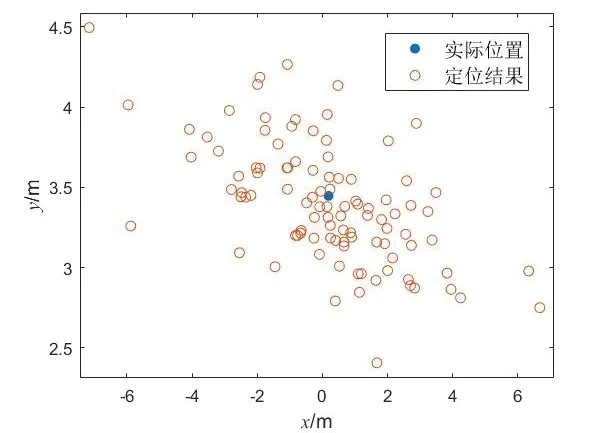
图7 测距误差对定位结果的影响Fig.7 The influence of ranging error on positioning

常规异常值剔除方法较多，如3σ原则、卡方检验、箱线图法等。与常规方法中对完整数据进行异常值剔除有所不同，本文实验中对异常值的剔除需要满足实时性，即实时判断数据是否为异常值。将本文提到的增量队列筛选方法与卡方检验、3σ原则进行比较，在保证采样点足够及坐标相对连续的情况下，比较三种方法处理后的定位均方根误差、最大定位绝对误差和计算时间。其中，计算时间为单次实验使用某一方法的计算总时间，卡方检验的卡方分布因子阈值设置为5。

由表1 可知，卡方检验的定位误差较小，但是计算时间太长，大量的矩阵计算无法保证定位的实时性。3σ原则计算时间较短，但是定位误差稍大，且需要存储大量数据用于计算。增量队列筛选方法计算时间最短，可以满足实时定位的需求，且每次计算所需数据量少。

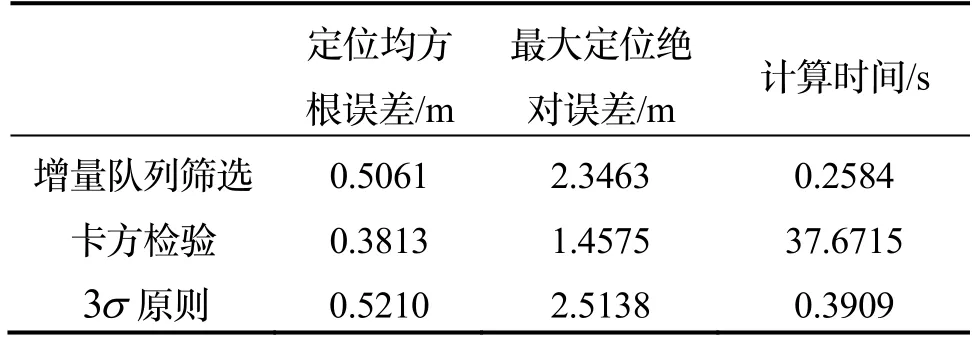
表1 三种异常值剔除方法性能对比Tab.1 Performance comparison of three outlier removal methods

4.3 无辅助定位实验效果

实验开始前，先对UWB 设备进行标定。无辅助定位实验指在不加入移动节点的情况下进行定位测试，即不更新第3 节中所述标志位，只依靠现有固定节点进行定位解算。实验前已经画出待定位节点移动的真实轨迹，实验中对最小二乘法、使用增量队列筛选和加入增量队列后使用EKF 的方法进行对比。

室内环境下，多径效应和金属物体对信号衰减影响明显。当用于定位的节点较少时，可能会出现较大的定位误差。由于增量队列剔除了异常点，所以采用EKF方法得到的采样点会减少。按照采样点采样时的顺序进行绘图比较，从图8-9 和表2 可以看出，采用改进算法得到的定位结果，误差明显减小。与最小二乘法相比，使用增量队列筛选后定位均方根误差减小了7.14%，最大定位绝对误差减小了26.95%。加入增量队列后使用EKF 方法，相比于最小二乘法其定位均方根误差减小了10.02%，最大定位绝对误差减小了64.47%；相比于增量队列筛选方法，其定位均方根误差减小了3.1%，最大定位绝对误差减小了51.37%。异常点的剔除使得定位结果的最大误差显著降低，消除了曲线上的突变，使得定位结果更加平滑。EKF 方法中状态变量估计曲线如图10所示，v为速度、θ为角度、ω为角速度。

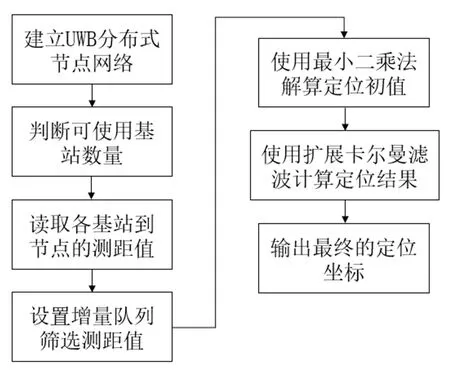
图1 基于移动节点辅助定位的流程图Fig.1 Flow chart based on mobile node auxiliary positioning

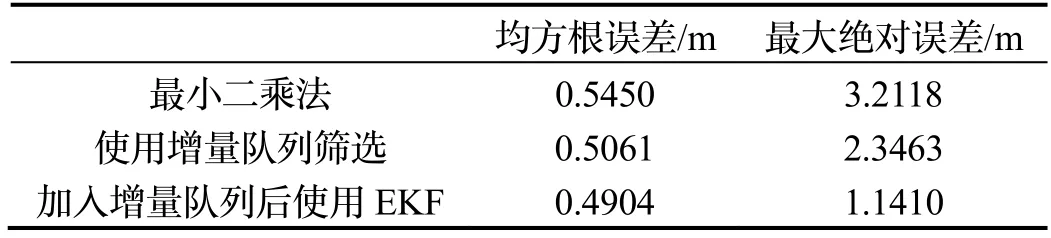
表2 三种算法下的定位误差对比Tab.2 Positioning error comparison of three algorithms

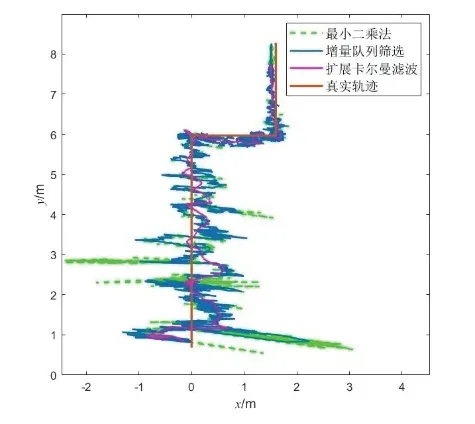
图8 无辅助定位实验轨迹图Fig.8 Experimental trajectory diagram of non-auxiliary positioning experiment

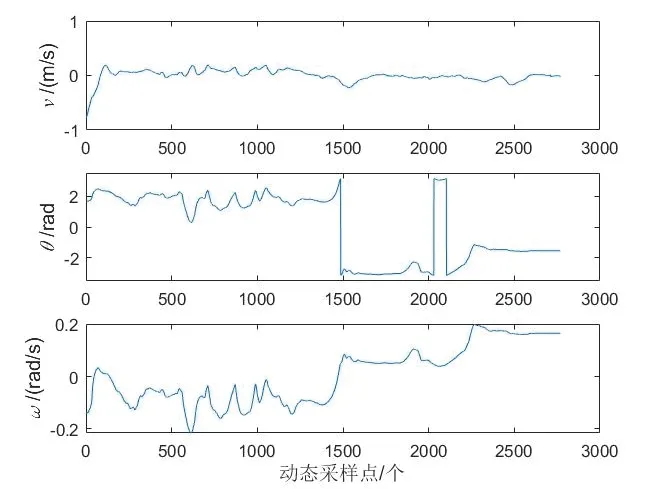
图10 无辅助定位实验EKF 方法中状态变量估计曲线Fig.10 State variable estimation curves in EKF method of nonauxiliary positioning experiment

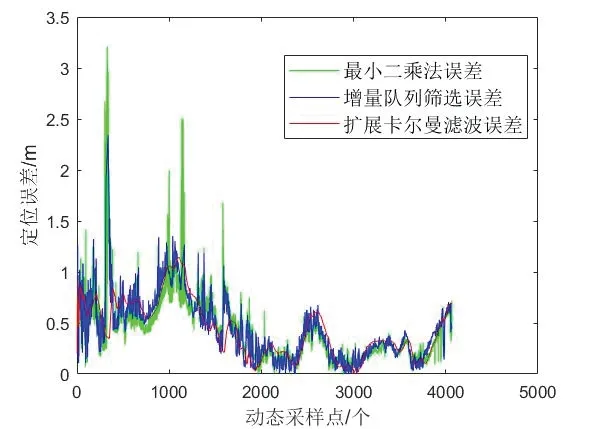
图9 无辅助定位实验定位误差Fig.9 Positioning error in non-auxiliary positioning experiment

4.4 移动节点辅助定位实验效果

将第3 节所述标志位使能，加入移动节点辅助定位功能。配置系统参数，采用第3 节中单节点定位周期流程进行实验。分别使用最小二乘法、Chan 算法和移动节点辅助定位的方法进行实验，对实验采样数据进行分析处理，得到其定位结果及误差。

当移动节点（小车）进入低速（静止）状态时，其标志位翻转。图11 给出了某个时刻加入到节点网络的辅助节点的实际位置，将解算出来的坐标用于待定位节点的定位过程，得到采用不同算法进行实验的结果。从图11-12 和表3 可知，基于移动节点辅助的定位解算方法相比于最小二乘法和Chan 算法，其均方根误差分别减小了15.89%和16.45%，最大绝对误差分别减小了60.99%和62.77%。图13 给出了EKF 方法中各状态变量估计值的变化情况。

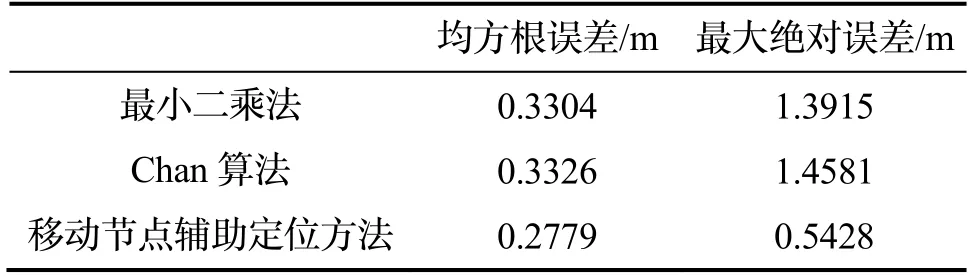
表3 不同算法下的定位误差Tab.3 Positioning errors under different algorithms

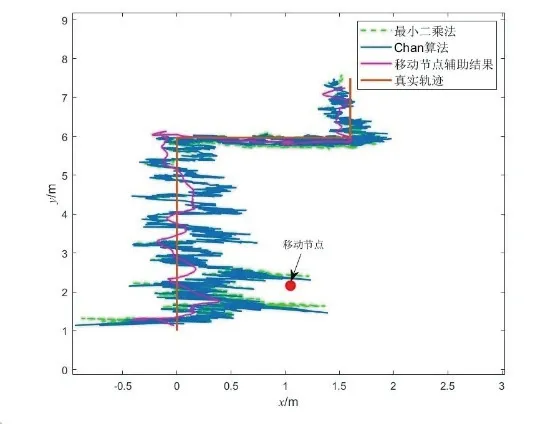
图11 辅助定位实验轨迹图Fig.11 Experimental trajectory diagram of auxiliary positioning experiment

图12 辅助定位实验定位误差Fig.12 Positioning error of auxiliary positioning experiment

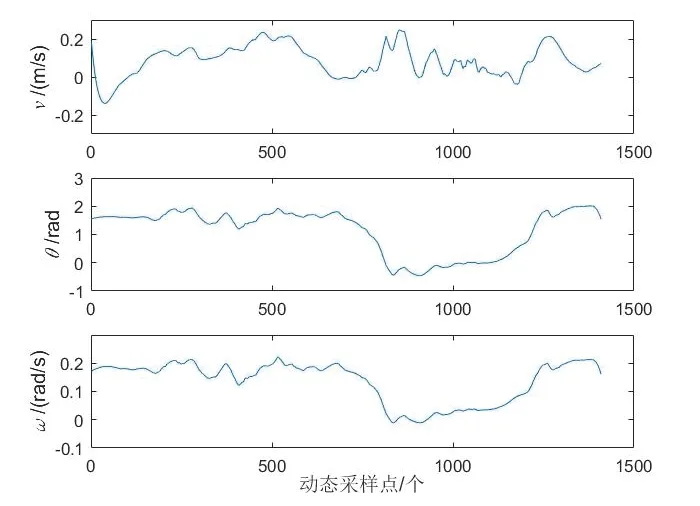
图13 辅助定位实验EKF 方法中状态变量估计曲线Fig.13 State variable estimation curves in EKF method of auxiliary positioning experiment

对比4.3 节和4.4 节的实验结果，可见使用移动节点辅助定位的方法能够使得定位误差更小。在加入增量队列筛选后，对是否有移动节点辅助定位进行多次对比实验，得到如表4所示的结果。

表4 有无辅助定位时的定位误差Tab.4 Positioning error with or without auxiliary positioning

对比表中数据可以得到，加入移动节点辅助定位可以有效降低定位误差。由于辅助节点可以动态加入，能够增加视距范围内有效基站数，提高定位解算冗余度，从而减小定位误差，提高室内定位的精度。另一方面，移动节点辅助定位的方法一定程度上降低了对固定节点的依赖性，可以减少固定基站部署，从而降低成本。

5 结论

本文设计了一种基于移动节点辅助定位的UWB室内定位方法，通过引入辅助节点，增加参与定位的基站数量，从而提高待定位节点的定位精度。该方法首先判断可使用基站数，设置一个增量队列，用于对各个测距值进行筛选，剔除异常点。使用最小二乘法解算坐标，得到定位初值。利用该定位初值，通过EKF进行状态估计，得到最终的定位结果。实验结果表明，本文方法可以减小定位误差，消除定位曲线异常突变，提高定位精度，具有一定的工程应用价值。