基于长短期记忆网络的半潜平台波浪爬升预报

李 琰， 肖龙飞,3， 魏汉迪,3， 寇雨丰

(1. 上海交通大学 海洋工程国家重点实验室，上海 200240； 2. 上海交通大学 海洋装备研究院，上海 200240； 3. 上海交通大学 三亚崖州湾深海科技研究院，海南 三亚 572024)

在恶劣海况下，波浪沿立柱的爬升效应会导致强非线性砰击和越浪风险，对海洋平台局部结构安全构成极大威胁[1].采用时间序列方法、机器学习等手段[2]对未来波浪爬升情况进行极短期在线预报，可在极端海况下提供及时预警，对平台作业和人员安全具有重要意义.

目前，波浪爬升的在线预报研究大多集中于海岸工程，通常在经验公式的基础上，结合神经网络、模糊数学等现代方法建立不同的预报模型.Lee等[3]通过采集摄像获得波浪爬升图像信息，结合入射波统计信息建立经验公式，测试集预报结果拟合系数R2仅为0.559；Power等[4]基于实验室和实测数据，建立基因表达式编程模型，与传统经验公式相比准确度有所提升，预报结果拟合系数R2为0.82；Bakhtyar等[5]通过自适应网络的模糊推理方法对冲刷带的波浪爬升变化进行建模预测，使预报精度在规则波与不规则波情况下均有显著提升；Abolfathi等[6]基于M5模型树算法建立波浪爬升模型并确定其最佳特征参数，拟合系数R2可达0.97，且与传统人工神经网络结构相比，该方法极大缩短了训练时间；Bonakdar等[7]选用非破碎规则波在不同水深下进行垂直立柱的波浪爬升试验，基于M5模型树和非线性回归方法建立了波浪爬升高度预报公式，拟合系数R2达到0.94.

区别于海岸工程中的固定结构物，浮式海洋平台波浪爬升问题中的立柱与波浪相互作用过程会同时产生明显的波浪绕射和辐射效应[8]，目前尚未发现相关在线预报研究.本文基于求解时序问题的长短期记忆(LSTM)神经网络结构提出波浪爬升在线预报模型，应用于半潜式平台波浪爬升极短期预报，并通过模型试验数据测试验证该模型的可行性.

1 LSTM预报模型

由于平台运动和入射波相互耦合作用对浮式海洋平台的波浪爬升高度有影响，为准确获得预报波浪爬升高度的映射关系，选取入射波与平台垂向运动(垂荡、横摇、纵摇)时历数据共同作为深度神经网络输入信息，通过最小化损失函数对深度神经网络中的相关参数进行多次迭代更新，最终实现平台波浪爬升高度预报.

在预报方式上，通过将固定长度的波浪和平台垂向运动时间序列作为输入量对波浪爬升高度(h′)进行预报，具体原理如图1所示.在任意时刻t，利用t-40时刻到t-20时刻的多变量输入序列片段可获得t时刻的波浪爬升高度预报值，即通过长度为20 s的历史数据信息片段获得提前预报量为20 s的预报结果[9].

图1 模型输入输出映射关系Fig.1 Mapping of input and output of model

在平台波浪爬升问题中，t时刻波浪爬升高度会受到t-1时刻波浪数据和平台运动状态影响，存在明显的时间依赖性，因此波浪爬升预报属于典型的时间序列预测问题.LSTM是一类用于处理序列数据的神经网络模型，基本结构如图2所示.LSTM通过调整内部单元状态实现对历史信息的储存，并在此基础上引入“门”结构对信息进行处理，即分别通过输入门i、输出门o和遗忘门f完成单元内信息的更新和传递[10].在任意时刻t，LSTM网络单元的输入变量包括外部输入数据xt，上一时刻的LSTM网络单元输出值ht-1，以及上一时刻的单元状态ct-1；输出变量包括当前时刻的LSTM网络单元输出值ht和单元状态ct，其中ct为更新门函数，用于控制网络单元内部存储信息并更新；ht为经过处理后的最终输出内容.各控制门均采用Sigmoid函数(σ)实现相应功能，当各控制门完全打开时，信息则可全部存储并进行处理；当各控制门关闭时，信息则无法被传递.此外，LSTM单元中分别增加处理层g和h，与输入门i和输出门o共同实现单元状态ct的输入和输出信息更新.

因此，LSTM模型中隐藏层神经元的计算式可表示为

gt=tanh(Wc·[xtht-1]+bc)

(1)

ft=σ(Wf·[xtht-1ct-1]+bf)

(2)

it=σ(Wi·[xtht-1ct-1]+bi)

(3)

ot=σ(Wo·[xtht-1ct]+bo)

(4)

ct=ftct-1+itgt

(5)

ht=ottanh(ct)

(6)

式中：gt为处理后的输入信息；Wc和bc分别为gt的权值矩阵和偏置项；ft为遗忘门函数，用于控制网络单元中需丢弃的错误预测信息；Wf和bf分别为ft的权值矩阵和偏置项；it为输入门函数，用于控制网络单元中输入的新信息；Wi和bi分别为it的权值矩阵和偏置项；ot为输出门函数，用于控制输出信息；Wo和bo分别为ot的权值矩阵和偏置项.

深度神经网络结构如表1所示，包含2层LSTM隐藏层及2层全连接层.根据平台运动和波浪相关参数，设置输入的波浪和平台运动数据长度为128，由于波浪爬升问题具有明显的非线性特征，所以选择双层LSTM结构实现对其非线性特征的拟合，通过经验及预实验确定神经网络中的隐藏节点数.

图2 LSTM单元结构示意图Fig.2 Structure of LSTM cell

表1 波浪爬升预报模型神经网络结构

学习率作为神经网络中重要的超参数，决定了模型的训练速度以及最终的训练效果.因此在训练过程中基于训练次数不断调节学习率以实现动态下降，训练过程中损失函数在一定回合不发生变化后，学习率降低为初始值的10%.

为防止训练过程中发生过拟合，在神经网络结构中添加Dropout层[11].Dropout可以在训练过程中将神经网络单元按照一定的概率暂时丢弃，从而有效减弱神经元节点之间的联合适应性，增强模型的泛化能力.

2 训练与测试数据

为验证预报模型的准确性，选取半潜式平台气隙性能模型试验数据进行训练和测试，该试验在上海交通大学深水试验池进行.试验布置及平台模型如图3和图4所示.

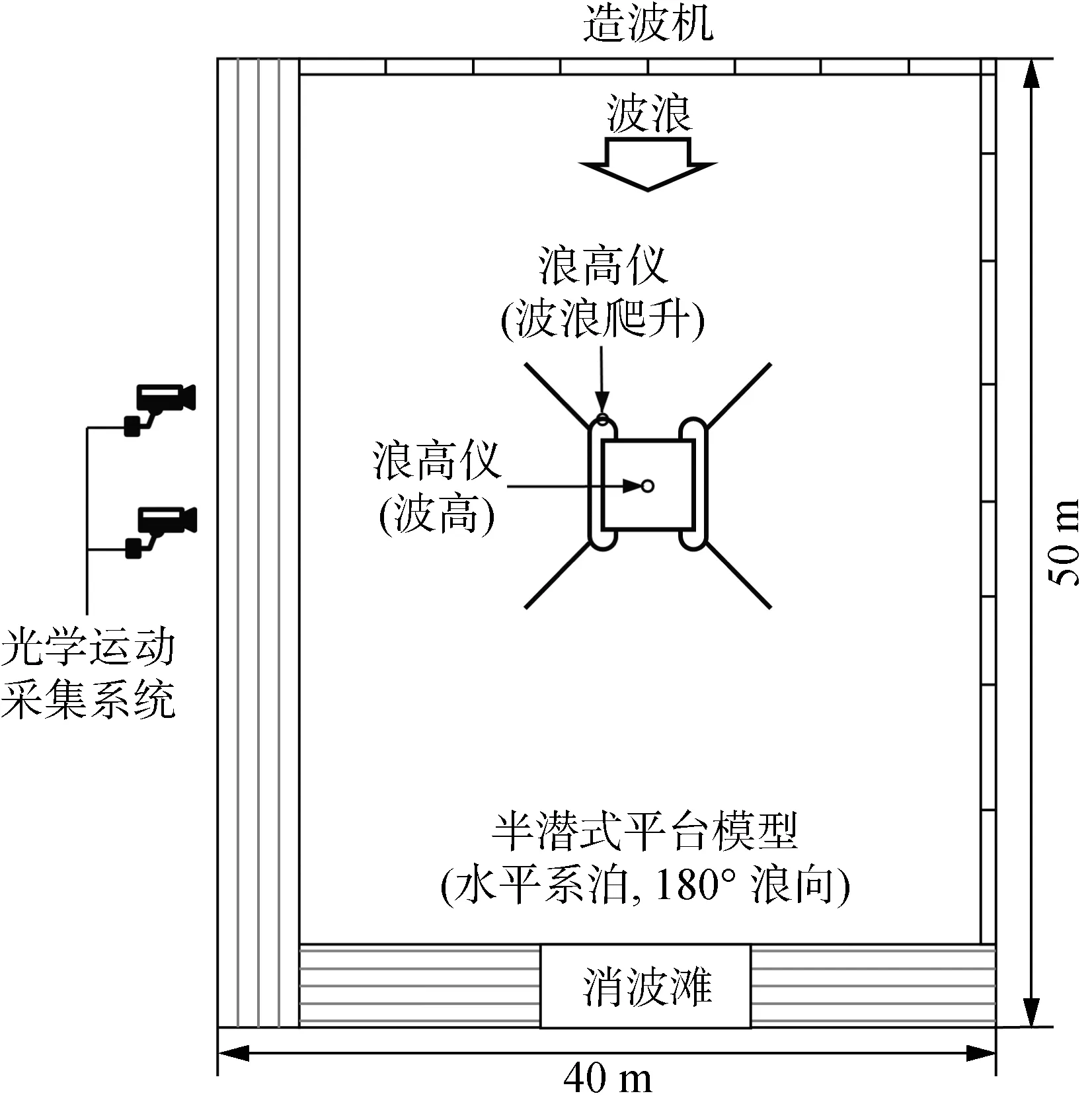
图3 试验水池布置图Fig.3 Deepwater offshore basin layout

图4 半潜式平台模型Fig.4 Semi-submersible model

半潜式平台主尺度如表2所示，缩尺比设置为 1∶56.试验中的平台模型采用4点水平系泊系统，系泊缆与平台坐标轴成45°对称布置.平台六自由度运动数据通过光学测量系统进行采集，平台中心位置布置浪高仪用于采集入射波的波浪数据，平台迎浪位置立柱前端布置浪高仪用于采集波浪爬升数据.

表2 半潜式平台主要参数Tab.2 Main particularities of semi-submersible platform

试验中总计开展不规则波迎浪工况40组，依据联合北海海浪大气计划(JONSWAP)标准波谱实现对应波浪的模拟，各海况对应有义波高(Hs)、谱峰周期(Tp)、谱峰因子(γ)以及随机种子数如表3所示.其中，W1和W2工况各包括4组试验数据，W3和W4工况各包括16组试验数据.试验中采样频率为100 Hz，各组数据采样点数量超过 160 000 点.考虑各工况试验数据量，W1和W2工况各选择3组数据，W3和W4工况各选择14组数据共同作为训练数据用于深度神经网络训练，剩余6组数据作为测试数据集.

表3 波浪参数(JONSWAP)Tab.3 Environment matrix(JONSWAP)

浪高仪和平台运动数据采集点均滞后于立柱位置，因此需要对波浪爬升数据进行相位调节，以平台运动数据为基准保证各组数据时间对应准确.然后根据模型缩尺比将试验数据换算为实型值.由于原始数据量较大，为提高模型训练速度的同时避免数据信息损失，对原始数据进行下采样处理.如图5所示，下采样处理后的数据与原始数据保持了较好的重合度，在降低数据量的同时仍可有效传递原有数据信息.

图5 数据下采样处理效果对比Fig.5 Comparison of downsampling and original data

3 预报结果与分析

将选取的34组工况数据作为训练数据，分别在提前预报量为0、6和12 s时获得3个不同的基于LSTM的深度神经网络模型，然后对测试工况下的立柱波浪爬升高度进行预报，并与试验测量结果进行对比分析.选取4种海况下提前预报量为6 s的时历数据，如图6所示.由于完整时历数据量过大，所以在序列起始、中间和末尾各选取300 s的预报结果进行对比.

结果表明，对于半潜式平台迎浪方向的波浪爬升情况，基于LSTM的深度神经网络模型均取得了较好的预报效果，能够较准确地描述波浪爬升趋势与爬升高度.随着提前预报时长的增加，波浪爬升预报结果的相位精确度保持稳定，爬升高度极值精确度有所降低，且预报结果偏低.

计算波浪爬升高度试验值与预报值的拟合系数R2，可以获得基于LSTM的深度神经网络模型的预报精度，结果如表4所示.随着提前预报时长的增加，各海况下模型预报精度有所降低，提前预报量为6、12 s时的平均预报精度整体降低幅度分别为4.01%、12.82%.随着海况编号的增大，模型预报精度也呈下降趋势.考虑到W3与W4海况下的训练数据量远多于W1与W2海况，在提前预报时长增加的情况下，W3与W4预报结果仍能保证较为稳定的预报性能，准确度降低幅度较小.

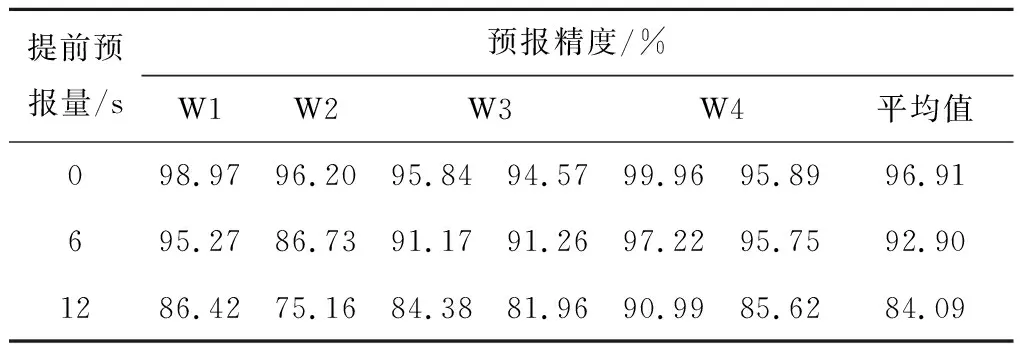
表4 不同测试工况下波浪爬升高度预报精度统计结果Tab.4 Prediction accuracy statistics in different test cases

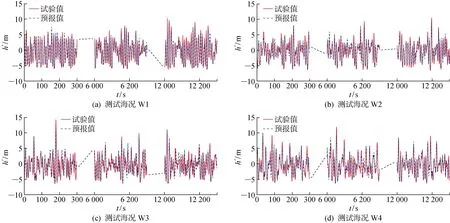
图6 不同测试海况下提前预报量为6 s时立柱波浪爬升预报与测量结果对比Fig.6 Comparison of measured and predicted wave run-up in different test cases at a forecast duration of 6 s

表5 不同测试工况下波浪爬升高度统计值对比Tab.5 Comparison of wave run-up statistics in different test cases

通过对比立柱波浪爬升高度最大值、最小值和有义值等统计值结果，可以进一步对深度神经网络的预报性能进行分析，不同测试工况下波浪爬升高度统计值对比如表5所示.在提前预报量为0 s时，波浪爬升高度的最大值精度大于85%，且在波高较小的情况下可达97%；最小值预报精度大于93%，部分工况达99%；有义值精度大于97%.结果表明，该模型具有较好的预报准确性，可在获得平台运动和波浪数据的情况下，直接获取波浪爬升高度，对模型试验和实测均具有较高的应用价值.在提前预报量为6 s时，波浪爬升高度最大值、最小值和有义值的相对误差分别不高于19.69%、3.72%、8.70%，尽管预报精度有所降低，但模型可有效应用于波浪爬升高度的极短期预报，对可能发生的负气隙和砰击现象提前做出反应.在提前预报量为12 s时，最大值、最小值和有义值的相对误差分别不高于30.66%、3.81%、12.32%，虽然整体预报精度进一步降低，但具有较长的预报提前量使得该模型具有更广泛的应用空间.此外，最大值和最小值等随机性较强的统计量对波浪参数较为敏感，训练数据量的增加无法提高其预报的准确程度，但可以有效提高有义值等统计结果的准确性.

波浪爬升最大值和最小值具有较强的随机性，因此对模型预报结果的极值概率分布情况进行分析，不同测试工况下波浪爬升高度极值(hmax)概率密度分布如图7所示.在不同工况下，各提前预报量的预报结果的波浪爬升高度极值分布均取得了较好的拟合效果，且对于实际更为重要的较大波浪爬升高度极值的预报精度更高.提前预报量为0 s与6 s的波浪爬升高度极值概率分布结果较为接近，表明此时基于LSTM的深度神经网络模型对提前预报时长变化不敏感.

图7 不同测试海况下波浪爬升高度极值概率密度分布结果Fig.7 Probability density distributions of extreme wave run-up in different test cases

4 结论

基于LSTM建立半潜式平台波浪爬升预报模型，通过模型试验采集训练与测试数据，将波浪与平台垂向运动作为特征数据输入，获得不同提前预报量下的预报值，结果表明：

(1) 波浪爬升预报模型对平台立柱波浪爬升高度的极短期预报具有较好的效果，提前预报量为6 s和12 s时整体预报精度分别为92.90%和84.09%，最大值预报结果的相对误差不高于19.69%和30.66%，最小值预报结果的相对误差分别在3.72%和3.81%以下.

(2) 随着预报时长增加，预报精度有所降低且预报结果偏低，波浪爬升高度最大值和最小值预报精度受海况影响较为显著，但对训练数据量规模大小不敏感.

(3) 波浪爬升预报模型对更为重要的较大波浪爬升高度具有较好的学习效果，在提前预报时间6 s内，能实现稳定的预报输出并且具有较好的准确性.

LSTM模型在提前预报量较大时的准确性降低，且训练数据集源于模型试验，其工程实际预报性能有待验证.后续将通过神经网络参数优化和方法改进，提高预报结果准确性并延长预报提前量，同时结合现场实测数据进行训练测试，以更好指导工程实际.