基于迭代优化的两帧随机相移干涉术

刘畅，杜虎兵，冯雷洁，严兴旭，张高鹏

（1 西安工业大学 机电工程学院， 西安 710021）

（2 中国科学院西安光学精密机械研究所， 西安 710119）

0 引言

两帧随机相移技术在应用过程中由于能降低相移器的严格标定要求，并可以减少机械振动、环境空气扰动或温度变化等不利因素对测量的影响，因此在动态或瞬变现象三维传感场合具有广泛的应用［1-2］。KREIS T M等［3］开展了两帧随机相移干涉图相位解调的研究。该方法利用傅里叶变换，并结合简单的代数运算可以快速提取条纹图中引入的未知相移，但是当引入的相移量较小时或条纹图受噪音污染较大时，其方法常常会失效。应当说明，两帧随机相移技术由于使用的条纹图数目少，而求解未知量的数目多于求解方程的数目，致使该类问题是一个病态的反问题，从而发展一种实用的两帧随机相移解调技术充满了挑战和不确定性。因此在KREIS的研究工作之后的近十年间，两帧随机相移解调技术的发展有所停滞。两帧随机相移技术突破性的工作始于VARGAS J等［4-6］。2011年，VARGAS J等连续提出了多种用于两帧随机相移条纹图解调的实用算法，并建立了两帧随机相移条纹图相位解调技术的范式，即首先对条纹进行归一化处理或滤除背景，然后通过一定的正则化技术求解相移进而搜索感兴趣的相位，或者根据采集的条纹图构造其正交条纹图直接计算相位。此后，二帧相位解调技术在全球范围内得到了快速发展，并发表了一系列的二帧解调技术。其中，Gram-Schmidt正交化相位解调技术将摄取的两帧条纹图视为独立的正交向量，可以简单、迅速、高精度地恢复测量相位，并成为广泛应用的二帧相位解调技术之一。但该方法对噪音和背景的变化敏感。对此，TIAN Chao等［7］提出了在局部通过相位拟合和全局优化搜索了相移的技术。该方法利用差分进化算法能可靠地估计相移，具有优良的性能，主要缺点是需要对条纹图进行复杂的正则归一化处理，从而由于归一化处理的精度不足限制了该技术的进一步应用。针对现有二帧技术在应用过程中存在着条纹数目、特殊的预设要求等限制，2019年，CHENG Zhongtao等［8］基于相移与条纹图振幅方差的演变规律，发展了利用优化方法搜索相移的技术。该技术精度高、通用性强，但要求在相位解调之前对采集的条纹图进行背景预滤波处理。实际中，由于物理实验中的缺陷难以被精确地建模，因此进行预滤波处理时，滤波算法很难对光强的频率分布做出正确的假定。因此，上述基于预滤波的两帧随机相移技术在相位解调时其精度常常受到预滤波效果的影响，并限制了测量速度的提高。

针对预滤波导致的误差严重地影响相位重建的精度的问题，当前许多学者将注意力放在了背景残差抑制方面。文献［9-10］试图结合李萨如图拟合最小二乘迭代相移算法绕过预滤波。该类技术由于实现了无需预滤波的二帧随机相移条纹图相位解调，属于解调二帧随机相移条纹图的第二类范式。在这些方法中，首先通过李萨如图拟合或其他方法估计粗略的相位，然后利用该初始相位，逐帧地通过求解一系列线性方程估计相移，进而反复迭代上述过程，直至收敛至预定义的精度，最终得到精确地相位解。其方法通常需要迭代两三次，可以快速地获得精确的相位，主要缺点是迭代过程中要求条纹图的背景照度和对比度必须在空间上保持恒定。此外，对于具有非正弦光强分布的实际条纹图，李萨如图拟合算法计算结果并不稳定。

最近，基于主成分分析法（Principal Component Analysis， PCA）［11］及上述的最小二乘迭代策略，ZHANG Hangying等［12］提出了另一种无需预滤波的两帧随机相移算法。该方法首先通过两个采集的条纹图的减运算构建了第三帧条纹图。然后利用经典的主成分分析法估计初始相位，进而应用最小二乘迭代方法细化测量结果。然而PCA算法［13］基于统计学意义，通常即使提供了大量的条纹图，也会产生较大的相位解调误差。因此，由于提供了较差的初始相位，可能大大降低了该方法的精度，甚至使该方法无法工作。

综上可知，二帧相移技术最主要的问题是最大程度地减少残差背景的影响。对此，本文提出一种无需预滤波的两帧随机相移技术。本文方法基于先进迭代算法（Advanced Iterative Algorithm， AIA）［14］的思想，针对迭代算法的收敛结果易受初值的影响，利用条纹图的相关运算，快速估计初始相移，然后利用二帧相移算法搜索相位，针对二帧条纹图残差背景对测量精度的影响，利用解调过程中的过程参数，不断地更新估计背景，将残差背景对相位解调的影响降至最低。本文的方法将标准的AIA算法推广至两帧条纹图的场合，为两帧相移干涉技术提供了一种有效的途径。提出的算法步骤可以总结为：1）去除条纹图的空域均值，估计初始相移；2）根据相移估计相位；3）利用最小二乘获得背景和更新后的相移；4）利用求得的背景更新光强；5）迭代上述过程直至收敛。

1 基本原理

通常，采集的两帧随机相移干涉图可以建模为

式中，A(x，y)和B(x，y)是背景强度和调制振幅，其空间上逐点变化，但在时域上逐点恒定；ϕ(x，y)和δt是两个相移条纹图之间的测量相位和未知时域载频。不失一般性，假定δ1=0。为了简单起见，以下省略了空间坐标(x，y)。从采样条纹图中减去空域均值，此时，两帧相移干涉图可表示为

设为δ的估计值。建立惩罚函数

其中S为条纹图的像素的总数目。F是二次函数，值域为正实数，有最小值0，因此由

将条纹图I1和I2分别重写为MN×1的向量I1和I2（M、N为条纹图的大小），此时F可表示为

将式（6）中获得的F的表达式代入式（5），可得

式（7）与文献［15］的结论相同，但采用了不同的推导方式。式（7）分母总是大于分子，因此可以可靠地估计初始相移为

进而利用二帧相移算法估计相位为

上述正交条件是近似满足的，且忽略了残差背景的影响，为了进一步提高求解精度，本文提出利用迭代策略对式（9）进一步细化。具体的讲，首先使用第二帧条纹图在空域估计相移，考虑到干涉条纹图的背景A是逐点变化的，为了减少背景空域变化对求解的影响，本文将采集的第二帧条纹图在空间上分解为若干个条纹图子图，然后任选一块条纹图子图，并假定其中相邻像素点之间的背景A和振幅在空间上恒定。设选取的条纹子图的大小为k×k，并将条纹子图块中的光强和对应的相位向量化，记为I1s，I2s，…，Ik2s和ϕ1，ϕ2，…，ϕk2，则选取的条纹图子图块可以表示为

式中，a=A，b=Bcosδ，c=−Bsinδ。在最小二乘意义下有

求解未知数可得

根据式（12），更新相移为

现有的文献通常忽略了上述求解的过程信息a，为了最大化减少背景的影响，本文提出利用原始光强Ir减去求得的背景a，更新式（2）中去除背景后的光强I1和I2，即

进而将更新后的I1、I2和求解的相移δ＇带入式（9），迭代式（9）～（14），其收敛标准可以定义为

式中，q为迭代次数，ε为预定义的收敛精度。当满足收敛准则时，即可得到精确的相位分布。本文方法具体的流程图如图1所示。

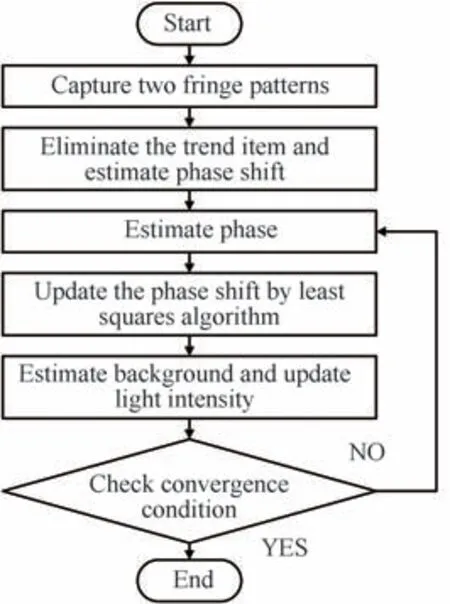
图1 本文方法的流程Fig.1 Flow chart of the proposed method

2 仿真实验

为了验证本文的方法，首先进行了仿真实验。文中所有数据处理采用Intel（R） Xeon（R） W-2123处理器和MATLAB R2021a软件。根据式（1），定义空间变化的背景强度和振幅为a=10−5×定义相位方程为peak函数，预设相移为δ=1.6 rad。图2分别给出了模拟生成的添加了信噪比为35 dB随机噪音的两帧条纹图（大小为340×340像素）及参考相位。

图 2 模拟的两帧相移条纹图和参考相位Fig.2 Simulated two-frame phase-shifted interferograms and the reference phase

考虑到PCA&LSI方法是无需预滤波的二帧算法的典型代表，而CV方法在现有的需要预滤波的二帧算法中具有优良的性能，为了比较说明本文方法的性能，本文将提出的方法与PCA&LSI方法［12］和CV方法［8］的结果在相位重建性能方面进行比较。本文的相位去包裹方法参见文献［16］。具体结果如图3所示。本文方法的测量相位、PCA&LSI方法的测量相位、CV方法的测量相位见图3（a）、图3（b）、图3（c）。本文方法、PCA&LSI方法、CV方法的均方根误差见图3（d）、图3（e）、图3（f）。

图 3 相位重建仿真Fig.3 Simulation for the phase reconstruction

本文方法、PCA&LSI方法和CV方法相应的处理时间分别为0.080 6 s、0.248 8 s、2.460 7 s。可知，本文方法的速度相比PCA&LSI方法提高了约3倍，相比CV方法提高了约30倍。其原因是，PCA&LSI方法视条纹图的背景和振幅的时域与空域均逐点变化，相比本文方法增加了计算第二帧条纹图的背景和振幅的要求。而CV方法由于需要进行费时的优化搜索，因此其过程耗时较多。

结合图3（d）～（f）三种方法的误差分布可知，本文方法的精度优于PCA&LSI和CV方法，重建质量最好。同时由于采用了条纹子图计算相移，本文方法用时最短。根据本文的测试经验，通常条纹图子图的大小取原始条纹图大小的一半即可得到较好的效果。

考虑到上述测试过程的随机性，为了证明本文方法具有高的可靠性，本文进行了20次独立实验，比较了PCA&LSI方法、CV方法和本文方法的均方根误差（Root Mean Square， RMS）。由图4（a）可以看出，三种方法均具有高的测量稳定性，但本文方法相位均方根误差最小。

另外，本文又测试了三种方法的误差随相移的变化规律。考虑到三种方法相移求解范围为[0，π]，本次测试中相移的变化范围设定为0到3。图4（b）表明，CV方法的解调误差随相移变化波动较大。另外，尽管PCA&LSI方法与本文方法在相移较大时解调误差相当，但在本次仿真分析中，本文方法的综合性能相比其他两种方法更好。

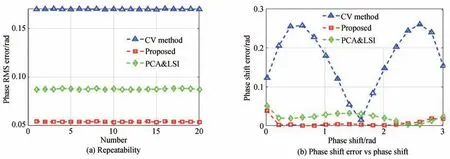
图 4 三种方法的演化误差Fig.4 Evolution of the error of three methods

为了验证本文方法的可靠性，在35 dB的高斯噪音下，计算了相移分别为0.82 rad、1.42 rad、2.02 rad时，本文方法、PCA&LSI和CV方法的相位均方根误差，结果如表1所示。

表1 相位均方根误差（dB）Table 1 The RMS error of phase（dB）

由表1可知，随着相移的增加，PCA&LSI算法的相位均方根误差约是本文方法的相位均方根误差的1.5倍，而CV算法的相位均方根误差约是本文方法的相位均方根误差的3.5倍。显然，CV方法的相位均方根误差最大，表明该方法重建相位时波动较大。相比可知，本文方法的性能最稳定。其原因是，本文方法由于提供了一个较好的初值，在迭代收敛过程当中，能更快速的收敛，因此获得了最好的综合性能。表2给出了不同信噪比下三种方法重建相位的均方根误差。

表2 均方根误差（dB）Table 2 The RMS error（dB）

表2表明，CV方法均方根误差较大，即该方法对噪音敏感。主要原因是该方法基于优化搜索的原理，当噪音水平较高时，噪音使得优化过程变得复杂，并影响了正确结果的搜索。相比之下，本文使用了大量的估计相位数据，在最小二乘意义下估计相移，由于大量数据的均化作用，很好的抑制了噪音对求解相移的影响，表明本文方法对噪音不敏感。

3 测量实验

为了进一步比较本文方法的性能，进行了实际测量实验，获得了三套条纹图，包括开形条纹图（图5（a）～（b））、闭形条纹图（图5（d）～（e））和复杂条纹图（图5（g）～（h）），每套含有7帧条纹图。复杂条纹图是由不规则曲面得到。实验时，本文采用PCA&LSI方法、CV方法和本文方法对上述三套条纹图进行了相位重建。由于实际原因，参考相位面很难得到，对此本文采用AIA算法的结果作为参考值，用于计算三种方法重建相位的误差。应当说明，AIA算法是一种高精度的多帧方法，其性能优于两帧算法，因此，可以为测试本文方法提供参考值。

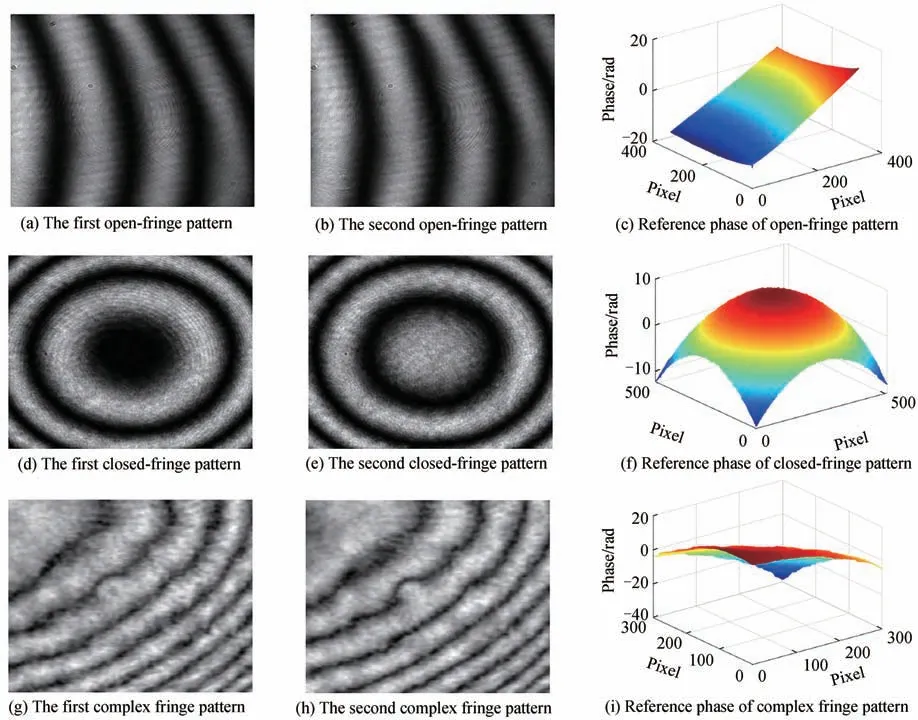
图 5 实验条纹图与参考相位Fig.5 The experimental interferograms and reference phase

为了获得参考相位，本文首先采用AIA算法，使用7帧相移条纹图分别解调了上述三套条纹图的相位，并将其视为各自的参考相位。图5分别给出了三套条纹图的前两帧条纹图以及得到的三个参考相位。

为了说明本文方法的效率，记录了三种方法的处理时间。表3给出了分别使用三种方法解调开形条纹图、闭形条纹图和复杂条纹图的耗时。可见，本文方法相比PCA&LSI方法和CV方法在处理实际条纹图时耗时最少，与仿真结果一致。

表3 处理时间（秒）Table 3 Processing time （s）

图6、图7和图8分别给出了使用三种不同方法处理开形条纹图、闭形条纹图和复杂条纹图的实验结果。分析开形条纹图的处理结果可知，由于此时相位面变化比较平缓，三种方法都成功实现了开形条纹图的相位重建，但本文方法的误差最小。在闭形条纹图处理实验中，特别在曲率较大的区域，CV法的结果一致性最差，而PCA&LSI方法与本文方法相对取得了较好的效果，但在边缘区域，虽然三种方法均出现了部分跳变，但是本文方法的结果一致性最好。由图8可知，与参考面（见图5（i））相比，三种方法都成功的实现了不规则面的相位重建，但CV方法重建的相位面上有明显的跳变（见图8（c）），而PCA&LSI方法与本文方法重建的相位面没有跳变。由复杂条纹图得到的重建相位误差分布可知，对于对比度差、条纹密度高、样品形状不规则的条纹图，本文方法相比其他两种方法仍取得了好的效果。另外，结合以上比较实验可知，三种方法的残差较为明显，这是因为二帧算法使用的信息较少，相比多帧算法，其抑制光强谐波、测量不确定性等误差的能力较差，因此提高条纹质量非常重要。

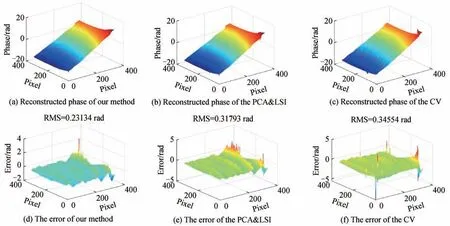
图 6 开形条纹图相位重建实验Fig.6 Experiment for the phase reconstruction using open interferogram

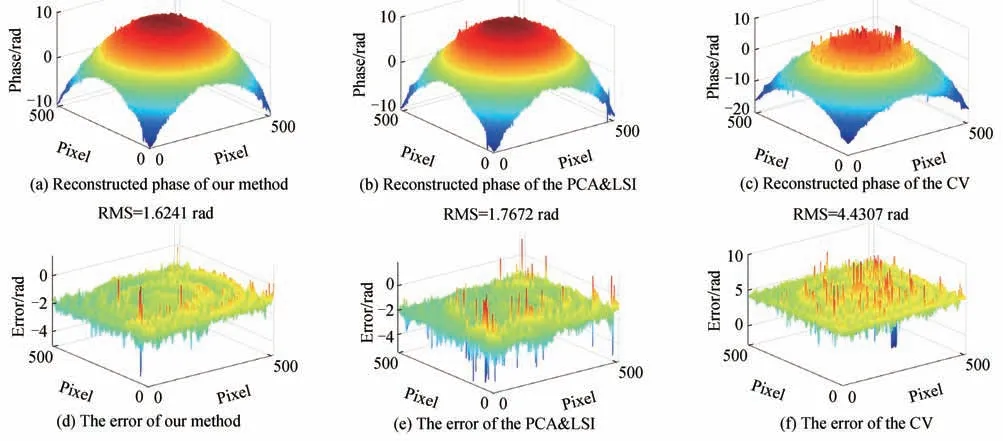
图 7 闭形条纹图相位重建实验Fig.7 Experiment for the phase reconstruction using closed interferogram

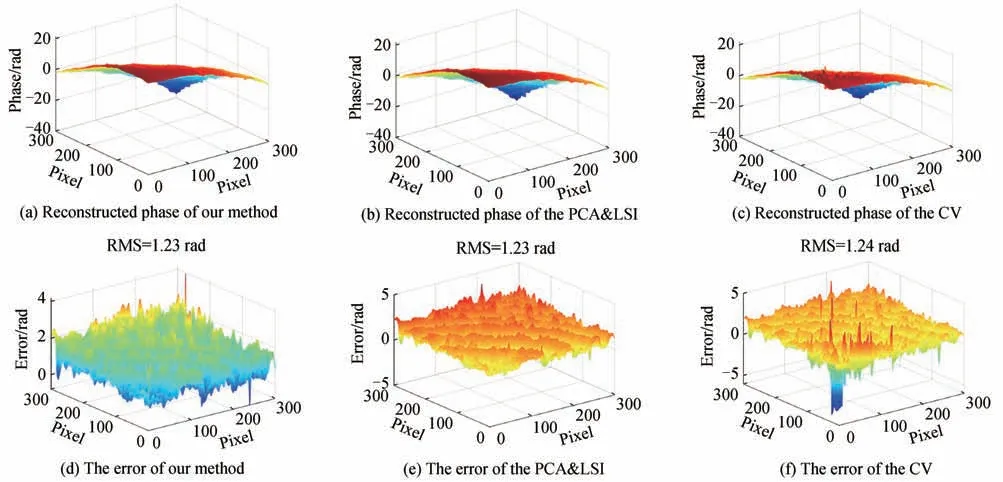
图 8 复杂条纹图相位重建实验Fig.8 Experiment for the phase reconstruction using the complex interferogram

从图6、图7和图8的误差分布图可以看出，本文方法测量结果明显优于PCA&LSI方法和CV方法，其重建误差相对于参考相位最小，而且耗时最短。因此可以证明，即使对于含有多个误差源的实际条纹图，如强度谐波、非均匀相移分布和随机加性强度噪声等，本文方法仍表现出了好的综合性能。

应当指出，本质上本文方法和PCA&LSI方法都是基于迭代细化的策略，区别在于本文方法提供的初值为相移，而PCA&LSI方法提供的初值为相位。本文方法的精度优于PCA&LSI方法的原因是，本文方法由于提供了一个较好的初值，相对于PCA&LSI方法可以更好促使迭代算法稳定地收敛于精确值。另外，PCA&LSI方法在应用中假定相移条纹图背景和振幅是时域变化的，该假定使得解调过程计算复杂，而且不能提高求解精度。而本文方法认为相移条纹图背景和振幅在时域是不变的，计算简单，且具有较快的处理速度。从本文仿真和实验的分析来看，将条纹图模型建模为背景和振幅时域变化是没必要的。再者实际测量时，相移量通常很小，由于背景和振幅的时域变化产生的误差相对其他误差而言可以忽略，因此，这种时域变化的复杂模型不能达到预期的提高精度的目的，反而影响了其精度。

4 结论

本文将AIA算法推广至二帧条纹图解调场合，提出了一种高精度的无需预滤波的两帧随机相移提取算法。首先在近似正交条件下估计相移，然后利用最小二乘迭代技术对处理结果进行细化，进而更新背景，促使处理结果不断逼近精确相位。由于本文方法使用了条纹图子图估计相移，与现有的相位重建方法相比，有较快的处理速度。另外，本文方法由于提供了一个较好的初值，具有可靠的收敛性。仿真及实验证明了本文方法精度高、速度快、可靠性好，是一种实用的两帧相移算法，并优于现有的典型两帧相移算法。