离心泵仿生微结构叶片减阻特性的仿真研究

黄明吉，刘圣艳，乔小溪，陈平，刘中海，张晓昊

摩擦磨损与润滑

离心泵仿生微结构叶片减阻特性的仿真研究

黄明吉1，刘圣艳1，乔小溪1，陈平1，刘中海2，张晓昊3

（1.北京科技大学 机械工程学院，北京 100083；2.长沙迪沃机械科技有限公司，长沙 410205；3.清华大学天津高端装备研究院，天津 300300）

通过在离心泵叶片表面布置仿生微结构实现离心泵的减阻，并获得仿生微结构的最优化设计参数。研究利用仿真模拟的方法，采用离心泵的扭矩变化对其减阻性能进行表征，考虑了仿生微结构的形态、截面形状和特征高度等结构参数的影响规律，通过分析叶片表面的湍流动能、剪切应力和近壁面层的速度云图揭示仿生微结构对离心泵减阻特性的影响机理。在3种微结构形态中，流向沟槽的减阻效果最好；在3种截面形状的微结构中，矩形截面的减阻效果最好；离心泵减阻率并非随微结构特征尺寸单调变化，而是存在最优值；所有微结构的减阻率均随着流量的增加而增加。当叶片表面布置流向、矩形沟槽时离心泵具有最优的减阻效果，且在全流量工况范围流向矩形沟槽结构的最大减阻率为8.39%。叶片表面微结构的布置可以实现离心泵减阻，其减阻机理与近壁面流体流动行为有关。表面微结构可有效降低叶片壁面的速度梯度，使速度沿壁面法线方向过渡更加均匀，且微结构内部低速流体层可有效控制和减弱近壁面区的湍动程度，减少湍流动能损耗；同时微沟槽内的反向涡流具有类“滚动轴承”作用，将滑动摩擦转换为滚动摩擦，降低摩擦阻力。

离心泵；仿生微结构；减阻；湍流动能；数值模拟

我国是世界上最大的煤炭生产国和消费国[1-2]，煤炭的开发和利用推动国民经济的发展，但煤矿矿床的水文地质条件较为复杂，矿井水灾的发生不仅影响正常生产，还会威胁工人人身安全，泵作为一种排水设备在处理煤矿透水事故中发挥着积极作用。然而泵的耗电量很大[3]，能源利用效率较低，泵在运行过程中存在机械损失以及摩擦和冲击等引起的水力损失，其中流体流经叶轮等过流部件时，由于摩擦引起的水力损失尤为严重[4-5]。降低离心泵内流体运动阻力，不仅可节约能源、提高泵运行的稳定性，也可降低流动诱导的噪声。因此，离心泵减阻特性的研究极其重要。

根据是否需要外部辅助设备和额外能量的输入，减阻可分为主动控制减阻和被动控制减阻。被动控制减阻方法由于成本较低，符合节能的目标，在实际应用中更广泛[6-8]，主要包括疏水表面减阻、聚合物添加剂减阻、柔性壁面减阻和非光滑表面减阻等，其中非光滑表面被认为是被动减阻中最具有潜力的方法。非光滑表面减阻法是受自然界生物的启发[8-16]，例如荷叶、鲨鱼皮表面[8-12]等，通过在流道壁面加工肋条、沟槽、凹坑或者凸起等仿生微结构，来改变近壁面流动状态，重塑湍流边界层拟序结构，从而实现减阻的目的。研究发现，鲨鱼在水中快速游动与其多结构的皮肤密切关系，其皮肤表面具有沿着流向的类沟槽有序排列的微小结构，即肤齿。早在1982年，Walsh等[8]首次发表了将鲨鱼表皮的微结构简化为不同形状沟槽进行减阻的试验研究，结果表明，沟槽结构能有效地降低壁面摩擦阻力，且减阻效果与沟槽的尺寸和形状密切相关。

宋保维等[17]数值模拟研究了棋盘状微结构疏水表面在湍流状态下的减阻特性，结果显示，在低雷诺数下，微结构内气体封存状态良好，减阻率最高约为30%。李山等[18]对光滑壁面和沟槽壁面的湍流边界层流场通过TR-PIV技术进行了试验测量，结果发现，沟槽降低了壁面摩擦阻力，并且正弦波沟槽的减阻率更大。受鲨鱼表皮微沟槽结构启发，Martin等[19]研究了刀刃形、锯齿形和扇贝形3种形状肋条对流场中平均阻力变化和涡旋结构的影响，结果表明，刀刃形的最大减阻可达11.6%。Chen等[20]仿真研究了航空发动机叶片表面布置微结构的形状的影响，结果显示，微结构叶片表面可明显降低压力损失，且三角形织构叶片表面的压力损失较小。Mele等[21]通过CFD仿真研究了肋条结构对涡轮螺旋桨飞机周围的气流动力学的影响，结果显示，在巡航状态下，肋条结构的布置可实现阻力降低13%。

对于表面仿生微结构的减阻机理，目前主要存在“第二涡群”、“突出高度”和“微型空气轴承”等3种理论。“第二涡群”理论认为反向旋转的流向涡与沟槽尖顶区域相互作用可产生小的二次涡，沟槽表面的小肋尖峰能够加速和增强“第二涡群”的发展，使得低速条带向外猝发随机涡的几率减小且程度减弱，使边界层附近的动量交换减弱，边界层流体稳定性提高，进而使近壁面边界层附近黏性阻力降低。“突出高度”理论认为在“突出高度”以下沟槽内的流动，绝大部分为黏性所阻滞，相当于增加了黏性底层的有效厚度[22]，降低了壁面平均速度梯度，从而减小了表面摩擦阻力。潘家正从边界层涡结构的观点出发，提出了边界层底部“微型空气轴承”的概念。沟槽内形成的“小涡”被沟槽挡住后，滞留在微小沟槽内部，充当微型空气轴承[23]，把空气与运动物体的滑动摩擦转变为滚动摩擦，从而实现减阻效果。

非光滑表面减阻技术在流体减阻应用中具有广阔的发展前景，然而将非光滑表面减阻技术应用到复杂旋转流体机械离心泵中的研究还比较缺乏。本文以高转速、高扬程离心泵为研究对象，将表面微结构引入到离心泵叶轮叶片表面，通过数值模拟方法，研究不同形态、形状及尺寸的微结构对泵的减阻性能的影响规律，为泵的减阻设计提供理论指导。

2 数值模拟

2.1 几何模型

离心泵的基本设计参数：流量=240 m3/h，扬程=120 m，转速=3 600 r/min，叶轮进口圆环截面的外圆直径j=132 mm，内圆直径为h=60 mm，叶轮出口直径2=258 mm，叶片数=6。利用CFturbo软件建立如图1a所示的离心泵流场计算域模型（未显示进出水管部分）。离心泵过流部件主要包括叶轮、蜗壳、进水管和出水管4个部分。为了避免进出口效应的影响，更准确地模拟离心泵的内部流场，几何模型设置进水管的长度为叶轮进口直径的3倍（198 mm），出水管的长度为蜗壳出口直径的6倍（630 mm）。

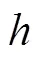
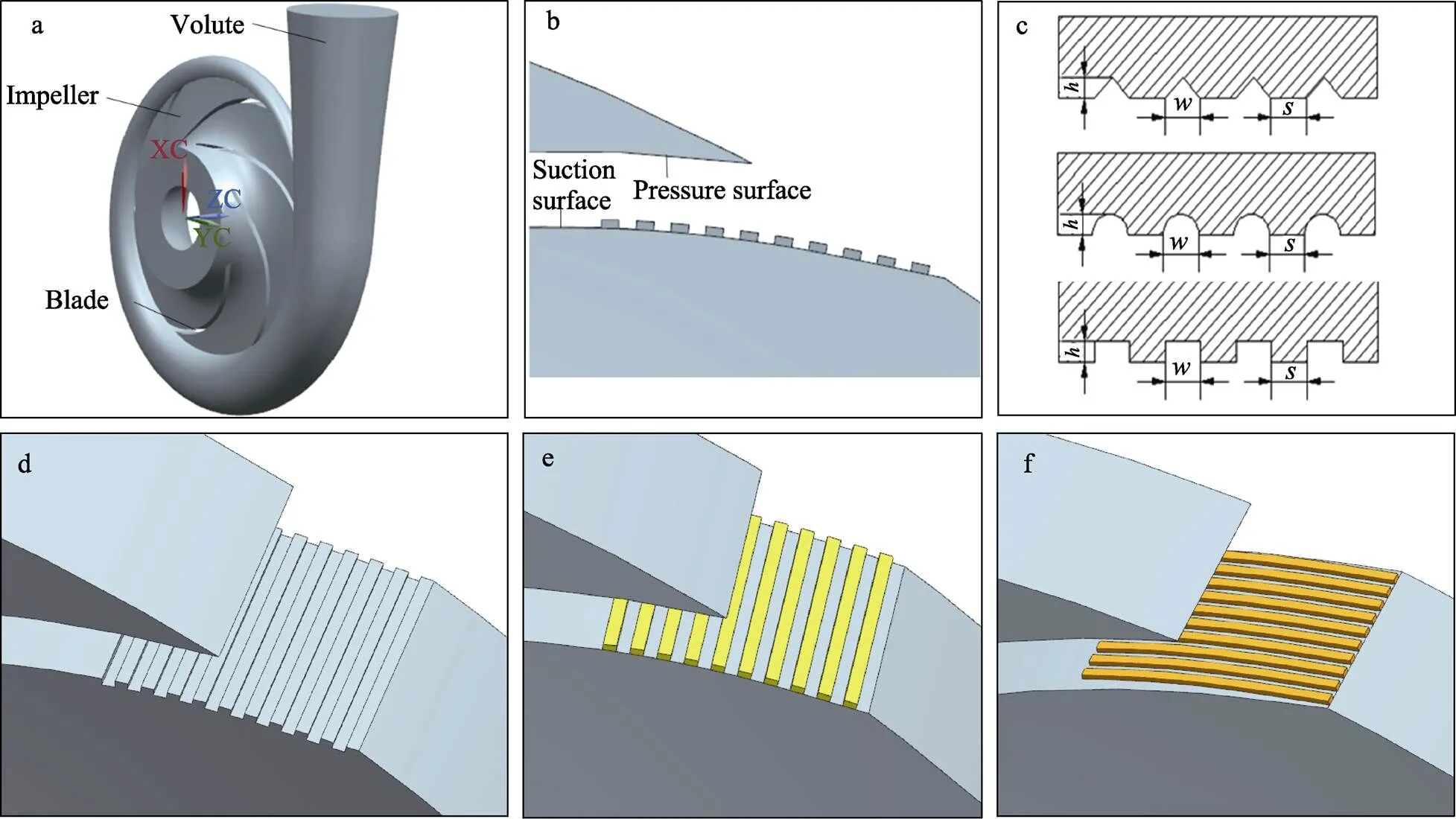
图1 离心泵计算域模型（a），微结构布置位置（b）和形状（c），以及横向肋条（d）、横向沟槽（e）和流向沟槽（f）3种形态

2.2 网格划分及无关化验证

离心泵过流部件为复杂的三维曲面，叶轮和蜗壳选择四面体非结构网格，进水管和出水管为圆柱体结构，选择六面体结构网格，并对叶片表面微结构处的网格进行局部细化加密，具体叶轮流体域的网格划分如图2a所示。为保证仿真计算的效率和准确性，对光滑模型泵进行网格无关性验证，本文选定5组不同的网格数量，并监测其对泵的扬程和效率变化，结果如图2b所示。结果显示，泵的扬程随网格数的增加在一定范围内小幅度波动，且与理论设计值120 m的相对误差均在1%以内；泵的效率随网格数量的增加而逐渐增加，当网格数达到100万后，效率趋于稳定值，并接近理论计算效率的76%。因此在本文的数值计算中，选择离心泵模型的网格数量约为100万。

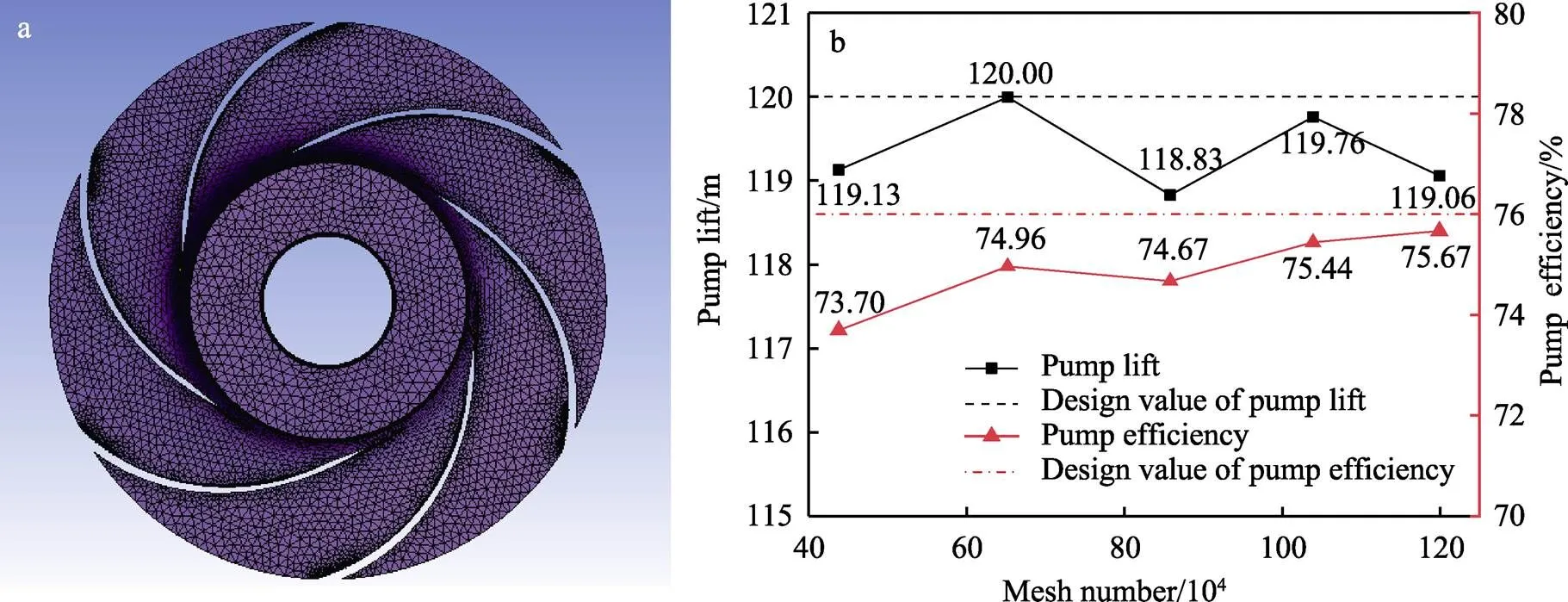
图2 叶轮流体域网格划分（a）和无关化验证（b）

2.3 湍流模型和边界条件

离心泵内部流体为复杂的三维湍流流动[25]，存在不同程度的回流、漩涡和脱流等现象，因此仿真采用适应性更强的RNG-湍流模型。该模型考虑了平均流动中的旋转效应，在强旋流动的计算中具有较高的精度，能够同时满足高计算精度和短计算时间的要求。同时壁面函数设置为标准壁面函数（Standard Wall Functions），叶片表面未考虑壁面粗糙度的影响。

离心泵计算域包括旋转域和静止域，其中叶轮为旋转域，叶轮转速为3 600 r/min，绕轴旋转方向由右手定则确定，叶轮前后盖板及叶片与流体接触面设置为旋转壁面。进口段、蜗壳和出水段为静止域，进出口壁面及蜗壳壁面设置为静止壁面。

2.4 性能表征参数

离心泵通过旋转轴来驱动叶轮，流体从叶轮流入后沿叶片轮廓流向出口。在内部流动时，叶片表面受到的阻力有近壁面区域的摩擦阻力和前后壁面引起的压差阻力，综合考虑2种阻力因素的影响，最终以叶轮的扭矩表现出来。因此，本文将叶轮所受扭矩的变化作为仿生微结构叶片减阻效果的评价指标，其减阻率计算公式为：

表1 入口边界参数

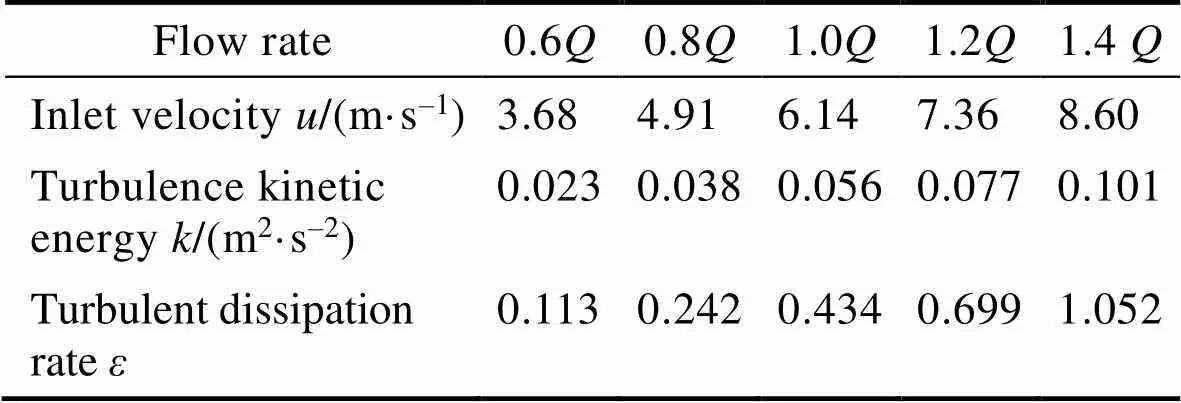
Tab.1 The inlet boundary conditions

3 结果与讨论

3.1 仿生微结构形态和截面形状的影响

首先研究了不同流量工况下，横向沟槽、横向肋条和流向沟槽3种微结构形态，以及三角形、半圆形和矩形3种微结构截面形状对离心泵减阻性能的影响规律。其中微结构的特征宽度为1.0 mm，特征高度为0.5 mm，相邻微结构的间距均为1 mm，具体仿真参数如表2所示，仿真结果如图3和图4所示。

由图3结果可知，针对不同截面形状的微结构，在叶片表面布置流向沟槽的减阻率最高，其次为横向沟槽，横向肋条的减阻率最低。同时，针对不同形态、截面形状微结构叶片，离心泵的减阻效果随着流量的增加而逐渐增加。叶片设置有流向沟槽的离心泵在全工况范围内均显示出减阻效果，当流量为1.0时，矩形流向沟槽结构的离心泵的减阻率最大达3.7%。在全工况范围来看，在叶片表面布置矩形流向沟槽结构时的减阻率最大为8.39%；而横向沟槽和横向肋条结构，在小流量时甚至表现为增阻效果，仅在大流量范围内才具有减阻作用，但横向矩形沟槽在全工况范围内均表现为减阻效果。

表2 仿生微结构形态和形状影响研究模型的参数

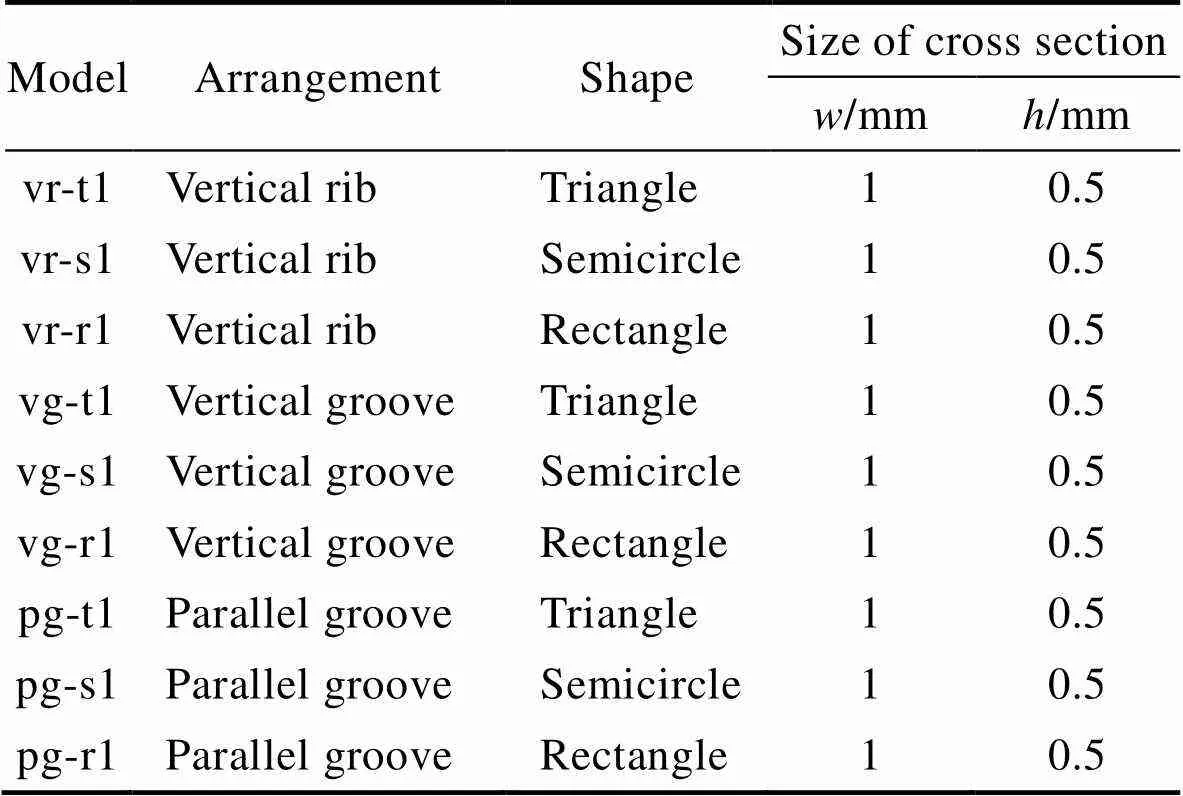
Tab.2 Bionic microstructures with different arrangements and shapes

根据图3结果可知，横向沟槽和流向沟槽具有较好的减阻效果，因此进一步将图3的数据进行处理，得到了横向沟槽和流向沟槽2种微结构形态下，微结构形状对减阻特性的影响规律，如图4所示。结果显示，在全工况范围，在叶片表面布置矩形微结构时减阻效果最好，三角形微结构次之，半圆形微结构的减阻效果相对较差；针对流向沟槽微结构，3种形状的微结构均可在全工况范围内实现减阻，且微结构的形状对减阻率的影响程度随流量的增加而增加；针对横向沟槽，三角形和半圆形在较小流量0.6时为增阻，其余流量情况均为减阻，且减阻率随流量的增加而增加。

综上所述，针对所研究的微结构形状和形态，不同形状的流向沟槽在全流量工况范围内均有一定的减阻效果，且流向矩形沟槽具有最好的减阻率；横向肋条微结构的减阻效果最差，甚至在小流量范围工作时表现出增阻效果。

图3 三角形（a）、半圆形（b）、矩形（c）3种截面形状下微结构形态对离心泵减阻率的影响

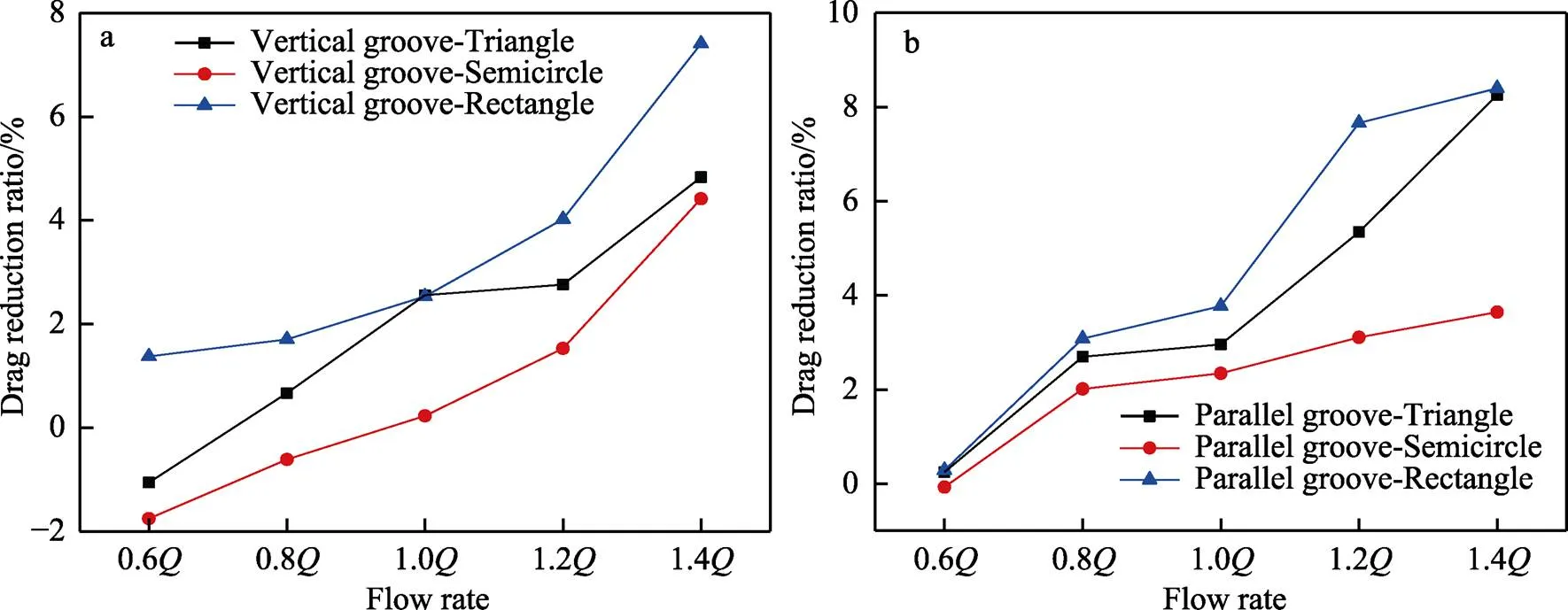
图4 横向沟槽（a）和流向沟槽（b）2种形态下微结构形状对离心泵减阻率的影响

离心泵运行过程中，叶轮叶片等过流表面所受到的阻力主要包括摩擦阻力和压差阻力，其中摩擦阻力是由黏性剪切应力和湍流雷诺应力两部分组成，湍流雷诺应力是由于流速脉动引起质点间的动量交换产生的附加应力，可用湍流动能来反映湍流雷诺应力。为进一步揭示微结构形态、形状对离心泵减阻影响的机理，本文分析了叶片表面的剪切应力（主要是由于摩擦阻力引起）、湍流动能和近壁面区域速度的云图，结果如图5—8所示。为方便分析，微结构叶片的表面剪切应力、湍流动能和近壁面区域速度云图的标尺与光滑叶片相同。

图6为额定流量下，微结构形状、形态对离心泵叶片表面剪切应力的影响。结果显示，叶片出口处布置表面微结构可以明显地降低该区域叶片表面的剪切应力，同时也明显影响了未布置微结构的叶片压力面的表面剪切应力。当微结构截面形状相同时，布置流向沟槽结构的叶片表面的最大剪切应力和高剪切应力分布区域均最小，布置横向沟槽结构的叶片表面次之。当微结构布置形态相同时，矩形微结构表面最大剪切应力和高剪切应力分布区域均最小，三角形微结构叶片表面次之。微结构的形状、形态对叶片表面剪切应力和离心泵减阻率的影响规律具有很好的一致性。

额定流量下，微结构形状和形态对离心泵叶片表面湍流动能的影响如图7所示。结果显示，高湍流动能出现在靠近叶片出口区域。当微结构截面形状相同时，布置流向沟槽结构的叶片表面的湍流动能值较小且高湍流动能分布区域减少，横向肋条叶片表面的湍流动能和高湍流动能区域均较大。当微结构形态相同时，矩形微结构表面湍流动能最小，三角形微结构次之，而半圆形沟槽表面湍流动能最大。同样，微结构的形状、形态对叶片表面湍流动能和离心泵减阻率的影响规律也具有很好的一致性。

综合图6和图7可以看出，当表面布置有流向矩形沟槽时，叶片表面的剪切应力和湍流动能均较小，因而具有较大减阻率。微结构对叶片表面湍流动能和剪切应力的影响，主要源于微结构对近壁面区域速度场的改变，如图8所示。当叶片表面布置横向肋条时，近壁面区域的流动紊乱程度明显高于横向沟槽表面，流向沟槽表面的湍流程度最小，这表明叶片表面布置流向微沟槽结构可使其附近的湍流程度得到较好控制，且叶片整体的湍动程度均有较为明显的控制和减弱，从而降低了叶轮内流体流动时产生的能量损耗，起到了减阻作用。同时，与流向肋条和横向沟槽结构相比，流向沟槽明显降低了近壁面层流体的速度梯度，具有较小的黏性摩擦阻力。针对3种形状的流向沟槽，其近壁面层的紊流程度和速度梯度均明显降低，因此均表现出减阻效果。

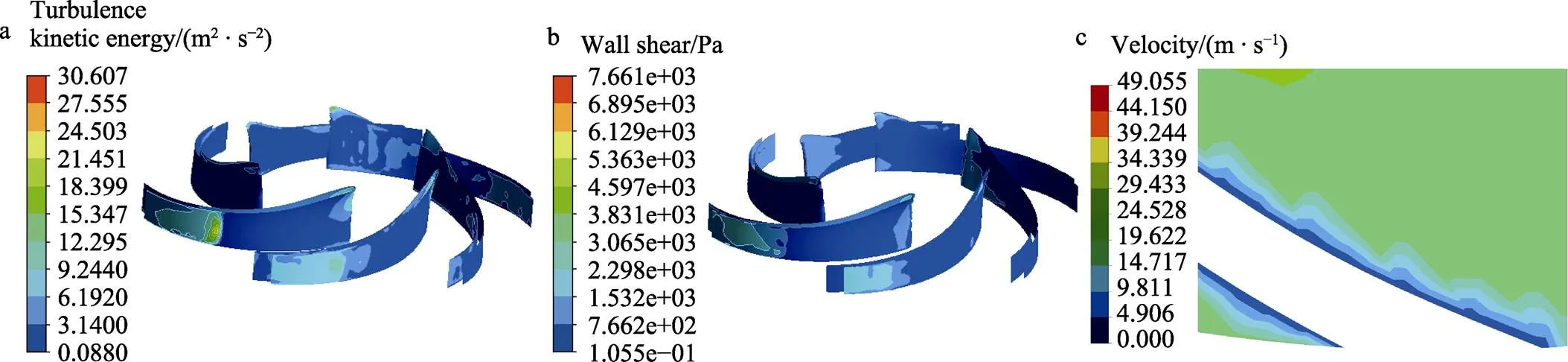
图5 光滑叶片的湍流动能（a）、剪切应力（b）和表面速度（c）云图

图6 额定流量下微结构形状、形态对壁面剪切应力云图的影响

图7 额定流量下微结构形状、形态对表面湍流动能云图的影响

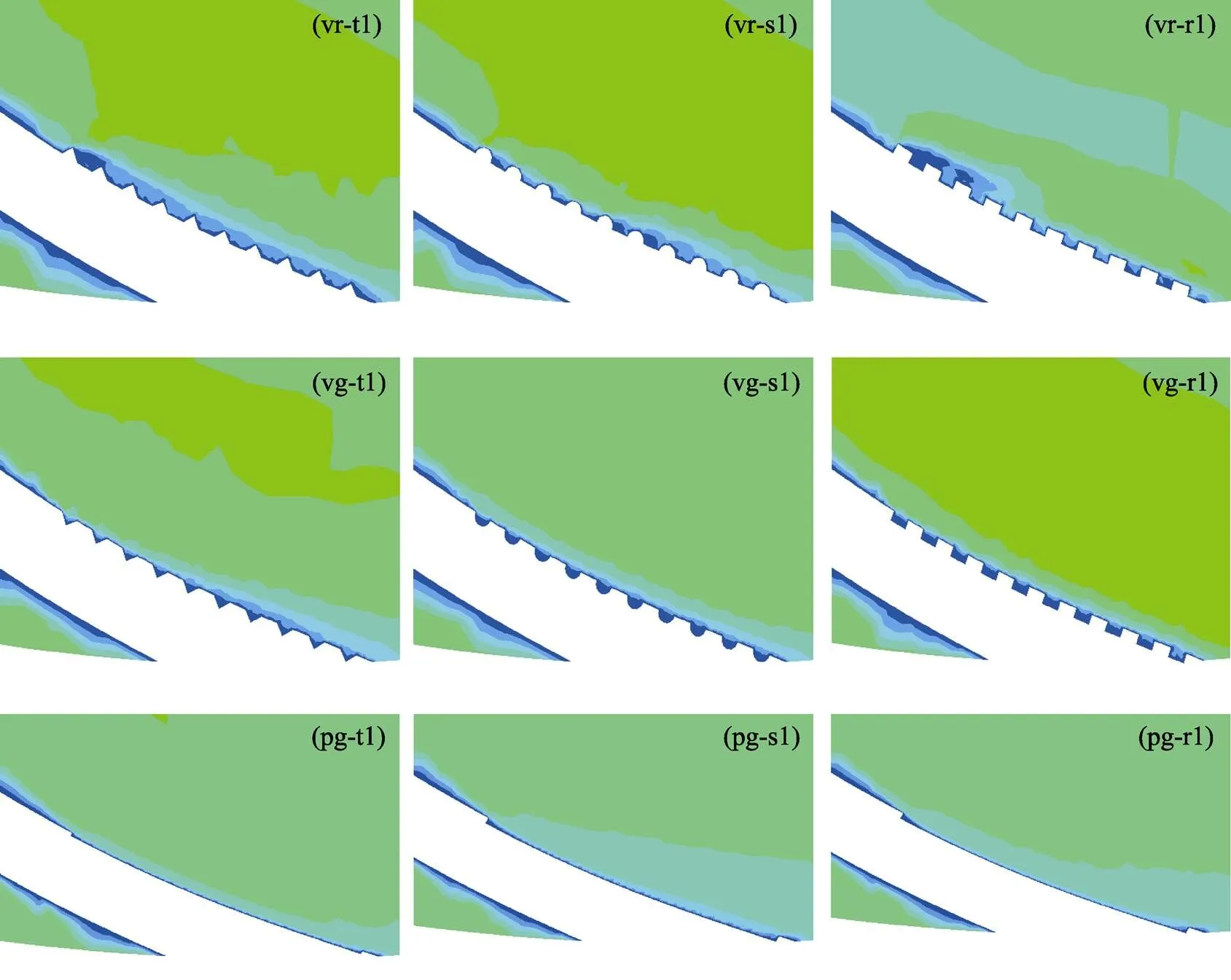
图8 额定流量下微结构形状、形态对叶片近壁面区速度云图的影响

额定流量时微结构叶片近壁面区域的迹线见图9，可知表面微结构会明显改变近壁面区域速度场的分布，矩形横向沟槽和肋条2种形态的微结构内部均产生了涡流结构。布置横向矩形沟槽的叶片表面，其近壁面区域内湍流的猝发明显降低且紊流层厚度减小，同时被限制在沟槽内的涡流一定程度起到“滚动轴承”的减阻作用，因此横向沟槽具有减阻效果。叶片表面布置横向矩形肋条导致微结构和流体作用初始区域湍流猝发情况加剧，使得近壁面紊流层的厚度增加，但在横向肋条与流体作用的下游，其与横向沟槽作用类似，具有一定的滚动减阻作用，因此在额定流量时横向矩形肋条减/增阻效果不明显。

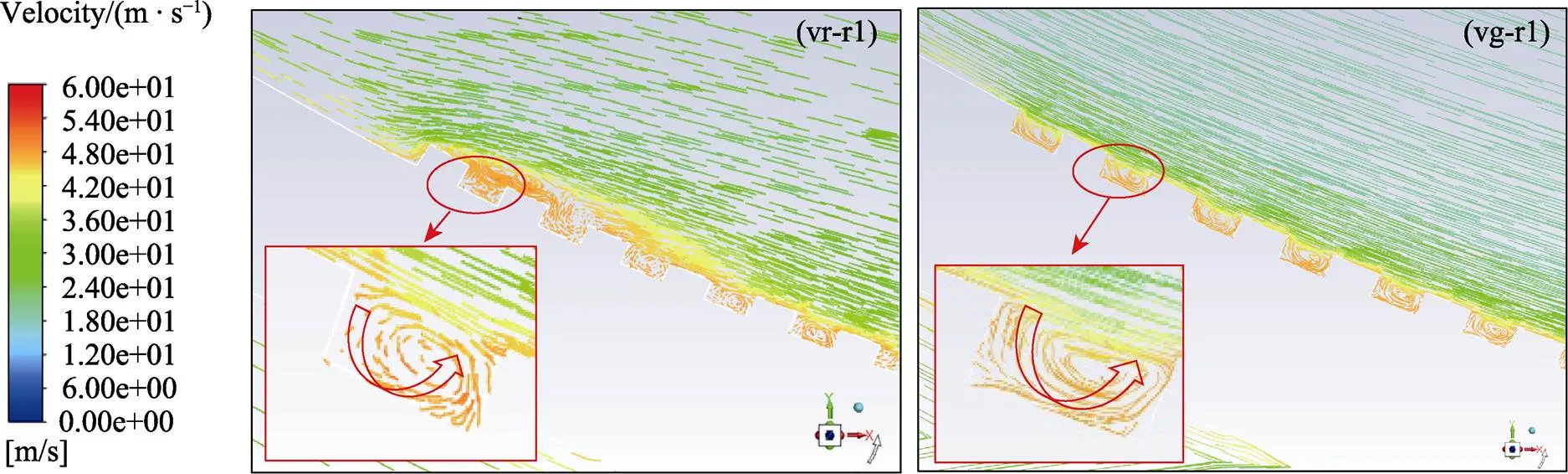
图9 矩形横向肋条（vr-r1）和沟槽（vg-r1）的迹线图

流体经过沟槽结构时，流体的流向会在尖角附近发生偏转，从而形成反向旋转的涡。由图10中3种截面形状的横向沟槽叶片近壁面区域的迹线图可以发现，3种微结构内部均形成了反向涡，根据“第二涡群”反向旋转的流向涡与沟槽尖顶区域相互作用可产生小的二次涡，减少低速条带向外猝发随机涡的几率和程度，即抑制了湍流的产生。不同微结构形状“二次涡”的位置不同，对叶片近壁面流场的影响程度不同。矩形沟槽有两个尖角，沟槽谷底间距最大，沟槽顶角为零，因此受到沟槽尖顶的阻碍而分离出的“二次涡”的位置最高，“二次涡”与沟槽边界的接触区域的面积最小，因此“二次涡”受沟槽尖顶的作用力最小，应力较高区域的面积最小；并且矩形沟槽底部层流的厚度最大，使得整个仿生微结构叶片表面的剪应力最低，因此在叶片表面布置矩形沟槽的减阻效果最好。

图10 3种微结构形状下横向沟槽的迹线图

3.2 仿生微结构尺寸的影响

由图3和图4可知，减阻效果位于前三的微结构为流向矩形沟槽结构、流向三角形沟槽结构、横向矩形沟槽结构，因此进一步选择这3种微结构以研究微结构尺寸对减阻特性的影响规律。仿真采用的仿生微结构参数见表3，结果如图11所示。

由图11可知，针对3种形式的微结构，当微沟槽高度为0.5 mm时，3组微结构的减阻效果均最好，其次是沟槽高度为0.75 mm的，沟槽高度为0.25 mm的减阻率最小。微结构高度尺寸对减阻率的影响程度随着流量的增加而增加。当叶片表面布置微流向矩形沟槽时，微结构的高度尺寸对其减阻率的影响程度较低。当表面布置微横向矩形沟槽时，微结构高度的影响程度较大。

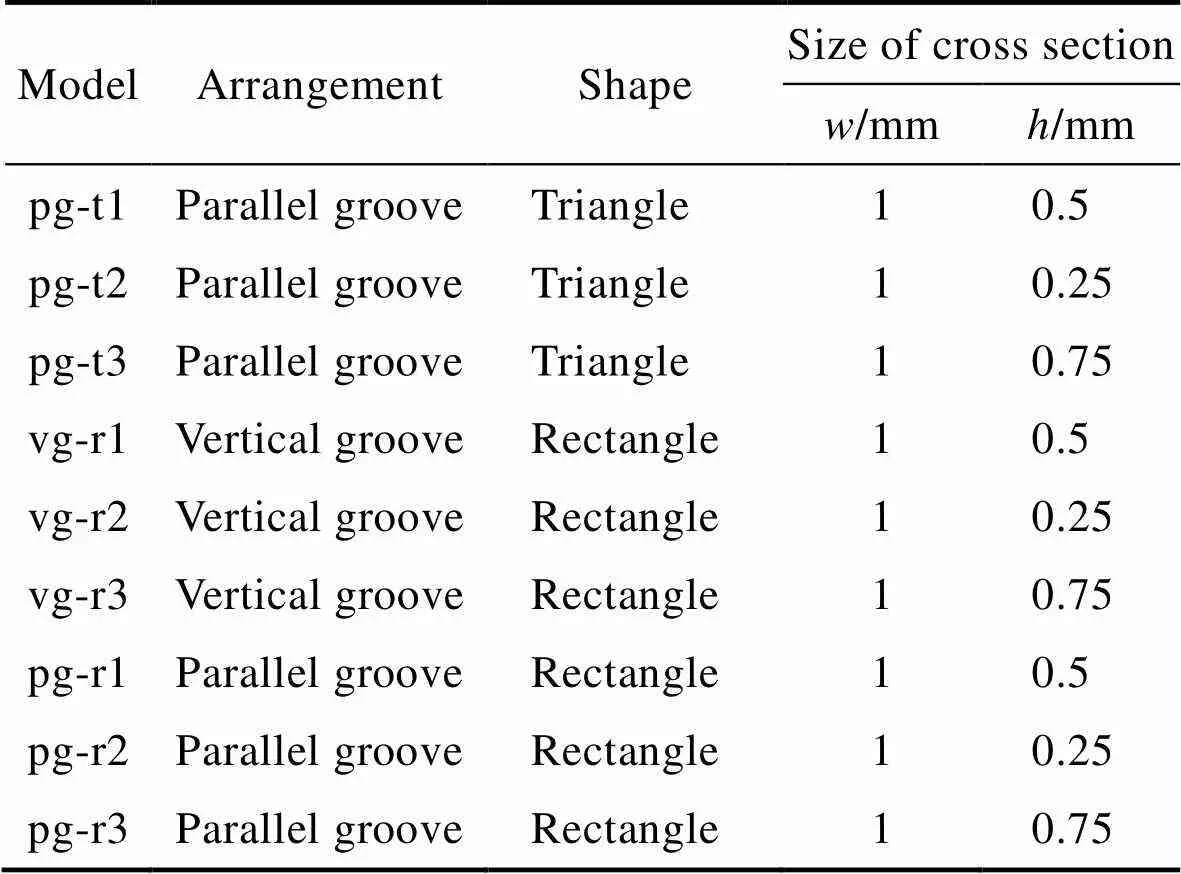
表3 微结构尺寸影响研究的模型参数

图11 横向矩形沟槽（a）、流向三角沟槽（b）和流向矩形沟槽（c）条件下微结构高度对离心泵减阻率的影响。

根据图11结果，进一步分析横向矩形沟槽的高度影响减阻效果的机理。沟槽尺寸对减阻率的影响与沟槽中的流动形态有关，图12给出了横向矩形沟槽3种高度时微结构内部的迹线图。结果显示，当微结构高度=0.25 mm时，由于沟槽的宽高比过大，在沟槽内部没有形成明显的流动涡，对近壁面区流动的抑制作用较弱，减阻率最小。当微结构高度为0.5、0.75 mm时，微沟槽内均形成了形态较好且稳定流动涡，但由于=0.75 mm的微沟槽内反向涡的中心距沟槽外平面距离较大，其对近壁面区域湍流的抑制效果减弱，且反向流的“滚动轴承”的减阻效果减弱，因此与=0.5 mm的矩形沟槽相比，减阻率降低。

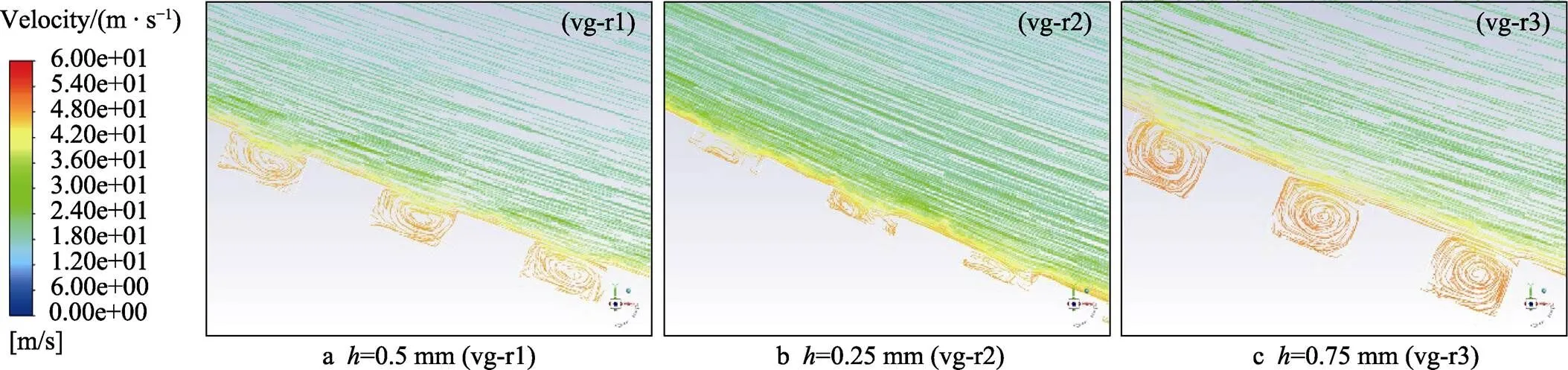
图12 3种高度下横向矩形沟槽的内部迹线图

4 结论

通过在离心泵叶片表面布置仿生微结构可以实现明显减阻，减阻率与布置微结构的形态、形状和尺寸等密切相关。本文通过在叶片出口处的吸力面上布置长度为叶片型线长度的13%微结构，研究分析了相关因素对离心泵减阻率的影响规律和机理。

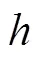
表面微结构的减阻与近壁面区域流体的流动行为相关，叶片表面仿生微结构的布置会对近壁面处的速度场和湍流强度产生影响，抑制了流场内由于速度梯度过大而导致小尺度涡的产生，并阻止了涡量的增大，使其附近的湍动程度得到较好控制，且全流场整体的湍动程度均有较明显的控制和减弱，从而降低了叶轮内流体流动时产生的能量损耗，降低运动阻力。同时微结构还可以改变近壁面层流体的速度梯度，降低表面摩擦阻力，且微结构内的反涡流结构还具有类“滚动轴承”的减阻效果。

[1] LI Wei, YOUNGER P L, CHENG Yuan-ping, et al. Addressing the CO2Emissions of the World's Largest Coal Producer and Consumer: Lessons from the Haishi­wan Coalfield, China[J]. Energy, 2015, 80: 400-413.

[2] SHI Xun-peng, WANG Ke, SHEN Yi-fan, et al. A Permit Trading Scheme for Facilitating Energy Transition: A Case Study of Coal Capacity Control in China[J]. Journal of Cleaner Production, 2020, 256: 120472.

[3] 田丽梅, 梅浩然, 李新红, 等. 基于仿生耦合功能表面的离心水泵增效机制研究[J]. 农业机械学报, 2015, 46(4): 65-69, 119.

TIAN Li-mei, MEI Hao-ran, LI Xin-hong, et al. Enhancement Mechanism Investigation of Centrifugal Pump Based on Bionic Coupling Functional Surface[J]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(4): 65-69, 119.

[4] 裴吉, 王文杰, 袁寿其, 等. 低比转数离心泵内部非定常流动特性数值预测[J]. 农业机械学报, 2014, 45(1): 79-83, 88.

PEI Ji, WANG Wen-jie, YUAN Shou-qi, et al. Numerical Prediction of Inner Flow Unsteadiness in a Low-Specific Speed Centrifugal Pump[J]. Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(1): 79-83, 88.

[5] HOU Hu-can, ZHANG Yong-xue, LI Zhen-lin, et al. Numerical Analysis of Entropy Production on a LNG Cryogenic Submerged Pump[J]. Journal of Natural Gas Science and Engineering, 2016, 36: 87-96.

[6] ABDULBARI H A, MAHAMMED H D, HASSAN Z B Y. Bio-Inspired Passive Drag Reduction Techniques: A Review[J]. Chem Bio Eng Reviews, 2015, 2(3): 185-203.

[7] 秦立果, 杨浩, 董光能, 等. 柔性表面织构化在海洋装备减阻与防污上的应用[J]. 表面技术, 2019, 48(6): 150-157.

QIN Li-guo, YANG Hao, DONG Guang-neng, et al. Application of Textured Surface Flexible Materials in Drag Reduction and Antifouling of Marine Equipment[J]. Surface Technology, 2019, 48(6): 150-157.

[8] WALSH M. Turbulent Boundary Layer Drag Reduction Using Riblets[C]//20th Aerospace Sciences Meeting. Orlando: AIAA, 1982: 169.

[9] DEAN B, BHUSHAN B. Shark-Skin Surfaces for Fluid-Drag Reduction in Turbulent Flow: A Review[J]. Philosophical Transactions Series A, Mathematical, Physical, and Engineering Sciences, 2010, 368(1929): 4775-4806.

[10] YANG Shao-qiong, LI Shan, TIAN Hai-ping, et al. Tomo­graphic PIV Investigation on Coherent Vortex Structures over Shark-Skin-Inspired Drag-Reducing Riblets[J]. Acta Mechanica Sinica, 2016, 32(2): 284-294.

[11] FU Y F, YUAN C Q, BAI X Q. Marine Drag Reduction of Shark Skin Inspired Riblet Surfaces[J]. Biosurface and Biotribology, 2017, 3(1): 11-24.

[12] BIXLER G D, BHUSHAN B. Fluid Drag Reduction with Shark-Skin Riblet Inspired Microstructured Surfaces[J]. Advanced Functional Materials, 2013, 23(36): 4507-4528.

[13] GU Yun-qing, ZHAO Gang, ZHENG Jin-xing, et al. Experi­mental and Numerical Investigation on Drag Reduction of Non-Smooth Bionic Jet Surface[J]. Ocean Engineering, 2014, 81: 50-57.

[14] QIAO Xiao-xi, ZHANG Xiang-jun, CHEN Ping, et al. Effects of Square Micro-Pillar Array Porosity on the Liquid Motion of near Surface Layer[J]. Chinese Physics B, 2020, 29(2): 024702.

[15] SONG Xiao-wen, LIN Peng-zhe, LIU Rui, et al. Skin Friction Reduction Characteristics of Variable Ovoid Non-Smooth Surfaces[J]. Journal of Zhejiang University- Science A, 2017, 18(1): 59-66.

[16] TIAN Li-mei, JIN E, LI Zi-yuan, et al. The Fluid Control Mechanism of Bionic Structural Heterogeneous Com­posite Materials and Its Potential Application in Enhan­cing Pump Efficiency[J]. Advances in Mechanical En­gineering, 2015, 7(11): 168781401561955.

[17] 宋保维, 任峰, 胡海豹, 等. 表面张力对疏水微结构表面减阻的影响[J]. 物理学报, 2014, 63(5): 054708.

SONG Bao-wei, REN Feng, HU Hai-bao, et al. Drag Reduction on Micro-Structured Hydrophobic Surfaces Due to Surface Tension Effect[J]. Acta Physica Sinica, 2014, 63(5): 054708.

[18] 李山, 姜楠, 杨绍琼. 正弦波沟槽对湍流边界层相干结构影响的TR-PIV实验研究[J]. 物理学报, 2019, 68(7): 074702.

LI Shan, JIANG Nan, YANG Shao-qiong. Influence of Sinusoidal Riblets on the Coherent Structures in Tur­bulent Boundary Layer Studied by Time-Resolved Particle Image Velocimetry[J]. Acta Physica Sinica, 2019, 68(7): 074702.

[19] MARTIN S, BHUSHAN B. Modeling and Optimization of Shark-Inspired Riblet Geometries for Low Drag Applications[J]. Journal of Colloid and Interface Science, 2016, 474: 206-215.

[20] ZHANG Chen, SAURAV BIJAY K. Investigation on Drag Reduction Performance of Aero Engine Blade with Micro-Texture[J]. Aerospace Science and Technology, 2018, 72: 380-396.

[21] MELE B, RUSSO L, TOGNACCINI R. Drag Bookkeeping on an Aircraft with Riblets and NLF Control[J]. Aerospace Science and Technology, 2020, 98: 105714.

[22] 李芳, 赵刚, 刘维新, 等. 仿生射流孔形状减阻性能数值模拟及实验研究[J]. 物理学报, 2015, 64(3): 034703.

LI Fang, ZHAO Gang, LIU Wei-xin, et al. Numerical Simulation and Experimental Study on Drag Reduction Performance of Bionic Jet Hole Shape[J]. Acta Physica Sinica, 2015, 64(3): 034703.

[23] 王晓娜, 耿兴国, 臧渡洋. 一维周期与准周期排列沟槽结构的流体减阻特性研究[J]. 物理学报, 2013, 62(5): 054701.

WANG Xiao-na, GENG Xing-guo, ZANG Du-yang. Drag-Reduction of One-Dimensional Period and Puasiperiod Groove Structures[J]. Acta Physica Sinica, 2013, 62(5): 054701.

[24] 牟介刚, 代东顺, 谷云庆, 等. 非光滑表面离心泵叶轮的流动减阻特性[J]. 上海交通大学学报, 2016, 50(2): 306-312.

MOU Jie-gang, DAI Dong-shun, GU Yun-qing, et al. Characteristics of Non-Smooth Surface Drag Reduction Influence on Centrifugal Pump Impeller[J]. Journal of Shanghai Jiao Tong University, 2016, 50(2): 306-312.

[25] SHI Bao-cheng, WEI Jin-jia. Numerical Simulation of 3D Solid-Liquid Turbulent Flow in a Low Specific Speed Centrifugal Pump: Flow Field Analysis[J]. Advances in Mechanical Engineering, 2014, 6: 814108.

Simulation Study on the Drag Reduction of Centrifugal Pump with Bionic Micro-structured Blade

1,1,1,1,2,3

(1. School of Mechanical Engineering, University of Science and Technology Beijing, Beijing 100083, China; 2. Dewater Technology, Changsha 410205, China; 3. Tianjin Research Institute for Advanced Equipment, Tsinghua University, Tianjin 300300, China)

Centrifugal pump plays an important role in dealing with the water flooding accident in a coal mine. However, it has disadvantages of high mechanical loss and low energy utilization efficiency. Thus, studying the drag reduction performance of a centrifugal pump is essential. Not only it can save energy, but also can improve the pump stability. Here the drag reduction of the centrifugal pump is realized by arranging bionic microstructures on the centrifugal pump blade surfaces, and the optimal design parameters are obtained. In the paper, the influence rules and mechanisms of the bionic microstructures on the drag reduction of the pump are investigated by simulation method, and the variations in the impeller working torques caused by the bionic microstructures, compared to that of the pump with smooth blade surfaces, are used to characterize the drag reduction ratio. The effects of the arrangement, shape, and height size of the bionic microstructures are considered. And the microstructures are arranged on the outlet of the blade suction surfaces with an area ratio of 13%.

Results show that in the three arrangements of vertical rib, vertical groove, and parallel groove, the parallel groove has the highest drag reduction ratio. And for all the flow rates analyzed, all the parallel grooves with different cross-section shapes can realize drag reduction. In the three shapes of triangle, semicircle, and rectangle, the rectangular shape has the best drag reduction performance. The drag reduction ratio does not change monotonically with the microstructure height increasing. For the three heights analyzed, all the three kinds of microstructures with=0.5 mm have the largest drag reduction ratio. For all bionic micro-structured surfaces, their drag reduction ratios increase with the flow rate increasing. For all conditions, the blade surface with a parallel rectangular groove has the highest drag reduction percentage of 8.39%.

The bionic microstructures arranged on the blade surface will inevitably influence the flowing behaviors, especially for the near-surface fluid layer. The flow resistances are mainly caused by the frictional resistance and the differential pressure resistance. The friction resistance is composed of the viscous shear stress and the turbulent Reynolds stress, which are closely related to the flowing behaviors. In the paper, the path line figure near the blade surface, as well as the nephogram of velocity, turbulence kinetic energy, and shear stress are used to analyze the influence rules and mechanisms. The low-speed fluid layer trapped in the microstructures can effectively control and weaken the turbulence of the near-surface fluid layer, thus reducing the turbulent kinetic energy loss. Meanwhile, there are obvious reverse flow vortices in the microgrooves as shown in the path line figure. The reverse flow vortex can work as a "rolling bearing", which transforms the sliding friction into the rolling friction, thus reducing the fluid friction resistance. The low-speed fluid layer trapped in the microstructures can also increase the effective thickness of the boundary viscous layer and decrease the velocity gradient of the near-surface layer, resulting in lower surface frictional resistance. This research provides theoretical guidance for reducing energy loss of the centrifugal pump by using the bionic microstructure surface.

centrifugal pump; bionic microstructure; drag reduction; turbulence kinetic energy; numerical simulation

TH117

A

1001-3660(2023)02-0196-10

10.16490/j.cnki.issn.1001-3660.2023.02.017

2022–04–13；

2022–10–22

2022-04-13；

2022-10-22

国家重点研发计划（2018YFC0810500）；国家自然科学基金（51975042、51905032）；中央高校基本业务费（FRF-TP-19-004A3）

The State Key Development Program for Basic Research of China (2018YFC0810500); the National Natural Science Foundation of China (51975042, 51905032); the Fundamental Research Funds for the Central Universities, China (FRF-TP-19-004A3)

黄明吉（1972—），男，博士，副教授，主要研究方向为智能制造与装备智能技术。

HUANG Ming-ji (1972-), Male, Doctor, Associate professor, Research focus: intelligent manufacturing and equipment intelligent technology.

乔小溪（1986—），女，博士，副教授，主要研究方向为机械表面界面科学和摩擦学。

QIAO Xiao-xi (1986-), Female, Doctor, Associate professor, Research focus: surface and interface science in machinery, tribology.

黄明吉, 刘圣艳, 乔小溪, 等.离心泵仿生微结构叶片减阻特性的仿真研究[J]. 表面技术, 2023, 52(2): 196-205.

HUANG Ming-ji, LIU Sheng-yan, QIAO Xiao-xi, et al. Simulation Study on the Drag Reduction of Centrifugal Pump with Bionic Micro- structured Blade[J]. Surface Technology, 2023, 52(2): 196-205.

责任编辑：万长清