利用劳条件求取双相位光栅干涉仪灵敏度

杨君，黄建衡，单雨征，雷耀虎，宗方轲，郭金川

（深圳大学 物理与光电工程学院 光电子器件与系统教育部/广东省重点实验室，深圳 518060）

0 引言

在过去的二十年间，基于光栅的X 射线干涉仪获得了大量的关注，在成像方法［1-9］、器件制作［10-13］和实际应用［14-17］等方面取得了一系列的研究成果。双相位光栅干涉仪由于无需分析光栅，能实现大视场、高剂量利用率的X 射线相衬和暗场成像［18-24］。双相位光栅干涉仪的劳条件（Lau condition）影响着成像条纹的对比度，而条纹对比度又影响了系统的信噪比。对于双相位光栅干涉仪的劳条件，有学者利用直观的几何关系［20］，分别求出光源移动对两块相位光栅产生的条纹移动量，再将两个条纹移动量相减获取劳条件。他们认为对于双π 相位光栅干涉仪，在多色光照明下的源光栅周期为单色光照明下的源光栅周期的两倍。其理由则是在多色光照明下，相位光栅的零级衍射不为零。但这无法解释对于π 相位光栅的Talbot-Lau 干涉仪，其源光栅周期无论在单色光照明时还是多色光照明时均是相同的。对于双相位光栅干涉仪灵敏度，大多数研究人员都是直接在DONATH T 等［25］建立的Talbot-Lau 干涉仪灵敏度模型上进行推导［21，26］。但DONATH T 等建立的灵敏度模型本身存在一定程度的不合理，因此在该模型上获取的双相位光栅干涉仪灵敏度也存在着一定的问题。本文将给出新的灵敏度模型，该模型巧妙地利用了系统的劳条件求取双相位光栅干涉仪的灵敏度。

1 理论计算与数值模拟

1.1 双相位光栅干涉仪的劳条件

一般而言，双相位光栅干涉仪的劳条件指的是源光栅的周期。从Talbot-Lau 干涉仪劳条件的获取过程中可知，劳条件可以利用波动光学进行推导。因此，对于双相位光栅干涉仪劳条件的获取，也可以尝试从波动光学的角度出发。在单色光照明时，利用菲涅耳衍射可以得到当点光源从光轴上的位置G0移动到G0'时（如图1），双相位光栅干涉仪在成像平面上的复振幅分布可表示为

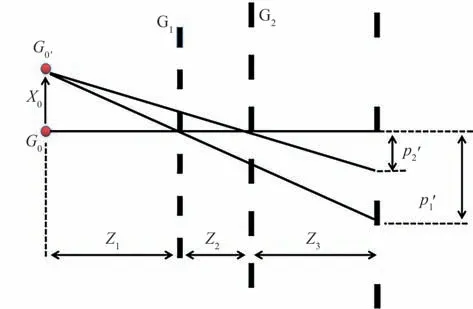
图1 双相位光栅干涉仪中的劳条件示意Fig.1 Illustration of the Lau condition of the dual phase grating interferometer

式中，A5为相位常数，在考虑相对光强时可以忽略。a n、b m、p1、p2分别为相位光栅G1和G2的傅里叶系数和周期。z1、z2和z3分别为G0到G1、G1到G2和G2到成像平面的距离，x3为成像平面上的坐标。p、M1和M2则分别表示为

从式（1）可以看出，当光源移动x0距离后，光栅G1的“像”移动了，光栅G2的“像”移动了。和分析双相位光栅干涉仪成像条纹周期时类似［27］，考虑振幅最大的条纹移动量，即可将问题极大简化。对此，同样分两种情况进行考虑，即双π 相位光栅干涉仪和双π/2 相位光栅干涉仪。

1）双π 相位光栅干涉仪

一般而言，单色光照明时双π 相位光栅干涉仪中相位光栅正负一级衍射形成的干涉条纹振幅最大。该条纹在光源有偏移量x0情形下的表达式为

式（5）化简后可得

为了使点光源G0'形成的条纹（式（6））和光轴上G0点形成的条纹能够相互加强，应使二者的相位差为2π的整数倍，即

式中，p3是条纹周期，将条纹周期［22］代入式（7），化简后可得

式中，x0既可取正值，也可取负值，其物理意义为G0'可以在G0的上下两边分布。式（8）即为两个不同位置的点源所成像的条纹能够互相加强的条件，此时x0即是源光栅的周期p0。因此，双π 相位光栅干涉仪的劳条件为

式（9）的正确性已由文献［22］中的实验所验证。需要强调的是，在多色光照明下，双π 相位光栅干涉仪的源光栅周期既可能由式（9）决定，也可能由式（12）决定。因为从式（7）可知，双相位光栅干涉仪的源光栅周期与成像条纹周期紧密相连。而在多色光照明时，双π 相位光栅干涉仪的成像条纹周期既可能由相位光栅正负一级衍射形成的干涉条纹决定［22］，也可能由相位光栅的零级和正负一级衍射形成的干涉条纹所决定［27］。有学者认为，双π 相位光栅干涉仪在多色光照明时由于相位光栅零级衍射的存在，成像条纹周期一定是单色光照明时的两倍［20］。但实验结果［22］却表明条纹周期在多色光照明时并不一定会加倍。一个类似的例子是，对于π 相位光栅Talbot-Lau 干涉仪，分数泰伯阶处的成像条纹周期在单色光照明和多色光照明时是相同的。其根本原因在于，系统的成像条纹周期不是由周期最大的干涉条纹决定，而是由振幅最大的干涉条纹所决定。在双π 相位光栅干涉仪满足对比度极大值条件时［27］，相位光栅的零级和正负一级衍射形成的干涉条纹振幅远不如相位光栅正负一级衍射形成的干涉条纹振幅大，此时成像条纹周期由相位光栅正负一级衍射形成的干涉条纹所决定。当双π 相位光栅干涉仪不满足对比度极大值条件时，条纹周期则主要由相位光栅的零级和正负一级衍射形成的干涉条纹所决定。

2）双π/2 相位光栅干涉仪

对于双π/2 相位光栅干涉仪，振幅最大的干涉条纹是零级和正负一级衍射形成，即

式中，ϕ代表初相，其具体形式不影响劳条件的结果。化简式（10）后可得

图2 点源在光轴上的G0处与光轴外的G0'处形成的仿真条纹Fig.2 The simulation fringe formed by the point source G0 on the optics axis and the point source G0' off the optics axis

表1 双相位光栅干涉仪的仿真参数Table 1 The simulation parameters of the dual phase grating interferometer

1.2 Talbot-Lau 干涉仪的灵敏度

在DONATH T 建立的Talbot-Lau 干涉仪灵敏度模型［25］中，隐含着两个有争议的假设。第一个假设是沿着光轴传播的X 射线通过物体后不发生折射。该假设只有在X 射线垂直入射到均匀的物体上时才能成立，对于一般的样品是不成立的。第二个假设是光源发出的X 射线与光轴的夹角很小，并且这些傍轴X 射线被物体折射后，能够与光轴相交，且交点恰好落在分析光栅所在的平面。对于X 射线而言，空气的折射率会略大于物体的折射率，所以X 射线通过物体后，一般是离光轴越来越远，而不是越来越近。即使X 射线通过物体后能与光轴相交，其交点未必就落在分析光栅所在的平面上。接下来将给出新的灵敏度模型，并首先将该灵敏度模型应用于简单的Talbot-Lau 干涉仪上，再过渡到复杂的双相位光栅干涉仪的情形。

图3（a）表示当物体处于相位光栅G1与成像条纹之间时的情形，G0表示源光栅中的一透光点。为简便起见，图3 中忽略了分析光栅。G0到G1、G1到成像条纹和物体到成像条纹的距离分别为z1、z2和zD。图中蓝色和紫色曲线分别表示有无物体时的成像条纹，两条条纹实际处于同一平面上（为了便于说明两条条纹之间存在横向位移，将其画在了不同平面上）。

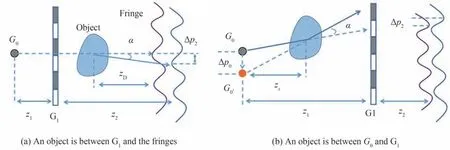
图3 Talbot-Lau 干涉仪示意Fig.3 Illustration of the Talbot-Lau interferometer

当一束X 射线通过物体后，会产生大小为α的折射角。X 射线的折射使得条纹产生了Δp2的移动和Δϕ的相移，据此可得

将式（13）带入式（14）后，再由灵敏度的定义［25］可得

式中，SD为物体处于相位光栅与成像条纹之间时的系统灵敏度，p2为成像条纹的周期。上述推导过程在文献［19，28］中也有论述，其过程符合直观的想象。

图3（b）表示当物体处于G0与G1之间时的情形，其中zS表示物体与G0的距离。当X 射线通过物体后，会引起条纹产生大小为Δp2的移动。如何求解Δp2，是求解灵敏度的关键所在。本文提出一个新的灵敏度模型：物体引起的条纹移动与光源位置变化引起的条纹移动是等效的。据此，可以将X 射线通过物体后的折射线作一反向延长线，该反向延长线与源光栅所在的平面相交于点G0'。如果把G0'想象成是一虚拟光源，那么折射线则是从G0'发出的直线。此时，问题就从物体所产生的条纹移动转化为了光源移动所产生的条纹移动。本文将该方法称为“折射反投影法（Refraction Back Projection，RBP）”。令G0与G0'之间的距离为Δp0，由小角近似可知

由Talbot-Lau 干涉仪的劳条件可得

式中，p0为源光栅的周期，对式（17）两边取微分得

再将式（16）和（18）代入式（14），可得当物体处于G0和G1之间时系统的灵敏度SS，表示为

再利用一次劳条件式（17），式（19）可化简为

在获取式（20）的过程中，关键在于提出的新灵敏度模型，“折射反投影法”则给出了将物体对X 射线的折射作用转换成光源移动的具体方法，而劳条件起到了联系光源移动与条纹移动的桥梁作用，三者之间层层递进。从光路可逆性的角度来理解的话，即想象图3（b）中的X 射线是从右往左传播的，而探测器在G0所在的位置，那么“折射反投影法”则和应用于图3（a）的方法完全对称。DONATH T 建立的灵敏度模型至少依赖于两个假设，而提出的新灵敏度模型则只有一个假设，因此该灵敏度模型更合理，推导过程也更简单。

1.3 双相位光栅干涉仪的灵敏度

通过之前的分析可知，利用RBP 可以非常有效地求取Talbot-Lau 干涉仪的灵敏度。接下来，将利用RBP 推导双相位光栅干涉仪的灵敏度。

图4（a）为物体处于相位光栅与成像条纹之间时的情形。G1、G2分别表示周期为p1、p2的相位光栅。z1、z2和z3分别是G0到G1、G1到G2和G2到成像条纹之间的距离。Δp3为物体所引起的条纹移动量。此时，系统灵敏度的推导过程和式（13）与（14）相似，系统灵敏度SD表示为

式中，p3为成像条纹的周期。而图4（b）为物体处于G0和G1之间时的情形，当物体插入时成像条纹产生了Δp3的移动和Δϕ的相移，据此可得

图4 双相位光栅干涉仪示意Fig.4 Illustration of the dual phase grating interferometer

接下来则需要计算物体所引起的条纹移动量Δp3。利用式（7），将x0换成p0后可得利用条纹周期表示的劳条件

对式（23）两边取微分后可得

利用RBP 可以获得Δp0，即式（16）。将式（16）和（24）代入式（22）可得

再次利用双相位光栅干涉仪的劳条件，将式（23）代入式（25）得

利用灵敏度的定义，可以获得物体处于G0和G1之间时双相位光栅干涉仪的灵敏度

可见，双相位光栅干涉仪与Talbot-Lau 干涉仪的灵敏度具有相同的形式。在上述的推导过程中相位光栅的类型没有预先假定，意味着式（21）和（27）对于双π 相位光栅干涉仪和双π/2 相位光栅干涉仪都是适用的。

而当物体处于两块相位光栅之间时，如图5，其灵敏度的表达式则略微复杂一些。由于一阶分数泰伯像比其它高阶的分数泰伯像具有更高的对比度和亮度，因此将它作为中间光源。首先考虑图5（a），物体处于G1和其一阶分数泰伯像之间时的情形。G1与物体、G1与'和与G2之间的距离分别为z23、z21和z22。由于物体的引入，的移动量为(z21-z23)α。参考式（18）可得

图5 物体处于两块相位光栅之间Fig.5 Illustration of an object between the two phase gratings

将式（28）代入式（22）可得

利用灵敏度的定义，由式（29）可得物体处于G1和之间时的灵敏度

2 结果与讨论

从式（21）和（27）可知，双相位光栅干涉仪的灵敏度一般低于Talbot-Lau 干涉仪的灵敏度。这是因为在两种干涉仪中，物体到光源或成像条纹的距离差别不大。而双相位光栅干涉仪的条纹周期或源光栅周期则比对应的Talbot-Lau 干涉仪条纹周期或源光栅周期大一个数量级以上。因此，对于双相位光栅干涉仪，目前难以实现大视场的同时还能实现高的系统灵敏度。

式（21）和（27）给出的灵敏度与文献［21］中基于DONATH T 灵敏度模型获得的结果几乎完全一致。二者的区别在于，对于双π 相位光栅干涉仪，文献［21］的结果中衍射级次m的值只取了2。而本文的理论结果则表明，该衍射级次m的值既可以取2，也可以取1，其取值决定于成像条纹周期在多色光照明时是否是单色光照明时的两倍［27］。而当双相位光栅干涉仪按照文献［26］提出的方式将系统分为前后两个级联的Talbot-Lau 干涉仪进行处理时，式（21）和（27）给出的灵敏度与文献［26］给出的灵敏度是一致的。当双相位光栅干涉仪的系统参数偏离两个级联的Talbot-Lau 干涉仪所需的参数时，二者计算出来的灵敏度则不一定相同。其原因在于文献［26］给出的灵敏度依赖于级联的Talbot-Lau 干涉仪，而本文结果则不受此限制。

3 结论

本文首先利用波动光学获取了双相位光栅干涉仪的劳条件，并指出双相位光栅干涉仪的源光栅周期与成像条纹周期紧密关联。由于双π 相位光栅干涉仪的条纹周期在多色光照明时不一定是单色光照明时的两倍，因此，双π 相位光栅干涉仪的源光栅周期在多色光照明时也不一定是单色光照明时的两倍。同时，针对Talbot-Lau 干涉仪和双相位光栅干涉仪的灵敏度分析，本文提出了新的灵敏度模型，并据此模型提出了“折射反投影”法。该方法可以充分利用系统的劳条件，将光源的移动和成像条纹的移动巧妙地联系在一起，从而化简了系统灵敏度的推导过程，对于双相位光栅干涉仪灵敏度的设计具有重要的理论价值。