太赫兹时域光谱技术研究S 掺杂GaSe 晶体的电导率特性*

李高芳 殷文 黄敬国 崔昊杨 叶焓静 高艳卿 黄志明† 褚君浩

1) (上海电力大学 电子与信息工程学院,上海 200090)

2) (中国科学院上海技术物理研究所 红外物理国家重点实验室,上海 200083)

本文采用透射式太赫兹时域光谱技术研究0.3—2.5 THz 范围内本征GaSe,S 掺杂质量分数为2.5 %GaSe(GaSe: S(2.5%))和S 掺杂质量分数为7% GaSe(GaSe: S(7%))晶体的电导率特性,并利用Drude-Smith-Lorentz 模型对复电导率进行拟合.研究发现GaSe 晶体的电导率实部随S 掺杂浓度的增大而减小,主要是由于S 掺杂使GaSe 晶体的费米能级逐渐向电荷中性能级转移,载流子浓度下降引起的.本征GaSe 和GaSe:S(2.5%)在约0.56 THz 处有明显的晶格振动峰,而GaSe: S(7%) 在0.56 THz 附近无晶格振动峰,这主要是由于S 掺杂提高了晶体的结构硬度,减弱了晶体的层间刚性振动.且3 个样品均在约1.81 THz 处存在明显的窄晶格振动峰,强度随S 掺杂浓度的增大先减小再增大,主要是由于S 掺杂降低了GaSe 的局部结构缺陷,减弱了窄晶格振动峰强度,而过量的S掺杂生成β 型GaS 晶体,进而增加晶体的局部结构缺陷,窄晶格振动峰强度随之增强.GaSe 晶体约在1.07 THz和2.28 THz 处的宽晶格振动峰强度随S 掺杂浓度的增大而减弱甚至消失,主要是由于S 掺杂产生替位杂质(S 取代Se)和GaS 间隙杂质,降低了基频声子振动强度,从而减弱了晶体二阶声子差模引起的晶格振动.结果表明,S 掺杂可以有效抑制GaSe 晶体的晶格振动,降低电导率,减少在THz 波段的功率损耗.此研究为低损耗THz 器件的设计和制作提供重要的数据支撑和理论依据.

1 引言

III-VI 族层状半导体[1]是一类具有通式MX(M=Ga,In;X=S,Se,Te)的分层金属硫属元素化合物,由于其优异的非线性光学性质,广泛应用于光开关器件[2]、光化学电极[3]和太赫兹辐射[4]等新兴领域中.GaSe 晶体作为典型的III-VI 族层状半导体[5],具有较大的非线性系数(d22=54 pm/V),较宽的透光范围(0.62—20 µm),较低的吸收系数(α＜ 1 cm—1)和较大的双折射率(Δn=0.34)等优异的光学性质[6],使其在THz 辐射源[7-+]、光电探测器[10]、气体传感器[11]和高效太阳能电池[12]等领域具有广阔的应用前景.

然而,由于弱的层间范德瓦耳斯力作用,本征GaSe 晶体硬度较低,且存在大量的结构缺陷[13],加剧了对太赫兹(terahertz,THz)波的吸收[14],限制了其在THz 波产生和传输中的应用.通过掺杂不仅可以增强GaSe 晶体的机械性能,而且能够改善其结构缺陷,提高光学性质[15].Ku 等[14]制备了不同Te 掺杂浓度(质量分数为0.01%—2.07%)的GaSe 晶体,发现Te 掺杂GaSe 晶体的硬度比本征GaSe 晶体提高25%,且Te 掺杂质量分数为0.07%GaSe 晶体利用光整流法辐射的THz 效率比本征GaSe 晶体增强20%.Huang 等[16]研究发现Al 掺杂质量分数为0.13 % GaSe 晶体硬度是本征GaSe 晶体的 2.6 倍,在0.83—14 µm 范围内吸收系数低至0.1 cm—1.Rak 等[17]研究发现In 掺杂质量分数为3% GaSe 晶体的显微硬度比本征GaSe晶体增大至少6.2 kg/mm2,在2—18 µm 范围内吸收系数低至0.1 cm—1,且晶体在5—10 µm 范围内透过率比本征GaSe 晶体提高至少10%.

相比于Al,Te 和In 等低浓度掺杂,高浓度的S 掺杂可大幅改善GaSe 晶体缺陷,提高晶体光学性质.Huang 等[18]制备的S 掺杂质量分数为2.38%GaSe 晶体硬度比本征GaSe 晶体提高34%,且该晶体在0.62—12.5 µm 范围内的红外透过率比本征GaSe 略高.Molloy 等[19]利用太赫兹时域光谱(terahertz time-domain spectroscopy,THz-TDS)技术分析了不同S 掺杂浓度(质量分数分别为1.1%,2.5%,5%,7%,11 %)GaSe 晶体在THz 波段的吸收系数,研究发现S 掺杂质量分数为2.5% GaSe晶体的o 波吸收系数最小,S 掺杂质量分数为11%GaSe 晶体的e 波吸收系数最小.Guo 等[6]研究发现在S 掺杂质量分数为0.05%—11%时,随着S掺杂浓度的增大,GaSe 晶体的短波吸收边明显蓝移,有效消除了近红外激光泵浦的二阶非线性光子吸收.Kokh 等[20]制备了不同S 掺杂浓度的GaSe晶体,发现S 掺杂质量分数为3% GaSe 晶体在0.3—4 THz 范围内的吸收系数比本征GaSe 下降了3 倍.

本课题组前期对不同S 掺杂浓度GaSe 晶体进行了窄带和宽带THz 辐射的研究.首先,利用共线差频法研究了S 掺杂GaSe 晶体的窄带THz辐射,发现S 掺杂质量分数为2.5% GaSe (GaSe:S(2.5%))晶体在1.62 THz 处输出的最大峰值功率为21.8 W,比本征GaSe 晶体在相同频率的输出功率提高了45%[21].其次,利用光整流法研究了本征和S 掺杂GaSe 晶体的宽带THz 辐射,发现GaSe:S(2.5%)晶体的THz 辐射峰值比本征GaSe 晶体提高了28.3%[22].

本文利用THz-TDS 技术研究0.6—2.5 THz范围内本征GaSe,GaSe: S(2.5%)和S 掺杂质量分数为7% GaSe (GaSe: S(7%))晶体的电导率特性,发现其电导率实部随S 掺杂浓度的增大而减小,且本征GaSe 和GaSe: S(2.5%)在约0.56 THz 处有明显的晶格振动峰,而GaSe: S(7%) 在0.56 THz附近无晶格振动峰;同时观察到3 个样品均在约1.81 THz 处存在明显的窄晶格振动峰,强度随S 掺杂浓度的增大先减小再增大,且本征GaSe 晶体在1.07 THz 和2.28 THz 处出现明显的宽晶格振动峰,GaSe: S(2.5%)晶体仅在1.07 THz处出现微弱的宽晶格振动峰,而GaSe: S(7%)晶体未出现宽晶格振动峰,并利用Drude-Smith-Lorentz 模型对复电导率进行拟合.此研究为低损耗THz 器件的设计和制作提供重要的数据支撑和理论依据.

2 实验设备

实验采用透射式THz-TDS 技术测量不同S 掺杂浓度GaSe 晶体在THz 波段的光谱特性.该实验使用的是英国剑桥Teraview 公司生产的型号为TeraPulse 4000 的THz 脉冲光谱仪,设备光源采用中心波长为780 nm 的飞秒光纤激光器,产生和探测THz 波的实验装置均采用低温生长的GaAs 光电导天线.

基于光电导天线产生和探测的透射式THz-TDS 系统光路示意图如图1 所示,主要由飞秒光纤激光器、THz 产生装置、THz 探测装置和时间延迟系统等部分组成,飞秒激光和THz 波均为水平偏振.飞秒光纤激光器产生的脉冲激光被分束器分为抽运光和探测光,抽运光经凸透镜聚焦在GaAs 光电导天线上,产生光生载流子,被外电场加速辐射出THz 脉冲.THz 脉冲被第一个离轴抛物镜准直、第2 个离轴抛物镜聚焦于被测样品上,透过样品后将载有样品信息的THz 波与探测波共同作用在THz 探测装置上.利用探测光路上的光学延迟系统调整抽运光和探测光之间的时间延迟,最终获得不同样品的THz 时域光谱.

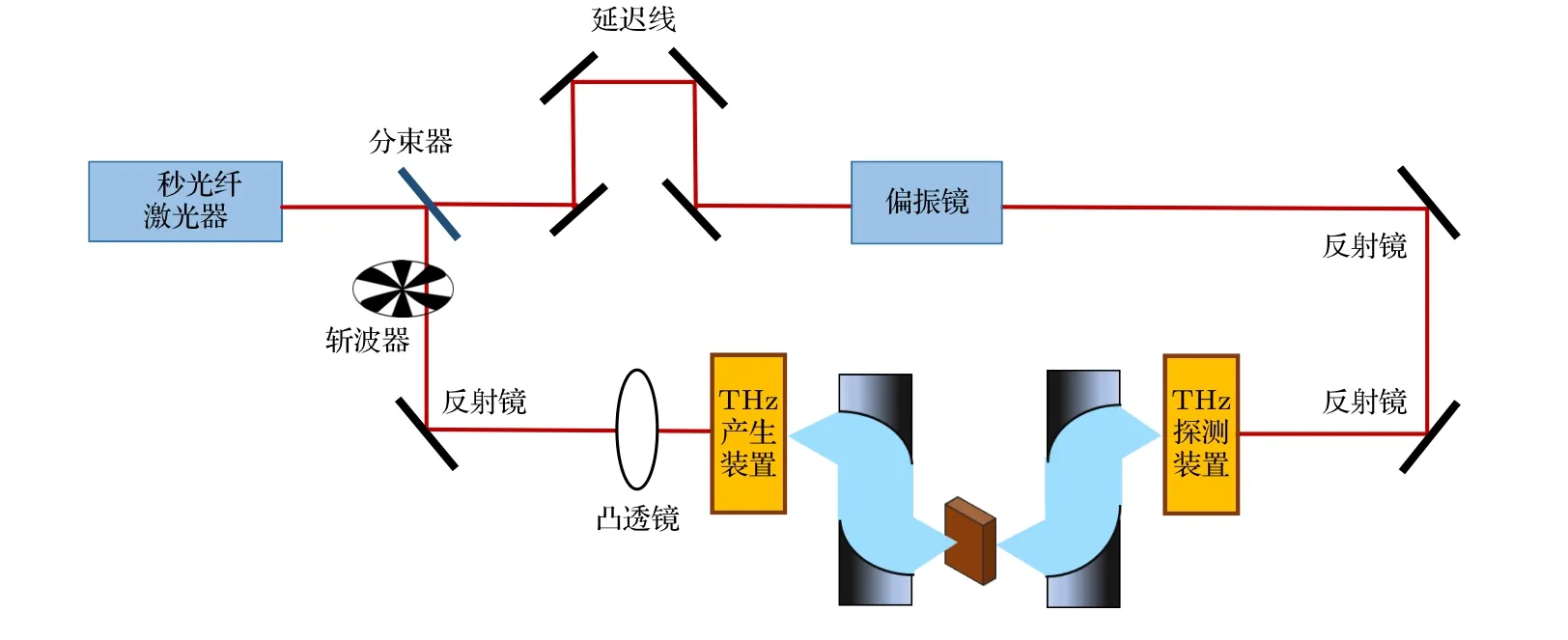
图1 透射式THz-TDS 系统实验装置示意图Fig.1.Schematic diagram of experimental setup of transmission THz-TDS system.

实验所用的样品是利用改进的垂直Bridgman法生长的本征GaSe(GaSe),GaSe: S(2.5%)和GaSe: S(7%)晶体[19,23].首先把按化学计量的Ga和Se 以及不同掺杂需要的S 进行称重,分别放入真空石英安瓿中重熔,获得不同S 掺杂浓度的GaSe多晶.在真空环境下将GaSe 多晶密封在退火处理后的石英安瓿中,借助旋转系统使GaSe 多晶在高温区内均匀融化,然后石英安瓿瓶以一定速率轴向移动,依次通过梯度区、低温区,最终冷却析出单晶的GaSe 晶体.3 个样品均是ε 型、z轴切向,表面无涂层且未进行抛光处理,厚度分别为0.55 mm,0.59 mm和0.58 mm,横向尺寸均为1.5 cm×1.5 cm.整个实验在充满N2、湿度为3.8%的室温环境下进行.

3 数据处理

由电磁场理论[24]知道,透过样品前的THz 电场强度(ω) 和透过样品后的THz 电场强度(ω) 的比值可表示为

其中,A(ω) 为透射光强度和入射光强度在频域上的比值,ϕ(ω) 为 相位差,是透过样品的相位φs(ω)和参考相位φr(ω) 之差.

其中,σ1(ω) 是复电导率的实部,σ2(ω) 是复电导率的虚部.

复电导率和复介电常数之间满足关系式[25]:

其中,ε(∞)=7.443 是GaSe 的高频介电常数[26],ε0=8.854 × 10—12F/m 是自由空间介电常数.

复介电常数可表示为

其中,ε1(ω) 为复介电常数实部,ε2(ω) 为复介电常数虚部.

结合(2)式—(4)式,复电导率的实部和虚部可分别表示为

复介电常数和复折射率满足关系式[25]:

其中,n(ω) 为复折射率实部,κ(ω) 为复折射率虚部.则复介电常数的实部和虚部分别表示为

且吸收系数和复折射率虚部满足关系式[27]:

其中,c是真空中的光速.

结合(9)式和(10)式,得到吸收系数和复介电函数的关系为

因此,复电导率的实部和虚部可分别表示为

由(12)式和(13)式可以看出,样品的复电导率除了与高频介电常数ε(∞)和自由空间介电常数ε0有关外,只与复折射率的实部和虚部有关.

4 实验结果和分析

为了研究不同 S 掺杂浓度对 GaSe 晶体电导率的影响,首先测得3 个样品的THz 时域光谱,并经傅里叶变换后计算出3 个样品的折射率(复折射率实部)和消光系数(复折射率虚部),最后由(12)式和(13)式计算出不同 S 掺杂浓度GaSe 晶体的复电导率.用 Ref 表示 N2环境中的 THz 参考信号.

首先测量3 个样品的THz 时域光谱,并经傅里叶变换得到其频谱图.图2(a)为实验测得的N2环境中的THz 参考信号和3 个样品的THz 时域光谱.从图2(a)可以看出,3 个样品的THz 时域光谱的主脉冲较参考信号有较大的时间延迟(约4 ps 左右),且由于3 个样品的厚度和掺杂浓度不同,与THz 参考信号的延迟时间也不同,由图2(a)的插图可以清晰看出,GaSe 的THz 时域光谱与THz 参考信号的时间延迟最小,GaSe: S(2.5%) 的THz 时域光谱与参考信号的时间延迟最大.图2(b)所示为3 个样品THz 时域光谱经傅里叶变换后的频谱图,从图2(b) 可以看出,透过3 个样品的电场强度比参考信号明显降低.

图2(c) 是3 个样品的透射率频谱图,从图中可以看出3 个样品的透射率均随频率的增大而减小,GaSe 整体透过率最小,GaSe: S(2.5%)整体透过率最大.且GaSe 在0.54 THz 和1.79 THz 处有明显的窄透射谷,在1.07 THz 和2.28 THz 处有明显的宽透射谷;GaSe: S(2.5%)在0.57 THz 和1.81 THz 处有明显的窄透射谷,在1.07 THz 处有微弱的宽透射谷;GaSe: S(7%)在1.86 THz 处有明显的窄透射谷,无宽透射谷.这里需要说明的是,3 个样品的窄透射谷频率略有区别,且3 个窄透射谷的频率差与THz 光谱的分辨率相比拟,因此,3 个样品窄透射谷频率的差异可以忽略不计,分别取平均值和中间值0.56 THz 和1.81 THz 作为样品窄透射谷的频率点.

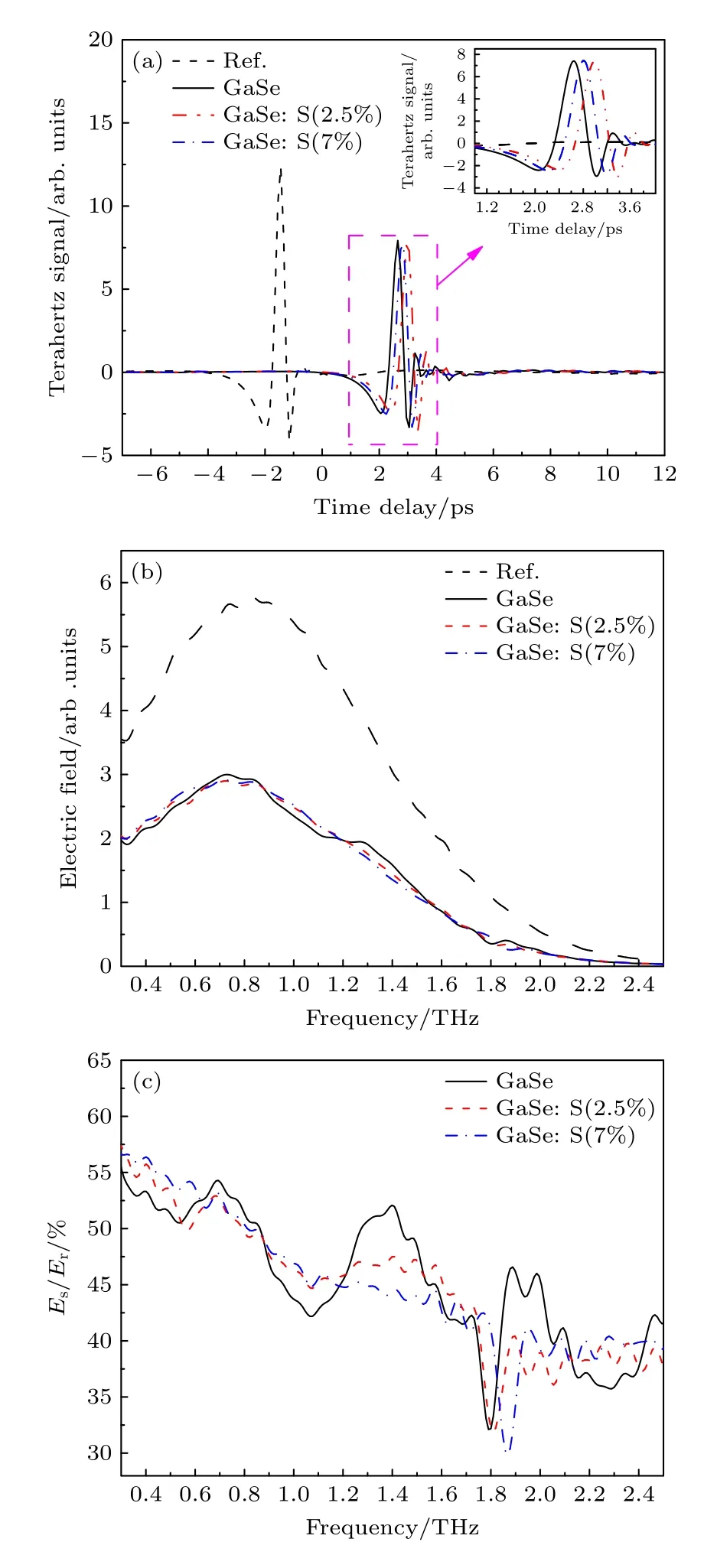
图2 (a)参考信号、GaSe、GaSe: S(2.5%) 和GaSe: S(7%)的THz 时域光谱图,插图是3 个样品THz 时域光谱主峰的放大图;(b) 参考信号、GaSe、GaSe: S(2.5%) 和GaSe:S(7%) 的THz 频谱图;(c) GaSe、GaSe: S(2.5%) 和GaSe:S(7%) 在THz 波段的透射率Fig.2.(a) THz time-domain spectra of the reference signal GaSe,GaSe: S(2.5%),and GaSe: S (7%),the illustration is a magnified view of the main peak of THz time-domain spectrum of three samples;(b) THz spectra of the reference signal GaSe,GaSe: S(2.5%),and GaSe: S(7%);(c) transmissivity of GaSe,GaSe: S(2.5%),and GaSe: S(7%) in THz band.

接下来分别计算出3 个样品的折射率和消光系数,如图3(a)和(b)所示.由图3(a)所示的折射率频谱图可以看出,3 个样品的折射率均随频率的增大而增大,且GaSe: S(2.5%) 的折射率比GaSe略大,而GaSe: S(7%) 的折射率比GaSe 的略小.为了解释折射率随S 掺杂浓度的变化原因,测量了3 个样品的X 射线衍射(XRD)图和(004)晶面的摇摆曲线,如图3(c)和(d)所示.从图3(c)的10°—80°范围内的XRD 图可以看出样品均无其他杂相,结晶为六方ε-GaSe 结构(空间群为Pm2),图中的衍射峰均为(00l)峰.从图3(d)的(004)晶面的摇摆曲线可知GaSe 的半高宽约为0.101°,GaSe: S(2.5%) 的半高宽比GaSe 的小,约为0.090°,这说明对GaSe 进行S 掺杂可以减少结构缺陷,增大晶体结构密度[19],使得GaSe: S(2.5%) 的折射率增大.GaSe: S(7%) 的半高宽比GaSe 和GaSe:S(2.5%)的大,约为0.142°,可能是由于过量的S掺杂使S 原子取代Se 形成GaS 而重整晶体结构,减小了晶格常数,使得GaSe: S(7%) 的折射率减小[28-30].

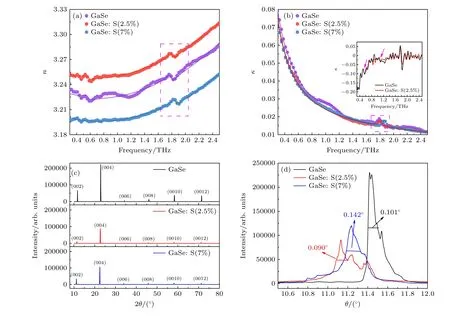
图3 (a) GaSe、GaSe: S(2.5%) 和GaSe: S(7%) 在THz 波段的折射率;(b) GaSe、GaSe: S(2.5%) 和GaSe: S(7%) 在THz 波段的消光系数(实线是折射率和消光系数的拟合结果),插图是GaSe 和GaSe: S(2.5%) 消光系数的一阶导数;(c) GaSe、GaSe: S(2.5%) 和GaSe: S(7%) 的XRD 图;(d) GaSe、GaSe: S(2.5%) 和GaSe: S(7%) (004)晶面的摇摆曲线图Fig.3.(a) Refractive indexes of GaSe,GaSe: S(2.5%),and GaSe: S(7%) in THz band;(b) extinction coefficients of GaSe,GaSe:S(2.5%),and GaSe: S(7%) in THz band (the solid lines are the results of refractive index and extinction coefficient fittings),the illustration is a first-order derivative of GaSe and GaSe: S(2.5%) extinction coefficients;(c) the X-ray diffraction pattern of GaSe,GaSe: S(2.5%),and GaSe: S(7%);(d) the rocking curve of the (004) face of GaSe,GaSe: S(2.5%),and GaSe: S(7%).

消光系数表征晶体在THz 波段光能的衰减,从图3(b)可以看出,在大部分频段GaSe: S(2.5%)和GaSe: S(7%) 的消光系数明显小于GaSe,说明在这些频段内S 掺杂减弱了GaSe 晶体对THz 的吸收.由图3(a)和(b)的紫色虚线框可以看出3 个样品均在约1.81 THz 附近存在拐点,这与窄透射谷的频率一致.另外,从图3(a) 的折射率频谱图可以明显看出,约在0.56 THz 处,GaSe 和GaSe: S(2.5%)存在拐点,而GaSe: S(7%) 不存在拐点.从图3(b)的消光系数频谱图中观察到,GaSe 在1.07 THz和2.28 THz 存在两个弱的宽峰.图3(b) 的插图是GaSe 和GaSe: S(2.5%) 消光系数的一阶求导数,从插图可以看出GaSe 的消光系数在约0.56 THz处存在拐点,而GaSe: S(2.5%)的消光系数除在约0.56 THz 处存在拐点外,在1.07 THz 处还存在一个非常弱的拐点(如插图中的紫色箭头所指处),这与GaSe: S(2.5%)的透射率谱一致.图3(a)和(b)中实线是3 个样品复折射率的拟合结果,具体拟合公式和参数将在电导率分析部分给出.

为进一步分析3 个样品透射率频谱图在0.56 THz,1.07 THz,1.81 THz 和2.28 THz 附 近4 个明显透射谷的情况,由(10)式计算出3 个样品的吸收系数如图4 所示.从图4 可以看出,3 个样品的吸收系数均随频率的增大而增大,且GaSe:S(2.5%) 吸收系数在大部分频率点比GaSe 和GaSe: S(7%) 小,而GaSe: S(7%) 的吸收系数略大于GaSe: S(2.5%),略小于GaSe,这与文献[19]报道的相一致.与图2(c)的透射率频谱图相对应,GaSe 在0.56 THz 和1.79 THz 处有明显的窄吸收峰,在1.07 THz 和2.28 THz 处有明显的宽吸收峰;GaSe: S(2.5%) 在0.56 THz 和1.81 THz 处有明显的窄吸收峰,在1.07 THz 处有微弱的宽吸收峰;GaSe: S(7%) 在1.86 THz 处有明显的窄吸收峰,无宽吸收峰.这里需要说明的是,3 个样品的窄吸收峰频率略有区别,且3 个窄吸收峰的频率差与THz 光谱的分辨率相比拟,因此,3 个样品窄吸收峰频率的变化可以忽略不计,取中间值1.81 THz作为3 个样品窄吸收峰的频率.图4 中实线是3 个样品吸收系数的拟合结果,具体拟合公式和参数将在电导率分析部分给出.

图4 GaSe,GaSe: S(2.5%) 和GaSe: S(7%) 在THz 波段的吸收系数(实线是吸收系数的拟合结果)Fig.4.Absorption coefficients of GaSe,GaSe: S(2.5%),and GaSe: S(7%) in THz band (the solid lines are the results of absorption coefficients fittings).

这些吸收峰主要是由基频声子和二阶声子差模的晶格振动引起的[19,31-+],0.56 THz 处的窄吸收峰是层间刚性振动引起的,1.81 THz 处的窄吸收峰是层内基频声子振动引起的,1.07 THz 处的宽吸收峰是纵向光学声子谐振与层内基频声子的二阶声子差模的晶格振动引起的,2.28 THz 处的宽吸收峰是层内基频声子与层间振动的二阶声子差模的晶格振动引起的[33-+].0.56 THz 处的窄吸收峰强度随S 掺杂浓度的增大而减小,主要是由于掺杂提高了晶体的结构硬度,减弱了晶体的层间刚性振动[31].GaSe: S(2.5%) 在1.81 THz 处的窄吸收峰强度最小主要是由于S 掺杂降低了GaSe 的局部结构缺陷,减弱了层内基频声子的振动强度,减少了对THz 波的吸收.而GaSe: S(7%) 的窄吸收峰强度小于GaSe,但略高于GaSe: S(2.5%),是由于GaSe: S(7%) 中存在一部分过量的S 生成β 型GaS 晶体[29],晶体的局部结构缺陷相比于GaSe: S(2.5%) 增加,对THz 波的吸收也随之略有增强.随着S 掺杂浓度的增大,GaSe 晶体宽吸收峰强度减弱甚至消失,主要是由于S 掺杂产生替位杂质(S 取代Se)和间隙杂质(GaS)[29],降低了基频声子的振动强度,从而减弱了晶体二阶声子差模引起的晶格振动.

然后,根据复折射率和复电导率的关系,计算出不同S 掺杂浓度GaSe 晶体在0.3—2.5 THz 波段复电导率的频谱图,如图5 所示.由图5(a)的电导率实部频谱图可以看出,不同S 掺杂浓度GaSe晶体的电导率实部均随频率的增大而增大,且S 掺杂浓度越高,电导率实部越小,即GaSe 的电导率实部最大,GaSe: S(7%) 的电导率实部最小.同时观察到3 个样品的电导率实部均在约1.81 THz 处存在明显的窄晶格振动峰,且GaSe 在约0.56 THz处出现窄晶格振动峰,在1.07 THz 和2.28 THz 处出现明显的宽晶格振动峰;GaSe: S(2.5%) 在约0.56 THz 处出现窄晶格振动峰,在1.07 THz 处出现微弱的宽晶格振动峰;GaSe: S(7%) 未出现宽晶格振动峰.从图5(b) 的电导率虚部频谱图可以看出,3 个样品的电导率虚部平坦无峰存在,均为负值,且均随频率的增大而减小(绝对值增大).

为进一步分析S 掺杂浓度对GaSe 晶体电导率的影响,需选用合适的模型拟合复电导率.常见的电导率拟合模型有Drude 模型、Drude-Smith模型和Lorentz 模型[36-37],Drude 模型是用来描述振荡电场加速的自由载流子电导率的简单模型[37],该模型假设每个载流子的散射事件都是完全动量随机化的,典型的曲线特征是电导率实部在接近零频率处最大,随着频率的增大而减小,虚部在接近零频率处过原点并随着频率的增大而增大.图5 中不同S 掺杂浓度GaSe 晶体的电导率实部均随频率的增大而增大,虚部为负值且随着频率的增大而减小,故 Drude 模型不能很好地应用于GaSe 晶体复电导率的拟合.Drude-Smith 模型是当晶体边界或一维导电分子边缘发生载流子散射时,完全动量随机散射的假设不再适用,引入一个速度参数持续因子c1来描述微观系统的恢复力或反向散射现象[37].Drude-Smith 模型典型的曲线特征是电导率实部在零频率处最小,随着频率的增加而增大,虚部为负值且随频率的增加而减小,与不同S 掺杂浓度GaSe 晶体复电导率的曲线变化趋势大致相同.Lorentz 模型是用来描述电导率的响应来自由限制环境或强电子-空穴库仑吸引导致完全局域或束缚在激子中的电荷载流子,体现晶格振动效应,其典型的曲线特征是存在明显的晶格振动峰,且不同S 掺杂浓度GaSe 晶体复电导率曲线也存在多处振动峰.

图5 (a) GaSe、GaSe: S(2.5%)和GaSe: S(7%)在THz 波段的电导率实部;(b) GaSe,GaSe: S(2.5%)和GaSe: S(7%)在THz 波段的电导率虚部(实线是Drude-Smith-Lorentz 模型拟合结果)Fig.5.(a) The real part of conductivity of GaSe,GaSe: S(2.5%),and GaSe: S(7%) in THz band;(b) the imaginary part of conductivity of GaSe,GaSe: S(2.5%),and GaSe: S(7%) in THz band (the solid lines are the results of an improved Drude-Smith-Lorentz model fitting).

通过以上对电导率拟合模型的分析,并考虑到晶体中存在电子碰撞效应和晶格振动效应,因此采用Drude-Smith-Lorentz 模型[38,39]对GaSe 晶体电导率进行拟合,其复介电常数的表达式为:

式(14)中的晶格振动频率ωoj由图5(a)中电导率实部的晶格振动峰值频率所决定.GaSe 有4 个晶格振动频率,分别是0.56 THz,1.07 THz,1.81 THz 和2.28 THz;GaSe: S(2.5%) 有3 个晶格振动频率,分别是0.56 THz,1.07 THz 和1.81 THz;GaSe: S(7%) 只在1.81 THz 处有一个晶格振动频率.结合图5 中的复电导率变化规律,将这些晶格振动频率数据分别应用于复电导率的拟合中.

最后,采用Drude-Smith-Lorentz 模型对复折射率、吸收系数和复电导率进行拟合,得到不同S 掺杂浓度GaSe 晶体的等离子体频率ωp、载流子恢复过程的复合时间τ和系统的恢复力或反向散射度c1的值及其平均值,如图6 所示.从图6(a)可以看出,随S 掺杂浓度的增大,等离子体频率向低频移动,载流子恢复过程的复合时间不断增长.从图6(a)的拟合结果的平均值可知GaSe: S(7%)的等离子体频率最小,约为1.32 THz,载流子恢复过程的复合时间最大,约为43.43 fs.GaSe 晶体的等离子体频率随S 掺杂浓度的增大向低频移动,由可知GaSe 晶体的载流子浓度随S 掺杂浓度的增大而下降,这主要是由于随着S 掺杂浓度的增大,GaSe 晶体的费米能级逐渐向电荷中性能级转移引起的[40-42].随着S 掺杂浓度的增大,GaSe 晶体的载流子浓度下降,使载流子碰撞程度减弱,因此,随着S 掺杂浓度的增大,载流子恢复过程的复合时间逐渐增长.从图6(b)可以看出,GaSe 的反向散射度c1最小,且随S 掺杂浓度的增大,c1先增大后减小,主要是因为S 掺杂产生替位杂质(S 取代Se)和间隙杂质(GaS)[29],增加了散射中心,使载流子反向散射度增强,而S 掺杂浓度的继续增大,载流子浓度明显降低,导致载流子反向散射度略有下降.

图6 (a) GaSe,GaSe: S(2.5%)和GaSe: S(7%)的复折射率、吸收系数和复电导率在Drude-Smith-Lorentz 模型下的等离子体频率和载流子恢复过程的复合时间及其平均值;(b) GaSe,GaSe: S(2.5%)和GaSe: S(7%)分别的复折射率、吸收系数和复折射率在Drude-Smith-Lorentz 模型下的系统的恢复力或反向散射度c1 及其平均值Fig.6.(a) The values of the plasma frequency,the complex time of the carrier recovery process and their average for GaSe,GaSe:S(2.5%),and GaSe: S(7%) under the Drude-Smith-Lorentz model of complex conductivity,complex refractivity and absorption coefficient;(b) the values of the recovery force or backscattering degree of the system and the average for GaSe,GaSe: S (2.5%),and GaSe: S(7%) under the Drude-Smith-Lorentz model of complex conductivity,complex refractivity and absorption coefficient.

电导率实部σr与晶体的载流子浓度N和迁移率µ的乘积有关[43],即σr=Nqµ,且晶体的迁移率µ=qτ/m*,可得到,因此,电导率实部与等离子体频率ωp的平方和载流子恢复过程的复合时间τ的乘积有关.将图6 中的拟合参数代入式计算可知,随着S 掺杂浓度的增大,晶体的电导率不断降低,即GaSe 的电导率实部最大,GaSe: S(7%) 的电导率实部最小.这主要是由于S 掺杂产生替位杂质(S 取代Se)和间隙杂质(GaS)[29],使晶体的费米能级逐渐向电荷中性能级转移[39,41],载流子浓度下降引起的.

同时,利用Drude-Smith-Lorentz 模型拟合复折射率、吸收系数和复电导率也得到了不同S 掺杂浓度GaSe 晶体的晶格振动强度Sj和声子驰豫速率Γj及其平均值,如表1—表4 所示.并把表1—表3 的拟合结果取平均值,得到晶格振动强度Sj和声子驰豫速率Γj的值,如表4 所示.一般而言,声子驰豫速率随晶格振动强度的增大而减小,本工作拟合结果同样符合此规律.从表4 可以看出,在1.07 THz 和2.28 THz 处,随着S 掺杂浓度的增大,宽晶格振动峰强度逐渐减弱甚至消失,这主要是由于S 掺杂产生替位杂质(S 取代Se)和GaS 间隙杂质,降低了基频声子振动强度,从而减弱了晶体二阶声子差模引起的晶格振动.在0.56 THz 处,窄晶格振动峰随S 掺杂浓度的增大而减小甚至消失主要是由于S 掺杂提高了晶体的结构硬度,减弱了晶体的层间刚性振动[31].在1.81 THz 处,GaSe的窄晶格振动峰强度最大,其次是GaSe: S(7%),GaSe: S(2.5%) 最小.GaSe: S(2.5%)的窄晶格振动峰强度最小主要是由于S 掺杂降低了GaSe 的局部结构缺陷,减弱了窄晶格振动峰强度.而GaSe: S(7%) 的窄晶格振动峰强度小于GaSe,但略高于GaSe: S(2.5%),这主要是由于GaSe: S(7%)中存在一部分过量的S 生成β 型GaS 晶体[29],晶体的局部结构缺陷相比于GaSe: S(2.5%)增大,窄晶格振动峰强度也随之略有增大.

表1 复折射率的晶格振动强度和声子驰豫速率的拟合结果Table 1.The fitting results of lattice vibration intensity and phonon relaxation rate of the complex refractivity.

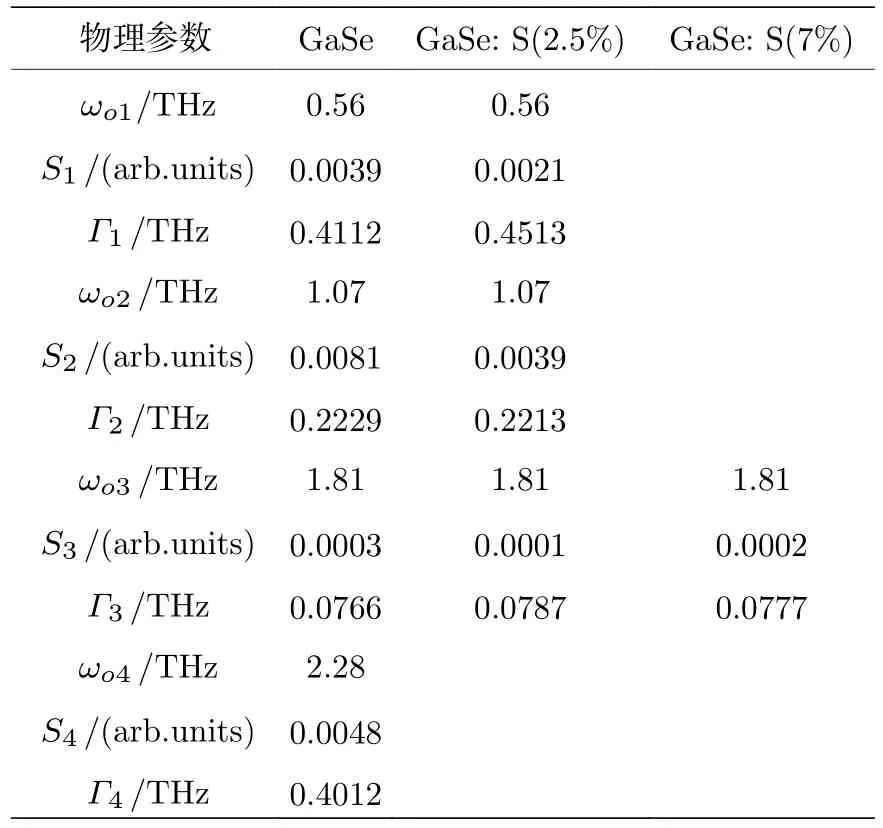
表2 吸收系数的晶格振动强度和声子驰豫速率的拟合结果Table 2.The fitting results of lattice vibration intensity and phonon relaxation rate of the absorption coefficient.

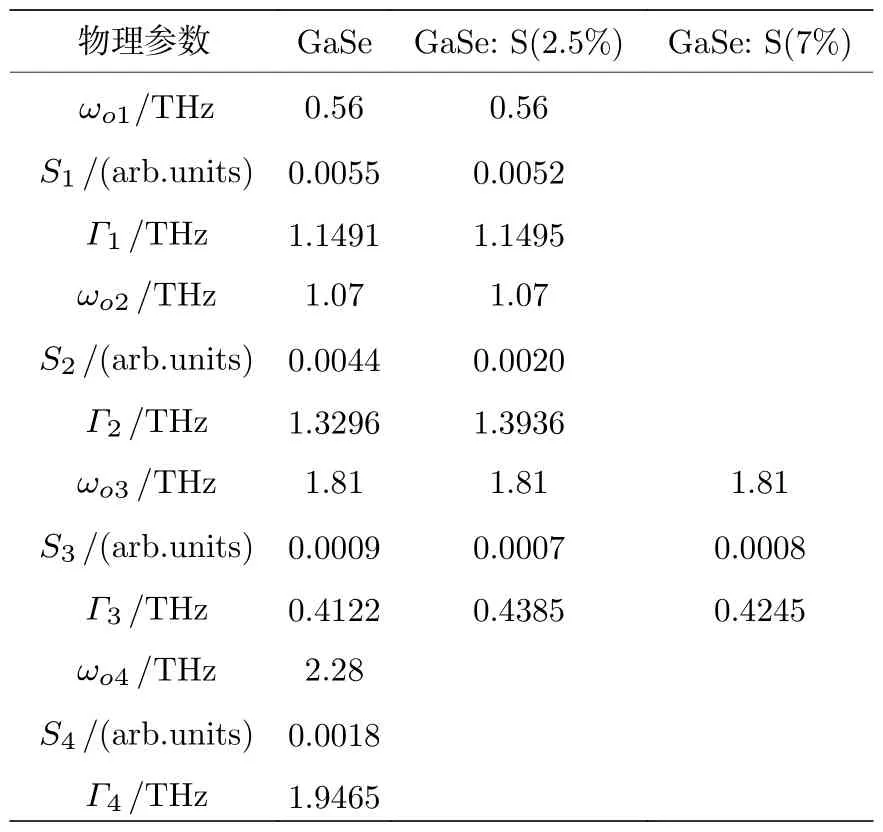
表3 复电导率的晶格振动强度和声子驰豫速率的拟合结果Table 3.The fitting results of lattice vibration intensity and phonon relaxation rate of the complex conductivity.

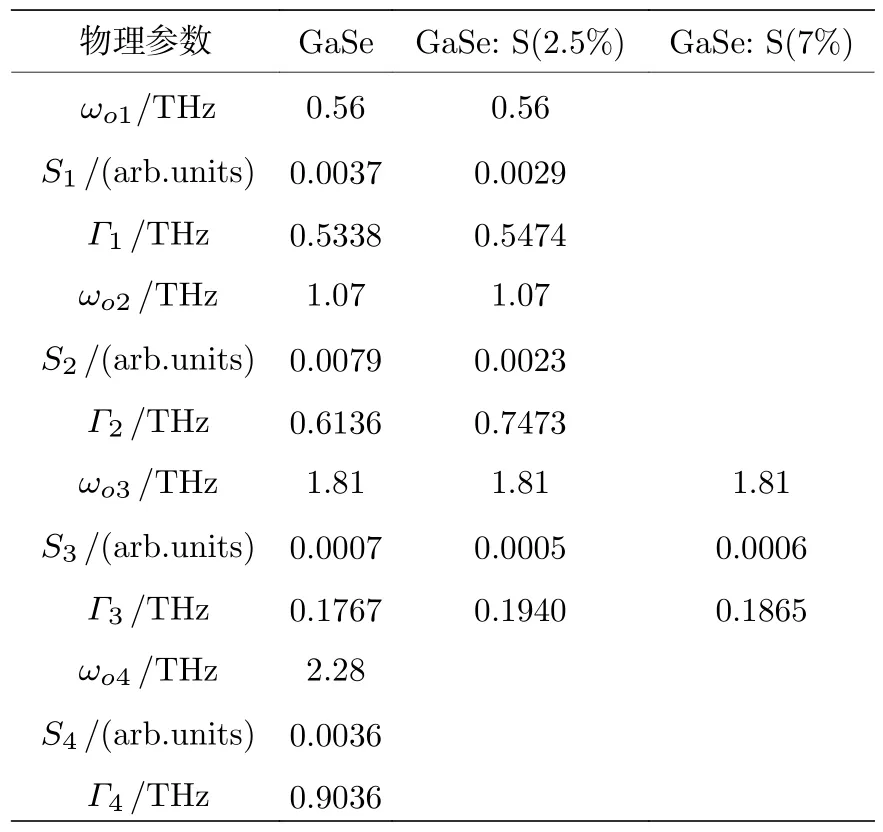
表4 晶格振动强度和声子驰豫速率多次拟合结果各自的平均值Table 4.The averages value of lattice vibration intensity and phonon relaxation rate from multiple fitting results.

5 小 结

综上所述,本文利用THz-TDS 技术,研究了0.6—2.5 THz 范围内GaSe,GaSe: S(2.5%)和 GaSe:S(7%)晶体的电导率特性,并用Drude-Smith-Lorentz 模型对其复电导率进行拟合.研究发现电导率实部均随频率的增大而增大,且随S 掺杂浓度的增大而减小,这主要是由于S 掺杂产生替位杂质(S 取代Se)和间隙杂质(GaS),使晶体的费米能级逐渐向电荷中性能级转移,载流子浓度下降引起的.本征GaSe 和GaSe: S(2.5%)在约0.56 THz 处有明显的晶格振动峰,而GaSe: S(7%) 在0.56 THz 附近无晶格振动峰,这主要是由于S 掺杂提高了GaSe晶体的结构硬度,减弱了晶体的层间刚性振动.同时观察到这3 个样品在约1.81 THz 处均存在明显的窄晶格振动峰,且GaSe 晶体在1.07 THz和2.28 THz 处有明显的宽晶格振动峰,GaSe: S(2.5%)晶体仅在1.07 THz 出现微弱的宽晶格振动峰,而GaSe: S(7%)晶体在0.6—2.5 THz 范围内未出现宽晶格振动峰.随着S 掺杂浓度的增大,GaSe 晶体宽晶格振动峰强度减弱甚至消失,主要是由于S 掺杂产生替位杂质和间隙杂质,降低了基频声子振动强度,从而减弱了晶体二阶声子差模引起的晶格振动.1.81 THz 处窄晶格振动峰强度随S 掺杂浓度的增大先减小再增大,主要是由于S 掺杂降低了GaSe 的局部结构缺陷,减弱了窄晶格振动峰强度,而过量的S 掺杂生成β 型GaS 晶体,进而增加晶体的局部结构缺陷,窄晶格振动峰强度随之增强.结果表明,S 掺杂可以有效抑制GaSe 晶体的晶格振动,降低载流子浓度,减小电导率,减少在THz 波段的功率损耗.此研究为低损耗THz 器件的设计和制作提供重要的数据支撑和理论依据.

感谢俄罗斯托木斯克国立大学西伯利亚物理技术研究所Yury Adreev 教授的讨论.