光伏跟踪支架风荷载的确定及结构优化设计

邓淑丹,林光磊,黄登峰,闫晓磊,黄仕塔,田君福

(1. 福建理工大学 材料科学与工程学院,福建 福州,350118;2. 福建理工大学 机械与汽车工程学院,福建 福州,350118;3. 福建安泰新能源科技有限公司,福建 漳州,363900)

光伏支架作为光伏发电系统的支撑结构,对保证整个系统的稳定高效运行起着重要作用。因此,对光伏支架进行风载计算和结构分析优化以提高其性能是非常有必要的。

在光伏支架的风荷载计算方面,中国[1～2]、美国[3]、日本[4]和欧盟[5]等均制定了相应的规范。学者们还采用风洞实验和计算流体力学(CFD)的方法计算风荷载。文献[6]针对太阳能跟踪器阵列进行了刚性模型测压风洞试验;文献[7]采取计算流体力学理论对水上光伏所受风压进行了研究。为了节约施工材料、降低施工成本,不少研究也对光伏支架进行结构分析,为光伏电站支架的合理设计提供依据。文献[8]运用有限元分析软件对新型光伏系统进行了静、动态性能分析;文献[9]利用有限元分析软件对固定式可调光伏支架结构进行了力学结构分析;文献[10]使用有限元模拟方法重点探究横梁间距、立柱数量、前后立柱间距等结构参数对承载能力的影响;文献[11]采用拓扑优化设计方法实现了光伏支架的轻量化。然而,上述研究没有将数值模拟和各国经验公式进行相互验证,对光伏支架结构优化的研究也还有提升的空间。

本研究利用FLUENT软件进行光伏支架风载分析,在对其施加风荷载后进行结构动、静态性能分析,并在HyperStudy平台中开展光伏支架尺寸优化研究,选出轻量化效果显著的方案进行性能验证。

1 光伏组件表面的风荷载计算

本研究的项目所在地福建省厦门市经常受到台风等灾害性天气的影响,风荷载是光伏跟踪支架的主要荷载,准确计算风荷载尤为重要。目前国内没有专门计算光伏发电阵列风荷载的规范,多数研究将日本的计算规范作为我国在太阳能光伏系统设计的重要参考依据[12]。

1.1 参照日本标准的光伏支架风载计算

在日本设计规范《光伏天线阵结构的负载设计指南》(JIS C 8955:2017)[4]中,风荷载w的计算公式为:

w=CwqAw

(1)

式中,Cw为风力系数,Aw表示受风面积;q表示风压。

正风压时,风力系数Cw按公式(2)计算:

Cw=0.85+0.055θ-0.005θ2

(2)

负风压时,风力系数Cw按公式(3)计算:

Cw=0.85+0.048θ-0.005θ2

(3)

式(2)(3)中,θ为光伏板与地面的倾角(5°～60°);风压q的计算公式为:

q=0.6V2IJ

(4)

式中,V表示风速;I表示用途系数;J为环境系数。本研究的太阳能光伏发电系统的为普通的太阳能光伏系统,I值取1。环境系数J的计算公式为:

(5)

式中,Er代表由式(6)或式(7)计算出的平均风速在高度方向上的分布的系数;Gf代表阵风效应系数,取3.1。

当H小于等于zb时,

(6)

当H大于zb时,

(7)

式中,zb、zG、a由表1可得,地形粗糙度取第Ⅳ类;H表示光伏阵列离地的平均高度。

表1 地形粗糙度分类Tab.1 Classification of terrain roughness

1.2 光伏支架风场数值模拟

计算流体力学(CFD)是利用计算机技术求解流体力学控制方程,可对各种流体问题进行数值模拟分析。随着计算机技术的发展,CFD技术被逐渐应用于大跨桥梁、大型复杂屋盖、建筑火灾、污染物扩散、城市规划等领域。本研究利用计算流体力学仿真软件Ansys Fluent计算光伏跟踪支架所受风压情况,选用长度7 m、宽度4 m、高度2.5 m的光伏跟踪支架模型作为标准模型。流体域选取如下:光伏支架高度h,风场入口面至建筑物迎风面距离为5h,计算域两侧面边界出流面至建筑物侧面距离为5h,计算域顶部至光伏支架顶部距离为7h,出流面至光伏支架背风面距离为13h。0°风向角、30 °高度角下计算域图见图1(a),简化的光伏板模型见图1(b)。

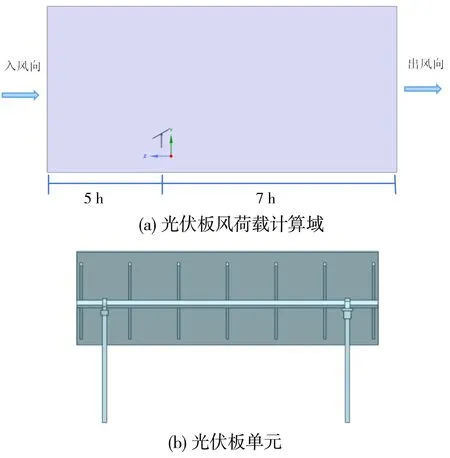
图1 光伏板风场模拟模型Fig.1 Simulation model of photovoltaic panel wind farm

应用Fluent meshing软件进行流程化网格划分,首先在spaceclaim中对几何模型进行清理以及拓扑检查;再导入Fluent meshing中几何模型生成面网格,按照一些尺寸函数及尺寸分布对面网格进行重构;随后基于面网格的重构情况来进行流体区域的抽取生成体网格,生成体网格后即可直接提交到solution模式下进行求解。本次计算采用不可压缩理想气体、高雷诺数、三维稳态、标准k-epsilon湍流模型,并利用标准壁面函数及SIMPLE算法进行数值求解。

1.3 仿真结果与规范对比分析

在风向角为0°、倾角为30°的情况下,设入口边界为速度入口(velocity-inlet),速度分别为10、20、30、40 m/s;设出口边界为压力出口(pressure-outlet),出口壁压为0 Pa。图2为正风压作用下,10、20、30、40 m/s的光伏板迎风面所承受的压力分布图。光伏组件倾角为30 °,不同风速下的压力数值模拟结果与公式计算结果如表2所示。

图2 光伏组件CFD仿真结果Fig.2 CFD simulation results of photovoltaic modules

表2 CFD仿真结果与规范值对比Tab.2 Comparison between CFD simulation results and standard values

由于日本规范没有考虑中心轴承受的力矩作用,因此其计算的风压大于模拟结果。

由表1可知,采用日本规范计算光伏组件所受压力与CFD数值模拟结果比对误差较小,在10%以内。由图2可知,随着风速增大,光伏板迎风面所受压力也增大。如图1(a)所示的风向,光伏组件表面压力最大的位置靠近来流的一端,因为在气流流动的过程中,靠近来流的一端会形成一个高压区域。当气流遇到光伏组件表面时,由于组件的阻挡作用,气流会被分离成两部分:一部分沿着组件表面流动,另一部分则绕过组件继续流动。绕过组件的气流,由于流速增加,会形成低压区域。因此,光伏组件表面就会同时受到来流压力和绕过组件的气流压力的作用,导致靠近来流的一端压力最大。

2 光伏支架结构有限元建模

2.1 光伏跟踪支架三维模型

本研究的对象是铝合金光伏跟踪支架,该模型分为立柱阵列和回转部两个部分,其中回转部主要由主梁、光伏组件构成,立柱阵列主要由立柱、回转座、联动回转构成。立柱与回转座、立柱与联动回转之间通过螺栓固定,回转座与联动回转通过焊接与主梁连接,光伏组件与光伏板边框紧密连接,通过檩条和加强檩条支撑在主梁上。

2.2 有限元模型建立

在建立有限元模型时,除了联动回转、立柱顶座、轴承及轴承座的结构采用实体单元,其余均采用壳单元来划分主体结构,用1D单元模拟焊接、螺栓连接。壳单元基本尺寸为10 mm,实体单元尺寸为15 mm,经过网格划分,一共得到184 495个壳单元、12 852个实体单元、188 862个节点。对于光伏支架来说,施加风荷载的方向为垂直于光伏组件表面,其大小为CFD模拟所得。由此建立的光伏跟踪支架有限元模型及风荷载示意如图3所示。

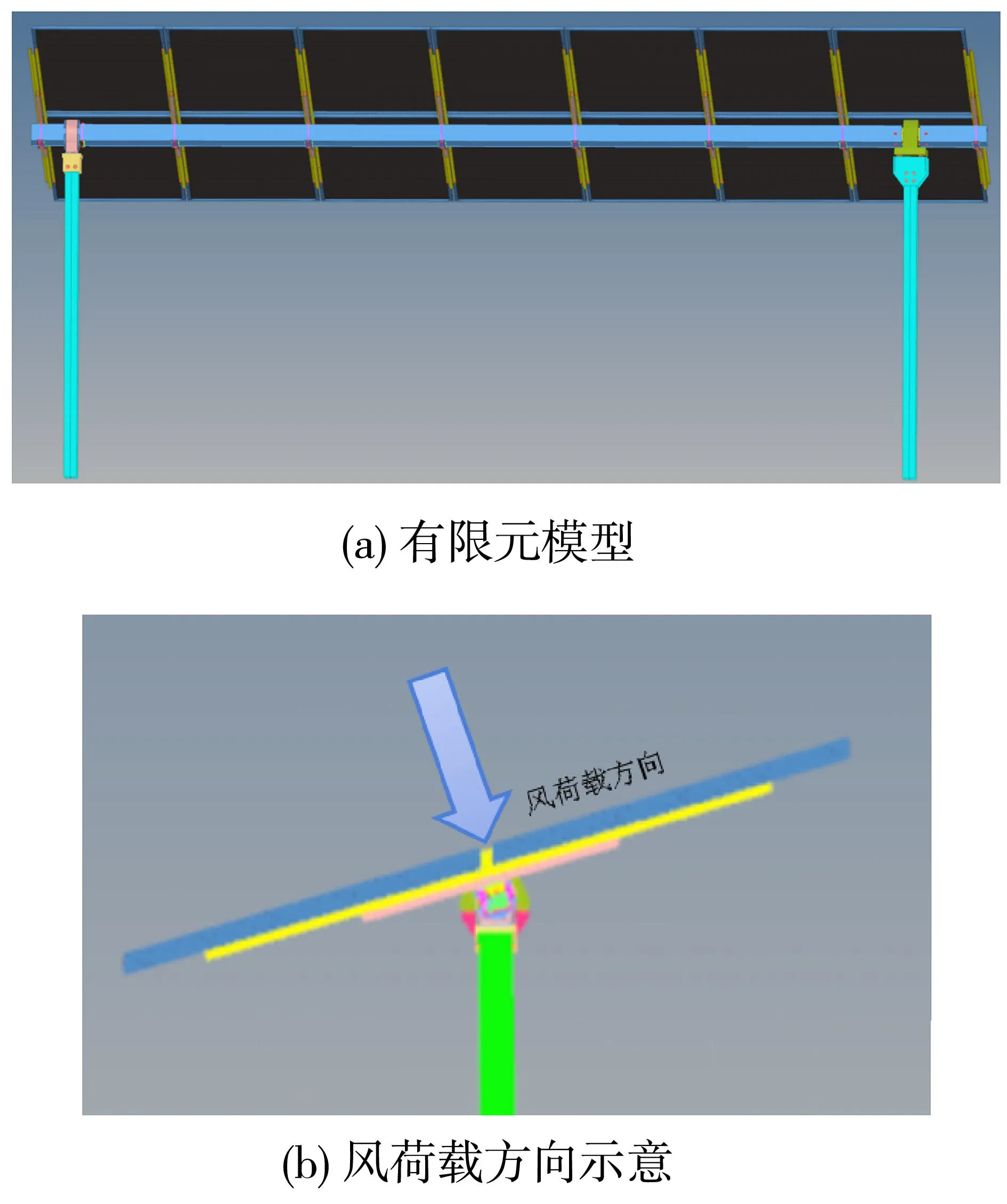
图3 光伏跟踪支架有限元模型Fig.3 Finite element model of photovoltaic tracking support

2.3 材料的选择

光伏跟踪支架模型的支架部分主要运用了铝合金和高强度钢材料,光伏组件运用钢化玻璃材料。光伏支架长年暴露在恶劣的环境中,需要使用防腐材料以免受到氧化、腐蚀。因此光伏系统的立柱部分及旋转部件采用Steel-Q345材料,光伏组件的边框、主梁和檩条部分使用Al-6061/T6铝合金。材料属性参考文献[13],如表3所示。

表3 光伏系统材料性能参数Tab.3 Material performance parameters of photovoltaic system

3 光伏支架动、静态分析

3.1 模态分析

铝合金光伏跟踪支架作为大型的户外使用设备,地震或者脉动风荷载均有可能与跟踪支架产生共振,甚至损坏跟踪支架。因此对跟踪支架进行模态分析是动力学分析计算的重要内容。采用有限元软件的模态分析模块,经过OptiStruct求解器计算,得出前六阶跟踪支架的固有频率及振型。

从表4看出,在光伏组件倾角为0°情况下,光伏跟踪支架结构前六阶固有频率集中在4.28～9.44 Hz,远高于脉动风荷载频率(0.001～0.01 Hz),不会产生共振。从振型上看,光伏跟踪支架结构在第一阶模态无明显振型表现,在第四阶模态表现为弯曲振型,在光伏组件中间位置变形最大,其它阶模态为由于支架的跨距较大引起的扭转振动。

表4 0°倾角下结构前六阶固有频率Tab.4 First six natural frequencies of structure at0° inclination

3.2 刚度分析

光伏跟踪支架在使用过程中受到各种各样的荷载,其中风荷载对光伏跟踪支架寿命影响较大。刚度不足可能会造成光伏跟踪变形过大甚至开裂,特别是立柱、主梁、等关键部位的变形如果过大,其后期维护成本很高,系统甚至可能无法正常运行。根据《光伏发电站设计规范》(GB50797—2012)[2],光伏支架应结合工程实际选用材料、设计结构方案和构造措施,保证支架结构在使用过程中满足强度、稳定性和刚度要求。在正风压情况下,施加垂直于光伏组件表面方向的11 153 N(倾角30°、风速30 m/s时所承受压力)均布荷载,并施加9.8 m/s2的重力加速度,约束支架底座的自由度,进行强度和刚度的校核来判断结构的安全性和稳定性。其位移云图如图4(a)、4(b)所示。

图4 正风压工况下位移、应力云图Fig.4 Displacement and stress cloud diagram under positive wind pressure conditions

根据项目技术指标和国家标准(JIS C 8955 2017),太阳能光伏系统承载支架铝合金主梁的挠度容许值为L/260=28.9 mm,光伏系统的柱顶位移应小于等于柱高的1/70即35.71 mm。根据HyperView中观测的结果,柱顶最大位移为7.03 mm,满足要求;铝合金主梁最大位移为41.31 mm,大于28.9 mm,不满足要求,需进行优化。

3.3 强度分析

在倾角30°、风速40 m/s工况下进行强度分析,光伏跟踪支架在受到自身重量以及风载荷的基础上,结构应力情况如图4(c)、4(d)所示。通过有限元分析发现,光伏支架最大应力在立柱与立柱顶座螺栓连接处附近,为237.53 MPa。因为牵引结构采用Steel-Q345材料,其屈服强度为345 MPa,所以该工况下光伏跟踪支架整体强度符合要求。

4 基于HyperStudy的优化设计

对于光伏跟踪支架的有限元结构分析而言,由于结构的约束条件、优化目标(总质量)和设计变量(各部件壁厚)间并没有显式的数学表达式,无法直接对目标进行优化。因此,本研究选用响应曲面法优化方法,建立以质量最小化为目标优化函数,最大应力和应变为约束条件的响应曲面计算模型,对光伏跟踪支架进行优化设计[14]。

4.1 设计变量的选取

将光伏支架有限元模型导出为fem格式,在Hyperstudy中采用Parameterized File模块对导出的fem文件进行参数化处理。首先确定设计变量为光伏支架部件的厚度,利用Templex语言设置设计变量的上下限,完成设计变量的取值区间定义并生成tpl文件。

表5 拟合精度表Tab.5 Table of fitting accuracy

约束条件包括:

(8)

式中,xl≤xi≤xh,xi是壁厚,xl是壁厚设计范围下限,xh是壁厚设计范围上限;mi为光伏支架质量函数;Fa为光伏支架最大应力;Xa为光伏支架铝合金主梁的挠度值;L是主梁长度;Xb是光伏系统的柱顶位移;h是立柱高度。此次优化设计以件壁厚为设计变量、主梁位移小于等于28.9 mm,立柱位移小于35.71 mm为约束条件、光伏支架质量最小为目标函数。

4.2 试验设计(DOE)

考虑到计算周期问题,采用空间填充的试验设计算法产生样本点,以便于后续响应面的拟合。试验设计中用于空间填充的采样算法包含中心复合设计、Box-Behnken设计、拉丁超立方采样、哈默斯雷采样、可扩展的格栅序列法等。哈默斯雷采样是一种以面代体的取样方法,能在超立方体中随机均匀抽样,且可以用较少的样本点对输出的结果进行评估。本研究采用哈默斯雷采样算法,用作构建响应面近似模型的数据源。DOE分析结果可通过pareto图及Linear Effects图来判断表示各个效应因子对评价指标的重要性程度。哈默斯雷采样结果如图5所示。

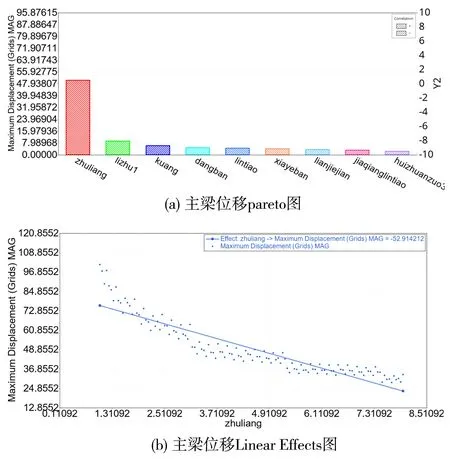
图5 哈默斯雷采样结果图Fig.5 Hammersley sampling results

从图5(a)主梁位移pareto柱状图中可看出,主梁的高度最大表示其厚度对主梁最大位移影响最重要。其中反斜杠填充柱状图表示效应因子和响应为负相关关系,正如图5(b)Linear Effects图所示,斜率为负,代表主梁的厚度越大,其最大偏移量为越小。

4.3 构建近似模型

直接用有限元模型进行仿真优化计算效率低下且对工作站算力要求较高,而且还存在无法获得最优解的可能[15]。近似模型的构建方法是通过对有限次仿真分析结果进行统计和建模,从而找到输入和输出之间的关系。通过数学手段,可以将仿真模型的计算耗时与输入变量之间的关系进行建模,得到一个近似模型。利用这个近似模型,可以在优化过程中代替完整的仿真分析,从而大大降低计算成本。为了兼顾计算效率和拟合精度,本研究采用最小二乘法进行近似模型响应面的拟合。最小二乘法是在拟合的过程中不要求目标函数一定经过数据点,而是使数据点均匀分布在拟合函数两边使误差的平方和最小从而尽可能减小拟合误差,达到较好的拟合精度[16]。

评价近似模型拟合精度的指标有确定系数(R-Square)和相对平均误差(Average)。确定系数(R-Square)用于评价响应面的拟合精度,其值越接近于1,拟合的精度越高。其数学表达式为:

R2=1-SSE/SST

(9)

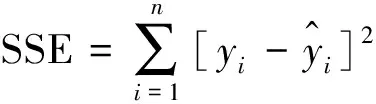
Average是相对平均误差,其值越接近于0,拟合的误差越小。采用R-Square、Average评估响应面拟合的精度,结果如表5所示。根据表5可知,各响应面的R-Square值均在0.9以上,Average值均小于0.3,所以该算法建立的近似模型具有较高的精度。

4.4 自适应响应面优化方法

自适应响应面法可通过舍弃目标响应较大的设计空间,使其在全局最优解附近收敛,并达到更精确的优化结果。所以在面对单目标优化时,自适应响应面法非常高效[17]。目标函数优化收敛迭代曲线如图6所示。

图6 质量迭代曲线Fig.6 Quality iteration curve

基于自适应响应面法采用Hyperstudy进行尺寸优化后,还需要对优化后的结果进行圆整化处理,使其能够符合实际的制造工艺要求。对各变量厚度进行圆整后所得到的结果如表6所示。经过优化,光伏支架质量由810 kg降低至740 kg,减轻了70 kg,减重幅度达19.4%。

表6 变量厚度圆整结果Tab.6 Variable thickness rounding results

将优化后的结构模型与原模型数据对比,得到的结果如表7所示。优化后模型主梁位移最大的位置与优化前一致,均在主梁中间位置,优化后的主梁最大位移为28.63 mm,小于L/260即28.90 mm,满足设计要求。

5 结论

1)本研究运用CFD数值模拟方法计算光伏组件表面所受风荷载压力值。与采用日本规范计算所得光伏组件表面压力值相比,该方法误差较小,在10%以内。因此,流体动力学的仿真计算结果与日本技术规范的计算值是基本一致的。

2)对光伏支架初始结构的有限元分析表明:光伏支架最大应力为237.53 MPa,小于材料的屈服极限345 MPa,满足技术规范要求;柱顶最大位移为10.95 mm,小于35.71 mm,也满足技术指标要求;铝合金主梁最大位移为41.32 mm,大于L/260即28.9 mm,未达到项目技术指标要求,需进行优化。

3)以质量最小化为目标函数,最大应力和应变为约束条件,采用自适应响应面法对光伏跟踪支架进行优化后,其性能满足(JIS C8955-2017)刚强度要求,优化后的重量为740 kg,实现了减重70 kg的目标,从而减少了设计余量并节约了材料成本。