管道封堵气囊结构设计与密封性能研究*

韩传军 费一栗 张芹芹 蔡文博 李言希

(西南石油大学机电工程学院 四川成都 610500)

随着石油和天然气产量的逐渐增加，管道运输已经与铁路、水路、公路、航空并列成为世界五大运输方式。管道运输具有运输量大、无污染、占地少、成本低、不受环环境影响等特点[1-2]。但随着服役年限增加和管道自身材料的缺陷，大多数管道经常会出现腐蚀和破损，同时由于我国地理环境的复杂以及不可预测的地质灾害的频繁发生，也经常导致管道出现意外的损坏。

由于大多数管道布局在野外，一旦管道出现损坏或者破裂，将导致油气停运，给生产生活造成重大影响。而布局在人口密集的市区内的油气管道，一旦受损出现油气泄漏，将导致重大的安全事故发生，造成不可估量的经济损失和人员伤亡。针对这些情况，对于管道损坏的应急性封堵处理装置的研发就显得十分必要[2-5]。

管道封堵机器人作为一种可靠方便快捷的应急修复设备，目前已被广泛地使用在管道修复作业中。在封堵作业时，目前大多采用气囊对破损的部位进行快速封堵，封堵装置按原理一般分为悬挂式、盘式、筒式和囊式封堵等[6-10]。

针对石油和天然气管道破损泄漏情况，本文作者设计一款内封堵导流机器人，其封堵装置采用带压气囊与导流管结合的方式，实现了对管道损坏部位封堵导流的功能。带压气囊的材料为超弹性橡胶材料，其利用橡胶气囊对管壁的挤压产生接触力来实现密封。因此研究气囊的结构以提高其密封性能，对于管道内封堵装置的安全和稳定性具有重要意义。

近年来国内外对管道封堵装置的研究较多，如挪威PSI公司和美国TDW公司研发了先进的管道内封堵装置，可对大型管道的破损进行封堵修复[11]。但在管道封堵气囊密封性方面的研究还不多。王天英等[12]研制了自黏式快速封堵气囊，可以对破损管道进行快速抢险处理，但对气囊的密封的设计主要依靠经验性数据。AMINO等[13]使用X射线成像的方法分析了橡胶与配合表面之间的接触状态。周仕明等[14]基于非线性有限元理论,对充气式自密封气囊结构的密封性能进行了分析。

本文作者基于气囊的实际使用工况，结合理论计算和仿真实验对封堵气囊的接触密封性能进行了研究，优化了气囊结构从而获得了良好的密封封堵性能。

1 管道内封堵导流机器人总体设计

1.1 机器人总体结构

为了满足实际工况和使用要求，管道机器人的总体结构由三大装置构成，分别为动力装置、支撑装置、封堵导流装置。三大装置由万向联轴器连接，具有适应管道变化的过弯自适应能力。总体结构如图1所示。

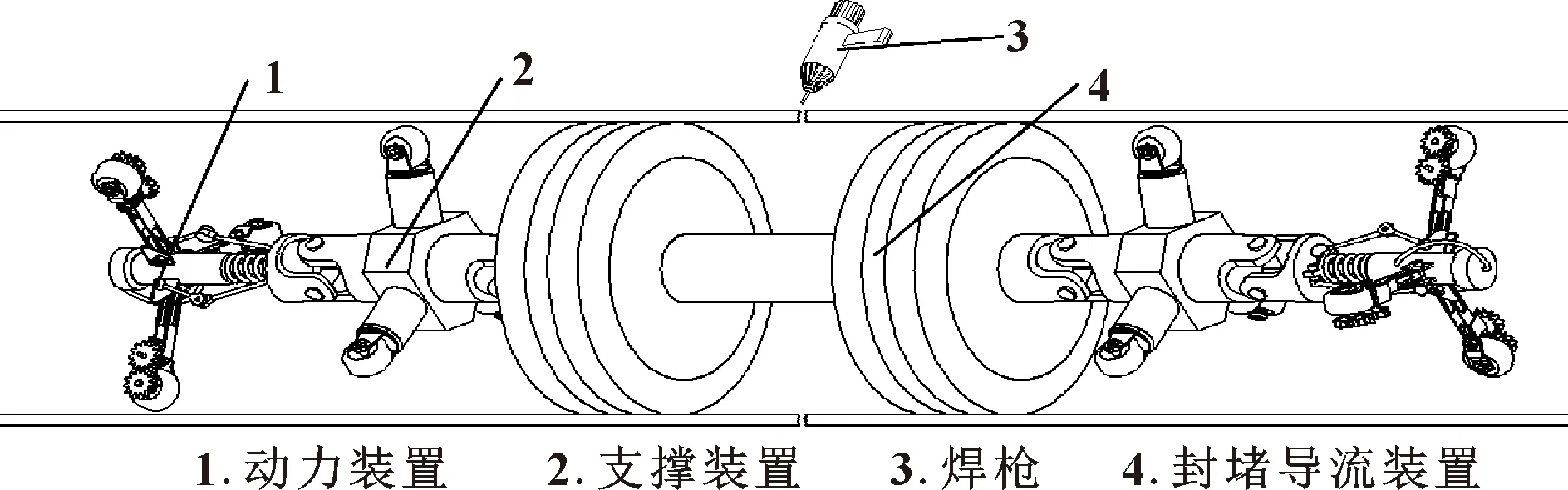
图1 管道封堵导流机器人总体结构Fig.1 Overall structure of pipeline plugging and diversion robot

驱动轮输出动力由电机通过锥齿轮传递给齿轮组，带动轮子转动。机器人前后各安装一个动力装置，可为机器人提供充足的动力。动力装置支撑轮架的伸缩由安装在活塞杆上的压缩弹簧提供所需的动力。因为活塞杆上的弹簧有压缩性，当管径变化时，支撑轮架的连杆可以自由伸展和收缩，这时弹簧起到了很好的自我调节能力，满足支撑轮架的连杆自由张开和收缩所需要的力，整个结构可以很好地适应管道的形变，实现径向大小的自由调节。

1.2 封堵装置设计

如图2所示，封堵装置由气囊、导通管组成，封堵气囊安装在导通管上面，导通管在安装气囊的部位有凸起的卡环，可以实现气囊的定位。当机器人运动到管道的裂缝或断裂的位置时，气囊充气膨胀，与管道的内壁和导通管的外壁形成挤压从而构成一个密封区域，保证液体不从管道裂缝中泄漏，而是从中间导通管流走，实现封堵导流功能。同时，封堵后可以在管道外面对破裂处实施修复作业。

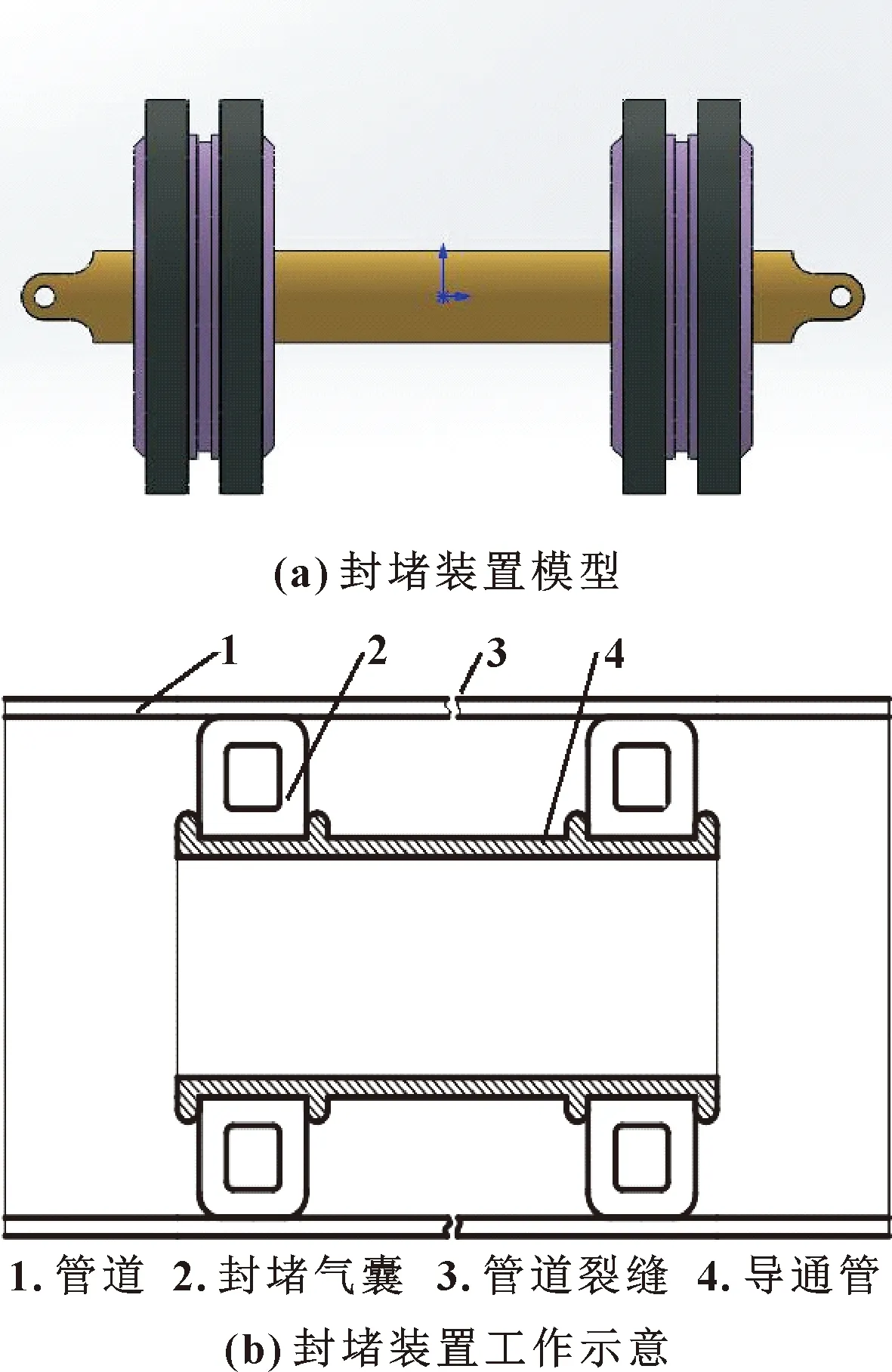
图2 封堵装置Fig.2 Blocking device:(a)blocking device model; (b)schematic of blocking device working

2 封堵气囊性能研究

2.1 封堵气囊模型结构

设计封堵气囊时，将气囊外部整体结构均设计为圆筒状，而气囊内部设计了2种中空结构：一种为等壁厚的圆角方形中空结构，壁厚为20 mm；另一种为圆形中空结构，直径为60 mm。将气囊外部与管道内壁相接触的部位分别设计为直角和圆角2种类型，从而获得了4种不同结构的封堵气囊模型，如图3所示。设计的气囊半径为140 mm,宽度为100 mm，胶筒与管道内壁的距离在未接触时自然状态下空隙为3 mm。通过给气囊充气，使其在不同压力下发生变形与管道挤压和接触，产生足够的摩擦力来抵消液体对端面的压力，从而实现封堵装置的封堵导流功能。

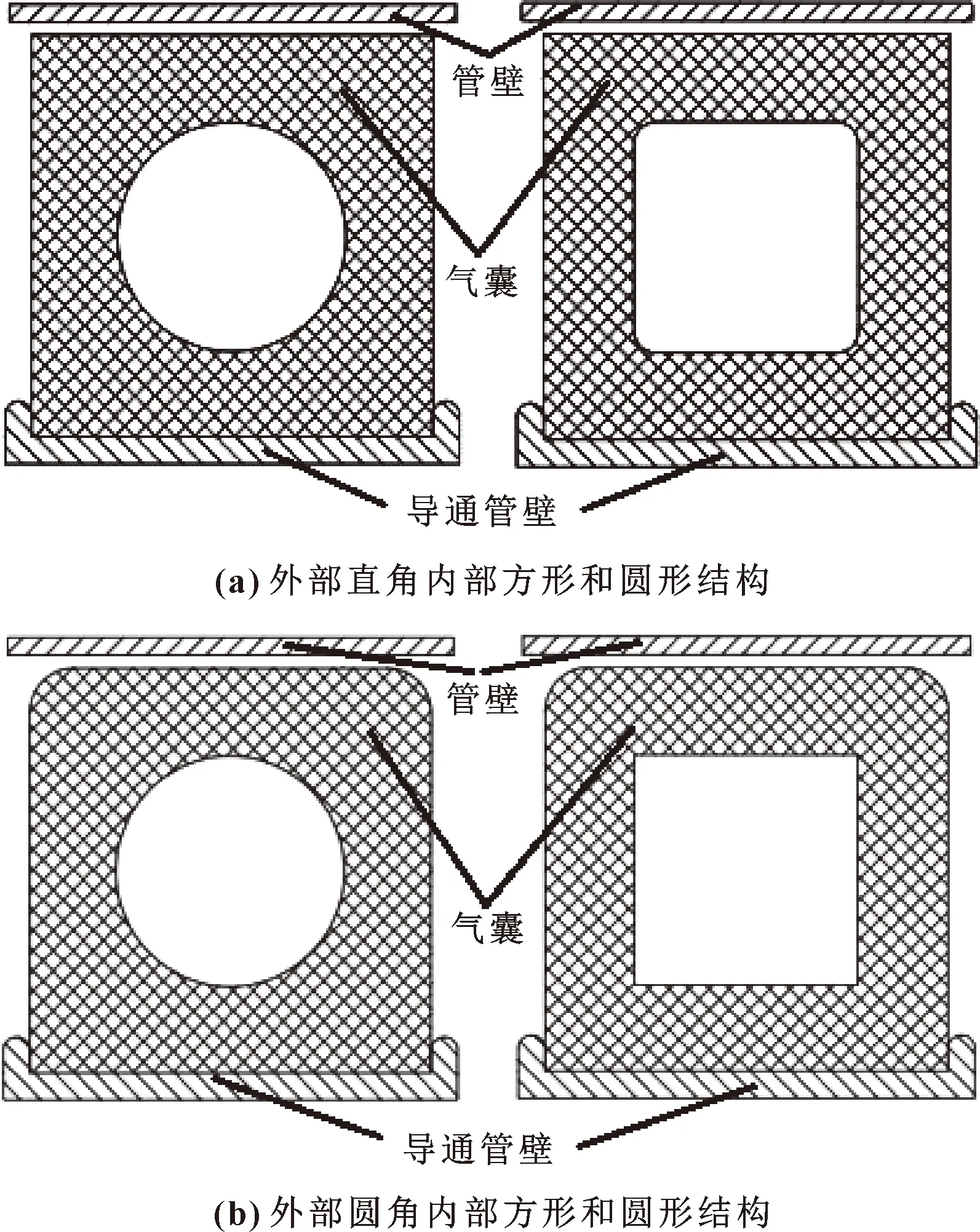
图3 不同结构封堵气囊模型Fig.3 Models of blocking airbags with different structures:(a) structure with outer right angle and inside square and round; (b)structure with outer round and inside square and round

2.2 理论模型的建立

气囊采用丁腈橡胶材料，橡胶材料属于超弹性类型，而丁腈橡胶相比其他类型橡胶材料具有更好的各向同性、高弹性、高变形、压缩性小等特点，因此被广泛应用在各种封隔器和密封气囊上[15-16]。

橡胶材料的有限元分析属于材料非线性，而且气囊在挤压接触部位还有几何非线性和接触非线性，因此利用在求解非线性领域较为成熟的软件ABAQUS进行计算和求解。ABAQUS应用应变势能U表达超弹性材料的应力-应变关系，来取代弹性模量和泊松比。应变势能模型有Mooney-Rivilin模型、Yeoh模型、Valanis 3种。而Mooney-Rivilin模型适用于中小形变的情况，符合文中设计的橡胶气囊的变形情况和实际使用要求，因此文中选用Mooney-Rivilin模型[17-19]。其计算公式为

W=C10(I1-3)+C01(I2-3)

(1)

(2)

式中：C10、C01为材料参数；I1、I2为右柯西-格林变形张量的不变量；σi(i=1,2,3)为X、Y、Z方向的主应变。

式(1)可以较好地表征橡胶材料的力学性能，而且符合橡胶材料在工程中的性能要求。橡胶材料的弹性模量E与材料参数C10、C01的关系式为

(3)

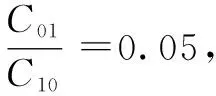
lgE=0.019 8Hr-0.543 2

(4)

文中气囊材料选择硬度为90IRHD的丁腈橡胶材料，根据式(3)、(4)可以求得橡胶材料常数C10=1.926 MPa，C01=0.963 MPa。

2.3 仿真模型建立和计算

由于气囊的几何结构和受力符合轴对称模型，因此在ABAQUS中建立封堵装置的二维轴对称模型。其中气囊与管道内壁和气囊与导通管挡环的侧面建立表面与表面的有限滑移模型；摩擦类型为罚函数的各向同性，切向摩擦因数为0.2，法向摩擦因数为默认的硬接触。管道为45钢，在实际的受挤压过程中几乎没有形变，所以设置导通管和管道为刚体结构；气囊的内圈与导通管接触的部位根据实际工作情况设置为绑定组。

导通管、气囊、管道的网格划分采用CAX4单元，气囊部分采用分区方式进行局部网格加密，并且将气囊部分指定为网格自适应重划处理，以满足非线性变形的求解收敛困难问题。网格划分和边界条件如图4所示。求解分析步设置为几何非线性，自动稳定选择指定耗能分数，参数设置为0.000 2，同时打开使用为应变能设置了最大稳定比例的自适应稳定性选项，参数设置为0.05，进行计算求解。

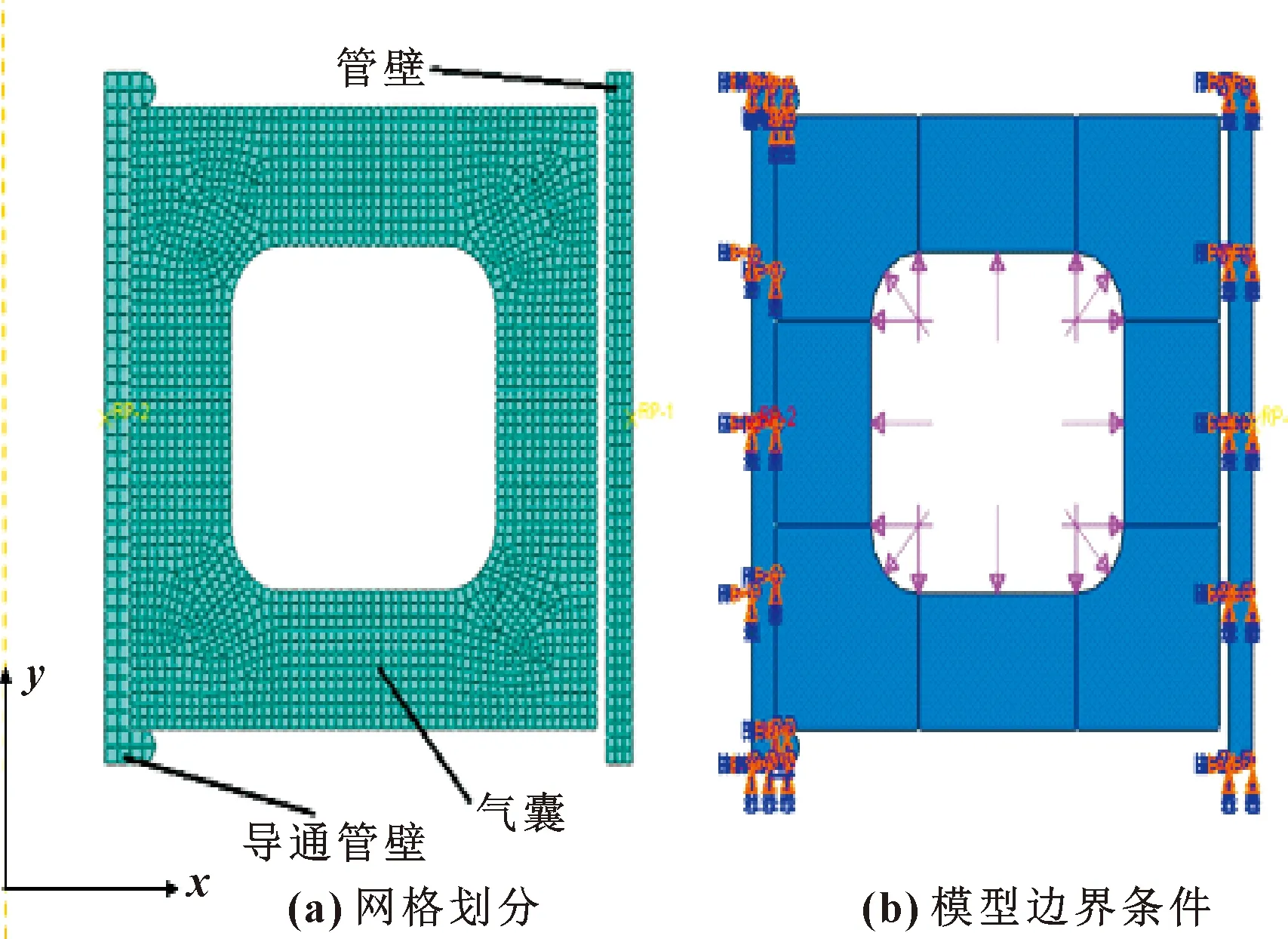
图4 模型网格划分和模型边界条件Fig.4 Model meshing(a)and model boundary conditions(b)

3 计算结果及分析

3.1 网格验证

选取气囊结构为外圆内圆的模型进行网格无关系验证，给内部施加1 MPa均布的压力，分别划分不同数量和质量的网格，网格数量为3 546、4 058、4 529、5 147、5 598、6 078、7 156、7 642。计算得到的最大Mises应力如图5所示。当网格数量到达6 078后应力不再变化，因此选取6 078作为文中模型的网格划分数量。

图5 网格无关性验证Fig.5 Grid independence verification

3.2 不同气囊结构von Mises应力分析

分别在4种模型气囊内部表面施加1、1.5、2、2.5、3 MPa的均布压力，计算4种气囊结构在不同压力下的变形情况。图6所示为1 MPa下4种气囊结构的von Mises应力云图。

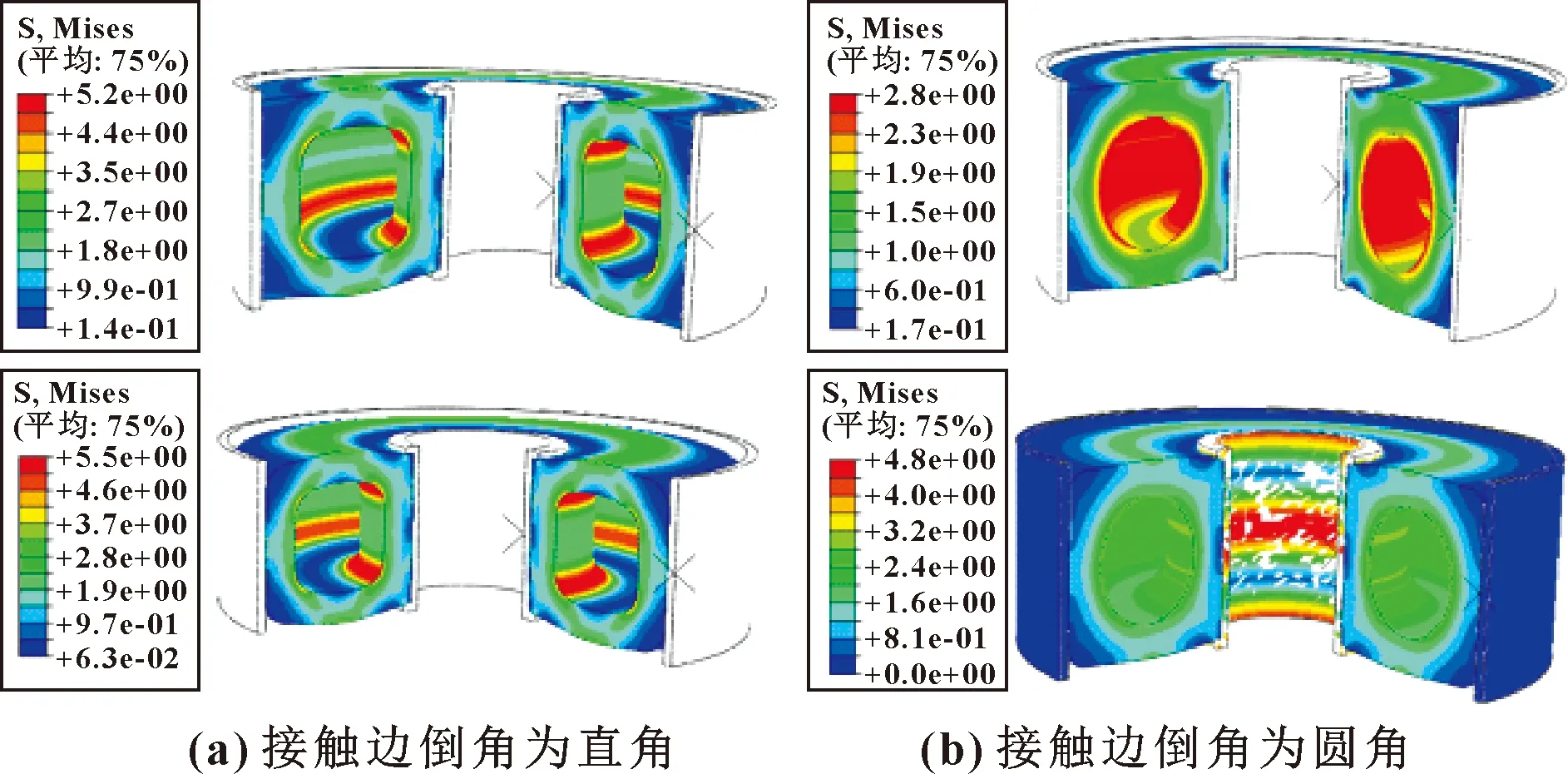
图6 不同气囊结构在1 MPa下应力云图(MPa)Fig.6 Stress cloud diagram of different airbag structures at 1 MPa(MPa):(a)the chamfer of contact edge is right angle; (b)the chamfer of contact edge is rounded

由图6可以看出，4种不同结构的最大应力并不相同，当气囊结构外部接触边倒角都为直角，气囊内部中空结构为圆角方形时应力为5.2 MPa，比内部为圆形中空结构时的应力(2.8 MPa)增加了85.7%，且应力最大部位为气囊内壁圆角中心处。这是由于气囊在压力下发生了较大变形，结构变化突变处会有较大的应力产生而导致。而气囊外部接触边倒角都为直角，内部为2种不同中空结构的气囊模型的最大应力差距并不大，最大应力之差仅为0.4 MPa。应力过大将会导致气囊破坏，因此要分析不同压力下的应力分布，从而选择最优的气囊结构模型。

图7示出了4种气囊结构在不同压力下的最大应力。可以看到，气囊结构外部接触边倒角为圆角，内部为圆形中空结构时，其在不同压力下的应力值最大，且应力的最大值随压力的增加致呈线性增加。而气囊结构外部接触边倒角为直角，内部为圆形中空结构时，随压力的增加其应力增加得较为平缓，且应力的最大值最小，因此该模型具有较好的承压能力。4种气囊结构在最大压力3 MPa下的最大应力为29.72 MPa，相比最小应力(9.971 MPa)增加了2.98倍。因此可以看出，不同形状的气囊结构模型承受压力的能力具有很大的不同。

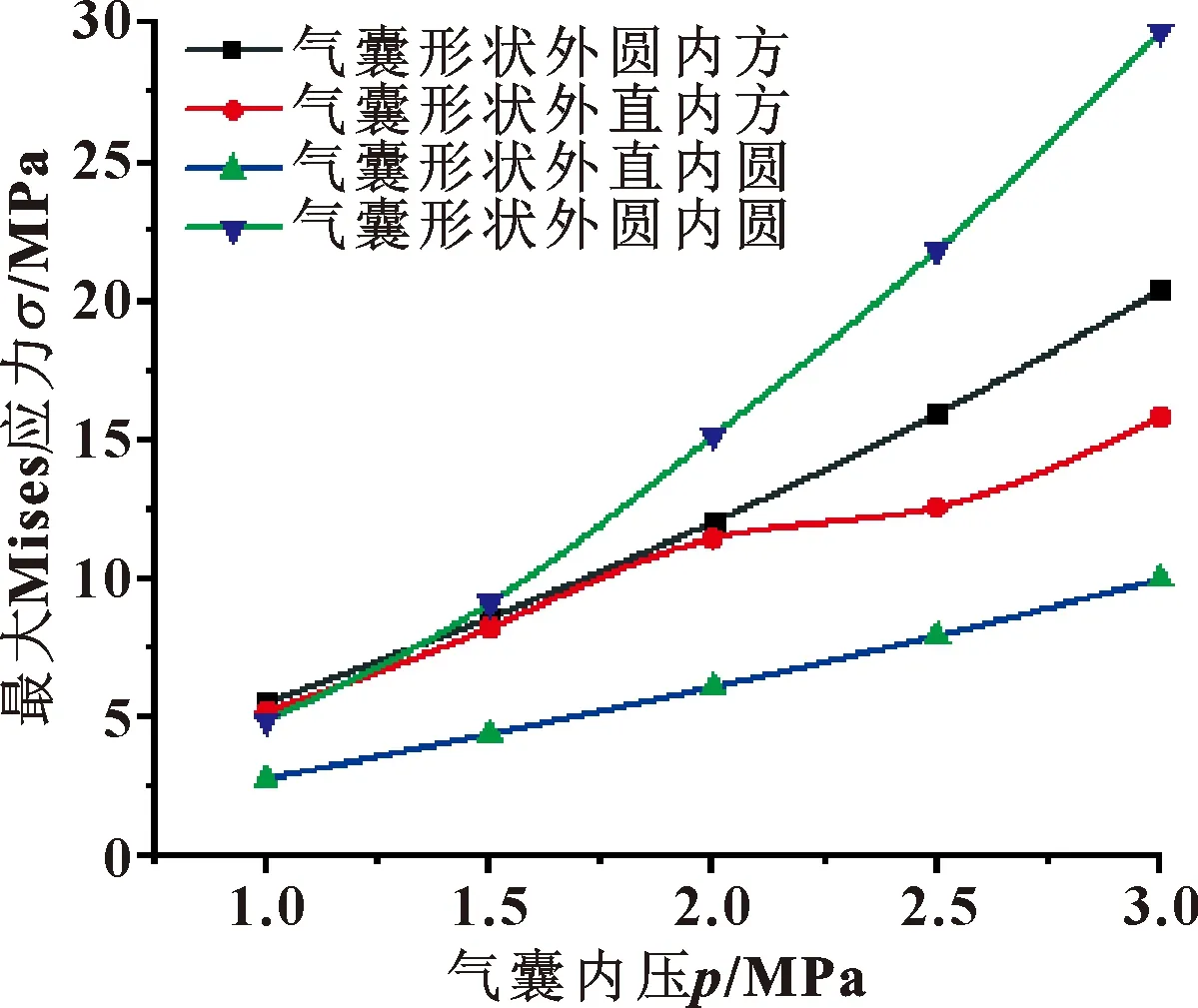
图7 不同压力下4种气囊结构的最大应力Fig.7 Maximum stress offour kinds of airbag structures under different pressures

3.3 不同气囊结构接触应力分析

气囊外表面与管道内壁的接触应力决定了封堵气囊的封堵性能，接触应力越大，封堵能力越强；同时气囊与管壁的接触面积也决定了封堵性能的好坏。

通过软件计算得到4种结构模型在不同压力下的接触应力参数，图8所示是气囊外部接触边倒角为圆角，内部为圆角方形和圆形中空结构的气囊模型，在不同压力作用下的接触应力分布情况。可以看到，随着压力的增加，气囊与管壁的有效接触面积增加，同时接触应力增大，而且接触应力的分布具有很好的对称性。当气囊内部为圆形中空结构时，气囊的最大接触应力大于内部结构为圆角方形中空结构气囊的最大接触应力，且接触面积较大，接触应力为0的部位更少，接触应力在从中间位置往两边的分布也较为平缓。

图8 外部圆角内部方形和圆形结构 封堵气囊模型接触应力分布Fig.8 The contact stress distribution of the airbag models with structures of outer round and inside square and round: (a)model with structure of outer round and inside square; (b)model with structure of outer round and inside round

图9示出了气囊外部接触边倒角为直角，内部为圆角方形和圆形中空结构的气囊模型，在不同压力作用下的接触应力分布情况。可以看到，气囊的接触应力分布规律呈现出对称性，在两边位置具有最大的接触应力，但是接触面积较小；中间位置为第二大的接触应力所在区域，从中间到两边接触应力逐渐减小，接触面积也呈现出相同的规律。同时可以看出，当气囊与管壁接触边的倒角为直角，内部为圆形中空结构时，其具有更好的接触密封性能，最大的接触应力为6.5 MPa，比内部为圆角方形中空结构气囊的最大接触应力(4.8 MPa)增加了35.41%；且较图8中2种结构的最大接触应力(4.2 MPa)提高了近54.76%。因此选择外直内圆结构气囊作为封堵气囊结构具有较好的封堵效果。

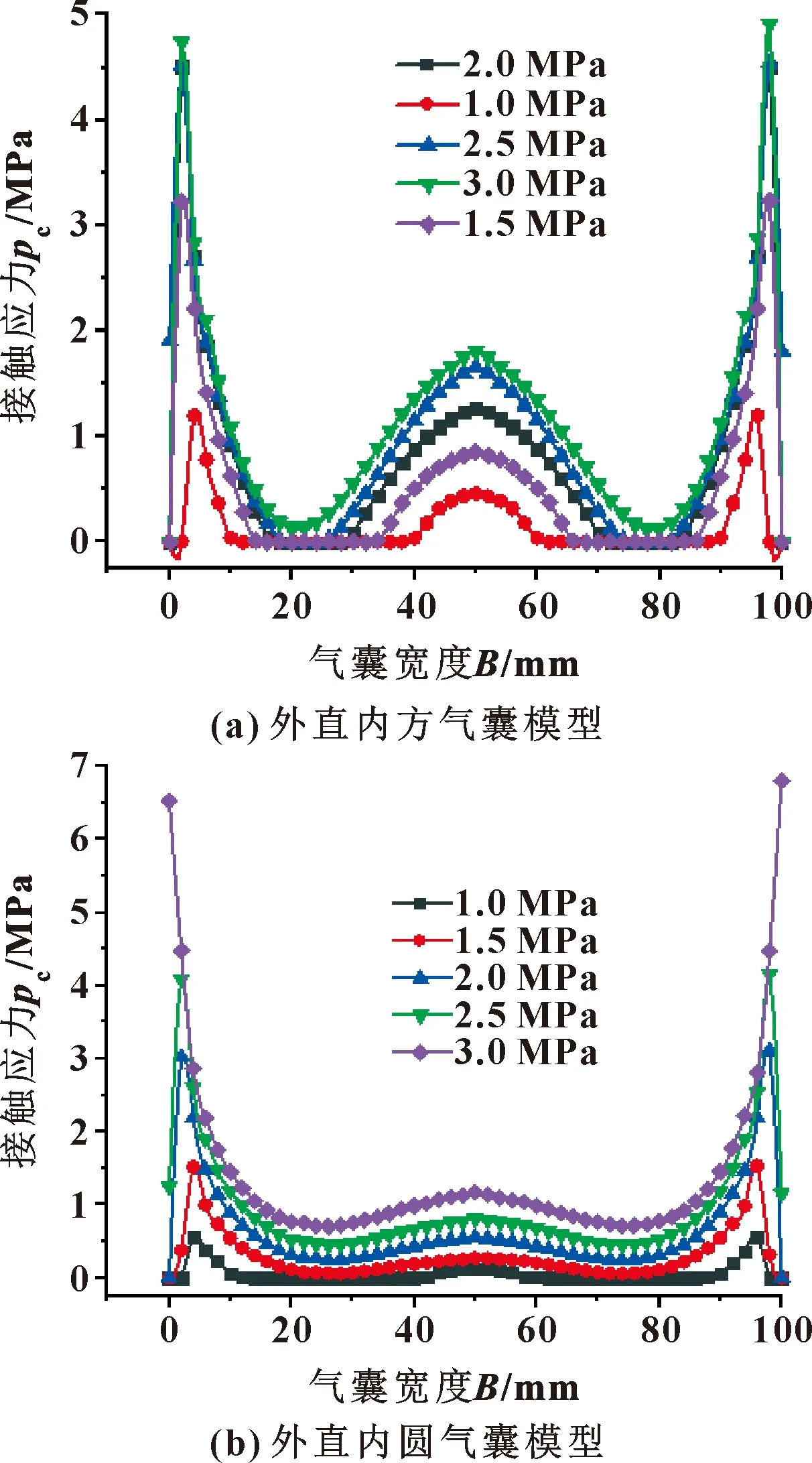
图9 外部直角内部方形和圆形结构 封堵气囊模型接触应力分布Fig.9 The contact stress distribution of the airbag models with structures of outer right angle and inside square and round:(a)model with structure of outer right angle and inside square;(b)model with structure of outer right angle and inside round

4 结论

(1)设计一款具有管道自适应能力的可伸展的管道机器人动力装置，可以随着管道管径和形状的改变而自适应伸缩，具有较好的运动特性。

(2)设计一款充气膨胀性的封堵装置，通过给气囊充气，可实现对管道破损部位的封堵，且封堵装置具有导流功能，能实现在管道不停运的情况下对管道泄漏部位的封堵。

(3)设计并比较4种不同结构的气囊模型的性能，发现当气囊的外部接触边倒角为直角，气囊的内部为圆形中空结构时具有最小的应力分布，有更好的承压性能；同时具有较好的密封性能，能实现管道泄漏部位的封堵。