基于三铰斜拱的不同宽度区段煤柱下底板应力变化规律研究

雒铜童，杨艳国，谯永刚，2，赵金典，马熠坤，王 江

（1.太原理工大学 安全与应急管理工程学院，山西 晋中 030600；2.中国矿业大学 安全工程学院，江苏 徐州 221000；3.山西襄矿集团 上良煤业有限公司，山西 长治 046000）

上保护层开采后，其上覆岩层将发生移动破断和应力重新分布，形成一定的采场空间结构。采场空间结构中破断岩块间的结构发育与力学特征的研究，对于保护层底板应力及被保护层卸压效果的分析尤为重要[1-4]。近距离煤层群上保护层开采时，会留设一定宽度的护巷煤柱，不仅会使底板应力集中，还会在采空区底板产生附加应力，致使卸压效果不充分，从而制约矿井安全生产。因此，针对保护层开采覆岩结构和应力传递规律，专家学者们开展了大量研究。

在覆岩结构力学建模方面：谷拴成等[5]建立了采空区上覆岩体自重荷载向煤柱传递的传力拱模型，给出了煤柱最小留设宽度与煤帮加固范围计算式；文志杰等[6]建立的采场空间模型解释了“裂断拱”和“应力拱”的结构演化规律；于斌等[7]建立了大空间采场覆岩结构力学模型，揭示了其矿压作用机制；李志华等[8]建立了采场覆岩“宏观－大－小”结构力学模型，分析了关键层上覆载荷对关键层破断形式和破断块体稳定性的影响；冯军发等[9]基于煤层开挖力学效应和覆岩运动规律，提出了煤矿采场压力拱的3 种形式；汪锋等[10]通过建立松散层拱承载结构力学模型，揭示了松散层拱的形态、矢跨比和厚度方程；左建平等[11]建立了岩层移动的“类双曲线”模型，能更好地预测地表沉陷范围；岳喜占等[12]构建了上覆煤层“椭圆应力拱”力学模型，计算出了下伏煤层底板的附加应力；石占山等[13]基于垮落范围与压实应力演化的关系，建立了底板卸压值分布状态的弹性力学计算模型。

在覆岩移动与应力传递方面：涂敏等[14]应用数理推导的方式研究大空间孤岛采场覆岩结构演化与区段煤柱的变形和承载特性，确定了影响区段煤柱合理宽度的系统内部参量；程详等[15]在分析覆岩移动破坏特征的基础上，提出了卸压瓦斯综合治理方案；焦振华等[16]用模拟试验、现场实测等手段研究了下保护层开采覆岩运移、裂隙动态演化特征及被保护层变形规律；徐刚等[17]运用FLAC3D软件对上保护层开采后被保护层应力和位移变化规律进行了数值模拟研究；殷伟等[18]研究了混合综采工作面覆岩运移规律和空间结构特征；何团等[19]结合工作面侧向煤体应力形成过程的时间序列，理论分析了工作面侧向煤体应力演化过程；赵雁海等[20]分析了周期断裂覆岩关键块回转接触特征及应力传递规律。

综上所述，目前对于上保护层开采后，区段煤柱影响下的覆岩结构及其对保护层底板附加应力的研究较为鲜见。因此，结合山西上良煤矿实际工程地质条件，在上保护层3-2#煤层充分采动后，构建了采空区三铰斜拱力学模型，理论推导其合理拱轴方程，数值模拟不同宽度区段煤柱的三铰斜拱形态参数和保护层底板应力传递规律，并通过现场试验验证解析解，为区段煤柱的留设宽度及被保护层的安全开采提供了理论依据。

1 三铰斜拱力学模型

1.1 采场三铰斜拱结构

山西上良煤矿井田地质构造简单，构造总体为一单斜，伴有波状小褶曲。走向为NNE—SSW 向，倾向为NW 向。上良煤业3-2#煤层、3-3#煤层具有煤与瓦斯突出危险性，上良煤业为煤与瓦斯突出危险矿井，计划将3-2#煤层作为上保护层进行开采。3-2#煤层厚度0.99～2.92 m，平均1.62 m，属稳定全区可采煤层。3-3#煤层上距3-2#煤层底3.55～14.03 m，平均为9.46 m，下距K7 砂岩12.61 m。煤层厚度1.84～3.02 m，平均2.59 m，结构简单，偶含1 层夹矸，属稳定全区可采煤层。

采场"三铰斜拱"结构示意图如图1。随着上保护层工作面的推进，采空区垮落带上部的规则移动带岩层将断裂成整齐的岩块，受水平推力作用相互咬合在一起，直到受已垮落的岩石支撑达到平衡为止，形成“三铰斜拱”式的铰接关系。三铰斜拱的前拱脚位于区段煤柱上，后拱脚位于采空区内的应力恢复区和重新压实区，其拱轴线以破断岩块的应力传递曲线在空间展布，呈近似“二次曲线”。在采动应力的重新分布下，三铰斜拱结构在开采走向上的竖直平面内不断向采场围岩深部扩展，最终形成了“裂断拱”和“应力拱”的采场覆岩空间结构。

图1 采场“三铰斜拱”结构示意图Fig.1 Schematic diagram of“three-hinged inclined arch”structure in stope

1.2 拱轴方程

上保护层开采后，采空区围岩应力重新分布，底板应力为原岩应力与附加应力之和，原岩应力根据煤层埋深近似计算，因此关键在于对底板附加应力的求解。底板附加应力计算模型如图2。

图2 采场空间一侧底板应力计算力学模型Fig.2 Mechanics model for calculating stress of floor on the one side of stope space

均布载荷下的三铰斜拱力学模型如图3。设煤层开采厚度为hc，煤层埋深为H，区段煤柱塑性区长度为s，工作面倾向为x 轴，z 轴为煤层竖直方向，三铰斜拱倾角为α。取水平简支梁作为三铰斜拱的相应等代梁，定义斜拱的斜推力为T′，斜拱的斜矢高为f′，斜拱跨度为l（l=s+r）。

图3 三铰斜拱及其等代梁力学模型Fig.3 Mechanical model of three-hinged inclined arch and its equivalent beam

按照等代梁计算法[21]，斜拱的支座反力可通过力矩平衡方程求得：

式中：h 为拱顶到起拱线的距离，m；Va，Vb分别为斜拱的垂向支座反力，N；Va0，Vb0分别为等代梁的支座反力，N；T′为斜拱起拱线方向的推力，N。而等代梁相应C 截面的弯矩Mc0可表示为：

式中：lc为拱顶的水平距离，m；q 为三铰斜拱上覆载荷，Pa。

将T′沿水平方向和垂直方向分解，可求得支座的水平反力和垂向反力：

式中：Ta、Tb为水平方向推力，N；l 为斜拱跨度，m。

任取斜拱X 截面，取BX 段作为隔离体，由力矩平衡条件可知，非对称应力斜拱满足平衡条件，斜拱结构任意截面X 处的力矩Mx为：

则斜拱的合理拱轴线方程为：

式（10）中f′和lc仍为未知量，根据拱的稳定性，拱脚处的水平约束力应小于等于拱脚处的最大摩擦力，即：

式中：φ 为内摩擦角，（°）。

在临界状态下，可得拱高f′为：

当x=lc时，z（x）取得最大值，此时的位置为三铰斜拱的拱顶位置，此时拱顶水平距离为：

联立式（11）和式（12），可得：

采空区顶板岩层破断高度、卸压区宽度、前后拱脚位置由三铰斜拱形态参数（拱顶水平距离lc、斜拱高f′、斜拱跨度l、斜拱倾角α 等）确定，而其形态参数与留设煤柱宽度、煤层开采高度、顶板岩性、采空区卸压宽度、开采过程等动态相关。

2 形态参数求解

2.1 数值模型

根据山西上良煤矿32306 工作面实际地层赋存条件建立FLAC3D数值模拟模型，模型尺寸为600 m×500 m×95 m（x×y×z），共有580 000 个单元格，601 859 个节点，x 方向为工作面开采倾向方向，y 方向为工作面走向方向，开采模型示意图如图4。模型顶部实际埋深约200 m，上方未模拟200 m 岩层，根据等效载荷公式，确定模型顶部采用5 MPa 的压力边界，底部采用固定边界，其余面均为滚支边界。煤层属近水平煤层，模型中作水平煤层处理，模型破坏准则选用Mohr-Coulomb 准则，结合山西上良煤矿地质报告，实验室力学测试数据，岩层物性参数见表1。

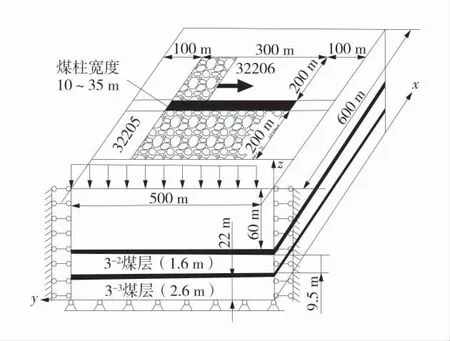
图4 开采模型示意图Fig.4 Schematic diagram of mining model

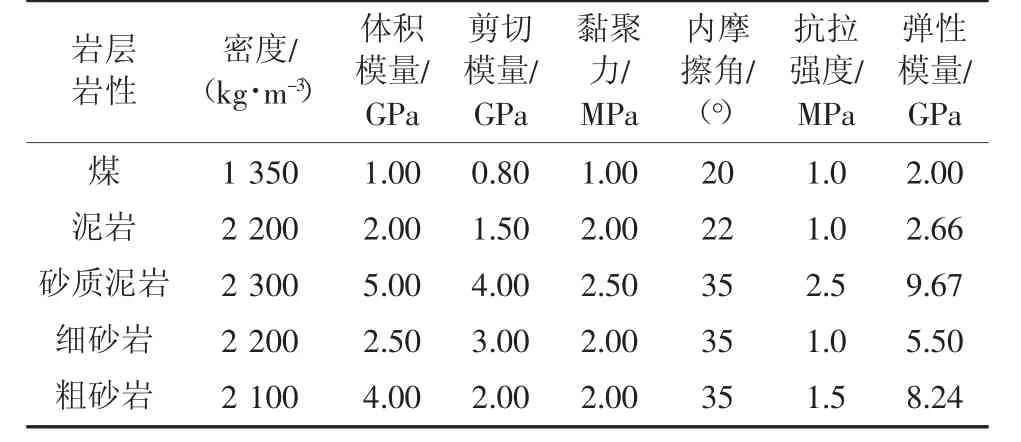
表1 煤岩层物性参数Table 1 Physical parameters of coal and rock

沿走向开采3-2#煤层，先开挖邻近32205 工作面，再开挖32206 工作面，2 个工作面的开挖尺寸均为300 m×200 m×2 m（x×y×z），工作面前后煤柱宽度为100 m。工作面左右煤柱宽度随留设保护煤柱宽度的不同而不同。模拟计算2 个工作面间的煤柱宽度分别为10、15、20、25、30、35 m 时开采后的三铰斜拱形态参数。形态参数包括：斜拱跨度l；煤柱弹性应力增高区宽度2t；煤柱塑性区宽度s；采空区卸压区宽度r；采空区应力恢复区宽度n；采空区压实区宽度m；拱顶水平距离lc；斜拱高f′；煤柱应力集中系数K；泊松比μ；三铰拱倾角α；采空区压实区应力集中系数β。基本参数取：H=260 m，ρ=2.5 t/m3，φ=38°。

2.2 结果分析

2.2.1 采空区底板竖向应力

模拟结果表明，3-2#煤层竖向原岩应力约为6 MPa。用Tecplot 软件对模拟结果进行后处理，导出区段保护煤柱宽度分别为10、15、20、25、30、35 m时的底板下方5 m 处垂直应力云图如图5。

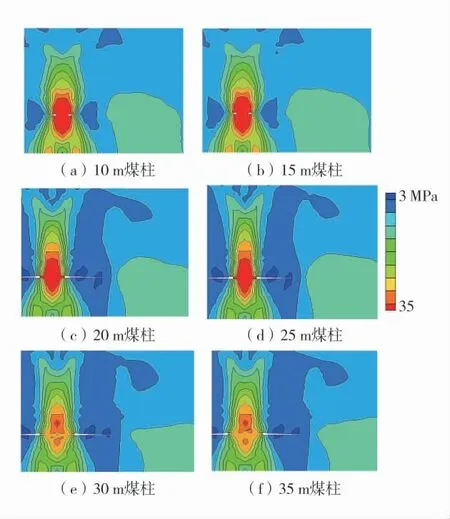
图5 不同煤柱宽度下垂直应力云图Fig.5 Vertical stress cloud diagrams under different pillar widths

由图5 可知，当工作面开采后，采空区底板垂直方向应力近似呈“O”形圈分布规律：采空区最外围为区段煤柱、边界煤柱、工作面前方煤岩影响下的卸压区；次外层为应力恢复区；中心范围为明显的原岩应力区，由于三角斜拱结构带来的附加应力影响，采空区最中心部分的应力大于原岩应力。

上保护层工作面充分采动后，上覆岩层载荷集中在两侧煤柱及采空区原岩应力恢复区，在煤柱正下方的底板岩层中出现集中应力影响区。沿工作面倾向，在保护层底板不同深度处以5 m 为间隔布置6 条测线，提取的煤柱正下方到采空区原岩应力恢复区不同深度处的竖向应力变化曲线如图6。

图6 不同宽度煤柱底板应力变化曲线Fig.6 Stress variation curves of coal pillar floor with different widths

由图6 可知：从煤柱正下方到采空区原岩应力恢复区可依次分为煤柱集中应力影响区、卸荷破坏影响区、原岩应力恢复区和重新压实区；当区段煤柱宽度为10 m 和15 m 时，沿工作面倾向底板埋深30 m 范围内，煤柱集中应力影响区长度大于煤柱宽度，这是由于此时煤柱应力集中程度过大导致；当区段煤柱宽度为20 m 和25 m 时，沿工作面倾向底板埋深30 m 范围内，煤柱集中应力影响区长度等于煤柱宽度，这说明此时煤柱应力集中程度适中；当区段煤柱宽度为30 m 和35 m 时，沿工作面倾向底板埋深30 m 范围内，煤柱集中应力影响区长度小于煤柱宽度，这是由于此时煤柱应力集中程度较小导致。

在煤柱集中应力影响区和原岩应力恢复区，都有一定程度的应力集中。煤柱宽度一定，随着埋深增加，应力集中程度减小，垂直应力与埋深呈负相关；在卸荷破坏影响区，没有应力集中影响，垂直应力随埋深增大而增大，垂直应力与埋深呈正相关。

2.2.2 形态参数分析

3-2#煤层底板下方5 m 煤层倾向应力变化曲线（局部放大）如图7。

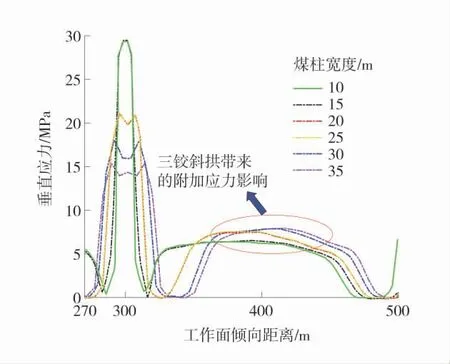
图7 煤层倾向应力变化曲线（局部放大）Fig.7 Variation curves of coal seam dip stress（local amplification）

由图7 可知：当留设保护煤柱宽度小于15 m时，此时煤柱受到完全塑性破坏，无法形成三铰斜拱的1 个拱脚支撑点，故不存在三铰斜拱的力学结构；当煤柱宽度大于15 m 时，煤柱内部出现稳定的弹性区，随着保护煤柱宽度的增加，煤柱中弹性应力区占比逐渐增加，煤柱承载能力增大，煤柱的稳定性增加，此时便可形成三铰斜拱的1 个拱脚支撑点。采空区底板应力极值随保护煤柱宽度增加而增加，是由于煤柱的承载能力增强，采空区底板卸压范围逐渐扩大，三铰斜拱的跨度也逐渐增加，三铰斜拱受到的载荷范围增大所致。

采空区上方三铰斜拱基本对称分布，故只分析区段保护煤柱到采空区重新压实区中心处。结合图8 得出的三铰斜拱的相关参数见表2。

表2 三铰斜拱形态参数Table 2 Shape parameters of three-hinged inclined arch

由表2 可知：随着保护煤柱宽度的增加，煤柱底板弹性区占比由40%增加到71%，最大应力集中系数由3.69 降低到2.30，煤柱的稳定性逐渐增加；同时，保护煤柱宽度增加导致卸压区范围增加，因此，三铰斜拱的跨度也随之增大。

3 采空区底板应力计算

3.1 三铰斜拱结构应力计算

由表2 中斜拱高度f′可知，直接顶垮落高度为6～8 m，基本顶断裂高度为26～31 m，结合图5 和表1，计算三铰斜拱上覆岩层载荷，此处计算时，将大厚度岩层考虑为多层岩层分开运动[22]，中间2#不可采煤层忽略不计。不同宽度煤柱下的三铰斜拱载荷分布见表3。

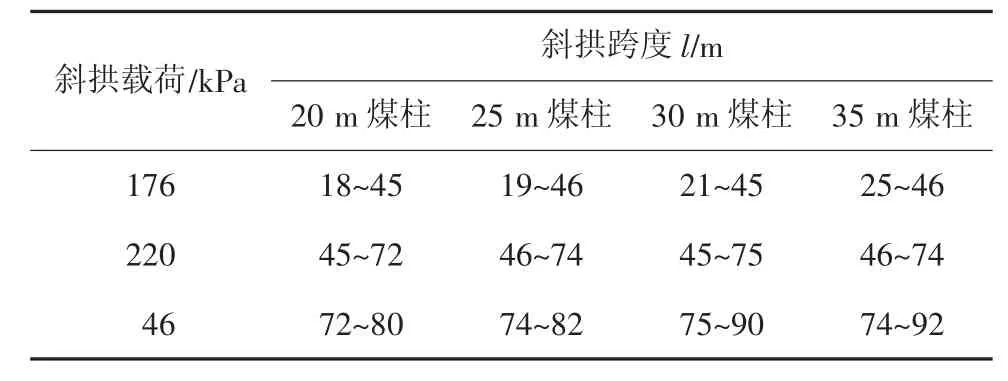
表3 不同煤柱下三铰斜拱载荷分布Table 3 Load distribution of three-hinged oblique arches under different coal pillars

由表3 可知：根据3-2#煤层的上覆岩层分布情况，不同的三铰斜拱跨度对应的岩性和上覆载荷不同，三铰斜拱扩展范围由3-2#煤层上方6 m 的细砂岩扩展到上方29 m 细砂岩底部。

由于采动影响，采空区底板应力将重新分布，采空区重新压实区应力将恢复到原岩应力。3-2#煤层充分采动后，由于遗留区段煤柱宽度不同，形成的三铰斜拱结构不同，采空区底板附加应力也不同。根据不同煤柱宽度下的形态参数，结合式（4）、式（5）可以计算煤层底板的水平应力和垂直应力。煤层底板垂直应力变化曲线图如图8。

图8 煤层底板垂直应力变化曲线图Fig.8 Curves of vertical stress change of coal seam floor

由图8 可知：通过三铰斜拱力学模型计算出的垂直应力在距离煤柱35 m 左右达到原岩应力；超过35 m 后，由于三铰斜拱产生的附加应力，重新压实区的垂直应力逐渐增加，最大达到约8 MPa。水平应力变化趋势与垂直应力基本一致，垂直大小约为垂直应力的35%倍，即通过三铰斜拱力学模型计算出的侧向应力系数λ=0.35。

3.2 弹性力学理论应力计算

为简化计算，将应力增高简化为线性增加，根据弹性力学理论，底板岩层相当于半无限体，各段附加载荷q 为：

塑性区AB 段：

弹性应力增高区BC 段：

弹性应力增高区CD 段：

塑性区DE 段：

卸压区EF 段：

应力恢复区FG 段：

重新压实区GJ 段：

将保护层工作面底板煤岩层视为均质弹性体，根据弹性力学理论[23]，集度为q（ξ）的面力作用在均质且各向同性的空间半无限平面边界上，整个分布载荷在底板中任意点M（x，y）所产生的应力值为：

式 中：σx为 水 平 应 力，MPa；σz为 垂 直 应 力，MPa；x，z 分别为集中力F 到M 点的垂直距离和水平距离，m。

将各个微小集中力所引起的应力相叠加，可得：

利用Mathcad 软件计算结果，得出不同煤柱宽度下的采空区一侧底板应力分布曲线，应力变化曲线图如图9。将2 种计算结果进行对比，研究表明：通过三铰斜拱力学模型计算得到的采空区沿工作面倾向分布的水平应力和垂直应力，在变化趋势方面，与通过弹性力学理论计算所得结果基本保持一致。在数值大小方面，煤柱宽度为20、25、30、35 m时的垂直应力平均误差为:9.20%、6.16%、9.61%、8.45%，水平应力平均误差为：12.33%、11.62%、8.71%、9.87%。

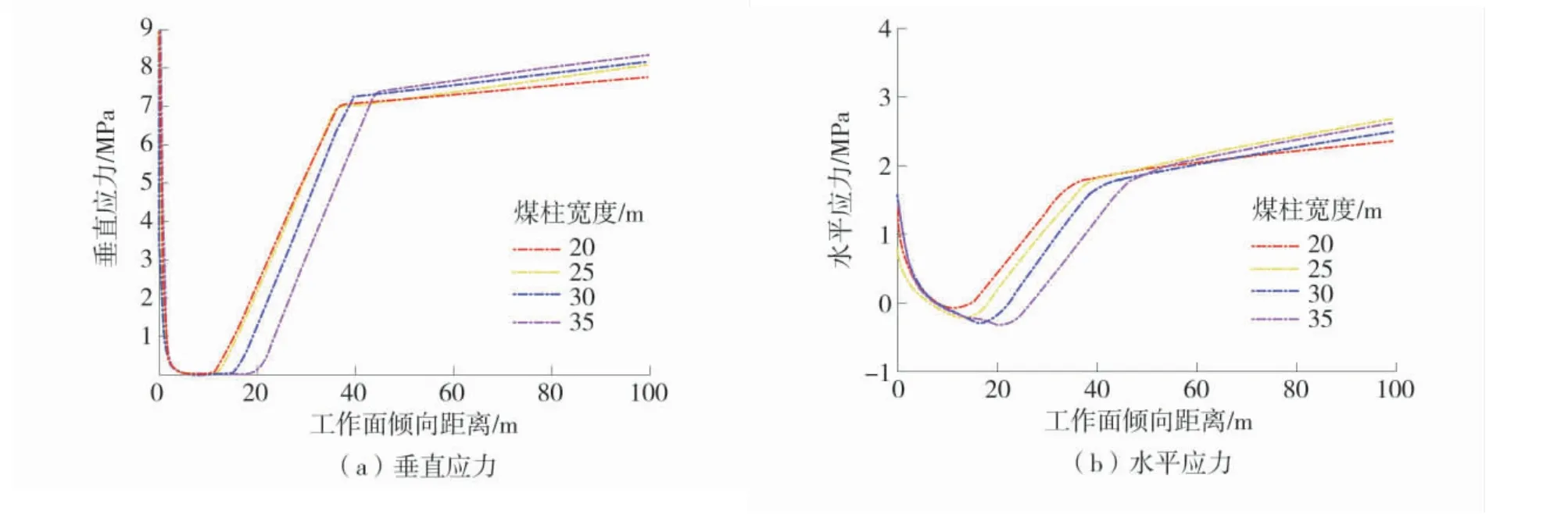
图9 采空区一侧底板应力变化曲线图Fig.9 Curves of stress change on the one side of goaf

基于三铰斜拱力学模型的计算结果相比偏大的原因为：采动岩层的载荷是非均匀分布的，但为了简化分析问题，假设三铰斜拱的上覆岩层载荷是均匀分布的。

4 现场实测

上良煤矿3-2#煤层32205、32206 工作面间的区段保护煤柱宽度为25 m，在32206 工作面回风巷施工下向钻孔。采用应力采集系统测量3-2#煤层32206工作面回采后地应力变化规律，同时通过深部基点法监测底板煤岩相对变形量。

现场布置钻孔，终孔在竖直方向位置为3-2#煤层采空区底板下方5 m 处，水平方向距离为距回风巷0～100 m 范围，底板应力及相对变形量变化曲线如图10。

图10 底板应力及相对变形量变化曲线Fig.10 Curves of stress and relative deformation of floor

由图10 可知：沿工作面倾向，在距离煤柱约为5 m 以内时，是煤柱的应力集中影响区，此处底板竖直应力较大，底板煤岩压缩变形；在距离为5～23 m区域，此时底板最大应力为1.4 MPa，未恢复到原岩应力，而且底板卸荷相对变形量达到最大为0.24%；在距离煤柱超过23 m 后，由于采空区逐渐压实，底板应力逐渐恢复，相对变形量也相应减小；而且在采空区中心处受三铰斜拱结构影响，产生了附加应力，底板应力达到最大值8.3 MPa，相对变形量也达到最小值0.75%。

将图10 中现场实测数据与图6（d）中对应的模拟结果对比，二者整体变化趋势一致；将现场实测数据与三铰斜拱和弹性力学理论的解析解进行误差分析得：垂直应力的平均误差分别为3.02%和9.18%，可见三铰斜拱理论可以更好地描述实际情况下底板的垂直应力变化。根据模拟结果与现场实测，综合考虑底板卸压效果，建议被保护层回采巷道在卸荷破坏区内错布置，错距为10～20 m。

5 结 语

1）上保护层充分采动后，采场空间的裂断拱内，在垮落带上方的规则移动带形成了三铰斜拱的力学结构，其中1 个拱脚的支撑点位于保护煤柱的弹性区，另1 个拱脚的支撑点位于采空区的应力恢复区和重新压实区。

2）当留设保护煤柱宽度小于15 m 时，此时煤柱内无弹性区，无法形成三铰斜拱的1 个拱脚支撑点。当煤柱宽度大于15 m 时，煤柱内部出现稳定的弹性区，此时可形成三铰斜拱的1 个拱脚支撑点，随着保护煤柱宽度增加，采空区卸压区范围增加，三铰斜拱的跨度也随之增大。

3）在煤柱集中应力影响区和原岩应力恢复内，煤柱宽度一定时，随着埋深增加，应力集中程度减小，垂直应力与埋深呈负相关；在卸荷破坏影响区内，垂直应力随埋深增大而增大，垂直应力与埋深呈正相关。

4）通过现场测定采空区底板应力及变形规律，发现在重新压实区存在附加应力。综合考虑底板卸压效果，建议被保护层回采巷道在卸荷破坏区内错布置，合理错距为10～20 m。